Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
Дана правильная шестиугольная пирамида SABCDEF с вершиной S.
а) Докажите, что плоскость, проходящая через середины рёбер SA и SD и вершину C, делит апофему грани ASB в отношении 2 : 1, считая от вершины S.
б) Найдите отношение, в котором плоскость, проходящая через середины рёбер SA и SD и вершину C, делит ребро SF, считая от вершины S.
Спрятать решение
Решение.
а) Обозначим за M, N середины ребер SA и SD. Поскольку MN — средняя линия треугольника SAD, то поэтому точка B также лежит в данной плоскости. Поэтому с гранью ABS данная плоскость пересекается по прямой BM — медиане треугольника SAB. Она делит его медиану SQ (Q — середина AB) в отношении 2 : 1 считая от вершины.
б) Пусть Поскольку MN — средняя линия треугольника SAD, она делит отрезок SK пополам, то есть T — середина SK. Ясно, что T лежит в данной плоскости.
Рассмотрим теперь треугольник SBF. В нем проведена медиана SK и отмечена ее середина T. В данной плоскости лежит прямая BT, пересекающая SF в точке W. Осталось выяснить местоположение точки W.
Напишем теорему Менелая для треугольника FSK и прямой откуда
Ответ: 1 : 2.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б)
ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки |
2 |
| Имеется верное доказательство утверждения пункта а)
ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен |
1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Александр Пьянков 10.02.2017 16:58
Можно поподробнее, откуда вы взяли, что точка В лежит в плоскости сечения?
Александр Иванов
из параллельности
Александр Митченко 24.04.2017 05:21
На мой взгляд, условие, состоящее в том, что боковое ребро вдвое больше ребра основания, не используется при решении задачи и является лишним.
Служба поддержки
Согласны, убрали из условия это уточнение.
Егэ математика профиль 513266
Задание 13 № 513266
Дана правильная шестиугольная пирамида SABCDEF с вершиной S.
А) Докажите, что плоскость, проходящая через середины рёбер SA и SD и вершину C, делит апофему грани ASB в отношении 2 : 1, считая от вершины S.
Б) Найдите отношение, в котором плоскость, проходящая через середины рёбер SA и SD и вершину C, делит ребро SF, считая от вершины S.
А) Обозначим за M, N середины ребер SA и SD. Поскольку MN — средняя линия треугольника SAD, то поэтому точка B также лежит в данной плоскости. Поэтому с гранью ABS данная плоскость пересекается по прямой BM — медиане треугольника SAB. Она делит его медиану SQ (Q — середина AB) в отношении 2 : 1 считая от вершины.
Б) Пусть Поскольку MN — средняя линия треугольника SAD, она делит отрезок SK пополам, то есть T — середина SK. Ясно, что T лежит в данной плоскости.
Рассмотрим теперь треугольник SBF. В нем проведена медиана SK и отмечена ее середина T. В данной плоскости лежит прямая BT, пересекающая SF в точке W. Осталось выяснить местоположение точки W.
Напишем теорему Менелая для треугольника FSK и прямой откуда
При обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Задание 13 № 513266
Рассмотрим теперь треугольник SBF.
Ege. sdamgia. ru
22.11.2019 19:33:29
2019-11-22 19:33:29
Источники:
Https://ege. sdamgia. ru/problem? id=513266
Егэ математика профиль 513266 — Математика и Английский » /> » /> .keyword { color: red; } Егэ математика профиль 513266
Егэ математика профиль 513266
Егэ математика профиль 513266
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 5 № 27113
Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды равен 1. Найдите объем шестиугольной пирамиды.
Данные пирамиды имеют общую высоту, поэтому их объемы соотносятся как площади их оснований. Площадь правильного шестиугольника со стороной A равна Площадь же равнобедренного треугольника ACB с боковой стороной A и углах при основании 30° равна Получаем, что площадь шестиугольника больше площади треугольника ACB в раз и равна 6.
Задание 5 № 27113
Егэ математика профиль 513266.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Егэ математика профиль 513266
Егэ математика профиль 513266
Егэ математика профиль 513266
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 13 № 484567
Дана правильная шестиугольная пирамида SABCDEF.
А) Докажите, что угол между прямыми SB и CD равен углу SBE.
Б) Если стороны основания равны 1, а боковые ребра равны 2, найдите угол между прямыми SB и CD.
А) Вместо прямой CD рассмотрим параллельную ей прямую BE. Искомый угол равен углу SBE.
Б) Треугольник SBE равносторонний, поскольку большая диагональ правильного шестиугольника вдвое больше его стороны: Следовательно,
При обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Задание 13 № 484567
Б Если стороны основания равны 1, а боковые ребра равны 2, найдите угол между прямыми SB и CD.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Егэ математика профиль 513266
Егэ математика профиль 513266
Егэ математика профиль 513266
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 13 № 513266
Дана правильная шестиугольная пирамида SABCDEF с вершиной S.
А) Докажите, что плоскость, проходящая через середины рёбер SA и SD и вершину C, делит апофему грани ASB в отношении 2 : 1, считая от вершины S.
Б) Найдите отношение, в котором плоскость, проходящая через середины рёбер SA и SD и вершину C, делит ребро SF, считая от вершины S.
А) Обозначим за M, N середины ребер SA и SD. Поскольку MN — средняя линия треугольника SAD, то поэтому точка B также лежит в данной плоскости. Поэтому с гранью ABS данная плоскость пересекается по прямой BM — медиане треугольника SAB. Она делит его медиану SQ (Q — середина AB) в отношении 2 : 1 считая от вершины.
Б) Пусть Поскольку MN — средняя линия треугольника SAD, она делит отрезок SK пополам, то есть T — середина SK. Ясно, что T лежит в данной плоскости.
Рассмотрим теперь треугольник SBF. В нем проведена медиана SK и отмечена ее середина T. В данной плоскости лежит прямая BT, пересекающая SF в точке W. Осталось выяснить местоположение точки W.
Напишем теорему Менелая для треугольника FSK и прямой откуда
При обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Егэ математика профиль 513266
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 13 № 484567
Дана правильная шестиугольная пирамида SABCDEF.
А) Докажите, что угол между прямыми SB и CD равен углу SBE.
Б) Если стороны основания равны 1, а боковые ребра равны 2, найдите угол между прямыми SB и CD.
А) Вместо прямой CD рассмотрим параллельную ей прямую BE. Искомый угол равен углу SBE.
Б) Треугольник SBE равносторонний, поскольку большая диагональ правильного шестиугольника вдвое больше его стороны: Следовательно,
При обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Задание 13 № 484567
Б Если стороны основания равны 1, а боковые ребра равны 2, найдите угол между прямыми SB и CD.
Напишем теорему Менелая для треугольника FSK и прямой откуда.
Dankonoy. com
18.12.2020 11:05:05
2020-12-18 11:05:05
Источники:
Https://dankonoy. com/ege/ege12/archives/1899
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Егэ математика профиль 513266
Егэ математика профиль 513266
Егэ математика профиль 513266
Задания Д9 C2 № 484576
В правильной шестиугольной призме стороны основания которой равны 4, а боковые ребра равны 3, найдите расстояние от точки В до прямой
Так как ABCDEF правильный шестиугольник, то прямые BE и CD параллельны, параллельны также прямые и CD, следовательно, прямые и BE параллельны. Расстояние от точки B до прямой равно расстоянию между прямыми и
Задания Д9 C2 № 484576
Задания Д9 C2 484576.
Reshuege. ru
23.07.2018 8:59:30
2018-07-23 08:59:30
Источники:
Https://reshuege. ru/problem? id=484576
ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также:

Задание №11 решу ЕГЭ 2022 по математике 11 класс профильный уровень (профиль) все задания с ответами и решением, которые могут попасться на реальном ЕГЭ 2022.
- Степенные иррациональные функции
- Логарифмические функции
- Показательные функции
- Тригонометрические функции
- Исследование функции без производной
Задание 11 часть 1 профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной. Вот какие типы задач могут встретиться в этом задании:
- Нахождение точек максимума и минимума функций
- Исследование сложных функций
- Нахождение наибольших и наименьших значений функций на отрезке
Степенные иррациональные функции ЕГЭ 2022 профиль математика:
Логарифмические функции ЕГЭ 2022 профиль математика:
Показательные функции ЕГЭ 2022 профиль математика:
Тригонометрические функции ЕГЭ 2022 профиль математика:
Исследование функции ЕГЭ 2022 профиль математика:
Видео как решать 11 задание в ЕГЭ по математике профиль:
1)Найдите наименьшее значение функции y=−2ln(x+3)5+10x на отрезке [−2,5;−1].
2)Найдите наибольшее значение функции y=ln(x+7)3−3x на отрезке [−6,5;−4].
3)Найдите наибольшее значение функции y=ln(4−2x)+2x−7 на отрезке [0;1,7].
4)Найдите точку максимума функции y=−8√x+12ln(x−4)−11.
5)Найдите точку максимума функции y=2lnx−√x−17.
6)Найдите наибольшее значение функции y=√−2log0,5(5x+1) на отрезке [12,6;51].
7)Найдите точку минимума функции y=x2−21x+6+55lnx.
8)Найдите точку максимума функции y=x2−11x−17+15lnx.
9)Найдите точку максимума функции y=(5×2−3x−3)ex+5.
10)Найдите наименьшее значение функции y=−4x−4cosx+5 на отрезке [−π;0].
Тренировочные варианты ЕГЭ 2022 по математике профиль 11 класс
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Условие задачи
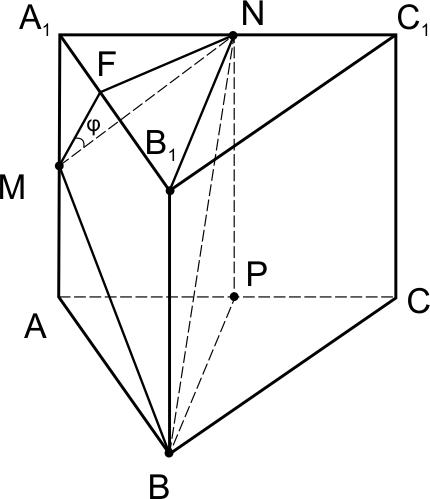
Все ребра правильной треугольной призмы имеют длину 6. Точки M и N – середины ребер
и
соответственно.
а) Докажите, что прямые ВМ и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и АВ B1.
Решение
а) Покажем, что ∠BMN=90°.
Пусть точка Р – середина АС.
В плоскости BNP проведем отрезок BN.
Рассмотрим треугольник BMN, из которого можно найти угол BMN.
Сначала найдём MN, BM и BN – стороны этого треугольника.
∆ABC правильный, ВР – его высота,
Из :
Из :
поскольку
Из :
Для треугольника BMN выполняется теорема Пифагора: Значит, он прямоугольный.
б) Найдем угол между плоскостями
и
Угол между плоскостями – это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.
Плоскости и
пересекаются по прямой ВМ, причем в пункте (а) мы доказали, что MN ⊥ BM. В плоскости
построим FM ⊥ BM.
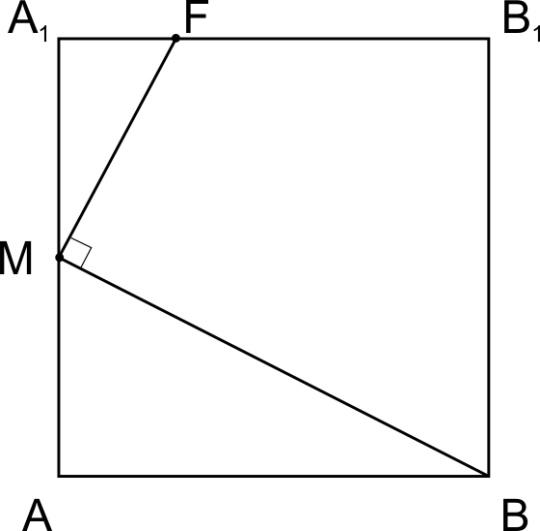
Заметим, что ,
, значит,
.
Отрезок NF равен половине высоты правильного треугольника ,
,
Кроме того, отрезок NF лежит в плоскости верхнего основания призмы, которая перпендикулярна боковому ребру .
Значит, .
Поскольку NF перпендикулярен двум пересекающимся прямым и
, лежащим в плоскости
, получим:
.
Тогда NF⊥FM; ∆NFM – прямоугольный,
Ответ:
б)
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Решение. Задание 14, Вариант 2» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-23

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!