Егэ математика профиль 2022 задание 9 презентация

Инфоурок

›

Алгебра

›Презентации›Презентация «Решение задания №9 ЕГЭ 2022»

Слайд 1

«ЗАДАНИЕ № 9 В ЕГЭ 2022 ПРОФИЛЬНОГО УРОВНЯ» Зялалова З.А учитель математики МБОУ ВСОШ №4

Слайд 2

Задание №9 . «Анализ графиков» Прямая Парабола Гипербола Логарифмическая и показательная функции Иррациональные функции Тригонометрические функции

Слайд 3

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1

Слайд 4

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:

Слайд 5

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:

Слайд 6

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:

Слайд 7

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:

Слайд 8

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:

Слайд 9

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:

Слайд 10

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:

Слайд 11

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение: Ответ: 4.

Слайд 12

По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2

Слайд 13

По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:

Слайд 14

По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:

Слайд 15

По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:

Слайд 16

По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:

Слайд 17

По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:

Слайд 18

По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:

Слайд 19

По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:

Слайд 20

По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:

Слайд 21

По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:

Слайд 22

По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:

Слайд 23

По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2 Решение:

Слайд 24

Прототип 1. (Прямая) На рисунке изображены графики двух линейных функций. Найдите ординату точек пересечения. 1 2 Решение: Уравнение прямой у = kx+b . 1) Первая прямая проходит через точки (-4;1) и (-2;4) , Решаем систему = > k=1,5; b=7 у =1,5х+7-уравнение 1 прямой. 2) Вторая прямая проходит через точки (-1;0) и (2;3) . Решаем систему = > k=1; b=1 Тогда у=х+1-уравнение 2 прямой. 3)Решим систему уравнений , х = -12.Тогда у = -11. Ответ:-11

Слайд 25

Прототип 2. (Парабола) На рисунке изображен график функции f(x)= x²+bx+c . Найдите f( -1 ) . Решение. Из рисунка видно, что график проходит через (3;2);(4;5);(5;4) В ычтем из 2 уравнения 1-е , п олучим7 a + b = Вычтем из 3уравнения 2 -е , получим 9 a + b=- Решив систему уравнений находим = -2 , b = 17. Тогда f(x )= — 2 x² + 17 x + c и f( 3 ) = 2, найдем ,что с = -31. f(x )= — 2 x²+ 17 x — 31, f( -1 ) =-2-17-31=-50 Ответ:-50

Слайд 26

Прототип 3 . (Парабола) На рисунке изображен график функции f(x)= ах ² + bx+c ,где числа , b и c -целые. Найдите абсциссу вершины параболы . Решение. Из рисунка видно, что график проходит через (3 ;-2);(2;1);(1;6) Тогда вычтем из 1 уравнения 2-е, получим 5a-b=- вычтем из 2 уравнения 3-е,получим 3 a-b=- Решив систему уравнений находим =1 , b =8. Абсцисса вершины параболы = — =-4 . Ответ:-4

Слайд 27

Прототип 4 . (Парабола) На рисунке изображены графики функций f(x )= 5х+9 и g(x)= ах ² + bx+c , которые пересекаются в точках А и В. Найдите абсциссу точки B Решение. По графику с=-3.График функции g(x) проходит через точки (-2;-1);(-1;-3);(2;3). Подставим координаты точки (-1;-3), получим -3=а- b -3. Отсюда а= b . g(x)= ах ² + а x -3. Подставим координаты точки (2;3 ), получим, что а=1. g(x)= х ² +x -3. Чтобы найти абсциссу точки ,нужно решить уравнение х ² +x -3 = 5х+9, х ² — 4 x — 12=0. По теореме Виета = -12, + = 4 По графику = -2, тогда =6. Ответ:6

Слайд 28

Прототип 5. (Гипербола) На рисунке изображен график функции f(x)= +a . Найдите f (0,25) Решение: График функции имеет горизонтальную асимптоту y = -2 , значит, а = -2 . ( График функции f(x ) = + a получается сдвигом графика функции f(x ) = вдоль оси Оу на величину |а| вверх, если а >0 и вниз если a<0 ) По графику а = -2 и проходит через точку (3;-3). -3 = -2 отсюда k = -3 .Значит, f(x ) = -2, f( 0,25 ) = -2= -14. Ответ:- 14

Слайд 29

Прототип 6 . (Гипербола) На рисунке изображён график функции вида f(x )= +c , где числа a, b и c — целые. Найдите f(13). Решение. График функции имеет горизонтальную асимптоту y = 2, значит, c = 2. График функции имеет вертикальную асимптоту x = 3 , значит, b = — 3. По графику f(2 ) = 1 , тогда +2=1, отсюда a = 1 . Таким образом, f(x ) = +2 Найдём f(13 ) = +2=2,1. f(13)=2,1. Ответ:2,1

Слайд 30

Прототип 7 . (Гипербола) На рисунке изображен график функции f(x)= . Найдите f . Решение. График функции имеет вертикальную асимптоту x = 2, значит, а = — 2. По графику а= -2 и проходит через точку (-3;-1). -1= , отсюда k = 5.Значит , f(x ) = , f = = 5: = -0,75. Ответ: -0,75

Слайд 31

Прототип 8. (Гипербола) На рисунке изображен график функции f(x)= . Найдите k Решение. Преобразуем данную функцию f(x)= f(x ) = Тогда, делаем вывод, что k- горизонтальная асимптота b -вертикальная асимптота График функции имеет горизонтальную асимптоту y=2, значит , k =2. Ответ:2

Слайд 32

Прототип 9 . (Гипербола) На рисунке изображен график функции f(x)= . Найдите a . Решение. График функции имеет горизонтальную асимптоту y=2, значит, k =2 . График функции имеет вертикальную асимптоту x=3, значит, b = — 3. По графику f( 5 )= 3, тогда 3= , отсюда а=-4. Ответ:-4 k-u горизонтальная асимптота b -вертикальная асимптота

Слайд 33

Прототип 10. ( Тригонометрическая функция ) На рисунке изображен график функции вида f(x )= cos(b π x+c )+d, где числа , b, c и d -целые. Найдите . Решение. По графику = -3 d = = = -1. |a|= = =2. По графику =2, c =0, T=2 T= = , то есть =2 , отсюда b=1 f (x)=2cos π x-1, f =f f , f =2cos π· -1 = 2cos π -1 = 2cos -1= -2cos 1= -2. Ответ:-2 Т=2

Слайд 34

Прототип 11.(Тригонометрическая функция) На рисунке изображён график функции вида f(x)= cos(b π x+c )+d, где числа , b, c и d -целые. Найдите . Решение. По графику = -3 d= = = -1. |a|= = =2. По графику = — 2 , c=0, T=2 T= = , то есть =2 , отсюда b=1 f(x )= — 2cos π x-1, f =f f , f = — 2cos π· -1 = — 2cos π -1 = — 2cos -1= 2cos 1= 0 . Ответ:0

Слайд 35

Прототип 12.(Иррациональная функция) На рисунке изображен график функции f(x)=k Найдите f(2,56) Решение. График этой функции проходит через точку (4;-3).Подставив координаты этой точки, получим -3= k , 2 k =-3, k =-1,5. f(2,56 ) =-1,5 Ответ:-2,4

Слайд 36

Прототип 13.(Логарифмическая функция) На рисунке изображен график функции f(x )=b+ x. Найдите значение х при котором f(x )=2. Решение. График функции f(x)= b+ x получается сдвигом графика функции f(x)= x. вдоль оси Оу на величину |b| вверх , если b > 0 и вниз если b <0 . По графику b = -2 и проходит через точку (3;- 1 ). -1= — 2 + , отсюда а =3 .Значит, f(x)= — 2 x , найдем х при котором f(x )= 2. 2=-2 x , x =4, значит, х=81. Ответ:81

Слайд 37

Прототип 14.(Показательная функция) На рисунке изображен график функции f(x )= . Найдите f (-5 ). Решение. График функции f(x)= получается сдвигом графика функции f(x)= вдоль оси Ох на величину | b | влево, если b>0 и вправо если b<0 . По графику b = — 1 и проходит через точку ( 3 ; 2 ). отсюда а = . Значит, f ( -5 )= = = Ответ:0,125

Решение задач №8,

ЕГЭ профиль.

Выполнила: Лаврова И.В.,

учитель МБОУ «Поташкинская СОШ»

15 км/ч через 1ч II 14 км/ч через 2ч III х км/ч III II I 14 15 30 III догонит I v = х – 15 = — =3 III догонит II v = x – 14 = — = 3 3 — 103 х + 840 =0 = 40/3 = 13 не удовл. ограничению = 21 Ответ: 21 » width=»640″

Задачи с тремя участниками движения. Статград 16.02.2022

Первый велосипедист выехал из посёлка по шоссе со скоростью 15 км/ч.

Через час после него со скоростью 14 км/ч из того же посёлка в том же

направлении выехал второй велосипедист, а ещё через час после этого —третий. Найдите

скорость третьего велосипедиста, если сначала он догнал второго, а через 3 часа после этого догнал первого. Ответ дайте в км/ч.

I 15 км/ч ограничения: v 15 км/ч

через 1ч II 14 км/ч

через 2ч III х км/ч

III II I

14 15 30

III догонит I v = х – 15 = — =3

III догонит II v = x – 14 =

— = 3

3 — 103 х + 840 =0

= 40/3 = 13 не удовл. ограничению = 21

Ответ: 21

Мультиурок учитель математики Лаврова Ирина Васильевна

Блог

Видео –задача с тремя участниками движения

Метод рычага

8. Смешав 38-процентный и 52-процентный растворы кислоты и добавив

10 кг чистой воды, получили 36-процентный раствор

кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 46-процентный раствор кислоты. Сколько килограммов 38-процентного раствора использовали для получения смеси?

38х + 52у = 36(х+у+10) (I)

38х+52у + 50∙10 = 46(х + у+ 10) (II)

10(х + у + 10) = 500

х + у + 10 = 50

х + у = 40 у=40-х, подставим в (1) х=20, у=20

Задачи на концентрацию и сплавы есть статьи :

Журналы «Математика в школе» №4, 94

«Математика в школе» №1, 97

Журнал «Математика . Всё для учителя» №2 [62] ст.Л.В.Гориной «Как перестать бояться и начать.. решать задачи на смеси и сплавы»,

стр.26

Журнал «Математика для школьников», №2, 2006,, С.Н.Олехник,

«Старинный способ решения задач на смешение веществ», стр. 56

Метод креста

12. Задание 8 №  99576

Имеется два сплава. Первый содержит 10% никеля, второй  — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

10% 5 частей

25%

30% 15 частей

• 15 +5 = 20(частей)-всего
• 200 : 20 = 10 г- масса 1 части
• 10 ∙5 = 50 (г) – масса 1 сплава
• 10 ∙ 15 = 150 (г) –масса 2 сплава
• 150- 50 =100 (г)
• Ответ : 100

Задание 8 №  99576

Имеется два сплава. Первый сплав содержит 10% меди, второй  — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

10% 10 частей

30%

40% 20 частей

• 20 – 10 = на 10 ( частей) больше масса 2 сплава
• 3 : 10 = 0,3 (кг) – в одной части
• 0,3 ∙10 = 3 (кг)- масса 1 сплава
• 0,3 ∙ 20 = 6 ( кг) – масса 2 сплава
• 3 + 6 = 9 (кг)

Ответ: 9 кг

№ 8. Курага получается в процессе сушки абрикосов. Сколько

килограммов абрикосов потребуется для получения 21 килограмма

кураги, если абрикосы содержат 86 % воды, а курага содержит 18 % воды?

%воды % сух. масса масса

вещ-ва сух.вещ-ва

абрикосы 86 14 % х 0,14х

курага 18 82 % 21 кг 0,82∙ 21

0,14х = 0,82 ∙ 21 14х = 82 ∙ 21

0,14х = 17,22 2х =82 ∙ 3

х = 123 х = 246 : 2

х = 123

Ответ: 123

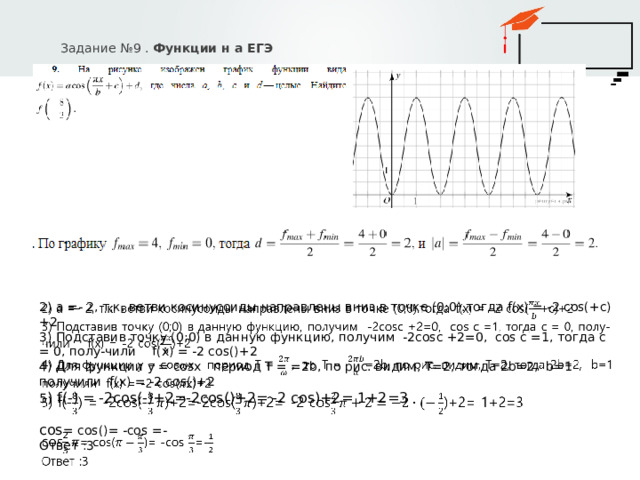
Задание №9 . Функции н а ЕГЭ

2) а =- 2, т.к. ветви косинусоиды направлены вниз в точке (0;0).тогда f(x) = -2 cos(+c)+2

3) Подставив точку (0;0) в данную функцию, получим -2cosc +2=0, сos c =1, тогда с = 0, полу-чили f(x) = -2 cos()+2

4) Для функции у = cosх период Т = =2b, по рис. видим, Т=2, тогда 2b=2, b=1

получили f(x) = -2 cos()+2

5 ) f(-) = -2cos(-)+2=-2cos()+2= -2 cos)+2= 1+2=3

cos = cos()= -cos =-

Ответ :3

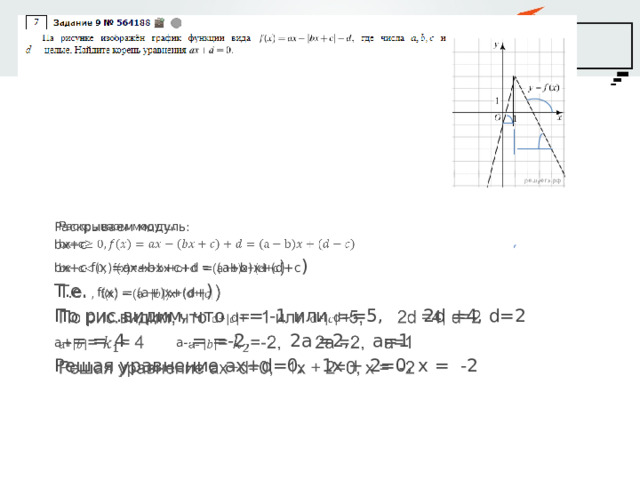
Раскрываем модуль:

bx+c

bx+c f(x)=ax+bx+c+d = (a+b)x+(d+c )

Т.е. f(x) = (a+)x+(d+ )

По рис.видим, что d+ = -1 или d+ =5, 2d =4, d=2

a+ = = 4 a- = =-2, 2a =2, a=1

Решая уравнение ax+d=0, 1x + 2=0, x = -2

Спасибо за внимание и понимание

1.

Задание 9 ЕГЭ- 2022
профильного
уровня по
математике
Графики функций
Рубцова Т.Г.
МБОУ Калманская СОШ имени Г.А. Ударцева, Алтайский край
2022 г.

2.

Кодификатор ЕГЭ 2022

3.

4.

Раздел 1
ЭЛЕМЕНТАРНЫЕ
ФУНКЦИИ И ИХ ГРАФИКИ

5.

Степенные функции

6.

Степенные функции

7.

Показательная и логарифмическая
функции

8.

Тригонометрические функции

9.

Обратные тригонометрические функции

10.

Раздел 2
ПРЕОБРАЗОВАНИЯ
ГРАФИКОВ ФУНКЦИЙ

11.

Сдвиг по горизонтали
Пусть функция задана формулой y = f(x) и a>0. Тогда график функции
y = f(x — m) сдвинут относительно исходного на m вправо. График
функции y = f(x + m) сдвинут относительно исходной на m влево.

12.

Сдвиг по вертикали
Пусть функция задана формулой y = f(x) и a>0 и С — некоторое
положительное число. Тогда график функции y = f(x)+n сдвинут
относительно исходного на n вверх. График функции y = f(x)-n сдвинут
относительно исходного на n вниз.

13.

Растяжение (сжатие) по горизонтали
Пусть функция задана формулой y = f(x) и k>0. Тогда график
функции y=(kx) растянут относительно исходного в k раз по
горизонтали, если 0<k<1, и сжат относительно исходного в k раз по
горизонтали, если k>1.

14.

Растяжение (сжатие) по вертикали
Пусть функция задана формулой y = f(x) и M>0. Тогда график
функции y = M∙f(x) растянут относительно исходного в М раз по
вертикали, если M>1 , и сжат относительно исходного в М раз по
вертикали, если 0<M<1.

15.

Отражение по горизонтали
График функции y = f(-x) симметричен графику функции y = f(x)
относительно оси Y.

16.

Отражение по вертикали
График функции y = -f(x) симметричен графику функции y = f(x)
относительно оси Х.

17.

Графики функций y = f(|x|) и y = |f(x)|

18.

Раздел 3
ВИДЫ ЗАДАЧ
И СПОСОБЫ ИХ РЕШЕНИЯ

19.

Виды задач
Используя предложенный график функции,
найти:
значения коэффициентов в уравнении функции;
абсциссу или ординату вершины параболы;
значение функции по данному значению
аргумента или значение аргумента по
заданному значению функции;
абсциссу или ординату точки пересечения
графиков функций;
значение дискриминанта квадратного
уравнения f(x)=т;
корень уравнения ax+d=0 или bx+c=0 (для
кусочно-линейных функций).

20.

Способы решения:
1) Нахождение коэффициентов функции через
решение систем уравнений, используя
целочисленные координаты точек графика ( в том
числе и точек пересечения с осями).
2) Нахождение коэффициентов, используя
вспомогательные формулы. Например, формулу
тангенса угла наклона прямой, абсциссы вершины
параболы, периодичности функции и др.)
3) Преобразование формулы, задающую функцию.
4) Нахождение коэффициентов через
преобразования графиков функций.

21.

1 способ

22.

23.

24.

25.

26.

27.

28.

2 способ

29.

30.

3 способ

31.

32.

4 способ

33.

34.

35.

36.

37.

38.

39.

Кусочно-линейная функция

40.

41.

42.

ИСПОЛЬЗУЕМЫЕ
ИНТЕРНЕТ-РЕСУРСЫ
https://ege-study.ru/ru/ege/materialy/matematika/elementarnyefunkcii-i-ix-grafiki/
https://ege-study.ru/preobrazovanie-grafikov-funkcij/
https://ege-study.ru/ru/ege/podgotovka/matematika/zadanie-9-egepo-matematike-grafiki-funkcij/
https://ege.sdamgia.ru/test?theme=191
https://unikum.rudn.ru/blog/printsipy-resheniya-zadachi-9-ege-pomatematike-2022
https://zen.yandex.ru/media/shevkin/kusochnolineinaia-funkciiazadanie-9-v-ege2022-61894df122ed344ee28e551d