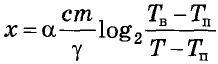Задание 15
Алексей планирует 15 декабря взять в банке кредит на 2 года в размере 1 806 000 рублей. Сотрудник банка предложил Алексею два различных варианта погашения кредита, описание которых приведено в таблице.
Вариант 1
— каждый январь долг возрастает на 15 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— кредит должен быть полностью погашен за два года двумя равными платежами
Вариант 2
— 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 24-го месяца кредит должен быть полностью погашен
На сколько рублей меньше окажется общая сумма выплат банку по более выгодному для Алексея варианту погашения кредита?
Ответ: 35 700 рублей
Скрыть
Пусть S — размер кредита, он равен 1806 тысячам рублей. Срок погашения кредита n составляет 2 года или 24 месяца. Процентная ставка r составляет в первом варианте 15% годовых, а во втором 2% ежемесячно.
В первом варианте долг х выплачен двумя платежами, поэтому $$(Scdot1,15-x)1,15-x=0$$,
откуда $$Scdot1,3225-2,15x=0Leftrightarrowfrac{Scdot1,3225}{2,15}Leftrightarrow x=frac{1806cdot1,3225}{2,15}=1110,9$$ тыс. руб.
Сумма выплат составляет:
$$1110,9cdot2=2221,8$$ тыс. руб.
Во втором варианте суммы долга составляют арифметическую прогрессию:
$$Scdot1,02, Scdot1,02cdotfrac{23}{24}, Scdot1,02cdotfrac{22}{24},cdots,Scdot1,02cdotfrac{1}{24}$$.
а выплаты равны:
$$Scdot0,02+frac{S}{24},frac{Scdot0,02cdot23+S}{24},frac{Scdot0,002cdot22+5}{24},cdots,frac{Scdot0,02+S}{24}$$.
Поэтому для суммы выплат получаем:
$$S+Scdot0,02(1+frac{23}{24}+frac{22}{24}+…+frac{1}{24})=S+Scdot0,02(frac{1+frac{1}{24}}{2}cdot24)=$$
$$=S+Scdot0,02cdotfrac{25}{2}=S+frac{S}{4}=1,25S$$ или $$1,25cdot1806=2257,5$$ тыс. руб.
Следовательно, более выгоден кредит, описанный в варианте 1; разность сумм выплат составит
$$2257,5-2221,8=35,7(тыс. руб.)=35700$$ руб.
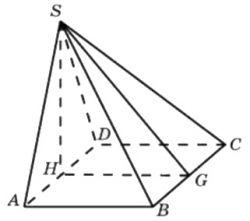
| 3235 | В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно sqrt21. На рёбрах AB и SB отмечены точки M и K соответственно, причём AM=4, SK:KB=1:3. а) Докажите, что плоскость CKM перпендикулярна плоскости ABC. б) Найдите объём пирамиды BCKM |
В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно корень из 21 ! 36 вариантов ФИПИ Ященко 2022 Вариант 13 Задание 13 | |
| 3205 | а) Решите уравнение (x^2+2x+1). (log_{2}(x^2-3)+log_{0.5}(sqrt(3)-x))=0. б) Найдите все корни этого уравнения, принадлежащие отрезку [-2,5; -1,5] |
Решите уравнение (x2 + 2x +1)(log2 (x2 -3)+ log0,5 (корень из 3 — x) ) =0 ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 13 Задание 12 # у Ященко ощибка в ответе пособия color{red}{ (a) -1-sqrt2; -1-sqrt3;} бcolor{red}{(б) -1-sqrt2} # Задача- аналог 2532 | |
| 3191 | Агрофирма закупает куриные яйца в двух домашних хозяйствах. 95% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 45% яиц высшей категории. Всего высшую категорию получает 60% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства |
Агрофирма закупает куриные яйца в двух домашних хозяйствах ! 36 вариантов ФИПИ Ященко 2022 Вариант 13 Задание 10 # Приведенорешениепрототипаcolor{blue} text{Приведено решение прототипа 1466}задачи- аналога 1466 | |
| 2533 | Имеется два сплава. Первый содержит 50% никеля, второй — 15 % никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго? |
Имеется два сплава. Первый содержит 50% никеля, второй — 15 % никеля ! 36 вариантов ФИПИ Ященко 2022 Вариант 13 Задание 8 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 3 Задание 11 | |
| 2531 | Решите неравенство (4^(x-0.5)+1)/(9*4^x-16^(x+0.5)-2) <= 0.5 |
Решите неравенство (4^(x-0,5)+ 1)/ (9*4^x-16^(x+0,5) -2) <= 0,5 ! 36 вариантов ФИПИ Ященко 2022 Вариант 13 Задание 14 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 3 Задание 15 | |
| 2530 | В четырёхугольнике ABCD противоположные стороны не параллельны. Диагонали четырёхугольника ABCD пересекаются в точке O под прямым углом и образуют четыре подобных треугольника, у каждого из которых одна из вершин — точка O. а) Докажите, что около четырёхугольника ABCD можно описать окружность. б) Найдите радиус вписанной окружности, если AC=10, BD=26 |
В четырёхугольнике ABCD противоположные стороны не параллельны ! 36 вариантов ФИПИ Ященко 2022 Вариант 13 Задание 16 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 3 Задание 16 | |
Решение и ответы заданий Варианта №13 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ профиль для 11 класса. Полный разбор.
Задание 1.
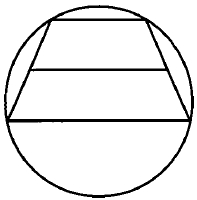
Около трапеции описана окружность. Периметр трапеции равен 38, средняя линия равна 11. Найдите боковую сторону трапеции.
Задание 2.
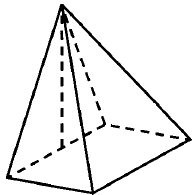
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объём пирамиды.
Задание 3.
На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной и меньше 7?
Задание 4.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,25. Вероятность того, что кофе закончится в обоих автоматах, равна 0,1. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Задание 5.
Решите уравнение x=frac{8x+36}{x+13}. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Задание 6.
Найдите значение выражения 24√10–3·21–3√10:2√10–1.
Задание 7.
Материальная точка движется прямолинейно по закону
x(t) = –frac{1}{3}t3 + 4t2 – 3t + 15,
где х – расстояние от точки отсчёта в метрах, t – время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени t = 7 с.
Задание 8.
Для обогрева помещения, температура в котором поддерживается на уровне Тп = 20 °C, через радиатор отопления пропускают горячую воду. Расход проходящей через трубу радиатора воды m = 0,5 кг/с. Проходя по трубе расстояние х, вода охлаждается от начальной температуры Тв = 72 °C до температуры Т, причём
где с = 4200 Вт·с/кг·°C – теплоёмкость воды, γ = 63 Вт/м·°C – коэффициент теплообмена, а α = 1,5 – постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 100 м.
Задание 9.
Имеется два сплава. Первый сплав содержит 5 % меди, второй – 14 % меди. Масса второго сплава больше массы первого на 5 кг. Из этих двух сплавов получили третий сплав, содержащий 12 % меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Задание 10.
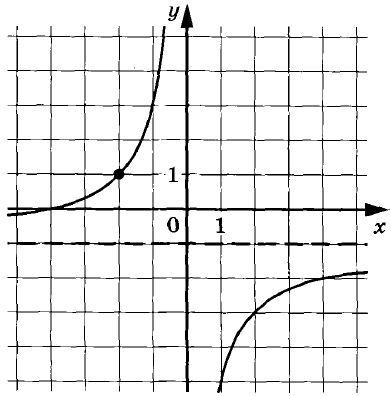
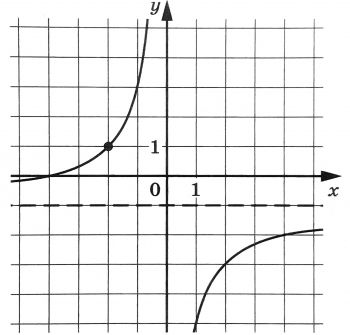
На рисунке изображён график функции f(х) = frac{k}{x} + а. Найдите f(–8).
Задание 11.
Найдите наименьшее значение функции y = 42cosx – 45x + 35 на отрезке [-frac{3pi}{2}; 0].
Задание 12.
а) Решите уравнение 3·9x+1 – 5·6x+1 + 4x+1,5 = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-frac{pi}{2};frac{pi}{2}].
Задание 13.
В правильной треугольной призме АВСА1В1С1 на рёбрах АС и ВС отмечены соответственно точки М и N так, что AM:МС = CN:BN = 2:1.
а) Докажите, что плоскость MNB1 проходит через середину ребра A1C1.
б) Найдите площадь сечения призмы АВСА1В1С1 плоскостью MNB1, если АВ = 6, АA1 = √3.
Задание 14.
Решите неравенство 27lg(x – 1) ≤ (х2 – 1)lg3.
Задание 15.
По вкладу «А» банк в конце каждого года увеличивает на 20 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивает эту сумму на 12 % в течение каждого из первых двух лет. Найдите наибольшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет менее выгоден, чем вклад «А».
Задание 16.
В параллелограмме ABCD угол А острый. На продолжениях сторон AD и CD за точку D выбраны точки М и N соответственно, причём AN = AD и CM = CD.
а) Докажите, что BN = BM.
б) Найдите MN, если АС = 5, sin∠BAD = frac{5}{13}.
Задание 17.
Найдите все положительные значения а, при каждом из которых корни уравнения 3а2х – 16х + 2·(4а)x = 0 принадлежат отрезку [–2; –1].
Задание 18.
Известно, что а, b, с, d, е и f – это различные, расставленные в некотором, возможно ином, порядке числа 2, 3, 4, 5, 6 и 16.
а) Может ли выполняться равенство frac{a}{b}+frac{c}{d}+frac{e}{f}=6?
б) Может ли выполняться равенство frac{a}{b}+frac{c}{d}+frac{e}{f}=frac{961}{240}?
в) Какое наименьшее значение может принимать сумма frac{a}{b}+frac{c}{d}+frac{e}{f}?
Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- ЕГЭ по математике профиль
Решение нового задания № 10 ЕГЭ 2022 по профильной математике из сборника Ященко.
На занятии рассмотрены некоторые задачи по теории вероятности из сборника с типовыми вариантами для подготовки к профильному ЕГЭ по математике 2022 под редакцией И.В. Ященко. Видео рекомендовано тем, кто владеет базовыми понятиями теории вероятности.
Видео представил YouTube канал Matesha Plus
→ Задание 10 ЕГЭ 2022 математика профильный уровень — практика
Купить ЕГЭ 2022 Математика. Профильный уровень. Типовые экзаменационные варианты. 36 вариантов
Для успешного выполнения задания 10 необходимо уметь моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий.
Связанные страницы:
Около трапеции описана окружность. Периметр трапеции равен 38, средняя линия равна 11. Найдите боковую сторону трапеции.
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объём пирамиды.
На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной и меньше 7?
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,25. Вероятность того, что кофе закончится в обоих автоматах, равна 0,1. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решите уравнение (x=dfrac{8x+36}{x+13}). Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Найдите значение выражения (2^{4sqrt{10}-3}cdot 2^{1-3sqrt{10}}:2^{sqrt{10}-1})
Материальная точка движется прямолинейно по закону (x(t)=-dfrac{1}{3}t^3+4t^2-3t+15), где (x) — расстояние от точки отсчёта в метрах, (t) — время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени (t=7, с)
Для обогрева помещения, температура в котором поддерживается на уровне (T_п=20 °C), через радиатор отопления пропускают горячую воду. Расход проходящей через трубу радиатора воды (m=0{,}5, кг/с). Проходя по трубе расстояние (x), вода охлаждается от начальной температуры (T_в=72 °C) до температуры (T), причём (x=alphadfrac{cm}{γ}log_{2}{frac{T_в-T_п}{T-T_п}}), где (c=4200,dfrac{Втcdot с}{кгcdot °C}) — теплоёмкость воды, (γ=63,dfrac{Вт}{мcdot °C}) — коэффициент теплообмена, а (alpha=1{,}5) — постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 100 м.
Имеется два сплава. Первый сплав содержит 5% меди, второй – 14% меди. Масса второго сплава больше массы первого на 5кг. Из этих двух сплавов получили третий сплав, содержащий 12% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
На рисунке изображен график функции (f(x)=dfrac{k}{x}+a). Найдите (f(-8)).
Найдите наименьшее значение функции ( y=42cos{x}-45x+35) на отрезке (left[-dfrac{3pi}{2};0right])
а) Решите уравнение ( 3cdot9^{x+1}-5cdot6^{x+1}+4^{x+1,5}=0 ).
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[-dfrac{pi}{2};dfrac{pi}{2}right]).
В ответ запишите корни без пробелов через точку с запятой в порядке возрастания. Сначала на пункт А, затем на пункт Б. Например, «8;13;8»
В правильной треугольной призме (ABCA_1B_1C_1) на рёбрах (AC) и (BC) отмечены соответственно точки (M) и (N) так, что (AM : MC = CN : BN = 2:1).
а) Докажите, что плоскость (MNB_1) проходит через середину ребра (A_1C_1).
б) Найдите площадь сечения призмы (ABCA_1B_1C_1) плоскостью (MNB_1), если (AB=6), (AA_1=sqrt{3}).
Решите неравенство (27^{lg{(x-1)}}leqslant (x^2-1)^{lg3})
По вкладу «А» банк в конце каждого года увеличивает на 20% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает эту сумму на 12% в течение каждого из первых двух лет. Найдите наибольшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет менее выгоден, чем вклад «А».
В параллелограме ABCD угол A острый. На продолжениях сторон AD и CD за точку D выбраны точки M и N соответственно, причём AN=AD и CM=CD.
а) Докажите, что BN=BM.
б) Найдите MN, если AC=5, sin∠BAD=5/13
Найдите все положительные значения (a), при каждом из которых корни уравнения (3a^{2x}-16^x+2cdot(4a)^x=0) принадлежат отрезку (left[-2;-1right]).
Известно, что (a), (b), (c), (d), (e) и (f) — это различные, расставленные в некотором, возможно ином, порядке числа 2, 3, 4, 5, 6 и 16.
а) Может ли выполняться равенство ( dfrac{a}{b}+dfrac{c}{d}+dfrac{e}{f}=6 )?
б) Может ли выполняться равенство ( dfrac{a}{b}+dfrac{c}{d}+dfrac{e}{f}=dfrac{961}{240} )?
в) Какое наименьшее значение может принимать сумма ( dfrac{a}{b}+dfrac{c}{d}+dfrac{e}{f} )?
Введите ответ в форме строки «да;да;12:34». Где ответы на пункты разделены «;», первые два ответа с маленькой буквы, в третьем несократимая дробь через двоеточие «:»
Всё варианты 13 задания математика ЕГЭ Профиль 2022
Скачать задания в формате pdf.
Задания 13 ЕГЭ по математике профильного уровня 2022 год (стереометрия)
1) (28.03.2022 досрочная волна) Вне плоскости равностороннего треугольника АВС отмечена точка D, причем (cos angle DAB = cos angle DAC = 0,2.)
а) Докажите, что прямые AD и ВС перпендикулярны
б) Найдите расстояние между прямыми AD и ВС, если известно, что АВ = 2.
ОТВЕТ: (frac{{sqrt {71} }}{5}.)
2) (28.03.2022 досрочная волна) Дана треугольная пирамида SABC. Основание высоты SO этой пирамиды является серединой отрезка CH — высоты треугольника ABC.
а) Докажите, что (A{C^2} — B{C^2} = A{S^2} — B{S^2};)
б) Найдите объём пирамиды SABC, если AB = 25; AC = 10; (BC = 5sqrt {13} ;,,,,SC = 3sqrt {10} .)
3) (28.03.2022 досрочная волна) На окружности основания конуса с вершиной S отмечены точки A, B и C так, что AB — диаметр основания. Угол между образующей и плоскостью основания равен 60°.
a) Докажите, что (cos angle ASC + cos angle CSB = 1,5;)
б) Найдите объём тетраэдра SABC, если SC = 1 и (cos angle ASC = frac{2}{3}.)
ОТВЕТ: (frac{{sqrt 6 }}{{36}}.)
4) (02.06.2022 основная волна) Дана правильная четырёхугольная пирамида SABCD. Точка M?— середина SA, на ребре SB отмечена точка N так, что SN : NB = 1 : 2.
а) Докажите, что плоскость CMN параллельна прямой SD.
б) Найдите площадь сечения пирамиды плоскостью CMN, если все рёбра равны 12.
ОТВЕТ: (15sqrt {19} .)
5) (02.06.2022 основная волна) В основании пирамиды SABCD лежит трапеция ABCD с большим основанием AD. Диагонали пересекаются в точке O. Точки M и N — середины боковых сторон AB и CD соответственно. Плоскость α проходит через точки M и N параллельно прямой SO.
а) Докажите, что сечение пирамиды SABCD плоскостью α является трапецией.
б) Найдите площадь сечения пирамиды SABCD плоскостью α, если SO = 9, AD = 12, BC = 10, а прямая SO перпендикулярна прямой AD.
6) (02.06.2022 основная волна) В прямоугольном параллелепипеде ABCDA1B1C1D1 на диагонали BD1 отмечена точка N так, что BN : ND1 = 1 : 2. Точка O — середина отрезка CB1.
а) Докажите, что прямая NO проходит через точку A.
б) Найдите объём параллелепипеда ABCDA1B1C1D1, если длина отрезка NO равна расстоянию между прямыми BD1 и CB1 и равна (sqrt 2 .)
7) (02.06.2022 основная волна) В кубе ABCDA1B1C1D1 отмечены середины M и N отрезков AB и AD соответственно.
а) Докажите, что прямые B1N и CM перпендикулярны.
б) Найдите расстояние между этими прямыми, если ({B_1}N = 3sqrt 5 .)

а) Докажите, что SK : KC = 6 : 1.
а) Плоскость AMN делит пирамиду SABCD на два многогранника. Найдите отношение их объёмов.
9) (02.06.2022 основная волна) В прямоугольном параллелепипеде ABCDA1B1C1D1 на диагонали BD1 отмечена точка N, что BN : ND1 = 1 : 2. Точка О – середина отрезка CB1.
а) Докажите, что прямая NО проходит через точку А.
б) Найдите объём параллелепипеда ABCDA1B1C1D1, если длина отрезка NO равна расстоянию между прямыми BD1 и CB1 и равна (sqrt 6 .)
10) (02.06.2022 основная волна) В правильной четырёхугольной пирамиде SABCD точка М – середина бокового ребра SC, точка N лежит на стороне основания BC. Плоскость α проходит через точки M и N параллельно боковому ребру SA.
а) Плоскость α пересекает ребро SD в точке L. Докажите, что BN : NC = DL : LS.
б) Пусть BN : NC = 1 : 2. Найдите отношение объёмов многогранников, на которые плоскость α разбивает пирамиду.
11) (02.06.2022 основная волна) Точка O?— точка пересечения диагоналей грани CDD1C1 куба ABCDA1B1C1D1. Плоскость DA1C1 пересекает диагональ BD1 в точке F.
а) Докажите, что BF : FD1 = A1F : FO.
б) Точки M и N — середины ребер AB и AA1, соответственно. Найдите угол между прямой MN и плоскостью DA1C1.
ОТВЕТ: (arctg,sqrt 2 .)
12) (27.06.2022 резервная волна) Точка М – середина ребра АА1 треугольной призмы АВСА1В1С1, в основании которой лежит треугольник АВС. Плоскость α проходит через точки В и В1 перпендикулярно прямой С1М.
а) Докажите, что одна из диагоналей грани АСС1А1 равна одному из рёбер этой грани.
б) Найдите расстояние от точки С до плоскости α, если она делит ребро АС в отношении 1 : 5, считая от вершины А и известно, что АС = 20, АА1 = 32.
13) (27.06.2022 резервная волна) В правильной треугольной призме ABCA1B1C1 точка М – середина ребра СС1. На рёбрах АВ и А1В1 взяты точки К и N так, что АК : КВ = В1N : NA1.
а) Докажите, что плоскость MKN перпендикулярна плоскости АА1В1.
б) Найдите площадь сечения призмы плоскостью MKN, если АВ = ВВ1 = 42 и ВК : КА = 41 : 1.
Варианты Ященко (ЕГЭ профиль): разбор в видеоформате
На данной странице представлены ссылки на видеоразборы всех 36 вариантов из сборника Ященко 2019 года.
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
31
32
33
34
35
36