Skip Navigation Links > Математика > ЕГЭ по математике 2022 > Математика 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко > Вариант 10 ( из 36 вариантов заданий ЕГЭ 2022 ФИПИ Ященко)

Кол-во задач: 2[1]
|
|
|
|||||||
|
|
|
|
| 3175 | В правильной треугольной призме ABCA1B1C1 точки K и N — соответственно середины рёбер AA1 и AC. Плоскость alpha проходит через точки K и N параллельно прямой CB1. а) Докажите, что сечением призмы ABCA1B1C1 плоскостью alpha является равнобедренная трапеция. б) Найдите угол между прямой CC1 и плоскостью alpha, если AB=4, AA1=sqrt3 |
В правильной треугольной призме ABCA1B1C1 точки K и N — соответственно середины рёбер AA1 и AC ! 36 вариантов ФИПИ Ященко 2022 Вариант 10 Задание 13 | |
| 3174 | Точка K лежит на отрезке AB. Прямая, проходящая через точку B, касается окружности с диаметром AK в точке N и второй раз пересекает окружность с диаметром BK в точке M. Продолжение отрезка NK пересекает окружность с диаметром BK в точке P. а) Докажите, что прямые AN и BP параллельны. б) Найдите площадь треугольника AKP, если BM=1 и MN=4 |
Точка K лежит на отрезке AB. Прямая, проходящая через точку B, касается окружности с диаметром AK в точке N и второй раз пересекает окружность! 36 вариантов ФИПИ Ященко 2022 Вариант 10 Задание 16 | |
Показана страница 1 из 1
| Clear |
Варианты Ященко (ЕГЭ профиль): разбор в видеоформате
На данной странице представлены ссылки на видеоразборы всех 36 вариантов из сборника Ященко 2019 года.
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
31
32
33
34
35
36
Основания равнобедренной трапеции равны 45 и 14. Высота трапеции равна 9,3. Найдите тангенс острого угла.
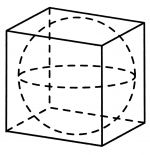
Прямоугольный параллелепипед описан около сферы радиуса 2,5. Найдите площадь его поверхности.
Рассмотрим случайный телефонный номер. Какова вероятность того, что среди трёх последних цифр этого номера хотя бы две цифры одинаковы?
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,34. Шахматисты А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Найдите корень уравнения (sqrt{dfrac{50}{5x+45}}=1dfrac14)
Найдите значение выражения (2^{12log_85})
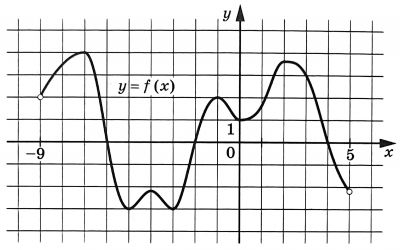
На рисунке изображен график функции y=f(x), определенной на интервале (-9;5). Найдите сумму точек экстремума функции f(x).
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 217 МГц. Скорость погружения батискафа (v) вычисляется по формуле (v=ccdotdfrac{f-f_0}{f+f_0}), где (c=1500) м/с – скорость звука в воде, (f_0) – частота испускаемых импульсов, (f) – частота отраженного от дна сигнала, регистрируемая приемником (в МГц). Определите частоту отраженного сигнала в МГц, если скорость погружения батискафа равна 12 м/с.
Боря и Ваня могут покрасить забор за 10 часов. Ваня и Гриша могут покрасить этот же забор за 15 часов, а Гриша и Боря – за 18 часов. За сколько часов мальчики покрасят забор, работая втроём?
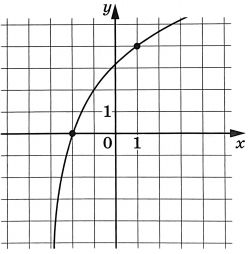
На рисунке изображен график функции (f(x)=log_a(x+3)). Найдите значение (x), при котором (f(x)=16)
Найдите наименьшее значение функци (y=e^{2x}-9e^x-3) на отрезке [0;3].
а) Решите уравнение (2sin xcdotsin2x=2cos x+cos2x)
б) Укажите все корни этого уравнения, принадлежащие отрезку (left[-dfrac{5pi}{2};-piright])
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4.π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -5π/2 | 18. -7π/3 | 19. -9π/4 | 20. -13π/6 |
| 21. -2π | 22. -11π/6 | 23. -7π/4 | 24. -5π/3 |
| 25. -3π/2 | 26. -4π/3 | 27. -5π/4 | 28. -7π/6 |
| 29. -π |
Грань ABCD прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ является вписанной в основание конуса, а сечением конуса плоскостью A₁B₁C₁ является круг, вписанный в четырехугольник A₁B₁C₁D₁; AB=a, AA₁=√2a.
а) Высота конуса равна h. Докажите, что 4,5a< h< 5a.
б) Найдите угол между плоскостями ABC и SD₁C, где S – вершина конуса.
Решите неравенство (log_5x^2+4log_{25}(6-2x)geqslantlog_{sqrt5}(x^2-4)+2log_{0{,}2}(2-x))
В июле Анна планирует взять кредит на 3 года на целое число миллионов рублей. Два банка предложили Анне оформить кредит на следующих условиях:
– в январе каждого года действия кредита долг увеличивается на некоторое число процентов (ставка плавающая – может быть разным для разных годов);
– в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью.
В первом банке процентная ставка по годам составляет 10, 20 и 15 процентов соответственно, а во втором – 15, 10 и 20 процентов. Анна выбрала наиболее выгодное предложение. Найдите сумму кредита, если эта выгода по общим выплатам по кредиту составила от 14 до 15 тысяч рублей. В ответ запишите количество миллионов.
На сторонах AB и CD четырёхугольника ABCD, около которого можно описать окружность, отмечены точки K и N соответственно. Около четырёхугольников AKND и BCNK также можно описать окружность. Косинус одного из углов четырёхугольника ABCD равен 0,2.
а) Докажите, что прямые KN и AD параллельны.
б) Найдите радиус окружности, описанной около четырёхугольника BCNK, если радиус окружности, описанной около четырёхугольника ABCD, равен 7, AK:KB=9:10, а BC< AD и BC=10.
Найдите все такие значения (a), при каждом из которых уравнение (sqrt{10x^2-19x-15}cdotlog_3(7-(a-4)(x+2))=0) имеет ровно два различных корня.
Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 7 раз больше, либо в 7 раз меньше предыдущего. Сумма всех членов последовательности равна 7735.
а) Может ли последовательность состоять из трёх членов?
б) Может ли последовательность состоять из шести членов?
в) Какое наибольшее количество членов может быть в последовательности?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Задание 12. Вариант 10 ЕГЭ 2022 Ященко
Задание 12. а) Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие отрезку [0,5; 5].
Решение.
Скорее всего, в этом задании опечатка и уравнение должно быть следующим:
а) ОДЗ уравнения: x 0. Преобразуем уравнение:
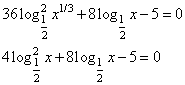
Пусть , имеем:
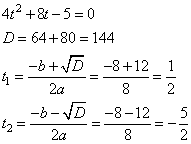
Обратная подстановка дает два уравнения:
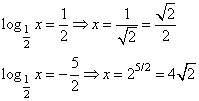
б) В диапазон [0,5; 5] попадает только один корень .
Ответ: а) ; б)
Напиши мне, решений каких вариантов не хватает на сайте?
Например: «Сборник Лысенко ЕГЭ 2023 профиль 40 вариантов», «Варианты Ларина ЕГЭ 2023 профиль», «Варианты СтатГрад ЕГЭ 2023 профиль» и т.п.
Варианты СтатГрад ЕГЭ 2023 (профильный уровень)
Варианты сборника И.В. Ященко ЕГЭ 2023 (профильный уровень), 36 вариантов.
Варианты сборника И.В. Ященко ЕГЭ 2022 (профильный уровень), 36 вариантов.
Варианты сборника И.В. Ященко ЕГЭ 2021 (профильный уровень), 36 вариантов.
Варианты сборника Ф.Ф. Лысенко ЕГЭ 2021 (профильный уровень), 40 вариантов.
Варианты сборника И.В. Ященко ЕГЭ 2020 (профильный уровень), 36 вариантов.
- ЕГЭ по математике профиль
Решение нового задания № 10 ЕГЭ 2022 по профильной математике из сборника Ященко.
На занятии рассмотрены некоторые задачи по теории вероятности из сборника с типовыми вариантами для подготовки к профильному ЕГЭ по математике 2022 под редакцией И.В. Ященко. Видео рекомендовано тем, кто владеет базовыми понятиями теории вероятности.
Видео представил YouTube канал Matesha Plus
→ Задание 10 ЕГЭ 2022 математика профильный уровень — практика
Купить ЕГЭ 2022 Математика. Профильный уровень. Типовые экзаменационные варианты. 36 вариантов
Для успешного выполнения задания 10 необходимо уметь моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий.
Связанные страницы:
Новый стрим, новый Ященко! Разбираем уравнения и неравенства из Сборника ЕГЭ-2022!
Приветствуем, друзья!
1. Заканчивается распродажа для преподавателей. Сегодня очередное подорожание онлайн-курса.
2. Многие из вас готовятся к ЕГЭ по Сборникам тренировочных вариантов ЕГЭ под редакцией И. В. Ященко. И возможно, не всё сразу получается.
Чтобы помочь вам, на стриме в четверг, 18 ноября, Анна Малкова уравнения и неравенства из Сборника «36 тренировочных вариантов ЕГЭ-2022».
Регистрируйтесь на стрим, это бесплатно!
ЖДЕМ НА СТРИМЕ!
Что будет на стриме?
Разберем задания 12 и 14 из сборника Ященко 2022 года.
Еще раз поговорим о решении и оформлении тригонометрических уравнений. Об отборе корней.
Основная тема – все-таки неравенства. Показательные, логарифмические, комбинированные.
Повторим, что такое логарифмы, и основные формулы для логарифмов.
Вспомним, что писать на бланке ЕГЭ, когда мы «отбрасываем логарифмы» (про «отбрасывание» или «откидывание» писать не надо!).
Поговорим об оформлении. Как должно выглядеть ваше решение, чтобы вы получили за него максимальный балл.
И о том, чего точно не нужно делать. Если, конечно, не хотите растерять баллы.
Стрим ведет Анна Малкова. 18 ноября, в 17.00 по московскому времени.
Регистрируемся и смотрим!
Как готовиться по Ященко?
Стоит ли готовиться к ЕГЭ-2022 по новому сборнику «36 тренировочных вариантов» под редакцией И. В. Ященко?
Наше мнение: сборник пригодится учителям и репетиторам.
Но готовиться по нему к ЕГЭ самостоятельно мы не рекомендуем.
И вот почему:
1) Задачи в вариантах неравноценны по сложности. Например, в одном варианте простейшее неравенство в № 14, в другом – сложное комбинированное.
2) Особенно это заметно для задачи 10 по теории вероятностей (новая задача). В одних вариантах – простейшие, хорошо всем знакомые задачи, например, про стекла для автомобильных фар. В других – задача про викторину, которая оказалась сложной даже для опытных преподавателей. Кстати, ее решение на этой странице под №10.
3) Решения даны только к вариантам 1, 7, 11, 17, 21, 27, 31 (7 из 36).
И вообще готовиться к ЕГЭ по сборнику заданий – плохая идея. Обычно это означает, что вы «выгрызаете» из каждого варианта несколько простых заданий, например, 6 штук из 18 задач каждого вариант. И говорите: ну вот, за пару дней прорешал треть сборника. Еще 4 дня – и подготовлюсь полностью 
Но почему-то так не происходит. И что делать со сложными задачами – непонятно. И сборник отправляется на полку.
Оптимальная отработанная подготовка
А как же надо готовиться к ЕГЭ?
Сначала – выучить необходимую теорию. Посмотреть, как решаются задачи такого типа. Затем самостоятельно работать над темой, от простых задач к сложным, и так, чтобы получать не только ответы, но и подробные решения.
Решать варианты – только на заключительном этапе тренировки!
Именно так построено обучение на Онлайн-курсе Анны Малковой.
Необходимая теория, написанная простым и понятным языком.
Видеоучебник. Как решать задачи, на что обратить внимание.
Прямые трансляции 2 раза в неделю. По 120 минут. Как с репетитором. По всем темам и задачам Профильного ЕГЭ по математике.
Онлайн-тренажер (72 темы). Все задачи – с подробными решениями и ответами.
Ответы на все ваши вопросы, помощь в решении задач.
И Пробные ЕГЭ раз в месяц.
Кстати, пора присылать решения на наш Ноябрьский Пробный ЕГЭ. Кто он нем еще не знает – читаем и регистрируемся, здесь! Это бесплатно!
Смотрим стрим Анны Малковой завтра. И идем к нам на Онлайн-курс! Это лучше, чем самостоятельно пытаться подготовиться по сборнику Ященко.
Наши Онлайн-курсы:
Для тех, кому нужна выстроенная, проверенная программа подготовки от опытных преподавателей. С нуля до самых сложных тем. Есть программы для абитуриентов и преподавателей. Посмотрите видео, как устроен курс. Оформите бесплатный демодоступ.
Математика
Физика
Информатика
Русский
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Разбираем сборник Ященко-2022!» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из Рубрики: Новости.
Публикация обновлена:
10.03.2023
Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.