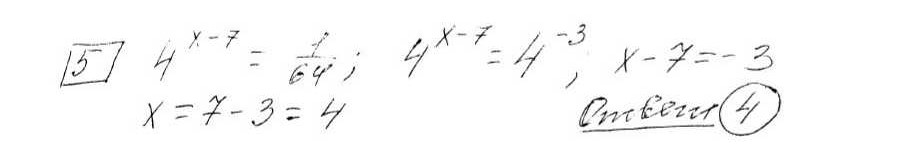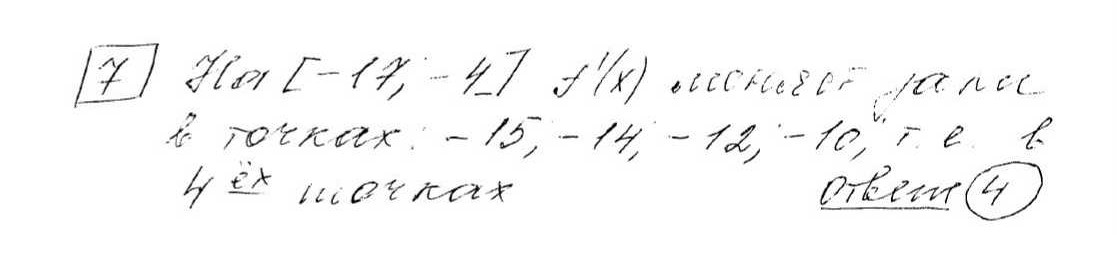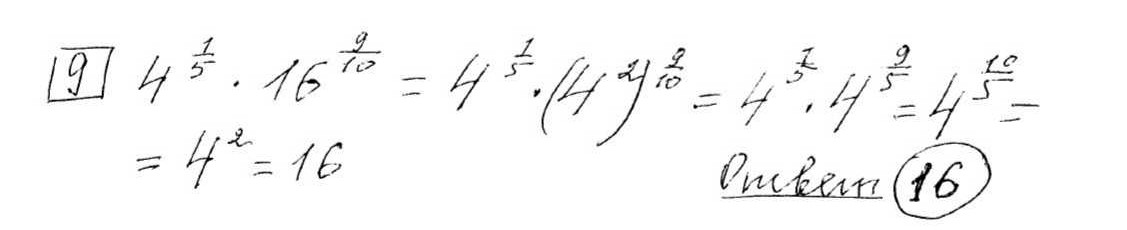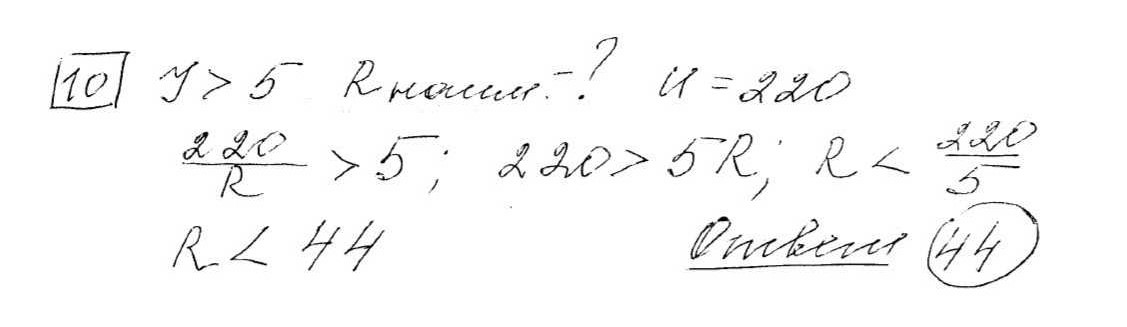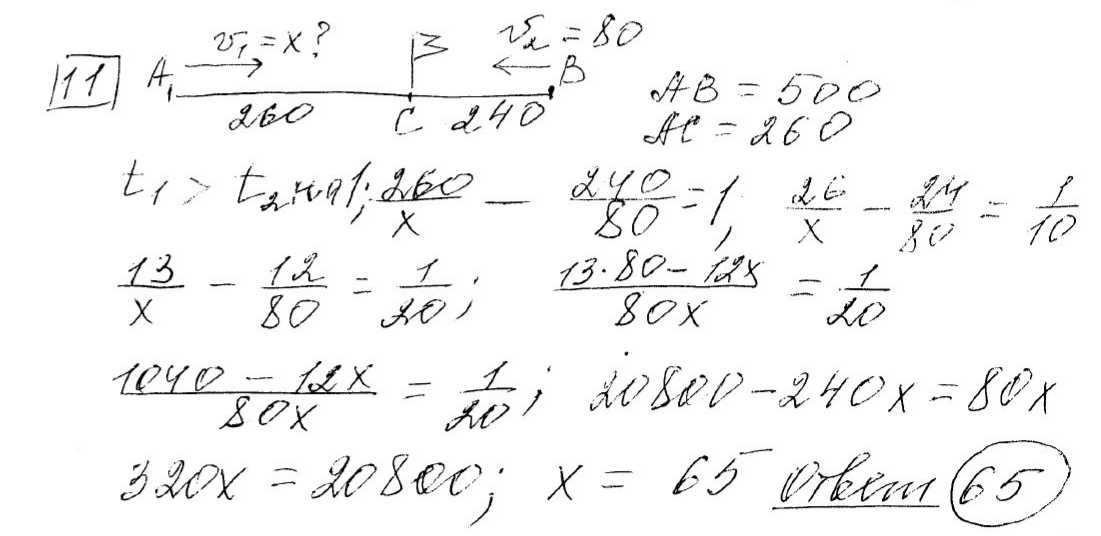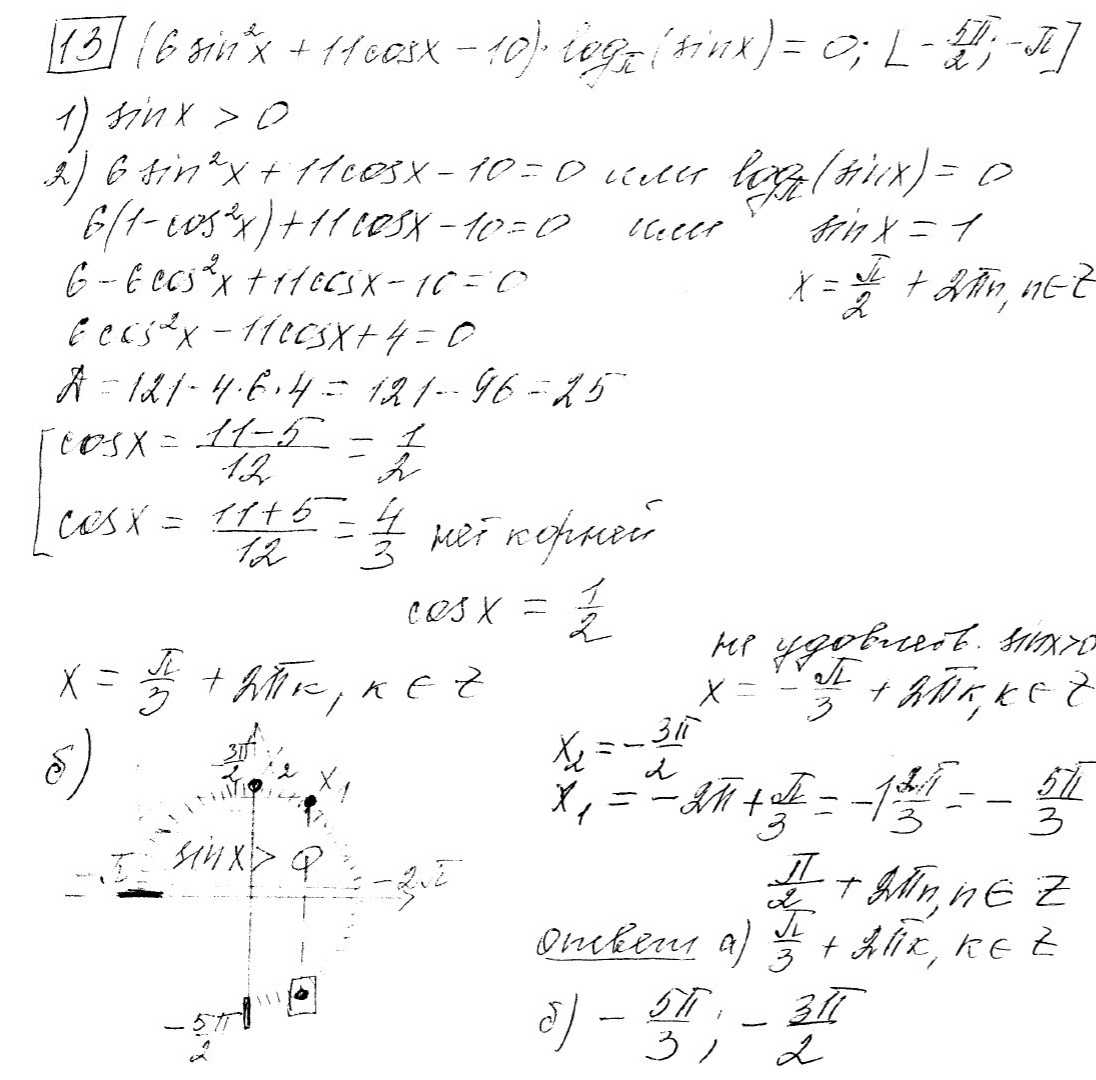Егэ математика профиль 2021 ященко 36 вариантов решение 4 вариант - Помощь в подготовке к экзаменам и поступлению

Решение и ответы заданий № 1–12 варианта №4 из сборника ЕГЭ 2021 по математике (профильный уровень) И.В. Ященко. ГДЗ профиль для 11 класса.

Задание 1.
В летнем лагере 220 детей и 24 воспитателя. Автобус рассчитан не более чем на 38 пассажиров. Какое наименьшее количество автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?

Задание 2.
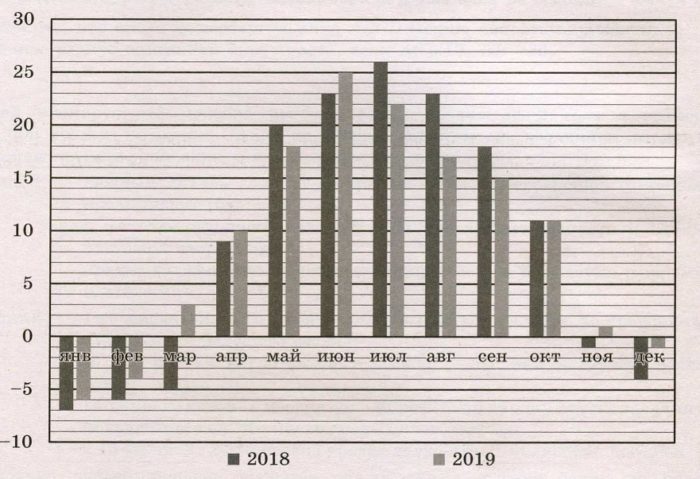
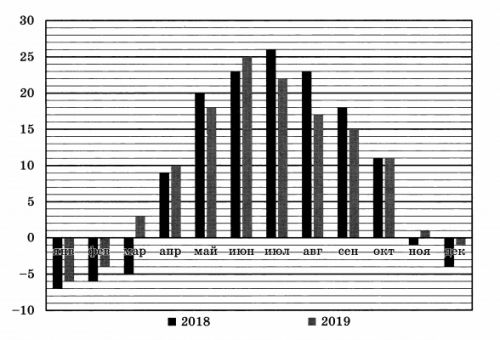
На диаграмме показано изменение средней температуры за каждый месяц в 2018 и 2019 годах в Волгограде. По горизонтали указаны месяцы, по вертикали – значение температуры в градусах Цельсия. Определите разницу между наибольшей и наименьшей среднемесячными температурами в Волгограде в 2019 году. Ответ дайте в градусах Цельсия.

Задание 3.
На клетчатой бумаге с размером клетки 1 х 1 изображён квадрат. Найдите радиус вписанной в него окружности.

Задание 4.
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей – 1 очко, если проигрывает – 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований, если вероятности выигрыша и проигрыша в каждой игре одинаковы и равны 0,4.

Задание 5.
Найдите корень уравнения log_0,5(x+5) = log₂0,2

Задание 6.
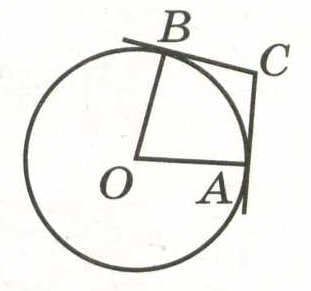
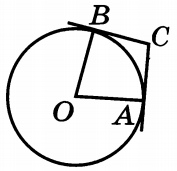
Через концы А и В дуги окружности с центром О проведены касательные СА и СВ. Угол САВ равен 39°. Найдите угол АОВ. Ответ дайте в градусах.

Задание 7.
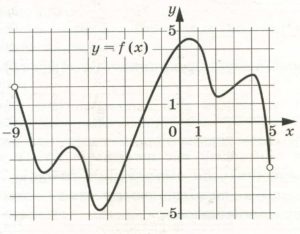
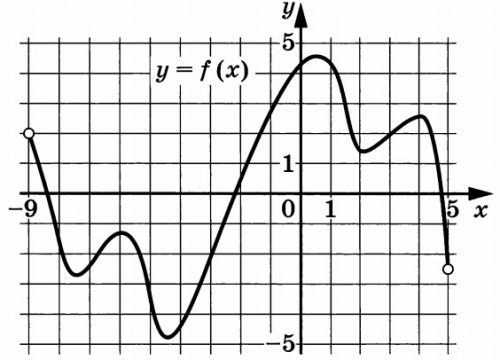
На рисунке изображён график функции у = f(x), определённой на интервале (–9; 5). Найдите количество точек, в которых производная функции f(x) равна 0.

Задание 8.
Объём параллелепипеда АВСDА₁В₁С₁D₁ равен 60. Найдите объём треугольной пирамиды АСВ₁D₁.

Задание 9.
Найдите значение выражения

Задание 10.
Мяч бросили под острым углом α к плоской горизонтальной поверхности земли. Время полёта мяча (в секундах) определяется по формуле . При каком значении угла α (в градусах) время полёта составит 1,4 секунды, если мяч бросают с начальной скоростью v₀ = 14 м/с². Считайте, что ускорение свободного падения g = 10 м/с².

Задание 11.
Смешали 3 кг 24-процентного раствора, 4 кг 32-процентного раствора и некоторое количество 48-процентного раствора одного и того же вещества. Сколько килограммов 48-процентного раствора использовали, если в результате получили 40-процентный раствор вещества?

Задание 12.
Найдите точку минимума функции y = (x + 4)²(x + 1) + 9

Источник варианта: Сборник ЕГЭ 2021 по математике профильный уровень. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.2 / 5. Количество оценок: 5

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

В летнем лагере 220 детей и 24 воспитателя. Автобус рассчитан не более чем на 38 пассажиров. Какое наименьшее количество автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?

На диаграмме показано изменение средней температуры за каждый месяц в 2018 и 2019 годах в Волгограде. По горизонтали указаны месяцы, по вертикали – значение температуры в градусах Цельсия. Определите разницу между наибольшей и наименьшей среднемесячными температурами в Волгограде в 2019 году. Ответ дайте в градусах Цельсия.

На клетчатой бумаге с размером клетки 1×1 изображен квадрат. Найдите радиус вписанной в него окружности.

Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей – 1 очко, если проигрывает – 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований, если вероятности выигрыша и проигрыша в каждой игре одинаковы и равны 0,4.

Найдите корень уравнения (log_{0{,}5}{(x+5)} = log_{2}{0{,}2}).

Через концы A и B дуги окружности с центром O проведены касательные CA и CB. Угол CAB равен 39°. Найдите угол AOB. Ответ дайте в градусах.

На рисунке изображен график функции (y = f(x)), определенной на интервале ((-9; 5)). Найдите количество точек, в которых производная функции (f(x)) равна 0.

Объём параллелепипеда ABCDA₁B₁C₁D₁ равен 60. Найдите объём треугольной пирамиды ACB₁D₁.

Найдите значение выражения (dfrac{{14}^{6{,}4} cdot 7^{-5{,}4}}{4^{2{,}2}}).

Мяч бросили под острым углом (alpha) к плоскости горизонтальной поверхности земли. Время полёта мяча (в секундах) определяется по формуле (t = dfrac{2v_0 sin{alpha}}{g}). При каком значении угла (alpha) (в градусах) время полета составит (1{,}4) секунды, если мяч бросают с начальной скоростью (v_0 = 14) м/с². Считайте, что ускорение свободного падения (g = 10) м/с².

Смешали 3 кг 24-процентного раствора, 4 кг 32-процентного раствора и некоторое количество 48-процентного раствора одного и того же вещества. Сколько килограммов 48-процентного раствора использовали, если в результате получили 40-процентный раствор вещества?

Найдите точку минимума функции (y = (x+4)^2(x+1) + 9).

a) Решите уравнение ((x^2 + 4x — 2)(4^{3x+1} + 8^{2x-1} — 11) = 0)

б) Найдите все корни уравнения, принадлежащие отрезку ([-0{,}5; 0{,}5])

В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 8, а боковое ребро SA равно 7. На рёбрах AB и SB отмечены точки M и K соответственно, причем AM = 2, SK = 1. Плоскость (alpha) перпендикулярна плоскости ABC и содержит точки M и K.

а) Докажите, что плоскость (alpha) содержит точку C.

б) Найдите площадь сечения пирамиды SABCD плоскостью (alpha).

Решите неравенство (lg^4(x^2 — 26)^4 – 4lg^2(x^2 – 26)^2 leqslant 240 ).

В четырёхугольнике ABCD противоположные стороны не параллельны. Диагонали четырёхугольника ABCD пересекаются в точке O под прямым углом и образуют четыре подобных треугольника, у каждого из которых одна из вершин – точка O.
а) Докажите, что в четырехугольник ABCD можно вписать окружность.
б) Найдите радиус вписанной окружности, если AC = 12, BD = 13.

Виктор планирует 15 декабря взять в банке кредит на 2 года в размере 1962000 рублей. Сотрудник банка предложил Виктору два различных варианта погашения кредита, описание которых приведено в таблице.

Вариант 1

– каждый январь долг возрастает на 18% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
– кредит должен быть полностью погашен за два года двумя равными платежами

Вариант 2

– 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца;
– к 15-му числу 24-го месяца кредит должен быть полностью погашен

На сколько рублей меньше окажется общая сумма выплат банку по более выгодному для Виктора варианту погашения кредита?

Найдите все значения (a), при каждом из которых система уравнений (begin{cases} y + 2 — dfrac{4}{x} = left|y + dfrac{2}{x} — 3 right| \ 2y(y+2) + 3x(ax — 2) = xy(2a+3) end{cases}) имеет более 3 решений.

Оля участвовала в викторине по истории. За каждый правильный ответ участнику начисляется 8 баллов, за каждый неверный – списывается 8 баллов, за отсутствие ответа списывается 3 балла. По результатам викторины Оля набрала 35 баллов.

а) На сколько вопросов Оля ответила правильно, если в викторине было 24 вопроса?

б) На сколько вопросов Оля не дала ответа, если в викторине было 25 вопросов?

в) На сколько вопросов Оля ответила неверно, если в викторине было 37 вопросов?

Введите ответ в форме строки «21;43;7», где ответы на пункты разделены «;».

Источник

Варианты Ященко (ЕГЭ профиль): разбор в видеоформате

На данной странице представлены ссылки на видеоразборы всех 36 вариантов из сборника Ященко 2019 года.

Источник


3631	В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 75°. Точка P лежит вне прямоугольника, а угол APB равен 150°. а) Докажите, что углы BAP и POB равны. б) Прямая PO пересекает сторону CD в точке F. Найдите CF, если AP=6sqrt3 и BP=4 Решение	В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 75° ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 16 # Задача-аналог 2559

3577	В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=5 и BC=sqrt23. Длины боковых рёбер пирамиды SA = 2sqrt15, SB=sqrt85, SD=sqrt83. а) Докажите, что SA — высота пирамиды SABCD. б) Найдите угол между прямыми SC и BD Решение	В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=5 и BC=sqrt23 ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 13 Вариант МА2210209 #Задача-аналог 2525

3244	В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания AB равна 3, а боковое ребро AA1 равно sqrt3. На ребрах C1D1 и DD1 отмечены соответственно точки K и M так, что D1K=KC1, а DM:MD1=1:3. а) Докажите, что прямые MK и BK перпендикулярны. б) Найдите угол между плоскостями BMK и ABB1 Решение	В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания AB равна 3, а боковое ребро AA1 равно sqrt 3 ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 18 Задание 13 # Задача-аналог 2574

2881	Точка O — центр вписанной в треугольник ABC окружности. Прямая BO вторично пересекает описанную около этого треугольника окружность в точке P. а) Докажите, что /_POA=/_PAO. б) Найдите площадь треугольника APO, если радиус описанной около треугольника ABC окружности равен 6, /_BAC=75^@, /_ABC=60^@ Решение	Прямая BO вторично пересекает описанную около этого треугольника окружность в точке P ! 36 вариантов ФИПИ Ященко 2022 Вариант 21 Задание 16 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 11 Задание 16 # Задача-аналог 2623

2877	В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 7. На рёбрах AB и SC отмечены точки K и M соответственно, причем AK:KB=SM:MC=1:5. Плоскость alpha содержит прямую KM и параллельна прямой BC. a) Докажите, что плоскость alpha параллельна прямой SA. б) Найдите угол между плоскостями alpha и SBC Решение	В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 7 ! 36 вариантов ФИПИ Ященко 2022 Вариант 21 Задание 13 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 11 Задание 14 # Задача-аналог 1669

2874	Для каждого натурального числа n обозначим через n! произведение первых n натуральных чисел (1! = 1). а) Существует ли такое натуральное число n, что десятичная запись числа n! оканчивается ровно 9 нулями? б) Существует ли такое натуральное число n, что десятичная запись числа n! оканчивается ровно 23 нулями? в) Сколько существует натуральных чисел n, меньших 100, для каждого из которых десятичная запись числа n∙ (100 — n)! оканчивается ровно 23 нулями Решение	Для каждого натурального числа n обозначим через n! произведение первых n натуральных чисел (1! = 1) ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 17 Задание 18 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 7 Задание 19

2873	Найдите, при каких неотрицательных значениях a функция f(x)=3ax^4-8x^3 +3x^2-7 на отрезке [-1; 1] имеет ровно одну точку минимума Решение График	Найдите, при каких неотрицательных значениях a функция f(x) на отрезке [-1; 1] имеет ровно одну точку минимума ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 17 Задание 17 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 7 Задание 18

2872	Александр хочет купить пакет акций быстрорастущей компании. В начале года у Александра не было денег на покупку акций, а пакет стоил 100 000 рублей. В середине каждого месяца Александр откладывает на покупку пакета акций одну и ту же сумму, а в конце месяца пакет дорожает, но не более чем на 30 %. Какую наименьшую сумму нужно откладывать Александру каждый месяц, чтобы через некоторое время купить желаемый пакет акций? Решение	Александр хочет купить пакет акций быстрорастущей компании ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 15 Задание 15 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 7 Задание 17

2853	а) Решите уравнение 2sin^2(x)+cos(x)-1=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [-5pi; -4pi]. Решение График	а) Решите уравнение 2sin2 x + cosx -1 = 0 ! 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 36 Задание 13

2852	За круглый стол на 21 стул в случайном порядке рассаживаются 19 мальчиков и 2 девочки. Найдите вероятность того, что девочки не окажутся на соседних местах Решение	За круглый стол на 21 стул в случайном порядке рассаживаются 19 мальчиков и 2 девочки ! 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 35 Задание 4