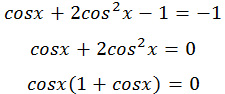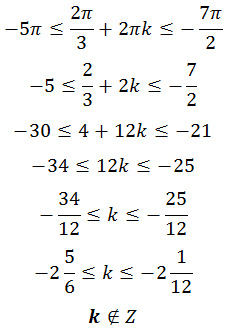Методы решения и отбора корней тригонометрических уравнений
Задание 13 профильного уровня ЕГЭ.
Программа «Профессионалитет»
Федеральный проект Министерства просвещения Российской Федерации
Задача на движение
Два человека отправляются из одного дома на прогулку до опушки леса, находящейся в 4,4 км от дома. Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от дома произойдёт их встреча? Ответ дайте в километрах.
9 задание. Анализ графика
Теория и практика по новому заданию в профильном ЕГЭ по математике.
Задание 13 ЕГЭ-2021. Решение уравнений
1. а) Решите уравнение
б) Найдите все его корни на отрезке
Решим второе уравнение;
б) Отберем корни на отрезке с помощью единичной окружности.
Отметим на единичной окружности отрезок и найдем серии решений;
Видим, что указанному отрезку принадлежат точки
2. а) Решите уравнение
б) Найдите все корни на отрезке
По формуле синуса двойного угла,
Вынесем за скобки
а так как получим:
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю.
б) Найдем корни на промежутке
1) Рассмотрим первую серию решений:
значит, из первой серии решений в указанный промежуток попадают 2 корня и
2) Рассмотрим вторую серию решений:
разделим все части неравенства на 2
Значит, из второй серии решений получаем ещё один корень
3) Рассмотрим третью серию решений:
из третьей серии получаем четвертый корень
3. а) Решить уравнение
б) Найти корни на
Применим формулы приведения:
Применим формулу синуса двойного угла:
уравнение примет вид:
б) Найдем корни на отрезке с помощью двойных неравенств.
1) Серия решений
k = 1, значит, на данном промежутке из этой серии находится только 1 корень
2) Серия решений
значит, из этой серии на данном промежутке корней нет.
3) Серия решений
значит, из этой серии на данном промежутке лежат 2 корня
Таким образом, на заданном промежутке мы нашли 3 корня:
4. (Резервный день)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
По формуле приведения,
б) Найдем корни на отрезке с помощью единичной окружности. Видим, что указанному отрезку принадлежат точки
Это полезно
Узнаете, чем отличаются официально-деловой, публицистический, научный, художественный и разговорный стили.
Наш онлайн-курс по Физике
Все темы ЕГЭ с нуля
Можно не только читать, но и смотреть новые объяснения и разборы на нашем YouTube канале!
Пожалуйста, подпишитесь на канал и нажмите колокольчик, чтобы не пропустить новые видео
Задавайте свои вопросы в комментариях и оставляйте задачи, которые вы хотите, чтобы мы разобрали.
Мы обязательно ответим!
Мы заметили, что Вы регулярно пользуетесь нашими материалами для подготовки по физике.
Результат будет выше, если готовиться по отработанной методике.
У нас есть онлайн-курсы как для абитуриентов, так и для преподавателей.
Задания по теме «Тригонометрические уравнения»
Открытый банк заданий по теме тригонометрические уравнения. Задания C1 из ЕГЭ по математике (профильный уровень)
Задание №1179
Условие
а) Решите уравнение 2(sin x-cos x)=tgx-1.
б) Укажите корни этого уравнения, принадлежащие промежутку left[ frac<3pi >2;,3pi right].
Решение
а) Раскрыв скобки и перенеся все слагаемые в левую часть, получим уравнение 1+2 sin x-2 cos x-tg x=0. Учитывая, что cos x neq 0, слагаемое 2 sin x можно заменить на 2 tg x cos x, получим уравнение 1+2 tg x cos x-2 cos x-tg x=0, которое способом группировки можно привести к виду (1-tg x)(1-2 cos x)=0.
1) 1-tg x=0, tg x=1, x=fracpi 4+pi n, n in mathbb Z;
2) 1-2 cos x=0, cos x=frac12, x=pm fracpi 3+2pi n, n in mathbb Z.
б) С помощью числовой окружности отберём корни, принадлежащие промежутку left[ frac<3pi >2;, 3pi right].
x_1=fracpi 4+2pi =frac<9pi >4,
x_2=fracpi 3+2pi =frac<7pi >3,
x_3=-fracpi 3+2pi =frac<5pi >3.
Ответ
а) fracpi 4+pi n, pmfracpi 3+2pi n, n in mathbb Z;
б) frac<5pi >3, frac<7pi >3, frac<9pi >4.
Задание №1178
Условие
а) Решите уравнение (2sin ^24x-3cos 4x)cdot sqrt =0.
б) Укажите корни этого уравнения, принадлежащие промежутку left( 0;,frac<3pi >2right] ;
Решение
а) ОДЗ: begin tgxgeqslant 0\xneq fracpi 2+pi k,k in mathbb Z. end
Исходное уравнение на ОДЗ равносильно совокупности уравнений
left[!!begin 2 sin ^2 4x-3 cos 4x=0,\tg x=0. endright.
Решим первое уравнение. Для этого сделаем замену cos 4x=t, t in [-1; 1]. Тогда sin^24x=1-t^2. Получим:
t_1=frac12, t_2=-2, t_2notin [-1; 1].
4x=pm fracpi 3+2pi n,
x=pm fracpi <12>+frac<pi n>2, n in mathbb Z.
Решим второе уравнение.
tg x=0,, x=pi k, k in mathbb Z.
При помощи единичной окружности найдём решения, которые удовлетворяют ОДЗ.
Знаком «+» отмечены 1 -я и 3 -я четверти, в которых tg x>0.
Получим: x=pi k, k in mathbb Z; x=fracpi <12>+pi n, n in mathbb Z; x=frac<5pi ><12>+pi m, m in mathbb Z.
б) Найдём корни, принадлежащие промежутку left( 0;,frac<3pi >2right].
Ответ
а) pi k, k in mathbb Z; fracpi <12>+pi n, n in mathbb Z; frac<5pi ><12>+pi m, m in mathbb Z.
Задание №1177
Условие
а) Решите уравнение: cos ^2x+cos ^2fracpi 6=cos ^22x+sin ^2fracpi 3;
б) Укажите все корни, принадлежащие промежутку left( frac<7pi >2;,frac<9pi >2right].
Решение
а) Так как sin fracpi 3=cos fracpi 6, то sin ^2fracpi 3=cos ^2fracpi 6, значит, заданное уравнение равносильно уравнению cos^2x=cos ^22x, которое, в свою очередь, равносильно уравнению cos^2x-cos ^2 2x=0.
Но cos ^2x-cos ^22x= (cos x-cos 2x)cdot (cos x+cos 2x) и
cos 2x=2 cos ^2 x-1, поэтому уравнение примет вид
(cos x-(2 cos ^2 x-1)),cdot (cos x+(2 cos ^2 x-1))=0,
(2 cos ^2 x-cos x-1),cdot (2 cos ^2 x+cos x-1)=0.
Тогда либо 2 cos ^2 x-cos x-1=0, либо 2 cos ^2 x+cos x-1=0.
Решая первое уравнение как квадратное уравнение относительно cos x, получаем:
(cos x)_<1,2>=frac<1pmsqrt 9>4=frac<1pm3>4. Поэтому либо cos x=1, либо cos x=-frac12. Если cos x=1, то x=2kpi , k in mathbb Z. Если cos x=-frac12, то x=pm frac<2pi >3+2spi , s in mathbb Z.
Аналогично, решая второе уравнение, получаем либо cos x=-1, либо cos x=frac12. Если cos x=-1, то корни x=pi +2mpi , m in mathbb Z. Если cos x=frac12, то x=pm fracpi 3+2npi , n in mathbb Z.
Объединим полученные решения:
x=mpi , m in mathbb Z; x=pm fracpi 3 +spi , s in mathbb Z.
б) Выберем корни, которые попали в заданный промежуток, с помощью числовой окружности.
Получим: x_1 =frac<11pi >3, x_2=4pi , x_3 =frac<13pi >3.
Ответ
а) mpi, m in mathbb Z; pm fracpi 3 +spi , s in mathbb Z;
б) frac<11pi >3, 4pi , frac<13pi >3.
Задание №1176
Условие
а) Решите уравнение 10cos ^2frac x2=frac<11+5ctgleft( dfrac<3pi >2-xright) ><1+tgx>.
б) Укажите корни этого уравнения, принадлежащие интервалу left( -2pi ; -frac<3pi >2right).
Решение
а) 1. Согласно формуле приведения, ctgleft( frac<3pi >2-xright) =tgx. Областью определения уравнения будут такие значения x , что cos x neq 0 и tg x neq -1. Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 cos ^2 frac x2=1+cos x. Получим уравнение: 5(1+cos x) =frac<11+5tgx><1+tgx>.
Заметим, что frac<11+5tgx><1+tgx>= frac<5(1+tgx)+6><1+tgx>= 5+frac<6><1+tgx>, поэтому уравнение принимает вид: 5+5 cos x=5 +frac<6><1+tgx>. Отсюда cos x =frac<dfrac65><1+tgx>, cos x+sin x =frac65.
2. Преобразуем sin x+cos x по формуле приведения и формуле суммы косинусов: sin x=cos left(fracpi 2-xright), cos x+sin x= cos x+cos left(fracpi 2-xright)= 2cos fracpi 4cos left(x-fracpi 4right)= sqrt 2cos left( x-fracpi 4right) = frac65.
Отсюда cos left(x-fracpi 4right) =frac<3sqrt 2>5. Значит, x-fracpi 4= arccos frac<3sqrt 2>5+2pi k, k in mathbb Z,
или x-fracpi 4= -arccos frac<3sqrt 2>5+2pi t, t in mathbb Z.
Поэтому x=fracpi 4+arccos frac<3sqrt 2>5+2pi k,k in mathbb Z,
или x =fracpi 4-arccos frac<3sqrt 2>5+2pi t,t in mathbb Z.
Найденные значения x принадлежат области определения.
б) Выясним сначала куда попадают корни уравнения при k=0 и t=0. Это будут соответственно числа a=fracpi 4+arccos frac<3sqrt 2>5 и b=fracpi 4-arccos frac<3sqrt 2>5.
1. Докажем вспомогательное неравенство:
Заметим также, что left( frac<3sqrt 2>5right) ^2=frac<18> <25>значит frac<3sqrt 2>5
2. Из неравенств (1) по свойству арккосинуса получаем:
Отсюда fracpi 4+0
Аналогично, -fracpi 4
0=fracpi 4-fracpi 4 fracpi 4
При k=-1 и t=-1 получаем корни уравнения a-2pi и b-2pi.
Bigg( a-2pi =-frac74pi +arccos frac<3sqrt 2>5,, b-2pi =-frac74pi -arccos frac<3sqrt 2>5Bigg). При этом -2pi
-2pi Значит, эти корни принадлежат заданному промежутку left( -2pi , -frac<3pi >2right).
При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.
Действительно, если kgeqslant 1 и tgeqslant 1, то корни больше 2pi. Если kleqslant -2 и tleqslant -2, то корни меньше -frac<7pi >2.
Ответ
а) fracpi4pm arccosfrac<3sqrt2>5+2pi k, kinmathbb Z;
б) -frac<7pi>4pm arccosfrac<3sqrt2>5.
Задание №1175
Условие
а) Решите уравнение sin left( fracpi 2+xright) =sin (-2x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [0; pi ];
Решение
а) Преобразуем уравнение:
cos x+2 sin x cos x=0,
x =fracpi 2+pi n, n in mathbb Z;
x=(-1)^cdot fracpi 6+pi k, k in mathbb Z.
б) Корни, принадлежащие отрезку [0; pi ], найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число fracpi 2.
Ответ
а) fracpi 2+pi n, n in mathbb Z; (-1)^cdot fracpi 6+pi k, k in mathbb Z;
б) fracpi 2.
Задание №1174
Условие
б) Найдите все корни этого уравнения, принадлежащие отрезку left[ -frac<3pi ><2>; -frac<pi >2 right].
Решение
а) Найдём ОДЗ уравнения: cos 2x neq -1, cos (pi +x) neq -1; Отсюда ОДЗ: x neq frac pi 2+pi k,
k in mathbb Z, x neq 2pi n, n in mathbb Z. Заметим, что при sin x=1, x=frac pi 2+2pi k, k in mathbb Z.
Полученное множество значений x не входит в ОДЗ.
Значит, sin x neq 1.
Разделим обе части уравнения на множитель (sin x-1), отличный от нуля. Получим уравнение frac 1<1+cos 2x>=frac 1<1+cos (pi +x)>, или уравнение 1+cos 2x=1+cos (pi +x). Применяя в левой части формулу понижения степени, а в правой — формулу приведения, получим уравнение 2 cos ^2 x=1-cos x. Это уравнение с помощью замены cos x=t, где -1 leqslant t leqslant 1 сводим к квадратному: 2t^2+t-1=0, корни которого t_1=-1 и t_2=frac12. Возвращаясь к переменной x , получим cos x = frac12 или cos x=-1, откуда x=frac pi 3+2pi m, m in mathbb Z, x=-frac pi 3+2pi n, n in mathbb Z, x=pi +2pi k, k in mathbb Z.
б) Решим неравенства
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 ,
2) -frac<3pi >2 leqslant -frac pi 3+2pi n leqslant -frac pi
3) -frac<3pi >2 leqslant pi+2pi k leqslant -frac pi 2 , m, n, k in mathbb Z.
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 , -frac32 leqslant frac13+2m leqslant -frac12 -frac<11>6 leqslant 2m leqslant -frac56 , -frac<11> <12>leqslant m leqslant -frac5<12>.
Нет целых чисел, принадлежащих промежутку left [-frac<11><12>;-frac5<12>right] .
2) -frac <3pi>2 leqslant -frac<pi >3+2pi n leqslant -frac<pi ><2>, -frac32 leqslant -frac13 +2n leqslant -frac12 , -frac76 leqslant 2n leqslant -frac1<6>, -frac7 <12>leqslant n leqslant -frac1<12>.
Нет целых чисел, принадлежащих промежутку left[ -frac7 <12>; -frac1 <12>right].
3) -frac<3pi >2 leqslant pi +2pi kleqslant -frac<pi >2, -frac32 leqslant 1+2kleqslant -frac12, -frac52 leqslant 2k leqslant -frac32, -frac54 leqslant k leqslant -frac34.
Этому неравенству удовлетворяет k=-1, тогда x=-pi.
Ответ
а) frac pi 3+2pi m; -frac pi 3+2pi n; pi +2pi k, m, n, k in mathbb Z;
источники:
http://ege-study.ru/ru/ege/podgotovka/matematika/ege-2021-reshenie-zadachi-13/
http://academyege.ru/theme/trigonometricheskie-uravneniya-3.html
Уравнения, содержащие задание на отбор корней
| 1 | а) Решите уравнение 7cos^{2}{x}-cos{x}-8=0 б) Найдите все корни этого уравнения, принадлежащие промежутку [-frac{7pi}{2}; -frac{3pi}{2}] |
Смотреть видеоразбор |
| 2 | а) Решите уравнение frac{6}{cos^{2}{x}}-frac{7}{cos{x}}+1=0 б) Найдите все корни этого уравнения, принадлежащие промежутку [-3pi; pi] |
Смотреть видеоразбор |
| 3 | а) Решите уравнение 3cos^{2}{x}-4sin{x}+4=0 б) Найдите все корни этого уравнения, принадлежащие промежутку [-frac{5pi}{2}; pi] |
Смотреть видеоразбор |
| 4 | а) Решите уравнение 2cos{2x}-12cos{x}+7=0 б) Найдите все корни этого уравнения, принадлежащие промежутку [-pi; frac{5pi}{2}] |
Смотреть видеоразбор |
| 5 | а) Решите уравнение frac{5}{tg^{2}x}-frac{19}{sin{x}}+17=0 б) Найдите все корни этого уравнения, принадлежащие промежутку [-frac{7pi}{2}; -2pi] |
Смотреть видеоразбор |
| 6 | а) Решите уравнение cos{2x}=1-cos(frac{pi}{2}-x) б) Найдите все корни этого уравнения, принадлежащие промежутку [-frac{5pi}{2};-pi) |
Смотреть видеоразбор |
| 7 | а) Решите уравнение cos{2x}=sin(frac{3pi}{2}-x) б) Найдите все корни этого уравнения, принадлежащие промежутку [frac{3pi}{2}; frac{5pi}{2}] |
Смотреть видеоразбор |
| 8 | а) Решите уравнение 2sin^{2}(frac{3pi}{2}+x)=sqrt{3}cos{x} б) Найдите все корни этого уравнения, принадлежащие промежутку [-frac{7pi}{2}; -2pi] |
Смотреть видеоразбор |
Уравнения, в которых отбор явно не указан, но возникает при исследовании ОДЗ
Нестандартные уравнения
Задание 13 ЕГЭ математика профильный уровень посвящен уравнениям. Раздел содержит 79 задач. В первых 15 задачах нужно решить тригонометрическое уравнение и отобрать его корни, лежащие в заданном интервале. Задание 17 содержит линейное уравнение. В задании 18 нужно найти значение тригонометрического выражения, а в задании 19 найти значение тригонометрической функции. Остальные задания содержат стандартные задачи на решение тригонометрических и алгебраических уравнений различного уровня сложности. Есть задачи на нахождение области определения и области значений заданной функции.
Этот документ можно скачать по ссылке
Полезная информация
Смотреть все
1. а) Решите уравнение
б) Найдите все его корни на отрезке
Решение:
Решим второе уравнение;
сделаем замену
получим:
б) Отберем корни на отрезке с помощью единичной окружности.
Отметим на единичной окружности отрезок и найдем серии решений;
Видим, что указанному отрезку принадлежат точки
Ответ:
а)
б)
2. а) Решите уравнение
б) Найдите все корни на отрезке
Решение:
а)
По формуле синуса двойного угла,
Вынесем за скобки
а так как
получим:
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю.
б) Найдем корни на промежутке
1) Рассмотрим первую серию решений:
Решим неравенство
значит, из первой серии решений в указанный промежуток попадают 2 корня и
2) Рассмотрим вторую серию решений:
Решим неравенство
разделим все части неравенства на 2
Значит, из второй серии решений получаем ещё один корень
3) Рассмотрим третью серию решений:
из третьей серии получаем четвертый корень
Ответ: а)
б)
3. а) Решить уравнение
б) Найти корни на
Решение:
Применим формулы приведения:
Применим формулу синуса двойного угла:
уравнение примет вид:
б) Найдем корни на отрезке с помощью двойных неравенств.
1) Серия решений
k = 1, значит, на данном промежутке из этой серии находится только 1 корень
2) Серия решений
значит, из этой серии на данном промежутке корней нет.
3) Серия решений
значит, из этой серии на данном промежутке лежат 2 корня
Таким образом, на заданном промежутке мы нашли 3 корня:
Ответ:
а)
б)
4. (Резервный день)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение:
По формуле приведения,
б) Найдем корни на отрезке с помощью единичной окружности. Видим, что указанному отрезку принадлежат точки
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 13 ЕГЭ-2021. Решение уравнений» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
Задание. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение:
а) Решите уравнение
ОДЗ уравнения: R
Преобразуем уравнение, воспользуемся формулой сложения cos(a — b) = cosa·cosb + sina·sinb, получим
Используя формулу двойного аргумента cos2a = 2cos2a — 1, получим
Значит, cosx = 0 или 1 + cosx = 0.
Решим 1 уравнение:
cosx = 0
(1)
Решим 2 уравнение:
1 + cosx = 0
cosx = — 1
(2)
(3)
б) Укажите корни этого уравнения, принадлежащие отрезку
Выберем корни уравнения при помощи единичной окружности
Корни уравнения можно выбрать другим способом:
Для первого корня: Для второго корня:
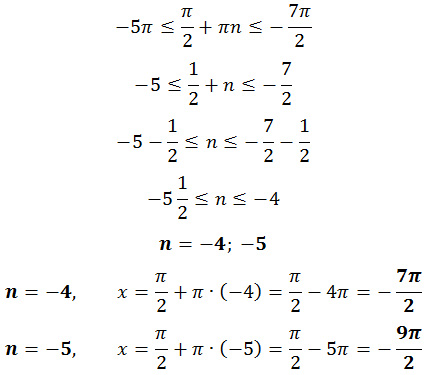
Для третьего корня:
Ответ:









.png)