Ответы на тренировочный вариант №108 профильного ЕГЭ
А. Ларин: Тренировочный вариант № 108.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Дано уравнение
а) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В равнобедренном треугольнике ABC (AB = BC) проведены биссектрисы AK, BM, CP.
а) Докажите, что треугольник KMP — равнобедренный.
б) Найдите площадь треугольника KMP, если известно, что площадь треугольника ABC равна 64, а косинус угла ВАС равен 0,3.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
{}
В правильной четырёхугольной пирамиде боковое ребро равно 3, а сторона основания равна $sqrt{10} $. Найдите высоту пирамиды.
Ответ:
5
Три свечи имеют одинаковую длину, но разную толщину. Третья свеча была зажжена на час раньше двух других, зажженных одновременно. В некоторый момент горения первая свеча и третья свечи стали одинаковой длины, а через 2 часа после этого одинаковой длины стали третья и вторая свечи. За сколько часов сгорает третья свеча, если вторая сгорает за 6 ч, а первая — за 4 ч?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения a, при каждом из которых наименьшее значение функции на отрезке [−1; 3] не меньшее, чем −5.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
А) Докажите, что среди произвольных 11 натуральных чисел всегда найдутся два, разность которых кратна 10.
Б) Докажите, что среди произвольных 11 целых чисел всегда найдутся два, разность которых кратна 10.
В) Докажите, что среди произвольных 10 натуральных чисел всегда найдутся несколько, сумма которых делится на 10.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Вопрос B1 #1613
Оптовая цена подсолнечного масла составляет 48300 рублей за тонну. Какое наибольшее число тонн подсолнечного масла можно купить на 100000 рублей, если оно продаётся коробками, в каждой из которых 20 бутылок масла по 600 г?
Вопрос B2 #1614
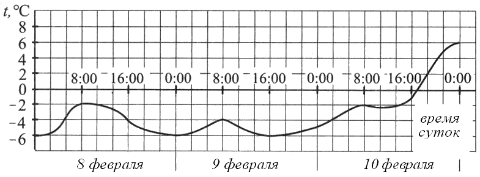
На графике показано изменение температуры воздуха в период с 8 по 10 февраля в некотором городе. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Найдите разность между наибольшим и наименьшим значениями температуры 9 февраля. Ответ дайте в градусах Цельсия
Вопрос B3 #1615
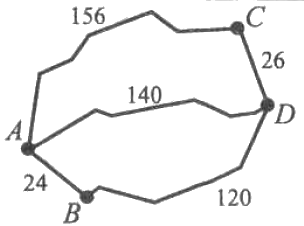
Из пункта (A) в пункт (D) ведут три дороги. Три машины одновременно выехали из (A). Через пункт (B) едет грузовая автомашина со средней скоростью 48 км/ч, через пункт (C) едет автобус со средней скоростью 52 км/ч. Третья дорога – без промежуточных пунктов, и по ней движется легковой автомобиль со средней скоростью 40 км/ч. На рисунке показана схема дорог и расстояние между пунктами по дорогам. Какая машина добралась до (D) раньше других? В ответе укажите количество часов, которое она находилась в дороге.
Вопрос B4 #1616
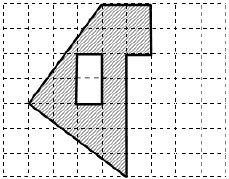
На рисунке клетка имеет размер 1 см х 1 см. Найдите периметр фигуры, изображенной на рисунке. Ответ дайте в сантиметрах
Вопрос B5 #1617
При подготовке к зачётам по алгебре и математическому анализу студент выучил по алгебре 27 вопросов из 40, а по математическому анализу — 20 вопрос из 30. Чтобы получить «зачёт» по предмету, студенту необходимо ответить на один вопрос, случайным образом выбранный из списка вопросов по данному предмету. Какова вероятность, что студент не получит «зачёт» хотя бы по одному из этих двух предметов?
Вопрос B6 #1618
Найдите корень уравнения (x^{2}+9=(x+9)^{2}).
Вопрос B7 #1619
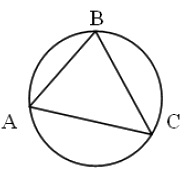
В треугольнике (ABC) угол (A) равен (45^{circ}), а сторона (BC) равна (3 sqrt{2}) . Найдите радиус окружности, описанной около треугольника (ABC).
Вопрос B8 #1620
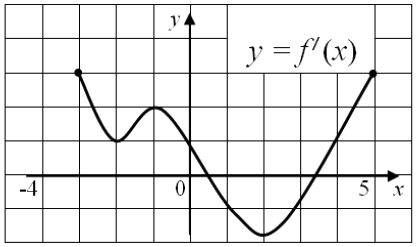
Функция (y = f (x)) определена на промежутке ([-3; 5]). На рисунке приведен график её производной. Найдите количество точек графика функции (y = f (x)), касательная в которых образует с положительным направлением оси абсцисс угол (135^{circ})
Вопрос B9 #1621
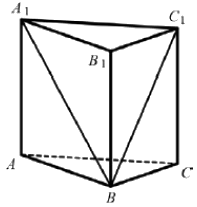
Найдите объем правильной треугольной призмы (ABCA_1 B_1 C_1), если объем многогранника, вершинами которого являются точки (A, B, C, A_1,C_1), равен (36).
Вопрос B10 #1622
Вычислите (frac{log_{3}5 cdot log_{5}8}{log_{3}4}).
Вопрос B11 #1623
Рейтинг (R) интернет-магазина вычисляется по формуле (R=r_{пок}- frac{r_{пок}-r_{экс}}{(k+1) cdot frac{0,02K}{r_{пок}+0,1}}) , где (r_{пок}) — средняя оценка магазина покупателями (от 0 до 1), (r_{экс}) – оценка магазина экспертами (от 0 до 0,7) и К – число покупателей, оценивших магазин. Найдите рейтинг интернет‐магазина, если число покупателей, оставивших отзыв о магазине, равно 24, их средняя оценка равна 0,7, а оценка экспертов равна 0,4.
Вопрос B12 #1624
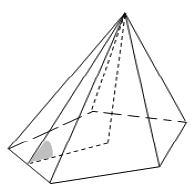
В правильной пятиугольной пирамиде двугранный угол при стороне основания равен (60^{circ}). Найдите площадь основания пирамиды, если площадь ее боковой поверхности равна (20).
Вопрос B13 #1625
Зимой цена на яблоки повысилась на 25% по сравнению с осенью. На сколько процентов заготовителю нужно уменьшить количество приобретаемых зимой яблок, чтобы затраты на их покупку увеличились только на 2,5% по сравнению с осенью?
Вопрос B14 #1626
К графику функции (f(x)=2x^{2}+1) через точку (B (3; 1)) проведена касательная, не параллельная оси абсцисс. Найдите угловой коэффициент этой касательной.
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также: