Егэ математика повышенный уровень - Помощь в подготовке к экзаменам и поступлению

Анна Малкова

В 2022 году в варианты ЕГЭ по математике добавились новые задачи по теории вероятностей. По сравнению с теми, которые раньше были в варианте, это повышенный уровень сложности.

Мы разберем задачу №4 из Демоверсии ЕГЭ-2022, задания из Методических рекомендаций ФИПИ для учителей и аналогичные им.

БЕСПЛАТНЫЙ МИНИ-КУРС ПО ТЕОРВЕРУ

1. Демоверсия ЕГЭ-2022

Симметричную игральную кость бросили 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало 3 очка»?

Решение:

Выпишем возможные исходы как тройки чисел так, чтобы в сумме получилось 6.

Всего 10 возможных исходов. Благоприятные исходы помечены красным цветом, их 6.

По определению вероятности получаем

2. Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найдите вероятность того, что во второй раз выпало 3 очка.

Решение:

Выпишем возможные варианты получения 8 очков в сумме:

Подходит только вариант 5; 3. Вероятность этого события равна 1 : 5 = 0,2 (один случай из 5 возможных).

Ответ: 0,2.

3. В ящике 4 красных и 2 синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?

Решение:

Благоприятными будут следующие исходы:

Первый раз – вытащили красный фломастер.

И второй раз – красный.

А третий раз – синий.

Вероятность вытащить красный фломастер (которых в ящике 4) равна $displaystyle frac{4}{6} = frac{2}{3}.$

После этого в ящике остается 5 фломастеров, из них 3 красных, вероятность вытащить красный равна $displaystyle frac{3}{5}.$

Наконец, когда осталось 4 фломастера и из них 2 синих, вероятность вытащить синий равна $displaystyle frac{1}{2}.$

Вероятность события {красный – красный – синий } равна произведению этих вероятностей, то есть

$displaystyle frac{2}{3} cdotfrac{3}{5} cdotfrac{1}{2} = frac{1}{5} = 0,2.$

Ответ: 0,2.

4. В коробке 10 синих, 9 красных и 6 зеленых фломастеров. Случайным образом выбирают 2 фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?

Решение:

Всего в коробке 25 фломастеров.
В условии не сказано, какой из фломастеров вытащили первым – красный или синий.

Предположим, что первым вытащили красный фломастер. Вероятность этого $displaystyle frac{9}{25},$ в коробке остается 24 фломастера, и вероятность вытащить вторым синий равна $displaystyle frac{10}{24}.$ Вероятность того, что первым вытащили красный, а вторым синий, равна $displaystyle frac{9}{25} cdot frac{10}{24}=frac{3}{5}cdot frac{1}{4} = frac{3}{20}.$

А если первым вытащили синий фломастер? Вероятность этого события равна $displaystyle frac{10}{25} = frac{2}{5}.$ Вероятность после этого вытащить красный равна $displaystylefrac{9}{24} = frac{3}{8},$ вероятность того, что синий и красный вытащили один за другим, равна $displaystylefrac{2}{5} cdot frac{3}{8} = frac{3}{20}.$

Значит, вероятность вытащить первым красный, вторым синий или первым синий, вторым красный равна $displaystylefrac{3}{20} + frac{3}{20} = 0,3.$

А если их доставали из коробки не один за другим, а одновременно? Вероятность остается такой же: 0,3. Потому что она не зависит от того, вытащили мы фломастеры один за другим, или с интервалом в 2 секунды, или с интервалом в 0,5 секунды… или одновременно!
Ответ: 0,3.

5. При подозрение на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 86 % случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 94% случаев.

Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание?

Решение:

Уточним условие: «Какова вероятность того, что пациент, ПЦР-тест которого положителен, действительно имеет это заболевание?». В такой формулировке множество возможных исходов — это число пациентов с положительным результатом ПЦР-теста, причем только часть из них действительно заболевшие.

Пациент приходит к врачу и делает ПЦР-тест. Он может быть болен этим заболеванием – с вероятностью х. Тогда с вероятностью 1 – х он этим заболеванием не болен.

Анализ пациента может быть положительным по двум причинам:
а) пациент болеет заболеванием, которое нельзя называть, его анализ верен; событие А;
б) пациент не болен этим заболеванием, его анализ ложно-положительный, событие В.
Это несовместные события, и вероятность их суммы равна сумме вероятностей этих событий.

Имеем:

Мы составили уравнение, решив которое, найдем вероятность x.

x=0,05.

Что такое вероятность х? Это вероятность того, что пациент, пришедший к доктору, действительно болен. Здесь множество возможных исходов — это количество всех пациентов, пришедших к доктору.

Нам же нужно найти вероятность z того, что пациент, ПЦР-тест которого положителен, действительно имеет это заболевание. Вероятность этого события равна (пациент болен и ПЦР-тест выявил заболевание, произведение событий). С другой стороны, эта вероятность равна (у пациента положительный результат ПЦР-теста, и при выполнении этого условия он действительно болен).

Получим: отсюда

Ответ: 0,43.

Вероятность того, что пациент с положительным результатом ПЦР-теста действительно болен, меньше половины!
Кстати, это реальная проблема для диагностики в медицине, то есть в задаче отражена вполне жизненная ситуация.

Лень разбираться самому?
Присоединяйся к мини-курсу по теории вероятностей

ПОДРОБНЕЕ

6. Телефон передает sms-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой следующей попытке, равна 0,4. Найдите вероятность того, что для передачи сообщения потребуется не больше 2 попыток.

Решение:
Здесь все просто. Либо сообщение удалось передать с первой попытки, либо со второй.
Вероятность того, что сообщение удалось передать с первой попытки, равна 0,4.

С вероятностью 0,6 с первой попытки передать не получилось. Если при этом получилось со второй, то вероятность этого события равна

Значит, вероятность того, что для передачи сообщения потребовалось не более 2 попыток, равна

Ответ: 0,64.

7. Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?

Решение:

А это более сложная задача. Можно, как и в предыдущих, пользоваться определением вероятности и понятиями суммы и произведения событий. А можно применить формулу Бернулли.

Формула Бернулли:

– Вероятность P^m_n того, что в n независимых испытаниях некоторое случайное событие A наступит ровно m раз, равна:

$P^m_n = C^m_n p^m q^{n-m},$ где

p – вероятность появления события A в каждом испытании;

q=1-p – вероятность появления события A в каждом испытании.

Коэффициент C^m_n часто называют биномиальным коэффициентом.

О том, что это такое, расскажем с следующих статьях на нашем сайте. Чтобы не пропустить – подписывайтесь на нашу рассылку.

А пока скажем просто, как их вычислять.

$displaystyle C^m_n = frac{n!}{m!(n-m)!}.$

Нет, это не заклинание. Не нужно громко кричать: Эн!!!! Поделить на эм! И на эн минус эм! То, что вы видите в формуле, – это не восклицательные знаки. Это факториалы. На самом деле все просто: n! (читается: эн факториал) – это произведение натуральных чисел от 1 до n. Например,

Пусть вероятность выпадения орла при одном броске монеты равна $displaystylefrac{1}{2},$ вероятность решки тоже $displaystyle frac{1}{2}.$ Давайте посчитаем вероятность того, что из 10 бросков монеты выпадет ровно 5 орлов.

$displaystyle P_1=C_{10}^5left ( frac{1}{2} right )^5cdot left ( frac{1}{2} right )^5=frac{10!}{5!cdot 5!cdot 2^{10}}.$

Вероятность выпадения ровно 4 орлов равна

$displaystyle P_2=C_{10}^4cdot left ( frac{1}{2} right )^4cdot left ( frac{1}{2} right )^6=frac{10!}{4!cdot 6!cdot 2^{10}}.$

Найдем, во сколько раз P_1 больше, чем P_2.

$displaystyle frac{P_1}{P_2}=frac{10!cdot 4!cdot 6!cdot 2^{10}}{5!cdot 5!cdot 2^{10}cdot 10!}=frac{4!}{5!}=frac{1cdot 2cdot 3cdot 4cdot 1cdot 2cdot 3 cdot 4cdot 5cdot 6}{1cdot 2cdot 3cdot 4cdot 5 cdot 1cdot 2cdot 3 cdot 4cdot 5}=$

$displaystyle =frac{6}{5} = 1,2.$

Ответ: 1,2.

8. Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько раз вероятность события «стрелок поразит ровно 5 мишеней» больше вероятности события «стрелок поразит ровно 4 мишени»?

Решение:

Стрелок поражает мишень с первого или со второго выстрела;
Вероятность поразить мишень равна

Вероятность поразить 5 мишеней из 5 равна

Вероятность поразить 4 мишени из 5 находим по формуле Бернулли:

$displaystyle P_2=C_{5}^{4}cdot 0,84^{4}cdot 0,16=frac{5!; 0,84^4 cdot 0,16}{4!}=5cdot 0,84^4 cdot 0,16.$

$displaystyle frac{P_1}{P_2} = frac{0,84^5}{5 cdot 0,84^4 cdot 0,16}= frac{0,84}{0,8}=1,05.$

9. Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов, и известно, что вероятность поразить мишень каждым выстрелом равна 0,5. Во сколько раз вероятность события «стрелок поразит ровно 3 мишени» больше вероятности события «стрелок поразит ровно 2 мишени»?

Решение:
Найдем вероятность поразить одну мишень – с первого или со второго выстрела.

С вероятностью $displaystyle frac{1}{2}$ стрелок поражает мишень первым выстрелом (и больше по ней не стреляет).

Найдем вероятность того, что стрелок поразит мишень вторым выстрелом. Она равна $displaystyle frac{1}{2} cdot frac{1}{2} = frac{1}{4},$ так как с вероятностью $displaystyle frac{1}{2}$ он промахнулся в первый раз и с вероятностью $displaystyle frac{1}{2}$ второй выстрел был удачным.

Значит, вероятность поразить одну мишень первым или вторым выстрелом равна $displaystyle frac{1}{2}+frac{1}{4} = frac{3}{4}.$

Теперь нам на помощь придет формула Бернулли.

Найдем вероятность того, что стрелок поразит ровно 3 мишени из 5.

$displaystyle P_1=P^3_5=C^3_5 cdot left ( frac{3}{4} right )^3 cdot left ( frac{1}{4} right )^2 = frac{5!}{3! 2!} cdot frac{3^3}{4^5}.$

Вероятность поразить ровно 2 мишени из пяти

$displaystyle P_2=P^2_5=C^2_5 cdot left ( frac{3}{4} right )^2cdot left( frac{1}{4} right )^3 = frac{5!}{3! 2!} cdot frac{3^2}{4^5}.$

Заметим, что

Получим:

$displaystyle frac{P_1}{P_2} = frac{3^3 cdot 4^5}{4^5 cdot 3^2} = 3.$

Ответ: 3.

10. Стрелок в тире стреляет по мишени. Известно, что он попадает в цель с вероятностью 0,3 при каждом отдельном выстреле. Какое наименьшее количество патронов нужно дать этому стрелку, чтобы вероятность поражения цели была не менее 0,6?

Решение:

Похожие задачи были в Банке заданий ФИПИ и раньше. Пусть у стрелка есть n патронов. Стрелок может поразить цель первым, вторым … n-ным выстрелом, и все эти исходы для нас благоприятны. Не подходит только один исход – когда стрелок n раз стрелял и каждый раз был промах.

Вероятность промаха при одном выстреле равна 1 – 0,3 = 0,7.

Вероятность n промахов (из n выстрелов) равна 0,7^n, а вероятность попасть с первого раза или сто второго … или с n-ого выстрела равна

По условию,

Если n = 2, то – не подходит.

Для n=3 условие выполнено,

Хватит 3 патронов.

Ответ: 3.

11. Игральную кость бросают до тех пор, пока сумма всех выпавших очков не превысит число 3. Какова вероятность того, что для этого потребуется ровно 3 броска? Ответ округлите до сотых.

Решение:

Кажется, что задача сложная (на самом деле нет).

Давайте подумаем: как получилось, что ровно за 3 броска игральной кости сумма выпавших очков оказалась больше трех? Из этого следует, что за 2 броска сумма выпавших очков была меньше 3 или равна 3.

Если за 2 броска сумма выпавших очков была меньше 3, значит, она была равна 2, то есть первый раз выпала единица и второй раз тоже единица. Вероятность этого события равна $displaystyle frac{1}{6} cdot frac{1}{6} = frac{1}{36}.$

Сколько же очков в этом случае должен дать третий бросок? Очевидно, что подойдет 2, 3, 4, 5, 6 – все, кроме 1. Вероятность того, что при третьем броске выпадет число очков, не равное единице, равна $displaystyle frac{5}{6}.$

Значит, вероятность того, что при первых двух бросках выпали единицы, а при третьем – не единица, равна $displaystyle frac{5}{216}.$

Нам подойдет также случай, когда сумма очков за первые 2 броска равна 3. Это значит, что выпали 2 и 1 или 1 и 2, то есть 2 благоприятных исхода из 36 возможных. Вероятность этого события равна $displaystyle frac{2}{36} = frac{1}{18}.$

При этом нам все равно, что выпадет при третьем броске: очевидно, что сумма очков при трех бросках будет больше трех.

Окончательно получаем: $displaystyle frac{5}{216} + frac{1}{18} = frac{17}{216} approx 0,08.$

Ответ: 0,08.

Вот еще одна задача из Демоверсии ЕГЭ-2022:

12. В городе 48% взрослого населения – мужчины. Пенсионеры составляют 12,6% взрослого населения, причём доля пенсионеров среди женщин равна 15%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».

Решение:
Пусть N – численность взрослого населения в городе (мужчин и женщин).
Количество взрослых мужчин в городе: 0,48N.
Количество женщин в городе: 0,52N.
Из них 0,15 * 0,52N = 0,078N женщин-пенсионеров.
Всего пенсионеров 0,126N.
Тогда количество мужчин-пенсионеров равно 0,126N – 0,078N = 0,048N.
Вероятность для случайно выбранного мужчины оказаться пенсионером равна отношению числа мужчин-пенсионеров к числу мужчин в городе, то есть 0,048 N : 0,48N = 0,1.
Ответ. 0,1.

Мы разобрали все доступные типы заданий №4 из вариантов ЕГЭ-2022. Раздел будет дополняться решениями новых задач – как только они появятся в Банке заданий ФИПИ.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 4 ЕГЭ по математике. Теория вероятностей. Повышенный уровень сложности» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.

Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.admin2023-03-05T21:56:54+03:00

Используйте LaTeX для набора формулы

Источник

Расписание ЕГЭ−2023

Дата	ЕГЭ
Досрочный этап
20 марта (пн)	география, литература
23 марта (чт)	русский язык
27 марта (пн)	профильная и базовая математики
30 марта (чт)	иностранные языки (за исключением раздела «Говорение»), биология, физика
3 апреля (пн)	иностранные языки (раздел «Говорение»)
6 апреля (чт)	обществознание, информатика и ИКТ
10 апреля (пн)	история, химия
Основной этап
26 мая (пт)	география, литература, химия
29 мая (пн)	русский язык
1 июня (чт)	профильная и базовая математики
5 июня (пн)	история, физика
8 июня (чт)	обществознание
13 июня (вт)	иностранные языки (за исключением раздела «Говорение»), биология
16 июня (пт)	иностранные языки (раздел «Говорение»)
17 июня (сб)	иностранные языки (раздел «Говорение»)
19 июня (пн)	информатика и ИКТ
20 июня (вт)	информатика и ИКТ
22 июня (чт)	резерв: русский язык
23 июня (пт)	резерв: география, литература, иностранные языки (раздел «Говорение»)
26 июня (пн)	резерв: профильная и базовая математики
27 июня (вт)	резерв: иностранные языки (за исключением раздела «Говорение»), биология, информатика и ИКТ
28 июня (ср)	резерв: обществознание, химия
29 июня (чт)	резерв: история, физика
1 июля (сб)	резерв: по всем учебным предметам

Источник

Средний тестовый балл участников профильного экзамена ЕГЭ 2022 г. повысился в сравнении с предыдущими годами и составил 56,9. Также следует отметить заметный рост доли участников, показавших результат в интервале 61–80, то есть основного контингента IT, инженерных, естественно-научных специальностей вузов. Эта важная группа и обеспечила рост среднего тестового балла в 2022 г.

Более подробные аналитические и методические материалы ЕГЭ 2022 года доступны по ссылке.

ПЛАН ЭКЗАМЕНАЦИОННОЙ РАБОТЫ ЕГЭ ПО МАТЕМАТИКЕ 2023 ГОДА

читать полностью: спецификация.

Заданий базового уровня сложности 6, повышенного — 10, высокого — 2.
Работа рассчитана на 235 минут.

Обозначение уровня сложности задания: Б — базовый, П — повышенный, В — высокий.

Проверяемые требования (умения)	Уровень сложности задания	Максимальный балл за выполнение задания	Примерное время выполнения задания (мин.) базовый уровень / профильный уровень
Задание 1. Уметь выполнять действия с геометрическими фигурами, координатами и векторами	Б	1	5	3
Задание 2. Уметь выполнять действия с геометрическими фигурами, координатами и векторами	Б	1	10	3
Задание 3. Уметь строить и исследовать простейшие математические модели	Б	1	5	2
Задание 4. Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни	Б	1	15	8
Задание 5. Уметь решать уравнения и неравенства	Б	1	5	2
Задание 6. Уметь выполнять вычисления и преобразования	Б	1	5	3
Задание 7. Уметь выполнять действия с функциями	Б	1	10	4
Задание 8. Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни	П	1	15	6
Задание 9. Уметь строить и исследовать простейшие математические модели	П	1	15	7
Задание 10. Уметь выполнять действия с функциями	П	1	15	8
Задание 11. Уметь выполнять действия с функциями	П	1	15	9
Задание 12. Уметь решать уравнения и неравенства	П	2	20	10
Задание 13. Уметь выполнять действия геометрическими фигурами, координатами и векторами	П	3	40	20
Задание 14. Уметь решать уравнения и неравенства	П	2	30	15
Задание 15. Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни	П	2	30	25
Задание 16. Уметь выполнять действия с геометрическими фигурами, координатами и векторами	П	3		35
Задание 17. Уметь решать уравнения и неравенства	В	4		35
Задание 18. Уметь строить и исследовать простейшие математические модели	В	4		40

ОФИЦИАЛЬНАЯ ШКАЛА 2022 ГОДА

Первичный балл

Тестовый балл

Соответствие между минимальными первичными баллами и минимальными тестовыми баллами 2022 года. Распоряжение о внесении изменений в приложение № 2 к распоряжению Федеральной службы по надзору в сфере образования и науки. Перейти.

ПОРОГОВЫЕ БАЛЛЫ

Для получения аттестата: 27 тестовых (5 первичных) баллов. См. распоряжение Рособрнадзора.

Для поступления в вузы, подведомственные Министерству науки и высшей школы: 39 тестовых баллов. См. приказ Миннауки.

Для поступления в вузы, подведомственные Министерству просвещения: 39 тестовых баллов. См. приказ Минпроса.

ЭКЗАМЕНАЦИОННЫЕ БЛАНКИ

Правила заполнения бланков государственной итоговой аттестации. Скачать бланки в высоком качестве можно по ссылке.

ЧТО МОЖНО ВЗЯТЬ С СОБОЙ НА ЭКЗАМЕН

На экзамене по математике разрешается пользоваться линейкой, которая не содержит справочную информацию, для построения чертежей и рисунков. Источник.

Задания базовой части ЕГЭ по математике взяты из открытого банка экзаменационных заданий (http://mathege.ru) и представляют собой модельные задачи, на основе которых путем изменения конкретных числовых данных составляются реальные экзаменационные работы ЕГЭ. Задания повышенного и высокого уровня сложности были специально составлены для портала «РЕШУ ЕГЭ» или предлагались в официальных сборниках для подготовки к экзамену.

Авторы задач для подготовки к ЕГЭ:
И. Р. Высоцкий, Д. Д. Гущин, П. И. Захаров,
Р. К. Гордин,
А. В. Малышев,
С. В. Панферов, М. А. Посицельская, С. Е. Посицельский,
М. Я. Пратусевич,
С. Е. Рукшин,
А. В. Семенов, А. Л. Семенов, И. Н. Сергеев,
К. М. Столбов,
В. А. Смирнов,
С. А. Шестаков, Д. Э. Шноль, И. В. Ященко;
материалы сайта http://ege.yandex.ru.

Источник

4. Введение в теорию вероятностей

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Сложные задачи по теории вероятности

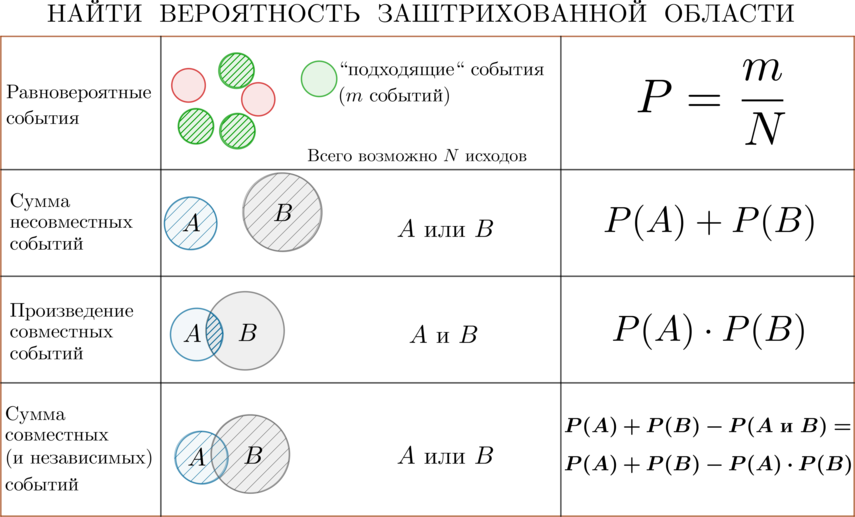
Общая памятка по всем разделам теории вероятностей:

Задание
1

#3858

Уровень задания: Равен ЕГЭ

Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы (4) очка в двух играх. Если команда выигрывает, она получает (3) очка, в случае ничьей — (1) очко, если проигрывает — (0) очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны (0,3).

Чтобы команда в двух играх набрала не менее (4) очков, ей нужно: либо 1) выиграть обе игры, либо 2) выиграть в одной из игр и сыграть вничью в другой игре.
Так как вероятности выиграть и проиграть одинакова и равна (0,3), то вероятность сыграть вничью равна (1-0,3-0,3=0,4).
Следовательно, вероятности в этих случаях равны соответственно:
1) (0,3cdot 0,3)
2) (0,3cdot 0,4+0,4cdot 0,3) (выиграть в первой игре и сыграть вничью во второй или сыграть вничью в первой и выиграть во второй).
Следовательно, вероятность того, что команда выйдет в следующий круг соревнований, равна [0,3cdot 0,3+0,3cdot 0,4+0,4cdot 0,3=0,33]

Ответ: 0,33

Задание
2

#2739

Уровень задания: Сложнее ЕГЭ

Илья решает задачу по геометрии, в которой дан четырёхугольник (ABCD), причём (AB = 5), (BC = 6), (CD = 4), (AD = 10). В условии задачи сказано, что одна из вершин является центром некоторой окружности и Илья думает, какую вершину ему выбрать в качестве центра этой самой окружности.

Известно, что вероятность выбора каждой конкретной вершины пропорциональна сумме длин сторон четырёхугольника (ABCD), проходящих через эту вершину. Какова вероятность того, что Илья выберет вершину (B)?

Через вершину (A) проходят стороны (AB) и (AD), их сумма: (AB + AD = 15).

Через вершину (B) проходят стороны (AB) и (BC), их сумма: (AB + BC = 11).

Через вершину (C) проходят стороны (BC) и (CD), их сумма: (BC + CD = 10).

Через вершину (D) проходят стороны (CD) и (DA), их сумма: (CD + DA = 14).

Обозначим вероятность выбора вершины (A) через (P(A)) (для остальных вершин аналогично). Тогда по условию имеем: [P(A) = 15k,qquad P(B) = 11k,qquad P(C) = 10k,qquad P(D) = 14k,,] но (P(A) + P(B) + P(C) + P(D) = 1), тогда (k = 0,02), откуда находим: (P(B) = 0,22).

Ответ: 0,22

Задание
3

#191

Уровень задания: Сложнее ЕГЭ

Монетку подбросили 10 раз. Какова вероятность того, что выпало не менее 9 орлов? Ответ округлите до тысячных.

Условие того, что выпало не менее 9 орлов эквивалентно тому, что выпало не более 1 решки, то есть либо ровно 1 решка, либо 0 решек.

Количество всевозможных различных исходов в серии из 10 испытаний равно (2^{10} = 1024).

Среди них есть 11 исходов, подходящих под условие: (Орёл; Орёл; …; Орёл), (Орёл; Орёл; …; Орёл; Решка), (Орёл; Орёл; …; Решка; Орёл), …, (Решка; Орёл; …; Орёл), следовательно, искомая вероятность равна [dfrac{11}{1024}.] После округления получим (0,011).

Ответ: 0,011

Задание
4

#190

Уровень задания: Сложнее ЕГЭ

Монетку подбросили 3 раза. Какова вероятность того, что выпало не менее 3 орлов? Ответ округлите до тысячных.

Условие того, что выпало не менее 3 орлов эквивалентно тому, что выпали только орлы.

Количество всевозможных различных исходов в серии из 3 испытаний равно (2^3 = . Среди них есть ровно один исход, подходящий под условие: (Орёл; Орёл; Орёл). Таким образом, искомая вероятность равна [dfrac{1}{8} = 0,125.]

Ответ: 0,125

Задание
5

#189

Уровень задания: Сложнее ЕГЭ

Монетку подбросили 2 раза. Какова вероятность того, что выпало не менее 1 орла? Ответ округлите до тысячных.

Всевозможных исходов в серии из 2 подбрасываний может быть (2^2 = 4): (Орёл; Орёл), (Орёл; Решка), (Решка; Орёл), (Решка; Решка).

Среди выписанных (всевозможных) исходов под условие задачи подходят первые 3, следовательно, искомая вероятность равна [dfrac{3}{4} = 0,75.]

Ответ: 0,75

Задание
6

#2658

Уровень задания: Сложнее ЕГЭ

Игорь трижды подбрасывает правильную игральную кость. Какова вероятность того, что за эти три подбрасывания ровно один раз выпадет число, кратное трём, а сумма результатов подбрасываний не будет делиться на (3)? Ответ округлите до сотых.

Так как игральная кость правильная, то вероятность выпадения каждой грани равна (dfrac{1}{6}). Среди чисел на гранях есть два числа, дающих при делении на (3) остаток (0), два числа, дающих при делении на (3) остаток (1) и два числа, дающих при делении на (3) остаток (2).

Тогда вероятность за одно подбрасывание получить, например, число, дающее при делении на (3) остаток (1), равна (dfrac{1}{3}). С другими остатками аналогично.

Условие задачи можно переформулировать в следующем виде: какова вероятность за три подбрасывания получить результаты, остатки от деления на (3) которых будут содержать единственный (0) и два одинаковых числа?

Таким образом, нас устраивают исходы, остатки от деления на (3) которых будут иметь вид:

[begin{aligned}
&0,quad 1,quad 1\
&1,quad 0,quad 1\
&1,quad 1,quad 0\
&0,quad 2,quad 2\
&2,quad 0,quad 2\
&2,quad 2,quad 0,.
end{aligned}]

Вероятность любого из выписанных исходов равна [dfrac{1}{3}cdot dfrac{1}{3}cdot dfrac{1}{3},.] При этом различных исходов здесь шесть, следовательно, вероятность получения подходящего исхода равна [6cdot dfrac{1}{3}cdot dfrac{1}{3}cdot dfrac{1}{3} = dfrac{2}{9},.] После округления получим ответ (0,22).

Ответ: 0,22

Задание
7

#2765

Уровень задания: Сложнее ЕГЭ

Таня заметила, что в казино “Подкинем” используют неправильную игральную кость (т.е. не у всех граней вероятности выпадения одинаковы). При этом она установила, что вероятность выпадения чётного числа равна (0,6); вероятность выпадения числа, делящегося на (3), равна (0,3); вероятность того, что выпадет (1) или (5), равна (0,22). Найдите вероятность того, что на этой игральной кости выпадет число (3). Ответ округлите до сотых.

Вероятность выпадения числа (n) обозначим через (P({n})), вероятность выпадения одного из чисел (m) и (n) обозначим через (P({m; n})), а вероятность выпадения одного из чисел (m), (n) и (k) обозначим через (P({m; n; k})). Тогда [P({2; 4; 6}) = 0,6qquadLeftrightarrowqquad P({1; 3; 5}) = 1 — 0,6 = 0,4]

При этом (P({1; 5}) = 0,22), но ведь (P({1; 3; 5}) — P({1; 5}) = P({3})), следовательно, [P({3}) = 0,4 — 0,22 = 0,18,.]

Ответ: 0,18

Если выпускник готовится к сдаче ЕГЭ по математике профильного уровня, ему необходимо научиться решать задачи на применение теории вероятности повышенной сложности. Как показывает практика многих лет, такие задания являются обязательной частью программы аттестационного испытания. Поэтому если учащийся не до конца понимает принцип решения сложных задач на теорию вероятности, ему обязательно стоит вновь разобраться в данной теме.

Вместе с образовательным порталом «Школково» старшеклассники смогут качественно подготовиться к прохождению аттестационного испытания. Наш сайт позволит определить наиболее сложные темы и восполнить пробелы в знаниях. Опытные специалисты «Школково» подготовили весь необходимый материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли легко справиться с решением сложных задач ЕГЭ на теорию вероятности. Базовая информация по данной теме представлена в разделе «Теоретическая справка».

Чтобы попрактиковаться в выполнении сложных задач ЕГЭ по теории вероятности, школьники могут выполнить соответствующие упражнения. Простые и сложные задания, подобранные нашими специалистами, содержат подробные алгоритмы решения и правильные ответы. База заданий регулярно обновляется и дополняется.

Выполнять упражнения школьники из Москвы и других российских городов могут в онлайн-режиме. При необходимости задания по теории вероятности в ЕГЭ можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.