Задания
Версия для печати и копирования в MS Word
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
А) масса взрослого кита
Б) объём железнодорожного вагона
В) площадь волейбольной площадки
Г) ширина футбольного поля
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
1) 162 кв. м
2) 100 т
3) 120 м
4) 68 м
В таблице под каждой буквой укажите соответствующий номер.
Спрятать решение
Решение.
Масса взрослого кита равна 100 т, объём железнодорожного вагона равен 120 м площадь волейбольной площадки — 162 кв.м, ширина футбольного поля — 68 м. Таким образом, имеем: А — 2, Б — 3, В — 1, Г — 4.
Ответ: 2314.
а) Найдите наименьшее натуральное число, половина которого является точным квадратом, а третья часть – точным кубом.
б) Найдите наименьшее натуральное число, половина которого является точным кубом, а третья часть – точным квадратом.
в) Существует ли натуральное число, половина которого является точным квадратом, третья часть – точным кубом, а пятая часть – точной пятой степенью?
Спрятать решение
Решение.
Решение: а) Пусть Х-искомое число. Т. к. снс делится и на 2, и на 3, то
Х будет наименьшим, если где п; к натуральные числа.
Т. к. точный квадрат (1*), а
точный куб (2*), имеем: из(1*)
кратны 2,
а из (2*) кратны 3. Наименьшие п; к, удовлетворяющие (1*) и (2*):
а число
б)Аналогично (а) где п; к натуральные числа.
Т. к. точный куб (3*), а
точный квадрат (4*), имеем: из(3*)
кратны 3,
а из (4*) кратны 2. Наименьшие п; к, удовлетворяющие (3*) и (4*):
а число
в)Аналогично (а) и (б) где п; к; р натуральные числа.
Т. к. точный квадрат (5*), а
точный куб (6*) и
(7*) является пятой степенью числа, имеем: из(5*)
кратны 2;
из (6*) кратны 3, из (7*)
кратны 5. Наименьшие п; к; р рудовлетворяющие (5*); (6*) и (7*):
а число
Источник: А. Ларин: Тренировочный вариант № 123.
———-
Дублирует задание 511229.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | 2 |
| Верно получен один из следующих результатов:
— обоснованное решение п. а; — обоснованное решение п. б; — искомая оценка в п. в; — пример в п. в, обеспечивающий точность предыдущей оценки |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Егэ математика 511613
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 3 № 511613
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) масса взрослого кита
Б) объём железнодорожного вагона
В) площадь волейбольной площадки
Г) ширина футбольного поля
В таблице под каждой буквой укажите соответствующий номер.
Масса взрослого кита равна 100 т, объём железнодорожного вагона равен 120 м площадь волейбольной площадки — 162 кв. м, ширина футбольного поля — 68 м. Таким образом, имеем: А — 2, Б — 3, В — 1, Г — 4.
—>
Задание 3 № 511613
А масса взрослого кита.
Mathb-ege. sdamgia. ru
11.10.2018 21:09:14
2018-10-11 21:09:14
Источники:
Https://mathb-ege. sdamgia. ru/problem? id=511613
ЕГЭ–2022, математика базовый уровень: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Егэ математика 511613
Егэ математика 511613
Егэ математика 511613
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 3 № 511962
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
А) расстояние от Земли до Луны
Б) объём воды в Чёрном море
В) площадь территории России
1) 5,9726 · 10 24 кг
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Расстояние измеряется в километрах, объём воды измеряется в км 3 , площадь территории измеряется в кв. км, масса измеряется в кг. Получаем следующее соответствие: А — 3, Б — 4, В — 2, Г — 1.
—>
Задание 3 № 511962
Егэ математика 511613.
Mathb. reshuege. ru
18.12.2020 17:37:54
2020-12-18 17:37:54
Источники:
Https://mathb. reshuege. ru/test? pid=511962
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Егэ математика 511613
Егэ математика 511613
Егэ математика 511613
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задания Д19 C7 № 511613
А) Найдите наименьшее натуральное число, половина которого является точным квадратом, а третья часть – точным кубом.
Б) Найдите наименьшее натуральное число, половина которого является точным кубом, а третья часть – точным квадратом.
В) Существует ли натуральное число, половина которого является точным квадратом, третья часть – точным кубом, а пятая часть – точной пятой степенью?
Решение: а) Пусть Х-искомое число. Т. к. снс делится и на 2, и на 3, то
Х будет наименьшим, если где п; к натуральные числа.
Т. к. точный квадрат (1*), а
Точный куб (2*), имеем: из(1*) кратны 2,
А из (2*) кратны 3. Наименьшие п; к, удовлетворяющие (1*) и (2*):
Б)Аналогично (а) где п; к натуральные числа.
Т. к. точный куб (3*), а
Точный квадрат (4*), имеем: из(3*) кратны 3,
А из (4*) кратны 2. Наименьшие п; к, удовлетворяющие (3*) и (4*):
В)Аналогично (а) и (б) где п; к; р натуральные числа.
Т. к. точный квадрат (5*), а
Точный куб (6*) и (7*) является пятой степенью числа, имеем: из(5*) кратны 2;
Из (6*) кратны 3, из (7*) кратны 5. Наименьшие п; к; р рудовлетворяющие (5*); (6*) и (7*):
—>
Задания Д19 C7 № 511613
А из 2 кратны 3.
Ege. sdamgia. ru
16.03.2019 14:06:35
2019-03-16 14:06:35
Источники:
Https://ege. sdamgia. ru/problem? id=511613
Тренировочная работа №3 статград пробник ЕГЭ 2023 по математике 11 класс 12 тренировочных вариантов МА2210301-МА2210312 с ответами и решением базовый и профильный уровень (БАЗА И ПРОФИЛЬ). Официальная дата проведения работы: 28 февраля 2023 года.
Скачать ответы и решения для вариантов
Пробник ЕГЭ 2023 математика 11 класс статград база
Варианты профильного уровня ЕГЭ 2023 математика статград
Вариант МА2210301 и ответы
1. Каждый день во время конференции расходуется 60 пакетиков чая. Конференция длится 9 дней. В пачке чая 50 пакетиков. Какого наименьшего количества пачек чая хватит на все дни конференции?
2. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
3. В таблице показано расписание пригородных электропоездов по направлению Москва Курская – Крутое – Петушки. Владислав пришёл на станцию Москва Курская в 18:20 и хочет уехать в Петушки на электропоезде без пересадок. Найдите номер ближайшего электропоезда, который ему подходит.
5. В коробке вперемешку лежат чайные пакетики с чёрным и зелёным чаем, одинаковые на вид, причём пакетиков с чёрным чаем в 4 раза больше, чем пакетиков с зелёным. Найдите вероятность того, что случайно выбранный из этой коробки пакетик окажется пакетиком с чёрным чаем.
8. Некоторые учащиеся 10-х классов школы ходили в апреле на спектакль «Гроза». В мае некоторые десятиклассники пойдут на постановку по пьесе «Бесприданница», причём среди них не будет тех, кто ходил в апреле на спектакль «Гроза». Выберите утверждения, которые будут верны при указанных условиях независимо от того, кто из десятиклассников пойдёт на постановку по пьесе «Бесприданница».
- 1) Каждый учащийся 10-х классов, который не ходил на спектакль «Гроза», пойдёт на постановку по пьесе «Бесприданница».
- 2) Нет ни одного десятиклассника, который ходил на спектакль «Гроза» и пойдёт на постановку по пьесе «Бесприданница».
- 3) Среди учащихся 10-х классов этой школы, которые не пойдут на постановку по пьесе «Бесприданница», есть хотя бы один, который ходил на спектакль «Гроза».
- 4) Найдётся десятиклассник, который не ходил на спектакль «Гроза» и не пойдёт на постановку по пьесе «Бесприданница».
9. На фрагменте географической карты схематично изображены границы деревни Покровское и очертания озёр (площадь одной клетки равна одному гектару). Оцените приближённо площадь озера Малого. Ответ дайте в гектарах с округлением до целого значения.
10. Диагональ прямоугольного экрана ноутбука равна 40 см, а ширина экрана ― 32 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
11. Пирамида Снофру имеет форму правильной четырёхугольной пирамиды, сторона основания которой равна 220 м, а высота — 104 м. Сторона основания точной музейной копии этой пирамиды равна 55 см. Найдите высоту музейной копии. Ответ дайте в сантиметрах.
12. В треугольнике ABC проведена биссектриса AL, угол ALC равен 112° , угол ABC равен 106° . Найдите угол ACB . Ответ дайте в градусах.
13. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?
15. В школе мальчики составляют 55 % от числа всех учащихся. Сколько в этой школе мальчиков, если их на 50 человек больше, чем девочек?
19. Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили второе четырёхзначное число. Затем из исходного числа вычли второе и получили 3366. В ответе укажите какое-нибудь одно такое исходное число.
20. Имеется два сплава. Первый содержит 45 % никеля, второй — 5 % никеля. Из этих двух сплавов получили третий сплав, содержащий 15 % никеля. Масса первого сплава равна 40 кг. На сколько килограммов масса первого сплава была меньше массы второго?
21. Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 2, 3 и 18. Найдите периметр четвёртого прямоугольника.
Вариант МА2210305 и ответы
1. Для покраски 1 кв. м потолка требуется 230 г краски. Краска продаётся в банках по 2 кг. Какое наименьшее количество банок краски нужно для покраски потолка площадью 44 кв. м?
3. В таблице представлены налоговые ставки на автомобили в Москве с 1 января 2013 года. Какова налоговая ставка (в рублях за 1 л. с. в год) на автомобиль мощностью 115 л. с.?
5. Помещение освещается двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года обе лампы перегорят.
6. В таблице даны результаты олимпиад по русскому языку и биологии в 9 «А» классе. Похвальные грамоты дают тем школьникам, у кого суммарный балл по двум олимпиадам больше 110 или хотя бы по одному предмету набрано не меньше 60 баллов. Укажите номера учащихся 9 «А» класса, набравших меньше 60 баллов по русскому языку и получивших похвальные грамоты, без пробелов, запятых и других дополнительных символов.
7. На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D. В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
8. Некоторые учащиеся 10-х классов школы ходили в ноябре на оперу «Евгений Онегин». В марте некоторые десятиклассники пойдут на оперу «Руслан и Людмила», причём среди них не будет тех, кто ходил в ноябре на оперу «Евгений Онегин». Выберите утверждения, которые будут верны при указанных условиях независимо от того, кто из десятиклассников пойдёт на оперу «Руслан и Людмила».
- 1) Каждый учащийся 10-х классов, который не ходил на оперу «Евгений Онегин», пойдёт на оперу «Руслан и Людмила».
- 2) Нет ни одного десятиклассника, который ходил на оперу «Евгений Онегин» и пойдёт на оперу «Руслан и Людмила».
- 3) Найдётся десятиклассник, который не ходил на оперу «Евгений Онегин» и не пойдёт на оперу «Руслан и Людмила».
- 4) Среди учащихся 10-х классов этой школы, которые не пойдут на оперу «Руслан и Людмила», есть хотя бы один, который ходил на оперу «Евгений Онегин».
9. План местности разбит на клетки. Каждая клетка обозначает квадрат 1м×1м . Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
10. Пожарную лестницу длиной 10 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте находится верхний конец лестницы? Ответ дайте в метрах.
11. Прямолинейный участок трубы длиной 4 м, имеющей в сечении окружность, необходимо покрасить снаружи (торцы трубы открыты, их красить не нужно). Найдите площадь поверхности, которую необходимо покрасить, если внешний обхват трубы равен 19 см. Ответ дайте в квадратных сантиметрах.
12. В треугольнике ABC стороны AC и BC равны. Внешний угол при вершине B равен 146° . Найдите угол C. Ответ дайте в градусах.
13. Даны два шара радиусами 4 и 2. Во сколько раз объём большего шара больше объёма меньшего?
15. Число больных гриппом в школе уменьшилось за месяц в пять раз. На сколько процентов уменьшилось число больных гриппом?
19. Найдите пятизначное число, кратное 15, любые две соседние цифры которого отличаются на 3. В ответе укажите какое-нибудь одно такое число.
20. Теплоход, скорость которого в неподвижной воде равна 19 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 43 часа после отправления из него. Сколько километров проходит теплоход за весь рейс?
21. На кольцевой дороге расположены четыре бензоколонки: А, Б, В и Г. Расстояние между А и Б — 55 км, между А и В — 40 км, между В и Г — 40 км, между Г и А — 30 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей дуге). Найдите расстояние (в километрах) между Б и В.
Вариант МА2210309 и ответы
2. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту цилиндра.
3. В группе 16 человек, среди них — Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе.
4. Агрофирма закупает куриные яйца только в двух домашних хозяйствах. Известно, что 40 % яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
9. Пристани A и B расположены на озере, расстояние между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч больше прежней, сделав по пути остановку на 8 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
13. Основанием правильной пирамиды PABCD является квадрат ABCD . Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру. а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60° . б) Найдите площадь сечения пирамиды, если AB = 30.
15. По вкладу «А» банк в конце каждого года планирует увеличивать на 13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n , при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
16. В треугольнике ABC медианы AA1 , BB1 и CC1 пересекаются в точке M . Известно, что AC MB = 3 . а) Докажите, что треугольник ABC прямоугольный. б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22 .
18. У Ани есть 800 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 32 рубля, а маленький — 25 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять. а) Может ли Аня купить 24 конверта? б) Может ли Аня купить 29 конвертов? в) Какое наибольшее число конвертов может купить Аня?
Вариант МА2210311 и ответы
1. Найдите периметр прямоугольника, если его площадь равна 12, а отношение соседних сторон равно 1:3.
2. Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 78. Найдите площадь поверхности шара.
3. В магазине в среднем из 120 сумок 15 имеют скрытые дефекты. Найдите вероятность того, что выбранная в магазине сумка окажется со скрытыми дефектами.
4. Игральный кубик бросают дважды. Известно, что в сумме выпало 11 очков. Найдите вероятность того, что во второй раз выпало 5 очков.
9. Игорь и Паша, работая вместе, могут покрасить забор за 40 часов. Паша и Володя, работая вместе, могут покрасить этот же забор за 48 часов, а Володя и Игорь, работая вместе, — за 60 часов. За сколько часов мальчики покрасят забор, работая втроём?
13. Основанием правильной пирамиды PABCD является квадрат ABCD . Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру. а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60° . б) Найдите площадь сечения пирамиды, если AB = 24 .
15. По вкладу «А» банк в конце каждого года планирует увеличивать на 11 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 7 % в первый год и на целое число n процентов за второй год. Найдите наименьшее значение n , при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
16. В треугольнике ABC медианы AA1 , BB1 и CC1 пересекаются в точке M . Известно, что AC MB = 3 . а) Докажите, что треугольник ABC прямоугольный. б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 18.
18. У Ани есть 400 рублей. Ей нужно купить конверты (большие и маленькие). Большой конверт стоит 22 рубля, а маленький — 17 рублей. При этом число маленьких конвертов не должно отличаться от числа больших конвертов больше чем на пять. а) Может ли Аня купить 19 конвертов? б) Может ли Аня купить 23 конверта? в) Какое наибольшее число конвертов может купить Аня?
Работы статград по математике для 9 и 11 класса
Share the post «Математика 11 класс ЕГЭ 2023 статград база и профиль варианты и ответы с решением»
- VKontakte
Метки: ЕГЭ 2023заданияматематика 11 классответыстатградтренировочная работа
Вариант № 8349414
1. Задание 1 № 77387
Найдите значение выражения .
2. Задание 2 № 26742
Найдите значение выражения .
3. Задание 3 № 26620
Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 750 рублей после понижения цены на 10%?
4. Задание 4 № 506387
Площадь треугольника со сторонами
можно найти по формуле Герона
, где
. Найдите площадь треугольника со сторонами
.
5. Задание 5 № 26777
Найдите , если
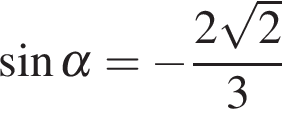
.
6. Задание 6 № 77356
Спидометр автомобиля показывает скорость в милях в час. Какую скорость (в милях в час) показывает спидометр, если автомобиль движется со скоростью 36 км в час? (Считайте, что 1 миля равна 1,6 км.)
7. Задание 7 № 26647
Найдите корень уравнения .
8. Задание 8 № 513733
Пол в комнате, имеющей форму прямоугольника со сторонами 4 м и 10 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 5 см и 20 см. Сколько потребуется таких дощечек?
9. Задание 9 № 511613
Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
|
ВЕЛИЧИНЫ |
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ |
|
|
А) масса взрослого кита Б) объём железнодорожного вагона В) площадь волейбольной площадки Г) ширина футбольного поля |
1) 162 кв. м 2) 100 т 3) 120 м 4) 68 м |
В таблице под каждой буквой укажите соответствующий номер.
10. Задание 10 № 285925
Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
11. Задание 11 № 27528
На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней выпадало более 2 миллиметров осадков.

12. Задание 12 № 77363
Вася загружает на свой компьютер из Интернета файл размером 30 Мб за 28 секунд. Петя загружает файл размером 28 Мб за 24 секунды, а Миша загружает файл размером 38 Мб за 32 секунды. Сколько секунд будет загружаться файл размером 665 Мб на компьютер с наибольшей скоростью загрузки?
13. Задание 13 № 506888
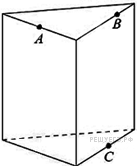
и
разбивает правильную треугольную призму на два многогранника. Сколько вершин у многогранника, у которого меньше граней?
14. Задание 14 № 514393
На рисунках изображены графики функций и касательные, проведённые к ним в точках с абсциссой x0. Установите соответствие между графиками функций и значениями производной этих функций в точке x0.
ГРАФИКИ
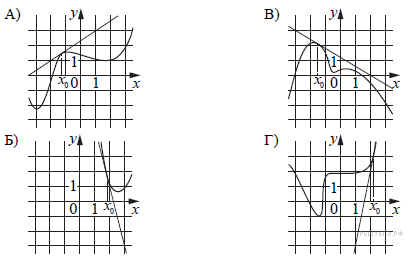
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
1.
2.
3.
4.
В таблице под каждой буквой укажите соответствующий номер.
|
A |
Б |
В |
Г |
15. Задание 15 № 509660
Найдите вписанный угол, опирающийся на дугу, длина которой равна длины окружности. Ответ дайте в градусах.
16. Задание 16 № 515747
В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра CD, CB и диагональ CD1 боковой грани равны соответственно 2, 4 и Найдите площадь поверхности параллелепипеда ABCDA1B1C1D1.
17. Задание 17 № 509782
Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
|
А) Б) В) Г) |
1) 2) 3) 4) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
А |
Б |
В |
Г |
18. Задание 18 № 510249
Некоторые сотрудники фирмы летом 2014 года отдыхали на даче, а некоторые — на море. Все сотрудники, которые не отдыхали на море, отдыхали на даче. Выберите утверждения, которые верны при указанных условиях.
1) Каждый сотрудник этой фирмы отдыхал летом 2014 года или на даче, или на море, или и там, и там.
2) Сотрудник этой фирмы, который летом 2014 года не отдыхал на море, не отдыхал и на даче.
3) Если Фаина не отдыхала летом 2014 года ни на даче, ни на море, то она является сотрудником этой фирмы.
4) Если сотрудник этой фирмы не отдыхал на море летом 2014 года, то он отдыхал на даче.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
19. Задание 19 № 508420
Найдите трехзначное натуральное число, большее 600, которое при делении на 4, на 5 и на 6 дает в остатке 3, и цифры которого расположены в порядке убывания слева направо. В ответе укажите какое-нибудь одно такое число.
20. Задание 20 № 506423
В обменном пункте можно совершить одну из двух операций:
1) за 3 золотых монеты получить 4 серебряных и одну медную;
2) за 6 серебряных монет получить 4 золотых и одну медную.
У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 35 медных. На сколько уменьшилось количество серебряных монет у Николы?
Задание 2. Информатика. Апробация 10.03.2023
Миша заполнял таблицу истинности логической функции (F)
$$
(x to neg (y to z)) lor w,
$$
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных (w), (x), (y), (z).
| F | ||||
| 0 | 0 | 0 | ||
| 1 | 0 | |||
| 0 | 1 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных (w), (x), (y), (z).
В ответе напишите буквы (w), (x), (y), (z) в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Функция (F) задана выражением ( neg x lor y), зависящим от двух переменных, а фрагмент таблицы имеет следующий вид:
В этом случае первому столбцу соответствует переменная (y), а второму — переменная (x). В ответе следует написать: (yx).
Решение:
Python
from itertools import permutations, product
def F(x, y, z, w):
return (x <= (not y <= z)) or w
for perm in permutations('xyzw'):
for a,b,c,d,e,f,g in product([0,1], repeat=7):
table = [[a,0,b,0,0],
[1,c,d,e,0],
[0,1,f,g,0]]
if table[0] == table[1]:
continue
if all(F(**dict(zip(perm,row))) == row[-1] for row in table):
print(*perm)
Ответ: (yzxw)
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-14

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!











