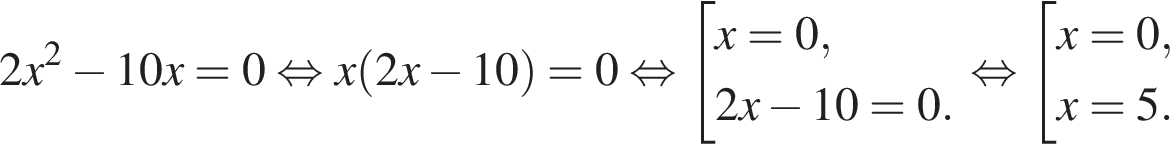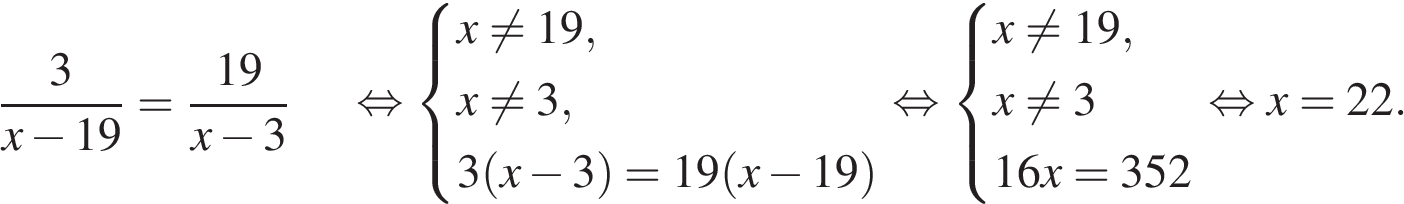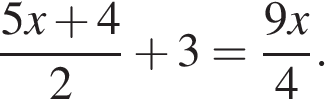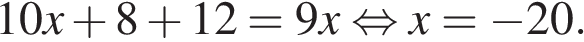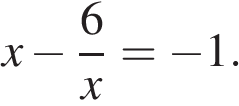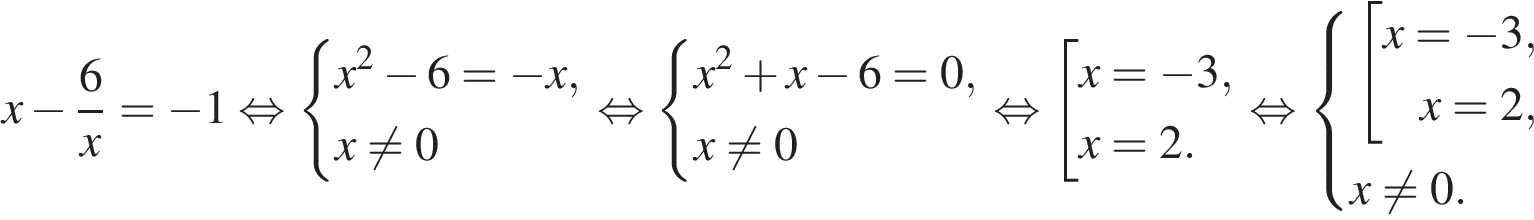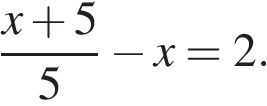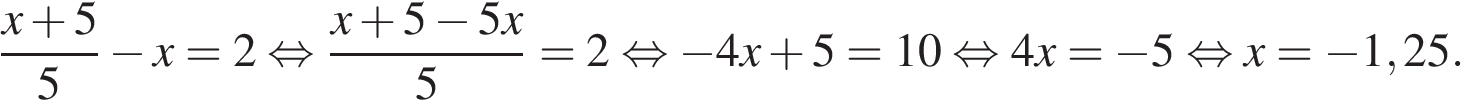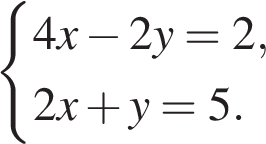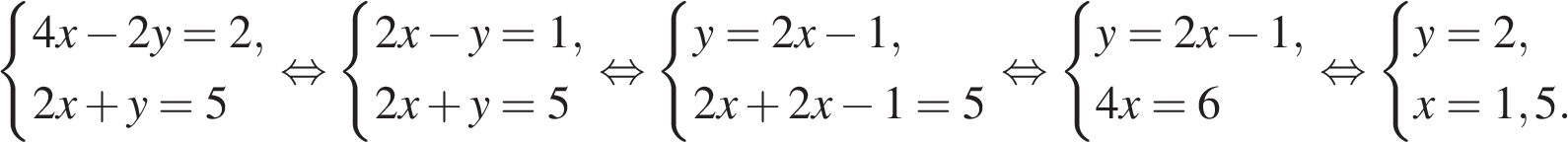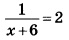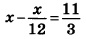Задания
Версия для печати и копирования в MS Word
Тип 7 № 27485
Прямая параллельна касательной к графику функции
Найдите абсциссу точки касания.
Спрятать решение
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой их угловые коэффициенты равны. Поэтому абсцисса точки касания находится из уравнения
:
Ответ: 0,5.
Аналоги к заданию № 27485: 6007 6037 6041 517174 517212 561169 561221 6009 6011 6013 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 4.1.1 Понятие о производной функции, геометрический смысл производной, 4.1.3 Уравнение касательной к графику функции, 4.2.1 Применение производной к исследованию функций и построению графиков
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2013-04-10

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Подборка по базе: Творческие задания социальная педагогика (3).pdf, Письменные задания для практических занятий.pdf, 11кл Олимпиадные задания по биологии.doc, 10 класс сайты для подготовки по АЛГЕБРЕ.docx, Письменные задания (1).docx, Практические задания к теме 3 (доработанное).docx, Учебные задания проверяемые вручную.docx, Пример 6 задания.docx, Практические задания.docx, Практическое занятие 11. Задания 2-4, 6-7_ просмотр попытки.pdf
1. Тип 7 № 119975
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
2. Тип 7 №
119976
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
3. Тип 7 №
119977
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени
с.
4. Тип 7 №
119978
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 3 м/с?
5. Тип 7 №
119979
Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 2 м/с?
6. Тип 7 №
501059

Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).
1. Тип 7 №
27489

2. Тип 7 №
27501

3. Тип 7 №
27503

4. Тип 7 №
510384

5. Тип 7 №
510403

6. Тип 7 №
510938

7. Тип 7 №
27504
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
8. Тип 7 №
27505
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
9. Тип 7 №
27506
На рисунке изображён график функции и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
10. Тип 7 №
40129
На рисунке изображен график функции y = f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите
11. Тип 7 №
40130
На рисунке изображен график производной функции Найдите абсциссу точки, в которой касательная к графику
параллельна прямой
или совпадает с ней.
12. Тип 7 №
40131
На рисунке изображен график производной функции Найдите абсциссу точки, в которой касательная к графику
параллельна оси абсцисс или совпадает с ней.
13. Тип 7 №
27485
Прямая параллельна касательной к графику функции
Найдите абсциссу точки касания.
14. Тип 7 №
27486
Прямая является касательной к графику функции
Найдите абсциссу точки касания.
15. Тип 7 №
119972
Прямая y = 3x + 1 является касательной к графику функции ax2 + 2x + 3. Найдите a.
16. Тип 7 №
119974
Прямая является касательной к графику функции
Найдите
17. Тип 7 №
119973
Прямая является касательной к графику функции
Найдите b, учитывая, что абсцисса точки касания больше 0.
18. Тип 7 №
515183
На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 6x или совпадает с ней.
19. Тип 7 №
525688
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Найдите значение производной функции g(x) = 6f(x) − 3x в точке x0.
20. Тип 7 №
525689
На рисунке изображены график функции и касательная к этому графику, проведённая в точке
Найдите значение производной функции
в точке x0.
21. Тип 7 №
525690

На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. Найдите значение производной функции
в точке x0.
22. Тип 7 №
525691
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. Найдите значение функции
в точке x0.
23. Тип 7 №
525698
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. Найдите значение производной функции
в точке x0.
24. Тип 7 №
525699
На рисунке изображены график функции и касательная к этому графику, проведённая в точке x0. Найдите значение производной функции
в точке x0.
Задание 2. Информатика. Апробация 10.03.2023
Миша заполнял таблицу истинности логической функции (F)
$$
(x to neg (y to z)) lor w,
$$
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных (w), (x), (y), (z).
| F | ||||
| 0 | 0 | 0 | ||
| 1 | 0 | |||
| 0 | 1 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных (w), (x), (y), (z).
В ответе напишите буквы (w), (x), (y), (z) в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Функция (F) задана выражением ( neg x lor y), зависящим от двух переменных, а фрагмент таблицы имеет следующий вид:
В этом случае первому столбцу соответствует переменная (y), а второму — переменная (x). В ответе следует написать: (yx).
Решение:
Python
from itertools import permutations, product
def F(x, y, z, w):
return (x <= (not y <= z)) or w
for perm in permutations('xyzw'):
for a,b,c,d,e,f,g in product([0,1], repeat=7):
table = [[a,0,b,0,0],
[1,c,d,e,0],
[0,1,f,g,0]]
if table[0] == table[1]:
continue
if all(F(**dict(zip(perm,row))) == row[-1] for row in table):
print(*perm)
Ответ: (yzxw)
9
задание
ПРОФИЛЬ
ЕГЭ математика
1
вариант
1. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите корень уравнения
2.
На рисунке изображён график функции вида где числа a, b и c — целые.
Найдите абсциссу вершины параболы.
3. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
4. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение x, при котором
5. 
изображён график функции вида где
числа a, b и c — целые. Найдите
6. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
7. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
8. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
9. 
изображён график функции вида где
числа a, b и c — целые. Найдите b.
10. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
9
задание
ПРОФИЛЬ
ЕГЭ математика
2
вариант
1. 
изображён график функции вида где
числа a, b и c — целые. Найдите значение .
2. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
3. 
изображён график функции вида где
числа a, b и c — целые. Найдите c.
4. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
5. 
изображён график функции вида где
числа a, b и c — целые. Найдите
6. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
7. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение дискриминанта уравнения .
8. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
9.
На рисунке изображён график функции вида где
числа a, b и c — целые. Найдите
10. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
9
задание
ПРОФИЛЬ
ЕГЭ математика
3
вариант
1. 
функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
2. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
3. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение дискриминанта уравнения .
4. 
изображён график функции вида где
числа a, b и c — целые. Найдите
5. 
изображён график функции вида где
числа a, b и c — целые. Найдите b.
6. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
7. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
8. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
9. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
10. 
изображён график функции вида где
числа a, b и c — целые. Найдите b.
9
задание
ПРОФИЛЬ
ЕГЭ математика
4
вариант
1. 
изображён график функции вида где
числа a, b и c — целые. Найдите c.
2. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
3. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение .
4. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
5. 
изображён график функции вида где
числа a, b и c — целые. Найдите
6.
На рисунке изображён график функции вида где числа a, b и c — целые.
Найдите абсциссу вершины параболы.
7. 
изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
8. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите
9. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение дискриминанта уравнения .
10. 
изображён график функции вида где
числа a, b и c — целые. Найдите
значение x, при котором
Ответы
9
задание
ПРОФИЛЬ
ЕГЭ математика
1
вариант
|
№ п/п |
№ задания |
Ответ |
|
1 |
563824 |
1 |
|
2 |
564655 |
4 |
|
3 |
564586 |
2,5 |
|
4 |
564974 |
2,75 |
|
5 |
564208 |
-2,25 |
|
6 |
564160 |
2 |
|
7 |
562285 |
19 |
|
8 |
562157 |
-7 |
|
9 |
564971 |
11 |
|
10 |
564195 |
2,5 |
9
задание
ПРОФИЛЬ
ЕГЭ математика
2
вариант
|
№ п/п |
№ задания |
Ответ |
|
1 |
562153 |
-4,25 |
|
2 |
564189 |
2 |
|
3 |
564967 |
-5 |
|
4 |
564578 |
1 |
|
5 |
564201 |
-3,625 |
|
6 |
564187 |
-0,5 |
|
7 |
562292 |
44 |
|
8 |
562158 |
9,875 |
|
9 |
564650 |
1,25 |
|
10 |
564554 |
0 |
9
задание
ПРОФИЛЬ
ЕГЭ математика
3 вариант
|
№ п/п |
№ задания |
Ответ |
|
1 |
564187 |
-0,5 |
|
2 |
564586 |
2,5 |
|
3 |
562293 |
8 |
|
4 |
564210 |
-2,75 |
|
5 |
564969 |
-5 |
|
6 |
562282 |
4,75 |
|
7 |
564194 |
-2 |
|
8 |
562154 |
-34 |
|
9 |
564587 |
-0,5 |
|
10 |
564970 |
-13 |
9
задание
ПРОФИЛЬ
ЕГЭ математика
4
вариант
|
№ п/п |
№ задания |
Ответ |
|
1 |
564966 |
2 |
|
2 |
564184 |
2,5 |
|
3 |
562162 |
11 |
|
4 |
564554 |
0 |
|
5 |
564205 |
-1,6 |
|
6 |
564657 |
-4 |
|
7 |
564193 |
5 |
|
8 |
564585 |
2 |
|
9 |
562061 |
8 |
|
10 |
564972 |
-3 |
💡 Если Вы — учитель математики, то Вы можете создавать готовые карточки для учеников с индивидуальными заданиями и с ответами для отработки заданий на графики функций. Данные задачи доступны в Конструкторе бесплатно.
|
3. На рисунке изображён график функции y=3x^2+bx+c . Найдите f(6) . [Ответ: 10] |
Смотреть видеоразбор похожего >> |
|
4. На рисунке изображён график функции y=ax^2+12x+c . Найдите f(7) . [Ответ: -74] |
Смотреть видеоразбор похожего >> |
|
5. На рисунке изображён график функции y=ax^2+bx+12 . Найдите f(-7) . [Ответ: 19] |
Смотреть видеоразбор похожего >> |
|
6. На рисунке изображён график функции y=ax^2+bx+c . Найдите f(1) . [Ответ: 49] |
Смотреть видеоразбор похожего >> |
|
7. На рисунке изображён график функции y=ax^2+bx+c , где числа a , b и c — целые. Найдите f(-5) . [Ответ: -29] |
Смотреть видеоразбор похожего >> |
|
8. На рисунке изображён график функции f(x)=frac{k}{x}+a . Найдите f(0.1) . [Ответ: -17] |
Смотреть видеоразбор похожего >> |
|
9. На рисунке изображён график функции f(x)=frac{k}{x}+a . Найдите, при каком значении x значение функции равно -4.4 . [Ответ: -12.5] |
Смотреть видеоразбор похожего >> |
|
10. На рисунке изображён график функции f(x)=frac{k}{x+a} . Найдите f(-3.5) . [Ответ: 6] |
Смотреть видеоразбор похожего >> |
|
11. На рисунке изображён график функции f(x)=frac{k}{x+a} . Найдите значение x , при котором f(x) = 10 . [Ответ: 0.6] |
Смотреть видеоразбор похожего >> |
|
12. На рисунке изображён график функции f(x)=frac{kx+a}{x+b} . Найдите k . [Ответ: 1] |
Смотреть видеоразбор похожего >> |
|
13. На рисунке изображён график функции f(x)=frac{kx+a}{x+b} . Найдите a . [Ответ: 2] |
Смотреть видеоразбор похожего >> |
|
14. На рисунке изображён график функции f(x)=b+log_ax . Найдите f(frac{1}{9}) . [Ответ: 3] |
Смотреть видеоразбор похожего >> |
|
15. На рисунке изображён график функции f(x)=b+log_ax . Найдите значение x , при котором f(x)=-11 . [Ответ: 64] |
Смотреть видеоразбор похожего >> |
|
16. На рисунке изображён график функции f(x)=log_a(x+b) . Найдите f(26) . [Ответ: -2] |
Смотреть видеоразбор похожего >> |
|
17. На рисунке изображён график функции f(x)=log_a(x+b) . Найдите значение x , при котором f(x)=4 . [Ответ: 82] |
Смотреть видеоразбор похожего >> |
|
18. На рисунке изображён график функции f(x) = a^x+b . Найдите f(-2) . [Ответ: 22] |
Смотреть видеоразбор похожего >> |
|
19. На рисунке изображён график функции f(x) = a^x+b . Найдите значение x , при котором f(x) = 77 . [Ответ: -4] |
Смотреть видеоразбор похожего >> |
|
20. На рисунке изображён график функции f(x) = a^{x+b} . Найдите f(4) . [Ответ: 9] |
Смотреть видеоразбор похожего >> |
|
21. На рисунке изображён график функции f(x) = a^{x+b} . Найдите значение x , при котором f(x) = 64 . [Ответ: 8] |
Смотреть видеоразбор похожего >> |
|
22. На рисунке изображён график функции f(x) = ksqrt{x} . Найдите f(8.41) . [Ответ: 8.7] |
Смотреть видеоразбор похожего >> |
|
23. На рисунке изображён график функции f(x) = ksqrt{x} . Найдите значение x , при котором f(x)=-6.75 . [Ответ: 7.29] |
Смотреть видеоразбор похожего >> |
|
24. На рисунке изображены графики функций f(x)=-4x+22 и g(x)=ax^2+bx+c , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: 9] |
Смотреть видеоразбор похожего >> |
|
25. На рисунке изображены графики функций f(x)=-6x-28 и g(x)=ax^2+bx+c , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: 38] |
Смотреть видеоразбор похожего >> |
|
26. На рисунке изображены графики функций f(x)=frac{k}{x} и g(x)=ax+b , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: 0.2] |
Смотреть видеоразбор похожего >> |
|
27. На рисунке изображены графики функций f(x)=frac{k}{x} и g(x)=ax+b , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: 20] |
Смотреть видеоразбор похожего >> |
|
28. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков. [Ответ: -2.08] |
Смотреть видеоразбор похожего >> |
|
29. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков. [Ответ: -2.4] |
Смотреть видеоразбор похожего >> |
|
30. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков. [Ответ: -11.3] |
Смотреть видеоразбор похожего >> |
|
31. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков. [Ответ: 6.8] |
Смотреть видеоразбор похожего >> |
|
32. На рисунке изображены графики функций f(x) = 2x^2+16x+30 и g(x) = ax^2+bx+c , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: -9] |
Смотреть видеоразбор похожего >> |
|
33. На рисунке изображены графики функций f(x) = -2x^2-3x+1 и g(x) = ax^2+bx+c , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: -13] |
Смотреть видеоразбор похожего >> |
|
34. На рисунке изображены графики функций f(x)=asqrt{x} и g(x)=kx+b , которые пересекаются в точке A. Найдите абсциссу точки A. [Ответ: 3.24] |
Смотреть видеоразбор похожего >> |
|
35. На рисунке изображены графики функций f(x)=asqrt{x} и g(x)=kx+b , которые пересекаются в точке A. Найдите ординату точки A. [Ответ: 9] |
Смотреть видеоразбор похожего >> |
|
36. На рисунке изображён график функции f(x) = asin{x}+b . Найдите a . [Ответ: 2] |
Смотреть видеоразбор похожего >> |
|
37. На рисунке изображён график функции f(x) = asin{x}+b . Найдите b . [Ответ: 1,5] |
Смотреть видеоразбор похожего >> |
|
38. На рисунке изображён график функции f(x) = acos{x}+b . Найдите a . [Ответ: 1,5] |
Смотреть видеоразбор похожего >> |
|
39. На рисунке изображён график функции f(x) = acos{x}+b . Найдите b . [Ответ: −1] |
Смотреть видеоразбор похожего >> |
|
40. На рисунке изображён график функции f(x) = a;tg{x}+b . Найдите a . [Ответ: 2] |
Смотреть видеоразбор похожего >> |
|
41. На рисунке изображён график функции f(x) = a;tg{x}+b . Найдите b . [Ответ: −1,5] |
Смотреть видеоразбор похожего >> |
Решите систему уравнений В ответ запишите х + у.
Разделим обе части первого уравнения на 2 и решим систему методом подстановки:
Искомая сумма равна 3,5.
Систему можно было бы решить методом алгебраического сложения:
Решите систему уравнений В ответ запишите х + у.
Решим систему методом подстановки:
Искомая сумма равна 5.
Решите систему уравнений В ответ запишите х + у.
Решим систему методом подстановки:
Искомая сумма равна 3.
Решите систему уравнений В ответ запишите х + у.
Решим систему методом подстановки:
Искомая сумма равна −1.
Решите систему уравнений В ответ запишите х + у.
Решим систему методом подстановки:
Искомая сумма равна 5.
Решите систему уравнений В ответ запишите х + у.
Решим систему методом подстановки:
Искомая сумма равна 1.
Решите систему уравнений
Выразим переменную из второго уравнения и подставим в первое:
Решим первое уравнение системы. Пусть
Тогда
Система имеет четыре пары решений:
Ответ: (−1; −6); (1; 6); (−6; −1); (6; 1).
Решите систему уравнений
Преобразуем систему уравнений:
откуда получаем решения системы уравнений : (2; −1) и (2; 1).
откуда здесь получилось 22=11х? можно расписать подробнее?
Алина, домножили на два верхнюю часть и после этого сложили с нижней.
Решите систему уравнений
Выразим одну переменную через другую из второго уравнения и подставим полученное выражение в первое уравнение
Заметим, что пара корней не является корнями уравнения, потому что при
знаменатель второго уравнения обращается в ноль.
Приведем решение Анны Мечевой.
Заметим, что выражение обращается в 0 при x = 4 или y = 6. Подставим эти значения во второе уравнение.
Это уравнение не имеет решений.
Следовательно, решением уравнения является пара чисел (3, 6).
Решите систему уравнений
Из второго уравнения системы получаем Первое уравнение системы принимает вид
Уравнение x 2 = 1 имеет корни x = −1 и x = 1.
Уравнение x 2 = 9 имеет корни x = −3 и x = 3.
Значит, решение исходной системы: (−1; −3), (1; 3), (−3; −1) и (3; 1).
Ответ: (−1; −3), (1; 3), (−3; −1); (3; 1).
Аналоги к заданию № 338894: 341366 Все
Решите систему уравнений
Подставим во второе уравнение системы, получим уравнение относительно
. Отсюда
. Подставим
в уравнение
, получим:
Решите систему уравнений
Подставим во второе уравнение системы, получим уравнение относительно
. Отсюда
и
. Подставим
и
в уравнение
, получим:
и
соответственно.
Источник
Задание 9 номер 311315
Решите систему уравнений В ответ запишите х + у.
Решим систему методом подстановки:
Искомая сумма равна 5.
Найдите корни уравнения
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Запишем уравнение в виде:
По теореме Виета, сумма корней равна 5, а их произведение равно 4. Тем самым, это числа 4 и 1.
Решите уравнение .
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
По теореме, обратной теореме Виета, сумма корней равна 1, а их произведение −6.
Тем самым, это числа −2 и 3.
Решите уравнение
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Умножим обе части уравнения на
Решите систему уравнений
Выразим переменную y из одного уравнения и подставим во второе:
Андрей, спасибо, правка внесена.
Решите уравнение: .
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Используем свойство пропорции.
Найдите корни уравнения .
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решите уравнение:
Раскладывая на множители левую часть уравнения, получаем Таким образом, корни уравнения
Ответ:
а почему исчезло 24? никаких предпосылок для этого я не вижу
Гость, раскройте скобки.
Решите систему
Вычтем из первого уравнения второе, используем формулу разности квадратов, затем метод подстановки:
Ответ:
Решите систему уравнений
Ответ:
Решите уравнение
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Один из корней уравнения равен −1. Найдите второй корень.
Подставим известный корень в уравнение: . Получим уравнение относительно
. Решим его:
. Подставим
в уравнение:
, откуда
Ответ:
Источник
Задание 9 номер 311315
Решите систему уравнений В ответ запишите х + у.
Разделим обе части первого уравнения на 2 и решим систему методом подстановки:
Искомая сумма равна 3,5.
Систему можно было бы решить методом алгебраического сложения:
Решите систему уравнений В ответ запишите х + у.
Решим систему методом подстановки:
Искомая сумма равна 5.
Решите систему уравнений В ответ запишите х + у.
Решим систему методом подстановки:
Искомая сумма равна 3.
Решите систему уравнений В ответ запишите х + у.
Решим систему методом подстановки:
Искомая сумма равна −1.
Решите систему уравнений В ответ запишите х + у.
Решим систему методом подстановки:
Искомая сумма равна 5.
Решите систему уравнений В ответ запишите х + у.
Решим систему методом подстановки:
Искомая сумма равна 1.
Решите систему неравенств
На каком рисунке изображено множество её решений?
В ответе укажите номер правильного варианта.
Решением системы является отрезок, изображённый под номером 2.
Правильный ответ указан под номером 2.
Решите систему неравенств
На каком из рисунков изображено множество её решений?
В ответе укажите номер правильного варианта.
Правильный ответ указан под номером 3.
Решите систему неравенств
На каком рисунке изображено множество её решений?
В ответе укажите номер правильного варианта.
Решим систему неравенств:
Решение неравенства изображено под номером 4.
Решите систему неравенств
Решим первое неравенство системы:
Выражение всегда больше нуля поэтому данное неравенство эквивалентно неравенству
Решим второе неравенство:
Пересекая решения обоих неравенств, получим, что решением системы является отрезок
Ответ:
Можно сразу заметить, что в знаменателе первого выражения стоит квадрат числа плюс положительное число, значит, знаменатель всегда больше нуля.
Решите систему уравнений
Выразим переменную из второго уравнения и подставим в первое:
Решим первое уравнение системы. Пусть
Тогда
Система имеет четыре пары решений:
Ответ: (−1; −6); (1; 6); (−6; −1); (6; 1).
Решите систему уравнений
Преобразуем систему уравнений:
откуда получаем решения системы уравнений : (2; −1) и (2; 1).
откуда здесь получилось 22=11х? можно расписать подробнее?
Алина, домножили на два верхнюю часть и после этого сложили с нижней.
Решите систему неравенств
Используя тот факт, что знаменатель первого неравенства всегда больше нуля, преобразуем систему неравенств:
А куда делся знаменатель в первой части? Его можно просто так выкидывать?
Никита, знаменатель в первом уравнении всегда больше ноля, поэтому мы его не учитываем.
Решите систему неравенств
Преобразуем систему неравенств:
Аналоги к заданию № 338522: 341418 Все
Решите систему уравнений
Подставим во второе уравнение системы, получим уравнение относительно
. Отсюда
. Подставим
в уравнение
, получим:
Решите систему уравнений
Подставим во второе уравнение системы, получим уравнение относительно
. Отсюда
и
. Подставим
и
в уравнение
, получим:
и
соответственно.
Источник
Решение.
Последовательно получаем:
Ответ: 05
8. Задание 9 № 338180
Уравнение 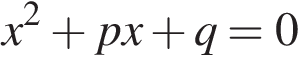
Решение.
По теореме Виета
Ответ: -24
9. Задание 9 № 338202
Квадратный трёхчлен разложен на множители: 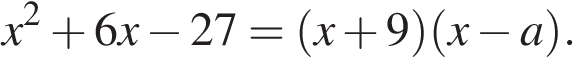
Решение.
Корни уравнения 
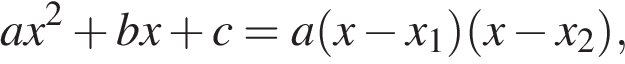
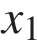
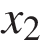

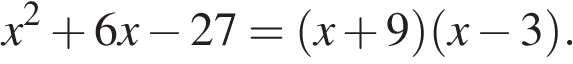
Ответ: 3
10. Задание 9 № 338526
Решите уравнение
Решение.
Квадраты чисел равны, если числа равны или противоположны:
Ответ: −2,5.
Приведем другое решение.
Раскроем скобки в обеих частях уравнения:
Приведем другое решение.
Воспользуемся формулой разности квадратов:
Ответ: -2,5
11. Задание 9 № 311381
Решите уравнение: 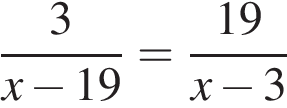
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение.
Используем свойство пропорции.
Ответ: 22
12. Задание 9 № 311755
Решите уравнение
Решение.
Умножим левую и правую часть уравнения на 4, получаем:
Ответ: -20
13. Задание 9 № 338503
Решите уравнение
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение.
Умножим обе части уравнения на
Ответ: -32
14. Задание 9 № 338805
Решите уравнение
Решение.
Последовательно получаем:
Ответ: -1,25
15. Задание 9 № 311315
Решите систему уравнений
В ответе запишите сумму компонентов решений системы.
Решение.
Разделим обе части первого уравнения на 2 и решим систему методом подстановки:
Ответ: 3,5.
Задание 9 353555 решите уравнение
Решите уравнение
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Умножим обе части уравнения на 4, используем формулу корней квадратного уравнения для четного коэффициента при х:
Заметим, что в решении использована формула корней квадратного уравнения с четным коэффициентом b:
где
В девятом задании модуля алгебра ОГЭ по математике нам предлагают решить уравнения. Это могут быть как линейные уравнения, которые решаются переносом всех известных членов в одну сторону, а неизвестных (x) в другую, так и квадратные уравнения, которые в свою очередь могут быть полными и неполными. Судя по материалам ОГЭ и практике проведения экзамена, наиболее вероятным заданием может быть решение линейного или квадратного уравнения. Тем не менее мы рассмотрим задания по всей этой тематике. Сложность заданий как всегда возрастает от задания к заданию. Ответом в задании №9 является целое число или конечная десятичная дробь.
Теория к заданию №9
Ниже я привел теорию по решениям линейных и квадратных уравнений:
Схема решения, правила и алгоритм действий при решении линейного уравнения:
Схема решения, правила и порядок действий при решении квадратного уравнения:
В трех типовых вариантах я разобрал данные случаи – в первом варианте вы найдете подробные указания по решению линейных уравнений, во втором разобран пример решения неполного квадратного уравнения, а в третьем – решение полного квадратного уравнения с вычислением дискриминанта.
Найдите корень уравнения:
Данное уравнение представляет собой обыкновенное уравнение первой степени и решается переносом всех известных частей в правую часть, оставив x слева.
Для начала следует раскрыть скобки: 10x – 90 = 7
Затем переносим 90 в правую часть (не забываем поменять знак):
Затем делим обе части на 10:
pазбирался: Даниил Романович | обсудить разбор | оценить
Это неполное квадратное уравнение, в котором не обязательно вычислять дискриминант, а достаточно вынести x за скобку:
Произведение множителей тогда равно нулю, когда один из множителей равен нолю:
Так как в ответе просят указать наименьший корень, то это -4.
pазбирался: Даниил Романович | обсудить разбор | оценить
Уравнение является полным квадратным уравнением, поэтому классическим вариантом решения является вычисление дискриминанта. Но в данном случае можно заметить, что все множители кратны двум, поэтому можно все уравнение разделить на 2 для удобства вычисления:
Далее вычисляем дискриминант:
x = (- b — √D) / 2a = (5 — 3 )/ 2 •4 = 0,25
x = (- b + √D) / 2a = (5 + 3 )/ 2 •4 = 1
Так как нам нужно выбрать меньший из корней по условию, то выбираем 0,25
pазбирался: Даниил Романович | обсудить разбор | оценить
В данной задаче нам предстоит решить линейное уравнение. Подход к решению таких уравнений достаточно простой – всё, что известно переносим в правую часть, всё, что неизвестно – оставляем в левой. Далее выполняем необходимое арифметическое действие.
Переносим 9 в правую часть (не забываем про смену знака):
7х = 40 + 9, что эквивалентно
х в нашем случае – это неизвестный множитель, следовательно, чтобы его найти, делим произведение на известный множитель:
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите корень уравнения:
режде всего, исключим
Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.
Далее решаем уравнение. Представляем число 2 в уравнении справа в виде дроби 2/1. Уравнение получает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Выполним умножение в левой части уравнения и раскроем скобки справа:
Поменяем местами левую и правую части уравнения, чтобы оно приняло привычный вид:
Переносим 12 из левой части в правую:
ОДЗ это значение не исключает, поэтому оно является искомым результатом.Ответ: -5,5
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите корень уравнения:
Обе части уравнения приводим к единому знаменателю 12: 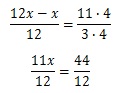
pазбирался: Даниил Романович | обсудить разбор | оценить
Имеем линейное уравнение:
Следовательно, начинаем решение с переноса слагаемых (с переменной влево, без переменной – вправо): 3х + 7х= – 5 – 2, не забывая изменять знак у слагаемых, которые переносим. Теперь приводим подобные в каждой части, получаем 10х= –7.
Находим неизвестный множитель делением произведения –7 на известный множитель 10, получаем –0,7.
Запись решения выглядит так:
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание 9 ОГЭ по математике. Уравнения, неравенства, системы уравнений и неравенств
При выполнении задания 9 ОГЭ по математике необходимо:
уметь решать линейные и квадратные уравнения, системы уравнений и неравенств.
Пример 1. Решите уравнение .
Решение. Уравнение линейное. Раскрываем скобки, приводим подобные слагаемые, все «иксы» переносим в левую часть равенства, всё без «иксов» – вправо:
Ответ: — 2.
Пример 2. Решите уравнение . Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение. Уравнение является квадратным , , . Вычисляем дискриминант и корни:
Ответ: .
Пример 3. Решите уравнение . Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Решение. В левой части данного уравнения произведение двух множителей-скобок, и это произведение равно нулю. Это возможно тогда и только тогда, когда хотя бы один из множителей равен нулю. Значит, получаем два уравнения:
Тогда меньший из корней уравнения равен -0,75.
Ответ: -0,75.
Пример 4. Решите систему уравнений
В ответе запишите значение .
Решение. Используем метод подстановки: из второго уравнения можно выразить y и подставить в первое уравнение.
Пример 5. На рисунке изображены графики функций и . Вычислите ординату точки B.
Решение. Для нахождения координат точек пересечения графиков заданных функций необходимо решить систему уравнений.
Найдём корни первого уравнения системы.
̶ абсцисса точка B.
Тогда ордината точки В:
Ответ: -5.
Пример 6. Найдите наибольшее значение x, удовлетворяющее системе неравенств:
Решение. Выразим из каждого неравенства переменную x. Не забываем, что при делении обеих частей неравенства на положительное число знак неравенства не меняется, при делении на отрицательное число ̶ знак неравенства меняется на противоположный.
Используем числовую прямую. Решение первого неравенства отметим штриховкой («ёлочкой») с наклоном вправо, второго неравенства ̶ штриховкой с наклоном влево. При этом точка -2 будет «закрашенной», т.к. знак первого неравенства нестрогий, а точка -5,5 будет «выколотой», т.к. знак второго неравенства строгий.
Решением системы неравенств является тот промежуток, на котором пересеклись две «ёлочки», то есть две штриховки. Это промежуток . «Выколотой» точке соответствует круглая скобка, «закрашенной» ̶ квадратная.
Ответим на вопрос задачи. Наибольшее значение
источники:
http://spadilo.ru/zadaniye-9-oge-po-matematike/
http://ege-study.ru/zadanie-9-oge-po-matematike-uravneniya-neravenstva-sistemy-uravnenij-i-nera-venstv/
Вещественное
шестизначное
число 562154
.
23 — сумма цифр числа.
Число имеет следующие делители: 1, 2, 31, 62, 9067, 18134, 281077, 562154.
870528 — сумма делителей числа.
562154 и 0.000001778871981698965 — обратные числа.
Другие системы счисления:
двоичный вид числа: 10001001001111101010, троичный вид числа: 1001120010112, восьмеричный вид числа: 2111752, шестнадцатеричный вид числа: 893EA.
Количество информации в числе байт 562154 — 548 килобайтов 1002 байта .
Азбука Морзе для числа: ….. -…. ..— .—- ….. ….-
Число — не число Фибоначчи.
Синус числа: -0.5245, косинус числа: -0.8514, тангенс числа: 0.6161.
Логарифм натуральный числа равен 13.2395.
Десятичный логарифм числа: 5.7499.
749.7693 это квадратный корень из числа 562154, 82.5313 — кубический.
Возведение числа в квадрат: 3.1602e+11.
Число секунд 562154 представляет из себя 6 дней 12 часов 9 минут 14 секунд .
Нумерологическое цифра числа 562154 — 5.
Задание 9 562154 егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 9 № 562153
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите значение.
Уравнение параболы с вершиной в точке с координатами имеет вид По графику видно, что при смещении от вершины на 2 клетки вправо (или влево) график смещается на 1 клетку вниз, поэтому старший коэффициент Вершина параболы находится в точке (6; 8), следовательно, уравнение параболы имеет вид
—>
Задание 9 № 562153
За пи сы вай тесь на бес плат ное за ня тие.
Ege. sdamgia. ru
18.09.2018 14:59:34
2018-09-18 14:59:34
Источники:
Https://ege. sdamgia. ru/problem? id=562153
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Задание 9 562154 егэ математика
Задание 9 562154 егэ математика
Задание 9 562154 егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите значение.
—>
На рисунке изображён график функции вида где числа a, b и c целые.
Math-ege. sdamgia. ru
25.11.2020 11:28:14
2020-11-25 11:28:14
Источники:
Https://math-ege. sdamgia. ru/test? id=44327255
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Задание 9 562154 егэ математика
Задание 9 562154 егэ математика
Задание 9 562154 егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 9 № 509253
На рисунке изображены графики функций и которые пересекаются в точках A и B. Найдите абсциссу точки B.
График функции должен пересекать ось ординат в точке Значит, график изображен синим цветом, а график — оранжевым. По рисунку определяем, что G(−3) = 2, G(−1) = −2, G(2) = 7. Тогда
Решая полученную систему, получаем: A = 1, B = 2, из G(2) = 7 получим C = −1. Теперь найдём абсциссу точки B:
Таким образом, ответ — 7.
Задание 9 № 562060
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите значение.
По рисунку определяем, что значит,
Задание 9 № 562061
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите значение дискриминанта уравнения.
По рисунку определяем, что
Дискриминант уравнения равен
Неоднозначное задание. Равносильные уравнения могут иметь разные дискриминанты. Вот пример: у уравнения дискриминант равен 25, а у уравнения дискриминант равен 100.
Действительно, умножение обеих частей уравнения на отличное от нуля приводит к другому уравнению, хоть и с теми же корнями. Если коэффициенты исходного и полученного уравнений квадратных уравнений отличаются в K раз, то их дискриминанты отличаются в K 2 раз. Но вопрос поставлен про конкретное уравнение, поэтому неоднозначности нет.
Задание 9 № 562153
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите значение.
Уравнение параболы с вершиной в точке с координатами имеет вид По графику видно, что при смещении от вершины на 2 клетки вправо (или влево) график смещается на 1 клетку вниз, поэтому старший коэффициент Вершина параболы находится в точке (6; 8), следовательно, уравнение параболы имеет вид
Задание 9 № 562153
Задание 9 № 562061
Задание 9 562061.
Math-ege. sdamgia. ru
21.02.2019 7:56:54
2019-02-21 07:56:54
Источники:
Https://math-ege. sdamgia. ru/test? theme=294












































.png)

.png)