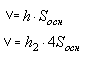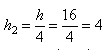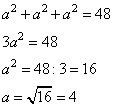Задания
Версия для печати и копирования в MS Word
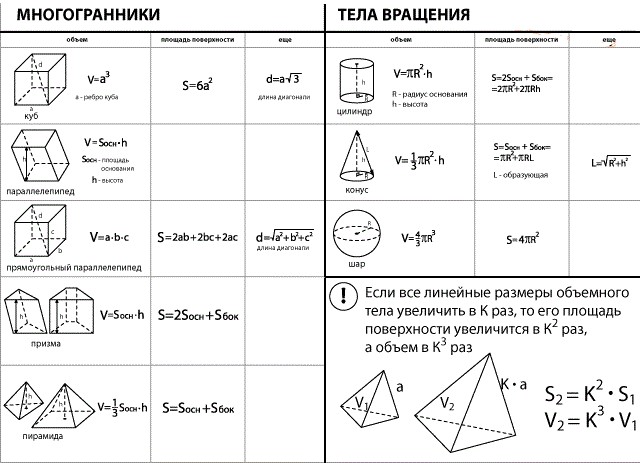
Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол в 60° и равно 2. Найдите объем параллелепипеда.
Спрятать решение
Решение.
Объем параллелепипеда вычисляется по формуле
Примем ромб за основание, тогда проведенная к нему высота
где L — длина бокового ребра, α — угол между боковым ребром и основанием (см. рис.). Площадь ромба равна квадрату его стороны, умноженной на синус угла ромба. Вычислим объем:
Ответ: 1,5.
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-23

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!
Профильный уровень переход на базовый уровень
РЕШЕНИЯ ЕГЭ ПО МАТЕМАТИКЕ — 2013
на нашем сайте
Копирование решений на другие сайты запрещено.
Вы можете поставить ссылку на эту страницу.
Наша система тестирования и подготовки к экзамену РЕШУ ЕГЭ РФ.
Наши справочные материалы для подготовки к экзамену.
Внимание! Мы не стремились привести самые короткие или самые красивые решения: каждый имеет право решать задачу так, как ему проще: одним удобнее за несколько минут заполнить страницу выкладками, другие предпочитают подумать, но получить короткое решение. Для аналогичных задач мы старались различные решения. Среди 2400 приведенных решений есть, конечно, и решения с опечатками. Заметите — сообщайте. Удачи!
C 2001 по 2009 год в России начался эксперимент по объединению выпускных экзаменов из школ со вступительными экзаменами в высшие учебные заведения. В 2009 году этот эксперимент был закончен, и с тех пор единый государственный экзамен стал основной формой контроля школьной подготовки.
В 2010 году на смену старой команде составителей экзамена пришла новая. Вместе с разработчиками изменилась и структура экзамена: уменьшилось число задач, увеличилось количество геометрических задач, появилась задача олимпиадного типа.
Важным нововведением стала подготовка открытого банка экзаменационных заданий, в котором разработчики разместили около 75 тысяч заданий. Решить эту бездну задач никто не в силах, но это и не нужно. В действительности, основные типы заданий, представлены так называемыми прототипами, их примеро 2400 штук. Все остальные задачи получены из них при помощи компьютерного клонирования; они отличаются от прототипов только конкретными числовыми данными.
Продолжая наши традиции мы представляем вашему вниманию решения всех прототипов экзаменационных заданий, существующих в открытом банке. После каждого прототипа приводится список составленных на его основе задач-клонов для самостоятельных упражнений.
Всё варианты 13 задания математика ЕГЭ Профиль 2020admin2020-08-06T14:25:33+03:00
Скачать задания в формате pdf.
Комментарии для сайта Cackle
Стереометрия
Задание №8 в профильном уровне ЕГЭ по математике проверяет базовые знания стереометрии. Задания в этом разделе простые, на базовые формулы – обычно на объемы простых стандартных фигур – цилиндра, куба, пирамиды, конуса.
Теория к заданию №8
Приведу формулы объема фигур, так данный материал довольно часто встречается.
Разбор типовых вариантов заданий №8 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого? Ответ выразите в см.
Алгоритм решения:
- Определяем площадь основания первого и второго сосудов.
- Записываем формулы объемов и приравниваем их.
- Убираем одинаковые величины. Делаем вывод.
- Записываем ответ.
Решение:
1. Площадь основания первого сосуда определяется формулой
Диаметр второго сосуда в 2 раза больше. Значит площадь основания его равна
то есть в 4 раза больше:
2 Записываем формулы объема жидкости в каждом сосуде.
Так как объем жидкости остается постоянным, получаем уравнение:
Убираем одинаковые величины. Отсюда
Ответ: 4.
Второй вариант задания (из Ященко, №1)
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 28. Найдите объём цилиндра.
Алгоритм решения:
- Записываем формулу объема конуса.
- Записываем формулу объема цилиндра.
- Сравниваем формулы, делаем вывод.
- Вычисляем объем цилиндра.
- Записываем ответ.
Решение:
1. Объем конуса определяем по формуле
где H – высота конуса; R – радиус основания конуса.
2. Объем цилиндра определяем по формуле
3. Сравниваем обе формулы. Легко видно, что объем цилиндра в 3 раза больше объема конуса.
4. Вычисляем объем цилиндра::
Ответ: 84.
Третий вариант задания (из Ященко)
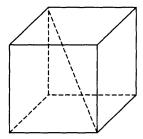
Диагональ куба равна . Найдите его объём.
Алгоритм решения:
- Выражаем диагональ куба, используя теорему Пифагора.
- Решаем полученное уравнение.
- Вычисляем объем.
- Записываем ответ.
Решение:
1. По тереме Пифагора диагональ грани куба определяется формулой:
Тогда диагональ куба
2. Отсюда
3. Объем куба равен
Ответ: 64.
Даниил Романович | Просмотров: 27.1k | Оценить:
Задание 2. Информатика. Апробация 10.03.2023
Миша заполнял таблицу истинности логической функции (F)
$$
(x to neg (y to z)) lor w,
$$
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных (w), (x), (y), (z).
| F | ||||
| 0 | 0 | 0 | ||
| 1 | 0 | |||
| 0 | 1 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных (w), (x), (y), (z).
В ответе напишите буквы (w), (x), (y), (z) в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Функция (F) задана выражением ( neg x lor y), зависящим от двух переменных, а фрагмент таблицы имеет следующий вид:
В этом случае первому столбцу соответствует переменная (y), а второму — переменная (x). В ответе следует написать: (yx).
Решение:
Python
from itertools import permutations, product
def F(x, y, z, w):
return (x <= (not y <= z)) or w
for perm in permutations('xyzw'):
for a,b,c,d,e,f,g in product([0,1], repeat=7):
table = [[a,0,b,0,0],
[1,c,d,e,0],
[0,1,f,g,0]]
if table[0] == table[1]:
continue
if all(F(**dict(zip(perm,row))) == row[-1] for row in table):
print(*perm)
Ответ: (yzxw)