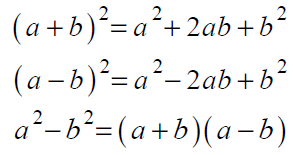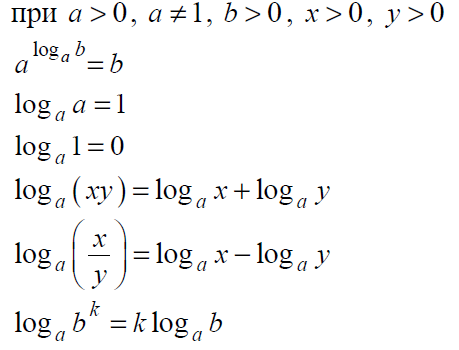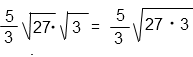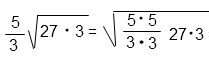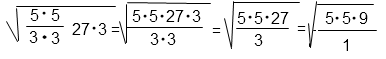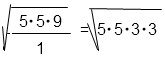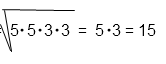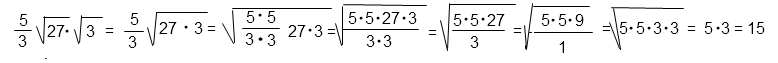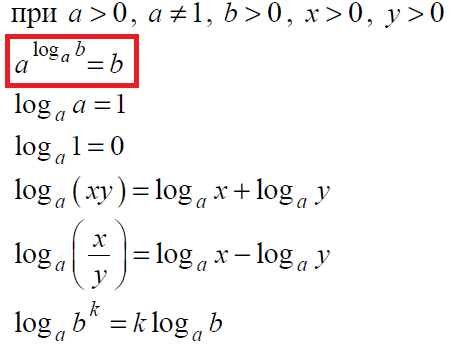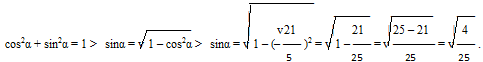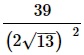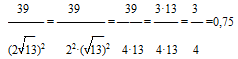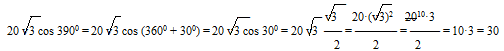Егэ математика 41054171 - Помощь в подготовке к экзаменам и поступлению

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Версия для печати и копирования в MS Word

Найдите корень уравнения

Ответ:

Проводится жеребьёвка Лиги Чемпионов. На первом этапе жеребьёвки восемь команд, среди которых команда «Барселона», распределились случайным образом по восьми игровым группам  — по одной команде в группу. Затем по этим же группам случайным образом распределяются еще восемь команд, среди которых команда «Зенит». Найдите вероятность того, что команды «Барселона» и «Зенит» окажутся в одной игровой группе.

Ответ:

Найдите если

Ответ:

В правильной треугольной пирамиде боковое ребро равно 5, а тангенс угла между боковой гранью и плоскостью основания равен Найти сторону основания пирамиды.

Ответ:

Функция y  =  f (x) определена и непрерывна на отрезке [−5; 5]. На рисунке изображён график её производной. Найдите точку x₀, в которой функция принимает наименьшее значение, если f (−5) ≥ f (5).

Ответ:

Весной катер идёт против течения реки в раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

Ответ:

Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая  — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая  — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Ответ:

Найдите наименьшее значение функции

Ответ:

а)  Решите уравнение $1 плюс ctg 2x= дробь: числитель: 1, знаменатель: косинус левая круглая скобка dfrac3 Пи 2 минус 2x правая круглая скобка конец дроби .$

б)  Укажите корни этого уравнения, принадлежащие промежутку

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

В кубе ABCDA₁B₁C₁D₁ все рёбра равны 4. На его ребре BB₁ отмечена точка K так, что KB = 3. Через точки K и C₁ построена плоскость α, параллельная прямой BD₁.

а)  Докажите, что A₁P : PB₁ = 2 : 1, где P  — точка пересечения плоскости α с ребром A₁B₁.

б)  Найдите угол наклона плоскости α к плоскости грани BB₁C₁C.

Решите неравенство

15-го декабря планируется взять кредит в банке на 1 000 000 рублей на (n + 1) месяц. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;

— cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца с 1-го по n-й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца;

— 15-го числа n-го месяца долг составит 200 тысяч рублей;

— к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен.

Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1378 тысяч рублей.

Высоты BB₁ и CC₁ остроугольного треугольника ABC пересекаются в точке H.

а)  Докажите, что ∠AHB₁ = ∠ACB.

б)  Найдите BC, если AH  =  4 и ∠BAC  =  60°.

Найдите все значения a, при которых уравнение

имеет ровно два решения.

Известно, что a, b, c, и d  — попарно различные положительные двузначные числа.

а)  Может ли выполняться равенство

б)  Может ли дробь быть в 11 раз меньше, чем сумма

в)  Какое наименьшее значение может принимать дробь если и

Завершить тестирование, свериться с ответами, увидеть решения.

Источник

Новый тренировочный вариант №41054171 ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.

Скачать вариант, скачать ответы

Решу ЕГЭ 2022 по математике профильный уровень тренировочный вариант №41054171

Ответы и решения для варианта:

Задание 2 № 500037 Проводится жеребьёвка Лиги Чемпионов. На первом этапе жеребьёвки восемь команд, среди которых команда «Барселона», распределились случайным образом по восьми игровым группам— по одной команде в группу. Затем по этим же группам случайным образом распределяются еще восемь команд, среди которых команда «Зенит». Найдите вероятность того, что команды «Барселона» и «Зенит» окажутся в одной игровой группе.

Ответ: 0,125

Задание 10 № 319353 Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая— 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая— 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Ответ: 0,019

Задание 13 № 509502 В кубе ABCDA1B1C1D1 все рёбра равны 4. На его ребре BB1 отмечена точка K так, что KB = 3. Через точкиK и C1 построена плоскость α, параллельная прямой BD1 . а) Докажите, что A1P : PB1 = 2 : 1, где P — точка пересечения плоскости α с ребром A1B1 . б) Найдите угол наклона плоскости α к плоскости грани BB1C1C.

Задание 15 № 520787 15-го декабря планируется взять кредит в банке на 1 000 000 рублей на ( n + 1) месяц. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца; — cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца с 1-го по n- й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца; — 15-го числа n-го месяца долг составит 200 тысяч рублей; — к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен. Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1378 тысяч рублей.

Ответ: 3

Задание 16 № 505425 Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H. а) Докажите, что ∠ AHB1 = ∠ACB. б) Найдите BC, если AH = 4 и ∠BAC = 60°.

Другие тренировочные варианты ЕГЭ по математике 11 класс:

28.09.2021 Математика 11 класс МА2110101-МА2110112 ЕГЭ 2022 работа статград ответы и задания

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Скачать вариант, скачать ответы

Решу ЕГЭ 2022 по математике профильный уровень тренировочный вариант №41054171

Ответы и решения для варианта:

Ответ: 0,125

Ответ: 0,019

Ответ: 3

Другие тренировочные варианты ЕГЭ по математике 11 класс:

28.09.2021 Математика 11 класс МА2110101-МА2110112 ЕГЭ 2022 работа статград ответы и задания

РЕШЕНИЯ ЕГЭ ПО МАТЕМАТИКЕ — 2013
на нашем сайте
Копирование решений на другие сайты запрещено.
Вы можете поставить ссылку на эту страницу.

Наша система тестирования и подготовки к экзамену РЕШУ ЕГЭ РФ.

Наши справочные материалы для подготовки к экзамену.

Внимание! Мы не стремились привести самые короткие или самые красивые решения: каждый имеет право решать задачу так, как ему проще: одним удобнее за несколько минут заполнить страницу выкладками, другие предпочитают подумать, но получить короткое решение. Для аналогичных задач мы старались различные решения. Среди 2400 приведенных решений есть, конечно, и решения с опечатками. Заметите — сообщайте. Удачи!

C 2001 по 2009 год в России начался эксперимент по объединению выпускных экзаменов из школ со вступительными экзаменами в высшие учебные заведения. В 2009 году этот эксперимент был закончен, и с тех пор единый государственный экзамен стал основной формой контроля школьной подготовки.

В 2010 году на смену старой команде составителей экзамена пришла новая. Вместе с разработчиками изменилась и структура экзамена: уменьшилось число задач, увеличилось количество геометрических задач, появилась задача олимпиадного типа.

Важным нововведением стала подготовка открытого банка экзаменационных заданий, в котором разработчики разместили около 75 тысяч заданий. Решить эту бездну задач никто не в силах, но это и не нужно. В действительности, основные типы заданий, представлены так называемыми прототипами, их примеро 2400 штук. Все остальные задачи получены из них при помощи компьютерного клонирования; они отличаются от прототипов только конкретными числовыми данными.

Продолжая наши традиции мы представляем вашему вниманию решения всех прототипов экзаменационных заданий, существующих в открытом банке. После каждого прототипа приводится список составленных на его основе задач-клонов для самостоятельных упражнений.

Значение выражений

Описание задания

В задании №5 ЕГЭ по математике базового уровня нам необходимо вычислить значение выражения, пользуясь различными правилами: формулами сокращенного умножения, знаниями тригонометрии, свойствами логарифмов и другими. Данное задание требует более глубоких знаний и значительно сложнее первого задания, где достаточно было знать элементарные математические операции.

Тематика заданий: значение выражений

Бал: 1 из 20

Сложность задания: ♦♦♦

Примерное время выполнения: 5-7 мин.

Теория к заданию №5

В данном задании, кроме операций со степенями, о которых мы говорили в прошлых заданиях, необходимо помнить формулы сокращенного умножения:

Кроме этого, очень часто встречаются задания на знания свойств логарифма:

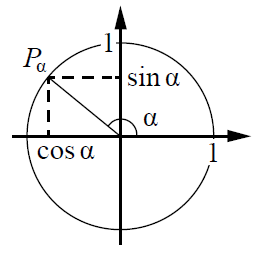
Полезными будут представления о тригонометрической окружности, по которой можно определять знаки тригонометрических функций:

Разбор типовых вариантов заданий №5 ЕГЭ по математике базового уровня

Во всех заданиях необходимо найти значение выражения.

Вариант 5МБ1

Алгоритм выполнения

Представим угол 390° с учетом периодичности функции tg меньшим углом.
Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.
Выполним умножение.

Решение:

Функция tg является периодической с периодом 180°, то есть каждый раз при увеличении или уменьшении угла на 180° значение tg повторяется.

То есть tg α = tg (α + 180°) = tg (α – 180°)

tg 390° = tg (390° – 180°) = tg 210° = tg (210° – 180°) = tg 30°

Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.

tg 30° = √3/3

Подставим найденное значение в данное выражение.

20 · √3 · (√3/3) = (20 · √3 · √3)/3 = (20 · 3)/3 = 20

Решение в общем виде

Вычислим выражение, учитывая, что функция тангенс периодическая с периодом π радиан или 180°. Следовательно, угол 390° эквивалентен углу

и получаем выражение:

Ответ: 20.

Вариант 5МБ2

Алгоритм выполнения

Представим угол 420° с учетом периодичности функции tg меньшим углом.
Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.
Выполним умножение.

Решение №1:

То есть

tg α = tg (α + 180°) = tg (α – 180°)

tg 390° = tg (420° – 180°) = tg 240° tg (240° – 180°) = tg 60°

Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.

tg 60° = √3

Подставим найденное значение в данное выражение.

-50 · √3 · √3 = -50 · 3 = -150

Решение №2:

Заметим, что функция тангенс периодическая с периодом π радиан или 180°. Поэтому, тангенс угла 420° эквивалентен тангенсу угла в

получаем:

Ответ: -150.

Вариант 5МБ3

Алгоритм выполнения

Объединим подкоренные выражения под один корень.
Внесем под корень дробь.
Сократим дробь под корнем.
Представим произведение под корнем в виде произведения вторых степеней.
Вынесем из под корня множители.
Выполним умножение.

Решение:

Объединим подкоренные выражения под один корень. Имеем право так сделать использовав, свойство квадратного корня.

5/3 · √27 · √3 = 5/3 · √(27 · 3)

Внесем под корень дробь.

Корень квадратный, следовательно, чтобы внести дробь под знак корня нужно возвести ее в квадрат. То есть умножить сам на себя числитель и знаменатель.

(5/3)² = (5 · 5)/(3 · 3)

Сократим дробь под корнем на три дважды.

Представим произведение под корнем в виде произведения вторых степеней.

Вынесем из под корня множители и выполним умножение.

Решение в общем виде:

Ответ: 15.

Вариант 5МБ4

Найдите cos α, если sin α = 0,8 и 90° ‹ α ‹ 180°.

Алгоритм выполнения

Запишем основное тригонометрическое тождество.
Подставим в основное тригонометрическое тождество все известные данные.
Решим полученное уравнение относительно cos α.
Выбрать корни, подходящие к условию задания.

Решение:

Запишем основное тригонометрическое тождество.

sin² α + cos² α = 1

Подставим в основное тригонометрическое тождество все известные данные.

0,8² + cos² α = 1

Решим полученное уравнение относительно cos α.

cos² α – неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.

cos² α = 1 – 0,8²

Чтобы найти вторую степень числа нужно число умножить само на себя.

0,8² = 0,8 · 0,8 = 0,64

cos² α = 1 – 0,8² 1 – 0,64 = 0,36

cos α = √0,36

cos α = 0,6 или -0,6

Условие 90° ‹ α ‹ 180° означает, что -1 ‹ соs α ‹ 0.

Следовательно данному условию удовлетворяет только один корень -0,6.

Ответ: -0,6.

Вариант 5МБ5

Алгоритм выполнения

В данном задании необходимо сразу заметить формулу сокращенного умножения – разность квадратов (последняя формула сокращенного умножения в теории выше).

Решение:

После этого, решение задания сводится к следующему:

(2√13 −1)(2√13 +1) = (2√13)² – 1² = 4 • 13 – 1 = 51

Ответ: 51.

Вариант 5МБ6

Алгоритм выполнения

Сначала вспомним свойства степеней и разложим выражение следующим образом:

5^log₅6 • 5¹

Затем вспомним определение и свойство логарифма – это вторая строчка из нашей теории:

Решение:

Получим:

6•5 = 30

Ответ: 30

Вариант 5МБ7

Алгоритм выполнения

Применяем формулу сокращенного умножения a²–b²=(a-b)(a+b).
Используем определение кв.корня: (√a)²=a.
Находим полученную разность целых чисел.

Решение:

Исходя из алгоритма, подставляем а=√11, а b=√3, тогда 11-3=8

Ответ: 8

Вариант 5МБ8

Алгоритм выполнения

Применяем тождество log_a(xy)=log_ax+log_ay.
Преобразовываем множители, стоящие под знаком логарифма, в степени.
Используем для выражения под знаком логарифма св-во степеней a^xb^x=(ab)^x.
Используем св-во логарифмов xlog_ab=log_ab^x.
Применяем тождество log_aa=1,.

Решение:

log₆27 + log₆8 = log₆27·8 = log₆3³·2³ = log₆(3·2)³ = log₆6³ = 3log₆6 = 3

Ответ:3

Вариант 5МБ9

Алгоритм выполнения

Вносим множитель √6 в скобки.
Выполняем умножение √24 и √6. Получим √144. Это число является полным квадратом: (√12)².
Перемножаем √6 и √6. Получаем (√6)².
Используя определение кв.корня (√а)²=а, находим, что (√12)²=12, а (√6)²=6.
Находим разность полученных целых чисел.

Решение:

Ответ: 6

Вариант 5МБ10

Найдите sinα, если

Алгоритм выполнения

Применим основное тригонометрическое тождество. В тождество подставим данное в условии числовое значение для косинуса.
Выполняем преобразование тождества, получаем числовой результат.
Определяем знак результата, исходя из величины угла α.

Решение:

Ответ: 0,4

Вариант 5МБ11

Алгоритм выполнения

Выполняем 1-ю по приоритетности операцию – возведение в степень (в знаменателе). Для этого используем св-во степеней (ab)²=a²·b². Далее для множителя (√13)² применяем формулу, определяющую понятие кв.корня: (√а)²=а.
Выполняем умножение в знаменателе.
Представляем число 39 в числителе как произведение 3·13.
Сокращаем дробь на 13.
Переводим полученную обыкновенную дробь в десятичную.

Решение:

Ответ: 0,75

Вариант 5МБ12

Алгоритм выполнения

Применяем к показателю степени 2log₃7 св-во логарифмов log_b^ya^x=(x/y)log_ba. Получим log₃7².
Применяем св-во логарифмов a^log_a^b=b. В результате знак логарифма исчезает, остается только выражение 7², которое было под знаком логарифма.
Возводим 7 в квадрат.

Решение:

2log₃7 log₃7²

3 = 3 = 7² = 49

Ответ:49

Вариант 5МБ13

Алгоритм выполнения

Используем св-во корней √(a·b)=√a·√b. Таким способом √63 разложим на множители √9 и √7.
Сгруппируем одинаковые множители √7. Получим (√7)².
Основываясь на определении кв.корня (√а)²=а, представляем √9=(√3)².
Возводим полученные числа в квадрат.
Находим итоговое произведение.

Решение:

Ответ: 21

Вариант 5МБ14

Алгоритм выполнения

Используем св-во степеней x^a+b=x^a·x^b. Получим 2 множителя, первый из которых равен 7, а второй представляет собой степень с основанием 7 и показателем, содержащим логарифм.
Для второго множителя применим св-во логарифмов a^loga^b=b.
Находим результирующее произведение.

Решение:

Ответ: 21

Вариант 5МБ15

Алгоритм выполнения

Для cos 390⁰ используем ф-лу приведения cos (360⁰+α)=cos α. Получим cos 30⁰=√3/2. Записываем получившееся выражение в виде дроби со знаменателем 2.
Вычисляем произведение √3·√3 путем возведения в степень. Для этого используем определение кв.корня: (√а)²=а.
Сокращаем 20 в числителе и 2 в знаменателе на 2.
Находим конечное произведение.

Решение:

Ответ: 30

Вариант 5МБ16

Алгоритм выполнения

Преобразовываем часть выражения, взятую в скобки. Для этого представляем 49 как 7². Затем используем св-во логарифмов log_ba^x=xlog_ba, а далее св-во log_aa=1. Получаем 2.
Применяем св-во логарифмов log_aa=1.

Решение:

log₂(log₇49) = log₂(log₇7²) = log₂(2log₇7) = log₂2 = 1

Ответ: 1

Источник

Перейти к содержанию

На чтение 1 мин Просмотров 1 Опубликовано 5 марта, 2023

Решу ЕГЭ 2022 тренировочный вариант №41054171 по математике профильный уровень 11 класс с ответами Решение и ответы на задачи на официальном сайте источника онлайн.

Новый тренировочный вариант №41054171 ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии

Варианты ответов и решение задачи ТУТ: https://100ballnik.com/%d1%80%d0%b5%d1%88%d1%83-%d0%b5%d0%b3%d1%8d-2022-%d1%82%d1%80%d0%b5%d0%bd%d0%b8%d1%80%d0%be%d0%b2%d0%be%d1%87%d0%bd%d1%8b%d0%b9-%d0%b2%d0%b0%d1%80%d0%b8%d0%b0%d0%bd%d1%82-%e2%84%9641054171-%d0%bf/

Ответы и решение задачи онлайн

Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.

Источник

Егэ по математике 2022 решуегэ

Решу ЕГЭ 2022 по математике профильный уровень тренировочный вариант №41054171

Ответы и решения для варианта:

Ответ: 0,125

Ответ: 0,019

Задание 15 № 520787 15-го декабря планируется взять кредит в банке на 1 000 000 рублей на ( n + 1) месяц. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца; — cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца с 1-го по n — й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца; — 15-го числа n-го месяца долг составит 200 тысяч рублей; — к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен. Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1378 тысяч рублей.

Ответ: 3

Решу ЕГЭ 2022 тренировочный вариант №41054171 по математике профильный уровень 11 класс с ответами

Ответ: 0,125

Ответ: 0,019

Задание 15 № 520787 15-го декабря планируется взять кредит в банке на 1 000 000 рублей на ( n + 1) месяц. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца; — cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца с 1-го по n — й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца; — 15-го числа n-го месяца долг составит 200 тысяч рублей; — к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен. Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1378 тысяч рублей.

Ответ: 3

Затем по этим же группам случайным образом распределяются еще восемь команд, среди которых команда Зенит.

100ballnik. com

19.10.2020 21:11:39

2020-10-19 21:11:39

Источники:

Https://100ballnik. com/%D1%80%D0%B5%D1%88%D1%83-%D0%B5%D0%B3%D1%8D-2022-%D1%82%D1%80%D0%B5%D0%BD%D0%B8%D1%80%D0%BE%D0%B2%D0%BE%D1%87%D0%BD%D1%8B%D0%B9-%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82-%E2%84%9641054171-%D0%BF/

Решу ЕГЭ математика профиль 2022 » /> » /> .keyword { color: red; } Егэ по математике 2022 решуегэ

Решу ЕГЭ математика профиль 2022 — базовый и профильный уровни экзамена

Решу ЕГЭ математика профиль 2022 поможет подготовиться к единому государственному экзамену по математике, который поводится в качестве обязательного для всех выпускников средних учебных заведений, то есть школ, лицеев и гимназий.

Математика

Что представляет собой ЕГЭ математика? Данный экзамен разделён на два уровня: базовый и профильный. Первый предназначен для тех выпускников, которые не планируют продолжать обучение в вузах вовсе, а также для тех, кто поступает в вузы, где в качестве вступительных испытаний отсутствует предмет «Математика».

Профильный уровень предназначен для выпускников, планирующих продолжать обучение в высших учебных заведениях, при поступлении в которые необходимо сдавать математику.

Отыскать тренировочные варианты как базового, так и профильного уровней можно на ресурсе Решу ЕГЭ. Обновление таких вариантов происходит каждый месяц. При этом варианты составляются из новых заданий, а также тех заданий, которые оказались наиболее сложными по результатам предшествующего месяца. При желании можно обратиться не только к вариантам текущего, но и прошлых месяцев. Сделать это можно по ссылке «Прошлые месяцы». В результате откроется архив вариантов, где среди прочих представлен и 2022 год.

Решу ЕГЭ

После того как работа оказывается выполненной, система осуществляет проверку представленных ответов, показывает правильные решения, а также выставляет оценку.

Помимо тренировочных доступным является персональный вариант. Его формирование осуществляется искусственным интеллектом. Включает такой вариант 10 заданий, которые зависят от накопленной статистики. При этом учитывается текущий уровень, ранее решённые, нерешённые, а также вызвавшие затруднение задания. Для возможности выполнять задания персонального варианта требуется авторизоваться на портале Решу ЕГЭ, то есть осуществить вход в профиль. Перед этим в свою очередь необходимо выполнить регистрацию.

Для регистрации следует перейти по одноимённой ссылке, представленной в правой части веб-страницы Решу ЕГЭ. После этого будет предложено ввести свои данные. Это адрес электронной почты, который в дальнейшем будет использоваться в качестве логина. Также необходимо указать имя и фамилию. Далее следует дважды ввести пароль. Необходимо указать и дату рождения.

Регистрация

Зарегистрироваться на сайте может ученик, учитель и родитель. Пользователю необходимо выбрать подходящую ему роль. После регистрации родитель может сообщить своему ребёнку логин и попросить предоставить доступ к статистике. Это позволит получать уведомления, касающиеся домашних заданий и выставленных отметок. В том случае если дать разрешение на получение уведомлений с сайта в настройках браузера, то возможным станет получение уведомлений на своё устройство без необходимости заходить на сайт.

После того как все необходимые для регистрации данные указаны, нужно принять правила пользования сайтом и дать согласие на обработку персональных данных. Далее следует нажать на кнопку «Зарегистрироваться». В результате появится профиль на веб-ресурсе Решу ЕГЭ, вход в который можно осуществить в любое удобное для себя время.

Для того чтобы выполнить вход, потребуется указать электронную почту и пароль в специально предназначенных для этого полях в левой части сайта. После этого останется нажать на кнопку «Войти». В случае необходимости можно восстановить пароль. Для этого потребуется воспользоваться соответствующей ссылкой, после чего сообщить адрес электронной почты, который был указан в ходе регистрации, и нажать на «Отправить». После восстановления пароля можно будет осуществить вход в профиль. Выполнить вход можно и через социальную сеть ВКонтакте.

Вход в профиль

Помимо тренировочных и персонального вариантов доступным является и вариант учителя. Для того чтобы обратиться к нему, необходимо знать его номер. Такой номер следует указать в специально предназначенное для этого поле, после чего нажать на кнопку «Открыть».

Помимо прочего сайт Решу ЕГЭ позволяет осуществлять поиск в каталоге. Здесь можно искать задания демоверсий, банков пробных работ, прошедших экзаменов с решениями. Для поиска необходимо знать номер или текст задания, которые потребуется ввести в специально предназначенное для этого поле, а затем нажать на кнопку «Открыть».

Ещё одна возможность — конструктор варианта по типам и по темам, позволяющий целенаправленно тренироваться по конкретным темам. Конструктор позволяет составить вариант из нужного количества заданий, представленных в тех или иных разделах задачного каталога.

Что представляет собой базовый уровень математика 2022? Это 21 задание тестовой части, касающиеся вычислений, простейших текстовых задач, размеров и единиц измерений, чтения графиков и диаграмм, задач на квадратной решётке. Для успешной сдачи базового уровня экзамена также понадобятся знания и умения, связанные с вычислениями и преобразованиями, преобразованием выражений, простейших уравнений прикладной геометрии, начал теории вероятностей.

Базовый уровень

Среди тем представлены и выбор оптимального варианта, стереометрия, анализ графиков и диаграмм, планиметрия, неравенства, анализ утверждений, числа и свойства. Также предлагаются текстовые задачи и задачи на смекалку.

Что представляет собой ЕГЭ математика профильного уровня в 2022 году? Это 11 заданий тестовой части и 7 заданий развёрнутой. Какие именно темы охватывают задания, которые потребуется выполнить во время сдачи единого государственного экзамена?

Задания тестовой части касаются простейших уравнений, начал теории вероятностей, планиметрии, вычислений и преобразований, стереометрии, производной и первообразной, задач с прикладным содержанием, текстовых задач, графиков функций, вероятностей сложных событий, наибольшего и наименьшего значения функций.

Профильный уровень

Развёрнутая часть профильного уровня ЕГЭ математика 2022 включает уравнения, стереомерическую задачу, неравенства, финансовую математику, планиметрическую задачу, задачу с параметром, задание на числа и их свойства.

Для того чтобы подготовиться к экзамену и успешно его сдать, среди прочего сайт Решу ЕГЭ предлагает выполнять задания, представленные в вариантах Александра Ларина. Такие задания подойдут для тех, кто ищет более сложные варианты, чем обычно предлагают на ЕГЭ. На веб-ресурсе можно отыскать задания с развёрнутым ответом. Новые условия размещаются по субботам, а решения появляются по пятницам.

Таким образом, сайт Решу ЕГЭ позволяет подготовиться к экзамену по математике, выполняя задания различных вариантов. Здесь представлены как задания для тех, кто планирует сдавать базовый уровень данного предмета, так и для тех, кому необходимо сдавать профильный уровень математики для поступления в вузы.

Математика

Решу ЕГЭ

Первый предназначен для тех выпускников, которые не планируют продолжать обучение в вузах вовсе, а также для тех, кто поступает в вузы, где в качестве вступительных испытаний отсутствует предмет Математика.

Reshu-ege. su

24.10.2019 4:37:32

2019-10-24 04:37:32

Источники:

Https://reshu-ege. su/matematika-profil-2022/

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Егэ по математике 2022 решуегэ

Егэ по математике 2022 решуегэ

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

—>

Тела вращения.

Для прохождения вариантов, созданных учителем, войдите на сайт.

Наверх

—>

Выставленные учителем баллы отобразятся в вашей статистике.

Ege. sdamgia. ru

18.11.2020 20:09:08

2020-11-18 20:09:08

Источники:

Https://ege. sdamgia. ru/test? id=45483359

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.

ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.admin2023-03-05T19:16:30+03:00

Источник

Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.

Варианты составлены в соответствии с демоверсией 2023 года

Тренировочные варианты ЕГЭ 2023 по математике (профиль)

vk.com/pezhirovschool
Вариант 1	решения
Вариант 2	решения
Вариант 3	решения
Вариант 4	решения
Вариант 5 (с ответами)
Вариант 6 (с ответами)
Вариант 7 (с ответами)
Вариант 8 (с ответами)
egemath.ru
вариант 1	скачать
вариант 2	скачать
вариант 3	скачать
вариант 4	скачать
вариант 5	скачать
вариант 6	скачать
вариант 7	скачать
вариант 8	скачать
вариант 9	скачать
вариант 10	скачать
вариант 11	скачать
вариант 12	скачать
вариант 13	скачать
вариант 14	скачать
вариант 15	скачать
вариант 16	скачать
вариант 17	скачать
вариант 18	скачать
вариант 19	скачать
вариант 20	скачать
time4math.ru
вариант 1-2	ответы
вариант 3-4	ответы
вариант 5-6	ответы
вариант 7-8
yagubov.ru
вариант 33 (сентябрь)	ege2023-yagubov-prof-var33
вариант 34 (октябрь)	ege2023-yagubov-prof-var34
вариант 35 (ноябрь)	ege2023-yagubov-prof-var35
вариант 36 (декабрь)	ege2023-yagubov-prof-var36
вариант 37 (январь)	ege2023-yagubov-prof-var37
вариант 38 (февраль)	ege2023-yagubov-prof-var38
math100.ru (с ответами)
variant 179	скачать
variant 180	скачать
variant 181	скачать
variant 182	скачать
variant 183	скачать
variant 184	скачать
variant 185	скачать
variant 186	скачать
variant 187	скачать
variant 188	скачать
variant 189	скачать
variant 190	скачать
variant 191	скачать
variant 192	скачать
variant 193	скачать
variant 194	скачать
variant 195	скачать
variant 196	скачать
variant 197	скачать
variant 198	скачать
variant 199	скачать
variant 200	скачать
variant 201	скачать
variant 202	скачать
variant 203	скачать
variant 204	скачать
variant 205	скачать
alexlarin.net
Вариант 397	проверить ответы
Вариант 398	проверить ответы
Вариант 399	проверить ответы
Вариант 400	проверить ответы
Вариант 401	проверить ответы
Вариант 402	проверить ответы
Вариант 403	проверить ответы
Вариант 404	проверить ответы
Вариант 405	проверить ответы
Вариант 406	проверить ответы
Вариант 407	проверить ответы
Вариант 408	проверить ответы
Вариант 409	проверить ответы
Вариант 410	проверить ответы
Вариант 411	проверить ответы
Вариант 412	проверить ответы
Вариант 413	проверить ответы
vk.com/ege100ballov
вариант 1	скачать
вариант 2	скачать
вариант 3	скачать
вариант 4	скачать
вариант 5	скачать
вариант 6	скачать
вариант 7	скачать
вариант 8	скачать
вариант 9	скачать
вариант 10	скачать
вариант 11	скачать
vk.com/math.studying
Вариант 1	ответы
vk.com/marsel_tutor
Вариант 1	разбор
Вариант 2	конспект / разбор
Вариант 3	конспект / разбор
Вариант 4	конспект / разбор
Вариант 5	конспект / разбор
Вариант 6	разбор
vk.com/shkolkovo_easy_math
Вариант 1	решение
Вариант 2	решение
Вариант 3	решение
Вариант 5	решение
Вариант 6	решение
vk.com/mathlearn_ru
вариант 1	разбор
vk.com/ekaterina_chekmareva
Вариант 1	ответы
Вариант 2	ответы
Вариант 3	ответы
Вариант 4	ответы
Вариант 5	ответы
Вариант 6	ответы
Вариант 7	ответы
Вариант 8	ответы

Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня

Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:

– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;

– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).

Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.

Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.

Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.

Примеры заданий:

1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.

2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу

3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).

а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.

б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?

в) Найдите наибольшее возможное значение суммы получившихся чисел.

Смотрите также:

Источник

Решу ЕГЭ 2022 по математике профильный уровень тренировочный вариант №41054171

Ответы и решения для варианта:

Другие тренировочные варианты ЕГЭ по математике 11 класс:

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

ПОДЕЛИТЬСЯ

Решу ЕГЭ 2022 по математике профильный уровень тренировочный вариант №41054171

Ответы и решения для варианта:

Другие тренировочные варианты ЕГЭ по математике 11 класс:

Значение выражений

Теория к заданию №5

Разбор типовых вариантов заданий №5 ЕГЭ по математике базового уровня

Вариант 5МБ1

Алгоритм выполнения

Решение:

Решение в общем виде

Вариант 5МБ2

Алгоритм выполнения

Решение №1:

Решение №2:

Вариант 5МБ3

Алгоритм выполнения

Решение:

Вариант 5МБ4

Алгоритм выполнения

Решение:

Вариант 5МБ5

Алгоритм выполнения

Решение:

Вариант 5МБ6

Алгоритм выполнения

Решение:

Вариант 5МБ7

Алгоритм выполнения

Решение:

Вариант 5МБ8

Алгоритм выполнения

Решение:

Вариант 5МБ9

Алгоритм выполнения

Решение:

Вариант 5МБ10

Алгоритм выполнения

Вариант 5МБ11

Алгоритм выполнения

Вариант 5МБ12

Алгоритм выполнения

Решение:

Вариант 5МБ13

Алгоритм выполнения

Вариант 5МБ14

Алгоритм выполнения

Решение:

Вариант 5МБ15

Алгоритм выполнения

Решение:

Вариант 5МБ16

Алгоритм выполнения

Решение:

Ответы и решение задачи онлайн

Решу ЕГЭ 2022 по математике профильный уровень тренировочный вариант №41054171

Ответы и решения для варианта:

Решу ЕГЭ 2022 тренировочный вариант №41054171 по математике профильный уровень 11 класс с ответами

Источники:

Решу ЕГЭ математика профиль 2022 — базовый и профильный уровни экзамена

Решу ЕГЭ математика профиль 2022 — базовый и профильный уровни экзамена

Источники:

Егэ по математике 2022 решуегэ

Егэ по математике 2022 решуегэ

Тела вращения.

Источники:

ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.

Новое и интересное на сайте: