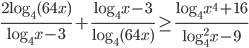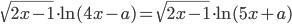15‐го декабря 2018 года Саша и Паша взяли в банке одинаковые суммы в кредит на 12 месяцев. Банк предложил им похожие схемы погашения долга. Условия возврата кредита у Саши оказались следующие:
‐ 1‐го числа каждого месяца долг возрастает на 10 % по сравнению с концом предыдущего месяца;
‐ со 2‐го по 14‐е число месяца необходимо выплачивать одним платежом часть долга.
‐ на 15‐е числа каждого месяца долг должен быть на одну и ту же сумму меньше долга, чем на 15‐е число предыдущего месяца.
У Паши условия возврата кредита были таковы:
‐ 1‐го числа каждого месяца долг возрастает на 10 % по сравнению с концом предыдущего месяца;
‐ со 2‐го по 14‐е число месяца необходимо выплачивать одним платежом часть долга. ‐ на 15‐е число каждого месяца с января по ноябрь включительно долг должен уменьшаться на 50 тыс. руб.
‐ в декабре 2019 года весь оставшийся на тот момент долг должен быть полностью погашен.
Когда в декабре 2019 года Саша и Паша рассчитались со своими кредитами, выяснилось, что один из них выплатил за год банку на 429 тыс. руб. больше, нежели другой. Определите, какая сумма была взята каждым в кредит.
Ответ: 1,38 млн. руб.
ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 301 (C часть).
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Цена на электрический чайник была повышена на 14% и составила 1596 рублей. Сколько рублей стоил чайник до повышения цены?
Ответ:
2
На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н · м. Скорость автомобиля (в км/ч) приближенно выражается формулой где n — число оборотов двигателя в минуту. С какой наименьшей скоростью должен двигаться автомобиль, чтобы крутящий момент был равен 120 Н · м? Ответ дайте в километрах в час.
Ответ:
3
На клетчатой бумаге с размером клетки
изображен треугольник АВС. Найдите длину его высоты, опущенной на сторону ВС.
Ответ:
4
Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Ответ:
5
Найдите корень уравнения
Ответ:
6
Четырехугольник ABCD вписан в окружность. Угол ABC равен 105°, угол CAD равен 35°. Найдите угол ABD. Ответ дайте в градусах.
Ответ:
7
8
Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
Ответ:
9
Найдите значение выражения
Ответ:
10
11
Расстояние между пристанями A и B равно 120 км. Из A в B по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в
Ответ:
12
Найдите точку максимума функции
Ответ:
13
а) Решите уравнение:
б) Определите, какие из его корней принадлежат отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
14
На рёбрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причём AM : BM = CN : NB = 1 : 2. Точки P и Q — середины ребер DA и DC соответственно.
а) Докажите, что P, Q, M и N лежат в одной плоскости.
б) Найти отношение объёмов многогранников, на которые плоскость PQM разбивает пирамиду.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
15
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
16
Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K, так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.
а) Докажите, что CO = KO.
б) Найти отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет площади трапеции ABCD.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
17
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
− каждый январь долг увеличивается на r% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплачивать одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рублей, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рублей, то кредит будет полностью погашен за 2 года. Найдите r.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
18
Найти все значения a, при каждом из которых уравнение
имеет ровно один корень на отрезке [0; 1].
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
19
На доске написано 30 различных натуральных чисел, десятичная запись каждого из которых оканчивается или на цифру 2, или на цифру 6. Сумма написанных чисел равна 2454.
а) Может ли на доске быть поровну чисел, оканчивающихся на 2 и на 6?
б) Может ли ровно одно число на доске оканчиваться на 6?
в) Какое наименьшее количество чисел, оканчивающихся на 6, может быть записано на доске?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
| 2093 | Найдите все значения a, при которых система уравнений { ((x^2+y^2-2x+2y-6)/sqrt(2-abs(y-x))=0) , (y-ax=3a-3) :} имеет ровно одно решение |
Найдите все значения a, при которых система уравнений {((x^2+y^2-2x+2y-6)/sqrt(2-abs(y-x))=0) , (y-ax=3a-3) :} ! ларин егэ по математике 2020 профильный уровень Вариант 301 Задание 18 # Решение от Елены Ильиничны Хажинской | |
| 2092 | В треугольнике ABC сторона ВC больше стороны АC. Биссектриса CL пересекает описанную около треугольника ABC окружность в точке К. Окружность, описанная около треугольника AKL вторично пересекает прямую АС в точке P. а) Докажите, что отрезки BC и PC равны. б) Найдите площадь треугольника APK, если BC=6, AB=5, АС=4 |
В треугольнике ABC сторона ВC больше стороны АC. Биссектриса CL пересекает описанную около треугольника ABC окружность в точке К ! ларин егэ по математике 2020 профильный уровень Вариант 301 Задание 16 # Решение от Елены Ильиничны Хажинской | |
| 2086 | Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен sqrt3, если известно, что высота призмы равна 6 |
Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен корень из 3 ! Тренировочный вариант 301 от Ларина Задание 8 | |
| 2085 | Найдите корень уравнения (2x-1.4)^3=-512 |
Найдите корень уравнения (2x-1,4)^3=-512 !Тренировочный вариант 301 от Ларина Задание 5 ЕГЭ | |
| 2084 | Имеется два сплава. Первый сплав содержит 5% меди, второй – 95% меди. Масса второго сплава меньше массы первого на 90 кг. Из этих двух сплавов получили третий сплав, содержащий 45% меди. Найдите массу третьего сплава. Ответ дайте в килограммах |
Имеется два сплава. Первый сплав содержит 5% меди, второй – 95% меди ! Тренировочный вариант 301 от Ларина Задание 11 | |
| 2083 | Найдите точку максимума функции y=(6-4x)cos(x)+4sin(x)+4, принадлежащую промежутку (-pi/2; pi). |
Тренировочный вариант 301 от Ларина Задание 12 | |
| 2082 | а) Решите уравнение sin(2x)+sqrt(3)(cos(x)-sin(x))=1.5 б) Укажите корни этого уравнения, принадлежащие промежутку [-(7pi)/2; -2pi]. |
Тренировочный вариант 301 от Ларина Задание 13 ЕГЭ # Решения: 1) от Кирилла Колокольцева (Москва) 2) Наталья Юрьевна — (Пользователь netka, Казань) | |
| 2081 | Решите неравенство x^2/log_{(5-x)}(x)<=(5x-4)*log_{x}(5-x) |
Тренировочный вариант 301 от Ларина Задание 15 | |
Реальный вариант № 301
Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий с кратким ответом базового уровня сложности. Часть 2 содержит 4 задания с кратким ответом повышенного уровня сложности и 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–12 записываются по приведённому ниже образцу в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите их в бланк ответов № 1.
При выполнении заданий 13–19 требуется записать полное решение и ответ в бланке ответов № 2.
Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой, или капиллярной, или перьевой ручек.
При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы. Баллы, полученные Вами за выполненные задания, суммируются.
Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
Условия задач и ответы
Часть 1
Ответом к заданиям 1–12 является целое число или конечная десятичная дробь. Запишите число в поле ответа в тексте работы, затем перенесите его в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания, начиная с первой клеточки. Каждую цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно.
- Цена на электрический чайник была повышена на 25% и составила 1625 рублей. Сколько рублей стоил чайник до повышения цены?
- На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На горизонтальной оси отмечено число оборотов в минуту, на вертикальной оси — крутящий момент в Н ⋅ м. Определите по графику крутящий момент, если двигатель совершал 5000 оборотов в минуту. Ответ дайте в Н ⋅ м.
- На клетчатой бумаге с размером клетки 1 × 1 изображён треугольник ABC. Найдите длину его биссектрисы, проведённой из вершины B.
- www.itmathrepetitor.ru В среднем из 2000 садовых насосов, поступивших в продажу, 12 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
- Найдите корень уравнения
- Четырёхугольник ABCD вписан в окружность. Угол ABC равен 98°, угол CAD равен 44°. Найдите угол ABD. Ответ дайте в градусах.
- На рисунке изображён график функции
. На оси абсцисс отмечено восемь точек:
. В ответе укажите количество
точек (из отмеченных), в которых производная функцииположительна.
- Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности конуса равна
. Найдите площадь боковой поверхности цилиндра.
Часть 2
- Найдите значение выражения
- www.itmathrepetitor.ru Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с фокусным расстоянием f = 36 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 30 см до 50 см, а расстояние d2 от линзы до экрана — в пределах от 160 см до 180 см. Изображение на экране будет чётким, если выполнено соотношение
.
На каком наименьшем расстоянии от линзы нужно поместить лампочку, чтобы её изображение на экране было чётким? Ответ дайте в сантиметрах. - Теплоход, скорость которого в неподвижной воде равна 27 км/ч, проходит некоторое расстояние по реке и после стоянки возвращается в исходный пункт. Скорость течения равна 1 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 32 часа после отправления из него. Сколько километров проходит теплоход за весь рейс?
- Найдите точку минимума функции
- а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку.
- На рёбрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причём AM : MB = CN : NB = 1 : 2. Точки P и Q — середины рёбер DA и DC соответственно.
а) Докажите, что точки P, Q, M и N лежат в одной плоскости.
б) Найдите отношение объёмов многогранников, на которые плоскость PQM разбивает пирамиду. - Решите неравенство
- www.itmathrepetitor.ru Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.
а) Докажите, что CO = KO.
б) Найдите отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет 9/100 площади трапеции ABCD. - В июле 2020 года планируется взять кредит в банке на некоторую сумму.
Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106964 рубля, то кредит будет полностью погашен за 2 года. Найдите r . - Найдите все значения
, при каждом из которых уравнение
имеет ровно один корень на отрезке ([0;1]).
- На доске написано 30 различных натуральных чисел, десятичная запись каждого из которых оканчивается или на цифру 2, или на цифру 6. Сумма написанных чисел равна 2454.
а) Может ли на доске быть поровну чисел, оканчивающихся на 2 и на 6?
б) Может ли ровно одно число на доске оканчиваться на 6?
в) Какое наименьшее количество чисел, оканчивающихся на 6, может быть на доске?
смотрите также Демо ЕГЭ 2017 Базовый уровень и ЕГЭ Реальный вариант № 337 Профильный уровень 2017
Ответы
- (скоро) и решение
Канал видеоролика: Виктор Осипов
Смотреть видео:
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:

Разбор Задания №14 из Варианта Ларина №278 ЕГЭ-2020.
Виктор Осипов

Разбор Задания №18 из Варианта Ларина №279 ЕГЭ-2020.
Виктор Осипов

Разбор Задания №16 из Варианта Ларина №278 ЕГЭ-2020
Виктор Осипов

Разбор Задания №15 из Варианта Ларина №279 ЕГЭ-2020.
Виктор Осипов
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
23.02.2020
- Комментарии
RSS
Написать комментарий
Нет комментариев. Ваш будет первым!
Ваше имя:
Загрузка…
ЕГЭ по математике, варианты № 301, 302, 303, 304, 305, 306, 11 класс, 2010.
Единый государственный экзамен по МАТЕМАТИКЕ Вариант № 301
Инструкция по выполнению работы
На выполнение экзаменационной работы по математике дается 4 часа (240 мин). Работа состоит из двух частей и содержит 18 заданий.
Часть 1 содержит 12 заданий с кратким ответом (B1—В12) базового уровня по материалу курса математики. Задания части 1 считаются выполненными, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби.
Часть 2 содержит 6 более сложных заданий (С1-С6) по материалу курса математики. При их выполнении надо записать полное решение и ответ.
Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
Ответом на задания B1—BI2 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов № I справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведенными в бланке образцами. Единицы измерений писать не нужно.
На рисунке жирными точками показана цена цинка на момент закрытия биржевых торгов во все рабочие дни с 5 по 18 февраля 2008 года. По горизонтали указываются числа месяца, по вертикали — цена тонны цинка в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку разность между наибольшей и наименьшей ценой цинка на момент закрытия торгов в указанный период (в долларах США за тонну).
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу ЕГЭ по математике, варианты № 301-306, 11 класс, 2010 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать книгу ЕГЭ по математике, вариант № 301-306, 11 класс, 2010
— pdf — Яндекс.Диск
Дата публикации: 25.09.2014 08:05 UTC
Теги:
ЕГЭ по математике :: 2010
Следующие учебники и книги:
- ЕГЭ 2015, математика, типовые тестовые задания, Высоцкий И.Р., Захаров П.И., Панферов В.С., Посицельский С.В., Семенов А.В., Семенова М.А., Сергеев И.Н., Смирнов В.А., Шестаков С.А., Шноль Д.Э., Ященко И.В., 2015
- ЕГЭ 2014, Математика, задача В8, Геометрический смысл производной, рабочая тетрадь, Ященко И.В., Захаров П.И.
- ЕГЭ 2014, Математика, Задача В6, Геометрия: углы на плоскости и в пространстве, рабочая тетрадь, Смирнов В.А.
- ЕГЭ 2014, Математика, Задача В2, Графики и диаграммы, рабочая тетрадь, Посицельская М.А., Посицельский С.Е.
Предыдущие статьи:
- ЕГЭ по математике, варианты № 521-536, 11 класс, 2010
- ЕГЭ по математике, варианты № 228-232, 237, 240, 248, 11 класс, 2010
- ЕГЭ по математике, варианты № 192-194, 199, 205, 209, 212, 11 класс, 2010
- ЕГЭ по математике, варианты № 101-190, критерии части С, 11 класс, 2010




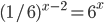

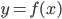
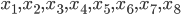

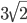
 Часть 2
Часть 2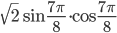
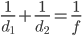
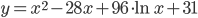
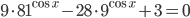
![[5pi/2;4pi]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_17546d5931b4e57add305efceb1df7a9.gif)