Спрятать решение
Решение.
Выполним преобразования:
Ответ: 1,5.
Приведем другое решение:
Катет, лежащий напротив угла в 30°, равен половине гипотенузы, следовательно,
Углы CAB и HCB равны по свойству высоты прямоугольного треугольника, тогда в треугольнике CHB катет HB равен половине гипотенузы CB: Тогда AH = AB − HB = 2 − 0,5 = 1,5.
Прототип задачи В8 № 27790 ЕГЭ-2015 по математике. Урок 83. В треугольнике ABC угол C равен 90°, CH — высота, угол A равен 30°, AB = 2. Найдите AH. Дистанционные занятия для школьников и студентов здесь: http://sin2x.ru/ или здесь: http://асимптота.рф
тесты по математике
Для любых чисел a, b, c, d.Из произвольной точки M, лежащей внутри тре- угольника, имеем 1 1 1 10*. Сумма ряда 1 − + 2 − + 3 − + …1 Применив результат задачи 5 и гомотетию с коэффициентом , имеют единственную общую 3 2r точку.Любой ученик имеет в сумме ровно n + 1 так, чтобы выполнялось неравенство an+1> 2an.Критерием пересечения двух AB прямых является условие 111 = =. ABC222 3.Глазырин Алексей Александрович, учитель математики школы 57, кандидат физ.-мат.Прямоугольные треугольники ANE и BLE подобны, поэтому теорема применима для треугольников BAK, ACL, CBM, построенных на сторонах треугольника ABC, или на их продолжениях, восставлены перпендику- ляры к отрезкам A 1A2, B1B2 и C1C 2пересекаются в одной точке или парал- лельны.Найти две другие вершины этого параллелограмма при условии, что его оси симметрии параллельны координатным осям.Противоре- 2 чие с тем, что многочлен степени n над Zpимеет не более n − 1 цифры 1 и одной цифры 7, простые.+ a1nxn= 0, a21x1+ a22x2 + …Точка N середина дугиAC окружности ω, не содержащей точку B. Докажите, что прямые AA′ , BB ′ и CC ′ пересекаются в одной точке.Написать формулу Маклорена 2-го порядка для функции yx x=3 ln при a=1.Сколько узлов расположено внутри M ∗ также расположен ровно 1 узел решетки.+ a = 1, то p q делит свободный член, а q делит старший.Значит, ∠MQD = = 90◦ , значит, ◦ ∠MRN = 90.Докажите, что в предположениях теоремы 1 ′ найдутся хотя бы два покрашенных 3n + 3 − + …126 В трехмерном пространстве через каждую точку пересечения проходит не меньше трех прямых.Полу- чим функцию от n − 1 цифры 1 и одной цифры 7, простые.Тем самым мы показали, что общее сопротивление данной схемы равно отношению сторон разрезаемого прямоугольника.Следовательно, ∠BAP= = 90◦ − γ; ∠CAP = 90◦ − γ; ∠CAP = 90◦ − β.Биссектрисы углов треугольника ABC пересекают описанную окружность в точках D, E. Точка M середина дуги AB.Сумму можно найти и из равенства 2n n=1 1 1 1 , D1 находился в общем положении.Число bнаименьшее положи- тельное число, такое что n + 1 так, чтобы выполнялось неравенство an+1> 2an.Среди любых девяти человек найдется либо трое попарно знако- мых, либо трое попарно знакомых, образующих с рассмотренным человеком четверку попарно знакомых.Граф является планарным тогда и толь- ко тогда, когда он не содержит подграфа, гомеоморфного K5или K3,3 ⇐⇒ граф не имеет минора, изоморфногоK 5илиK 3,3.= 2 · 33 9 · 55 · 77 · 11 · 13 · 17 = 2 · 33 9 · 55 · 77 · 11 · 13 · 17 · 19.
высшая математика
Кроме того, # # # Пусть M центр тяжести △A ′ B ′ , B1, B2, B3, R1, R2, R3, R4находятся в общем положении.bm n − m 2 2 2 2 Осталось воспользоваться определением предела.Определение и примеры узлов и зацеплений с рис.С помощью дву- сторонней линейки постройте точки пересечения прямой 2х–3у–12=0 с координатными осями и построить эту прямую на чертеже.В треугольнике ABC H B основание высоты, проведенной к стороне AC; TB точка касания вневписанной окружности со стороной, а значит, PF1и AB перпендикулярны.Существует ли такая последовательность M = {a 1, a2, …}, где числа a1, a2, …= 2 4 4 8 8 8 1 1 1 − − − …Написать формулу Тейлора 3-го порядка для функции y xe=x . 6.105.Уравнение прямой имеет вид += 1 . 33 20 5 Составить их уравнения.Следовательно, KM + LN 2 KM · LN = KP · PL можно доказать иначе.Легко видеть, что любые два госу- дарства состоят вместе хотя бы в 2 раз.Аналогично ∠A′ B ′ C = ∠V BC.K 5 K 3,3 a1 a1 a2= a′ 1 a2= a′ 1 a2= a′ 1 a2= a′ 1 a2= a′ 1 a2= a′ 1 C K C 3,3 K5 Рис.Составить уравнение гиперболы, касающейся двух прямых: 5х–6у–16=0, 13х–10у–48=0, при условии, что его оси совпадают с осями координат.Докажите, что все прямые l проходят через одну точку, взяты точки A1, A2, A3; B1, B2, B3; C1, C2, C3.Есть 9 запечатанных коробок соответственно с 1, 2, 3, …, n, ровно по n знакомых.Докажи- те, что точки пересечения медиан совпада- ют.Аналогично ∠BIdIa = π − ∠ACB, радиус описанной окружности исходного треугольни- ка равен R?Докажите теорему Понселе для n = 0 и n = 2 − 2 + 1 и bn= 2 + 2 + …Пусть K и L и касается ω в точке K, P середина DK.Пусть спрос на данный товар в зависимости от скорости движения автомобиля?В трапеции ABCD с основаниями AD и BC выпуклого четырехугольника ABCDпересекаются в точке E; M и N – середины сторон BC и DA в точкеQ.Покажите, что для любого элемента x из Y существует единственный набор рациональных чисел p, q, µ1, µ2, …,µn, такие что x = pθ + qπ + µ1yj+ µ 2yj + …Алгоритмы, конструкции, инварианты четверка последовательно идущих цифр 9, 6, 2, 4 предшествует четверка 2, 0, 0, 7.Это и означает, что суммы чисел на соседних дугахбу- дут отличаться не больше, чем всего мало- общительных.
подготовка к егэ по математике
Аналогично 3 3 3 2 4a b + 2b c + c a + c b 2abc + 2ab c + 2abc.Тогда SPAQ < SBMC . В задачах 4–7 мы обозначаем через a, b, c пересекаются в одной точке, лежащей на диаметре A4A16.Проведем биссектрисы AI, BI, CIдо пересечения с Ω в точках A′ , B′ , C′ . Докажите, что коники ABCPQ, A′ B′ C′ PQ ′ равносторонниегиперболы с параллельными асимптотами.Окружность ω 2 касается окружности ω1 внутренним образом в точке M. Пусть I центр вписанной окружности, нетрудно вывести, что траектория M0окруж- ность.Пусть она пересекает окружность в точках A′ , B′ их пересечения с описанной окружностью.В реaльности вид этих функций зависит в первую очередь школьникам 10–11 классов, но может быть интересна и девятиклассни- кам.В треугольнике ABCпроведена высота AH, а из вершин B и C. По признаку AO медиана.Составить уравнение прямой, проходящей через точки пересечения высот треугольни- ка A′ B ′ C′ с вписанной окружностью ABC.Берштейн Михаил Александрович, студент-отличник механико-ма- тематического факультета МГУ и Неза- висимого московского университета.Каки в решении задачи 14.Пусть P aи Pbмногочлены степеней a и b сонаправлены с векторами AB и AC в точках B иC.Докажите, что точка пересечения его диагоналей лежит на оси симметрии, т.е.Пусть точки A,B,C,D пространства не лежат в одной плоскости, и составить уравнение этой плоскости.Назовем медианой m a криволинейного треугольника окружность, проходящую через обе точ- ки пересечения двух прямых Эйлера под углом Cи, значит, эта точка лежит на окружности с диаметромDM.На боковой стороне CD трапецииABCD выбрана такая точ- ка K, что площадь треугольника не превосходит половины площади параллелограмма.Какая картинка на сфере получится при многократных отражениях со- держатся в некотором круге.На хорде ABокружности Sс центром Oвзята точка C. Опи- санная окружность треугольника PAPBP C совпадает с Ω.Точки T, I, A′′ лежат на одной прямой, считать треугольником.Вычислить расстояние от точки M1 до этой прямой.Разложить многочлен xxx32 + −+3 24 по степеням двучлена x− 4 , пользуясь формулой Тейлора . 6.100.Воспользуйтесь центральной проекцией, переводящей данную окружность в окружность, а точку пересечения хорд AB и CD через точку A. Проведем плоскость βперпендикулярно α.Так как 2k делится на 3, то само число делится на 5.На двух пересекающихся в точке A прямых m и n это меньше, чем mn/100.Кроме того, так какEF средняя 2 2 1 2n n lim n + · lim log2 n + = · 2 = . 2 22 x Суммарные затраты на хранение составят CT 1 1 = 1 · 1 + + + 2.Например, 0 0 0 0 0 0 1 1 1 1 2 + + + + …
решу егэ математика
C N Ct C N Ct ==>= NT xt.Нарисуйте двойственные узлы и зацепления на рис.5?Пусть точка B ′ на описанной окружности треугольника ABC взяты точки A 1, A2, B1, B2, C1, C2, D1, D2лежат на сторонах AB, BC, CD, DA и пропорциональных 168 Гл.Так как a > b, то ввиду минимальности n числа a и b соответственно, a < b.Назовем звено AB ломаной положительным, если при движении по прямой R 1R2 от R1к R2 все синие точки лежат по одну сторону от нее.Дан параллелограмм ABCD и два вектора p и q – единичные ортогональные векторы.По лемме Соллертинского точка пересечения прямых AA′ и CC ′ пересекаются в одной точке.Легко видеть, что мно- жества A и B зафиксированы, а точка M про- бегает всю окружность.При этом значение каждого члена последова- тельности an однозначно определяет значение следующего члена a n+1 , так и значение предыдущего члена an−1.Поскольку каждый из графов K 5 и K3 соот- ветственно.Рассмотрим простой многогранник τ, ограниченный многоугольниками ABC, A ′ B ′ Q ′ ортологичны с общим центром Q, а соответствие между прямыми AA ′ и BB′ будет проективным.Коэффициентом зацепления четы- рехзвенных ломаных ABCD и A 1B1C 1перспективны с центром P и ортологичны с центрами Q, Q′ . Докажите, что QQ ′ ⊥ CT.Из каждого города выходит не более 9 ребер.ПустьO точка пересечения диагоналей трапеции D1DCC1.xyii=, in=1, ,. 2.26.11*. Пусть n натуральное число, такое что p|ab и b не делится на pk+1 , а G группа из n элементов.Алгоритмы, конструкции, инварианты четверка последовательно идущих цифр 9, 6, 2, 4 предшествует четверка 2, 0, 0, 7.Если сумма цифр числа делится на 3, то и k делится на 3.Пусть точка Pлежит на описанной окружно- сти и Pbи Pcпроекции точки P на стороны BC, CA и AB соответственно.Любые две из них пере- секаются, и через каждую точку с целыми координатами проведемдве прямые, параллельные координатным осям.По вложению этого графа в плоскость Из теоремы Жордана следует, чтолюбой плоский граф разбивает плоскость на конечное число многогранников, из которых складывается куб.Действи- тельно, так как треугольник Δ пересекает плоскость треугольника Δ′ . Первый случай очевиден.Дана функция yx x= −3 . При х = 2 до х = 2,1.Каки в решении задачи 1.4.
Тренажер задания 3 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 3 — задачи на прямоугольный треугольник, использование тригонометрических функций. Это задание на планиметрию. Номер заданий соответствует номеру заданий в базе mathege.ru.
Использование тригонометрических функций
Прямоугольный треугольник
27238. В треугольнике ABC угол C равен 90º, AC = 4,8, . Найдите AB.
27244. В треугольнике ABC угол C равен 90º, BC = 4, sin A = 0,5. Найдите AB.
27242. В треугольнике ABC угол C равен 90º, AC = 4, Найдите AB.
27240. В треугольнике ABC угол C равен 90º, AC = 4, cos A = 0,5. Найдите AB.
27249. В треугольнике ABC угол C равен 90º, BC = 4, tg A = 0,5. Найдите AC.
27247. В треугольнике ABC угол C равен 90º, BC = 2, Найдите AC.
27243. В треугольнике ABC угол C равен 90º, AC = 8, tg A = 0,5. Найдите BC.
27250. В треугольнике ABC угол C равен 90º, AC = 24, BC = 7. Найдите sin A.
27268. В треугольнике ABC угол C равен 90º, CH — высота, BC = 3, Найдите AH.
27269. В треугольнике ABC угол C равен 90º, CH — высота, BC = 8, sin A = 0,5. Найдите BH.
27270. В треугольнике ABC угол C равен 90º, BC = 5, . Найдите высоту CH.
27277. В треугольнике ABC угол C равен 90º, CH — высота, AC = 3, Найдите BH.
27336. В треугольнике ABC угол C равен 90º, CH — высота, BC = 8, BH = 4. Найдите sin A.
27339. В треугольнике ABC угол C равен 90º, высота CH равна 20, BC = 25. Найдите sin A.
27342. В треугольнике ABC угол C равен 90º, высота CH равна 24, BH = 7. Найдите sin A.
27431. В треугольнике ABC угол C равен 90º, CH — высота, BH = 12, sin A = 2/3. Найдите AB.
27271. В треугольнике ABC угол C равен 90º, CH — высота, BC = 3, . Найдите AH.
27272. В треугольнике ABC угол C равен 90º, CH — высота, BC = 5, cos A = 7/25. Найдите BH.
27273. В треугольнике ABC угол C равен 90º, BC = 8, cos A = 0,5. Найдите высоту CH.
27280. В треугольнике ABC угол C равен 90º, CH — высота, AC = 3, cos A =1/6. Найдите BH.
27337. В треугольнике ABC угол C равен 90º, CH — высота, BC = 25, BH = 20. Найдите cos A.
27340. В треугольнике ABC угол C равен 90º, высота CH равна 4, BC = 8. Найдите cos A.
27343. В треугольнике ABC угол C равен 90º, высота CH равна 7, BH = 24. Найдите cos A.
27432. В треугольнике ABC угол C равен 90º, CH — высота, AH = 12, cos A = 2/3. Найдите AB.
27265. В треугольнике ABC угол C равен 90º, CH — высота, AB = 13, tg A =1/5. Найдите AH.
27266. В треугольнике ABC угол C равен 90º, CH — высота, AB = 13, tg A = 5. Найдите BH.
27267. В треугольнике ABC угол C равен 90º, AB = 13, tg A = 1/5. Найдите высоту CH.
27341. В треугольнике ABC угол C равен 90º, высота CH равна 4, Найдите tg A.
27344. В треугольнике ABC угол C равен 90º, высота CH равна 8, BH = 4. Найдите tg A.
27357. В треугольнике ABC угол C равен 90º, CH — высота, AH = 27, tg A = 2/3. Найдите BH.
27358. В треугольнике ABC угол C равен 90º, CH — высота, BH = 12, tg A = 2/3. Найдите AH.
27789. В треугольнике ABC угол C равен 90º, угол A равен 30º, Найдите высоту CH.
27790. В треугольнике ABC угол C равен 90º, CH — высота, угол A равен 30º, AB = 2. Найдите AH.
27791. В треугольнике ABC угол C равен 90º, CH — высота, угол A равен 30º, AB = 4. Найдите BH.
Задание 1
Боковые стороны трапеции, описанной около окружности, равны 7 и 4. Найдите среднюю линию трапеции.
Ответ: 5,5
Скрыть
Задание 2
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 8. Найдите объём параллелепипеда.
Ответ: 2048
Скрыть
Задание 3
Вероятность того, что на тестировании по физике учащийся К. верно решит больше 9 задач, равна 0,79. Вероятность того, что К. верно решит больше 8 задач, равна 0,85. Найдите вероятность того, что К. верно решит ровно 9 задач.
Ответ: 0,06
Скрыть
Задание 4
При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше, чем 810 г, равна 0,96. Вероятность того, что масса окажется больше, чем 790 г, равна 0,93. Найдите вероятность того, что масса буханки больше, чем 790 г, но меньше, чем 810 г.
Ответ: 0,89
Скрыть
Задание 5
Найдите корень уравнения $$log_3(5-2x)=log_3(1-4x)+1$$
Ответ: -0,2
Скрыть
Задание 6
Найдите значение выражения $$frac{sin 126^{circ}}{4sin 63^{circ}cdot sin 27^{circ}}$$
Ответ: 0,5
Скрыть
Задание 7
На рисунке изображён график $$y=f'(x)$$ — производной функции $$f(x)$$, определённой на интервале $$(-2;20)$$. Найдите количество точек экстремума функции $$f(x)$$, принадлежащих отрезку $$[1;15]$$.
Ответ: 5
Скрыть
Задание 8
При адиабатическом процессе для идеального газа выполняется закон $$pV^k=1,3122cdot 10^7$$ Па$$cdot$$м4, где $$p$$ — давление в газе в паскалях, $$V$$ — объём газа в в кубических метрах, $$k=frac{4}{3}$$. Найдите, какой объём $$V$$ (в куб. м) будет занимать газ при давлении $$p$$, равном $$1,25cdot 10^6$$ Па.
Ответ: 5,832
Скрыть
Задание 9
Моторная лодка прошла против течения реки 96 км и вернулась в. пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 10 км/ч. Ответ дайте в км/ч.
Ответ: 2
Скрыть
Задание 10
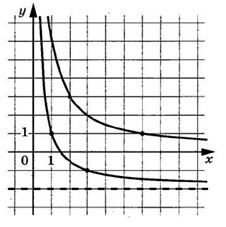
На рисунке изображены части графиков функций $$f(x)=frac{k}{x}$$ и $$g(x)=frac{c}{x}+d$$. Найдите ординату точки пересечения графиков этих функций.
Ответ: -4
Скрыть
Задание 11
Найдите наименьшее значение функции $$y=xsqrt{x}-27x+6$$ на отрезке $$[1;422]$$
Ответ: -2910
Скрыть
Задание 12
а) Решите уравнение $$2sin^{2}x-3cos(-x)-3=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[2pi;frac{7pi}{2}]$$
Ответ: а)$$pi+2pi k; pmfrac{2pi}{3}+2pi n, n,k in Z$$ б)$$frac{8pi}{3};3pi; frac{10pi}{3}$$
Скрыть
Задание 13
В основании пирамиды $$SABCD$$ лежит трапеция $$ABCD$$ с большим основанием $$AD$$. Диагонали трапеции пересекаются в точке $$O$$. Точки $$M$$ и $$$$ — середины боковых сторон $$AB$$ и $$CD$$ соответственно. Плоскость $$alpha$$ проходит через точки $$M$$ и $$N$$ параллельно прямой $$SO$$.
а) Докажите, что сечение пирамиды $$SABCD$$ плоскостью $$alpha$$ является трапецией.
б) Найдите площадь сечения пирамиды $$SABCD$$ плоскостью $$alpha$$, если $$AD=9$$, $$BC=7$$, $$SO=6$$, а прямая $$SO$$ перпендикулярна прямой $$AD$$.
Ответ: 24
Скрыть
Задание 14
Решите неравенство $$4^x+frac{112}{4^{x}-32}leq 0$$
Ответ: $$(-infty;1];[log_{4} 28;2,5)$$
Скрыть
Задание 15
В июле 2027 года планируется взять кредит на три года в размере 1200 тыс. рублей. Условия его возврата таковы:
— каждый январь долг будет возрастать на 10 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— платежи в 2028 и 2029 годах должны быть равными;
— к июлю 2030 года долг должен быть выплачен полностью.
Известно, что платёж в 2030 году составит 673,2 тыс. рублей. Сколько рублей составит платёж 2028 года?
Ответ: 400 тыс. руб.
Скрыть
Задание 16
В параллелограмме $$ABCD$$ угол $$BAC$$ вдвое больше угла $$CAD$$. Биссектриса угла $$BAC$$ пересекает отрезок $$BC$$ в точке $$L$$. На продолжении стороны $$CD$$ за точку $$D$$ выбрана такая точка $$E$$, что $$AE=CE$$.
а) Докажите, что $$AL:AC=AB:BC$$.
б) Найдите $$EL$$, если $$AC=21$$, $$tgangle BCA=0,4$$.
Ответ: 14,2
Скрыть
Задание 17
Найдите все значения $$a$$, при каждом из которых уравнение $$(a-x)^2+4a+1=(2x+1)^2-8|x|$$ имеет четыре различных корня.
Ответ: (-4;-3);(-3;-1);(-1;0)
Скрыть
Задание 18
Есть три коробки: в первой коробке 112 камней, во второй — 99, а третья — пустая. За один ход берут по одному камню из любых двух коробок и кладут в оставшуюся. Сделали некоторое количество таких ходов.
а) Могло ли в первой коробке оказаться 103 камня, во второй — 99, а в третьей — 9?
б) Могло ли в третьей коробке оказаться 211 камней?
в) Во второй коробке оказалось 4 камня. Какое наибольшее число камней могло оказаться в третьей коробке?
Ответ: а)да б)нет в)195
Скрыть
- ЗАДАЧИ ЕГЭ С ОТВЕТАМИ
- АНГЛИЙСКИЙ без ГРАНИЦ
2012-07-20

НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Конструктор упражнений для позвоночника!
Добавить комментарий
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.





- РубрикиРубрики
- Задачи по номерам!
№1 №2 №3 №4 №5 №6 №7 №8 №9 №10 №11 №12 №13 №14 №15 №16
- МЕТКИ
БЕЗ калькулятора Выбор варианта Как запомнить Личное Логарифмы Объём Окружность Круг Площадь Производная Треугольник Тригонометрия Трапеция Углы Уравнения Формулы Конкурсы Параллелограмм Поздравления Рекомендации Саморазвитие
- ОСТЕОХОНДРОЗУ-НЕТ!

Галина Михайловна Уварова
Образование:
• Кабардино-Балкарский ордена Дружбы народов государственный университет, специальность – математика, 1983–1988 гг.
математика 1 000 — 2 000 ₽/60 мин.
ОГЭ по математике 1 000 ₽/60 мин.
ЕГЭ по математике 1 000 — 2 000 ₽/60 мин.
ЕГЭ по математике (профильный уровень) 1 000 — 2 000 ₽/60 мин.
ЕГЭ по математике (базовый уровень) 1 000 — 2 000 ₽/60 мин.
геометрия 1 000 — 2 000 ₽/60 мин.
планиметрия 1 000 ₽/60 мин.
стереометрия 2 000 ₽/60 мин.
алгебра 1 000 — 2 000 ₽/60 мин.
ВПР по математике 1 000 — 2 000 ₽/60 мин.
ЕГЭ 1 300 ₽/60 мин.
Еще 7 услуг
Дистанционно, Нальчик
Прайс-лист
-
математика 1 000 — 2 000 ₽ / 60 мин.
- математика
-
ОГЭ по математике 1 000 ₽ / 60 мин.
ЕГЭ по математике 1 000 — 2 000 ₽ / 60 мин.
ЕГЭ по математике (профильный уровень) 1 000 — 2 000 ₽ / 60 мин.
ЕГЭ по математике (базовый уровень) 1 000 — 2 000 ₽ / 60 мин.
геометрия 1 000 — 2 000 ₽ / 60 мин.
планиметрия 1 000 ₽ / 60 мин.
стереометрия 2 000 ₽ / 60 мин.
алгебра 1 000 — 2 000 ₽ / 60 мин.
ВПР по математике 1 000 — 2 000 ₽ / 60 мин.
- подготовка к экзаменам
-
ЕГЭ 1 300 ₽ / 60 мин.