Задания
Версия для печати и копирования в MS Word
Тип 2 № 27157
Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
Спрятать решение
Решение.
При увеличении ребер в 3 раза площади треугольников, образующих грани октаэдра, увеличатся в 9 раз, поэтому суммарная площадь поверхности также увеличится в 9 раз.
Ответ: 9.
Аналоги к заданию № 27157: 76217 76219 76221 76223 76225 76227 76229 76231 76233 76235 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 5.3.3 Пирамида, её основание, боковые рёбра, высота, боковая поверхность
Классификатор планиметрии: Отношение длин, площадей, объемов подобных фигур, Подобие
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
27157 решу егэ математика
Не получается? Посмотреть ответ
Не получается? Посмотреть ответ
Не получается? Посмотреть ответ
Не получается? Посмотреть ответ
Не получается? Посмотреть ответ
Не получается? Посмотреть ответ
Не получается? Посмотреть ответ
Не получается? Посмотреть ответ
Не получается? Посмотреть ответ
Не получается? Посмотреть ответ
Не получается? Посмотреть ответ
Не получается? Посмотреть ответ
Не получается? Посмотреть ответ
Не получается? Посмотреть ответ
©Reshak. ru — сборник решебников для учеников старших классов. Здесь можно найти решебники, ГДЗ, переводы текстов по школьной программе. Практически весь материал, собранный на сайте — авторский с подробными пояснениями профильными специалистами. Вы сможете скачать гдз, решебники, улучшить школьные оценки, повысить знания, получить намного больше свободного времени.
Главная задача сайта: помогать школьникам и родителям в решении домашнего задания. Кроме того, весь материал совершенствуется, добавляются новые сборники решений.
Не получается.
Reshak. ru
25.06.2019 2:58:04
2019-06-25 02:58:04
Источники:
Http://reshak. ru/ege/math/17/ege. html
ЕГЭ–2022, математика базовый уровень: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 27157 решу егэ математика
27157 решу егэ математика
27157 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задания Д13 № 27157
Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
При увеличении ребер в 3 раза площади треугольников, образующих грани октаэдра, увеличатся в 9 раз, поэтому суммарная площадь поверхности также увеличится в 9 раз.
—>
Задания Д13 № 27157
За пи сы вай тесь на бес плат ное за ня тие.
Mathb-ege. sdamgia. ru
01.11.2018 4:23:49
2018-11-01 04:23:49
Источники:
Http://mathb-ege. sdamgia. ru/problem? id=27157
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 27157 решу егэ математика
27157 решу егэ математика
27157 решу егэ математика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 5 № 27157
Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
При увеличении ребер в 3 раза площади треугольников, образующих грани октаэдра, увеличатся в 9 раз, поэтому суммарная площадь поверхности также увеличится в 9 раз.
—>
Задание 5 № 27157
Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза.
Ege. sdamgia. ru
01.04.2020 13:55:16
2020-04-01 13:55:16
Источники:
Http://ege. sdamgia. ru/problem? id=27157

Меню
-
HomeГлавная страница -
ОбразованиеПроблемы и решения-
Домашнее обучение -
Как учиться -
Будущее образования -
Математическое образование -
Школьное образование -
Разное
-
-
ЕГЭПодготовка к экзамену
Аналогичные задания
Ответ
Здесь ответ
Элементарные задания
Меню
-
Элементарные заданияВ1, В2, В3, В4 -
Практико-ориентированные задачи -
Графики -
Выбор варианта
Алгебра +
Меню
-
Алгебра +В7, В11 -
Уравнения -
Преобразования
Производная
Меню
-
ПроизводнаяВ9, В15 -
Анализ графиков, касательная, скорость, первообразная -
Вычисление производной
Задачи
Меню
-
ЗадачиB6, B12, B14 -
Работа, движение, растворы, прогрессии -
Построение мат. моделей в физике и технике -
Теория вероятности, комбинаторика и статистика
Геометрия
Меню
-
Углы и треугольники -
4х-угольники. Многоугольники и окружности -
Площади. Вектора. Координаты -
Многогранники -
Тела вращения
Вход/Регистрация
Логин
Пароль
Запомнить меня
- Забыли пароль?
- Забыли логин?
- Регистрация

Проверить аттестат
Наверх
Тренажер задания 5 профильного ЕГЭ по математике-2022 (с ответами). Здесь приведены прототипы задания 5 — задачи на определение площади поверхности объемных фигур. Это задание на стереометрию. Номер заданий соответствует номеру заданий в базе mathege.ru.
Площади поверхности
Многогранники
27158. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
27215. Площадь поверхности тетраэдра равна 12. Найдите площадь поверхности многогранника, вершинами которого являются середины рёбер данного тетраэдра.
Куб
27055. Площадь поверхности куба равна 18. Найдите его диагональ.
27056. Объем куба равен 8. Найдите площадь его поверхности.
27139. Диагональ куба равна 1. Найдите площадь его поверхности.
27061. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
27130. Во сколько раз увеличится площадь поверхности куба, если все его рёбра увеличить в три раза?
27168. Объём первого куба в 8 раз больше объёма второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Призма
27057. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
27062. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
27148. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
27063. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
27132. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.
27151. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
27157. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
245356. Площадь поверхности правильной треугольной призмы равна 6. Какой станет площадь поверхности призмы, если все её рёбра увеличатся в три раза, а форма останется прежней?
245354. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
Пирамида
27131. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?
27172. Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?
Цилиндр
27058. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.
27133. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
245358. Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
284361. Площадь боковой поверхности цилиндра равна 2π, а диаметр основания — 1. Найдите высоту цилиндра.
284362. Площадь боковой поверхности цилиндра равна 2π, а высота — 1. Найдите диаметр основания.
Конус
27136. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующая увеличится в 3 раза, а радиус основания останется прежним?
27137. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней?
27160. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
Шар
27072. Дано два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
27163. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
Элементы 71—80 из 166.
Задача №:
27148. Прототип №: 27148
В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
Ответ:
Показать/скрыть правильный ответ
Задача №:
27151. Прототип №: 27151
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
Ответ:
Показать/скрыть правильный ответ
Задача №:
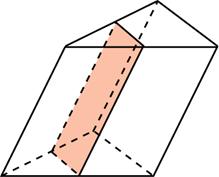
27153. Прототип №: 27153
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
Ответ:
Показать/скрыть правильный ответ
Задача №:
27158. Прототип №: 27158
Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
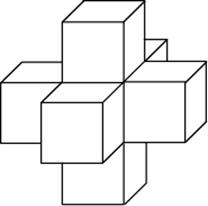
Ответ:
Показать/скрыть правильный ответ
Задача №:
27161. Прототип №: 27161
Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
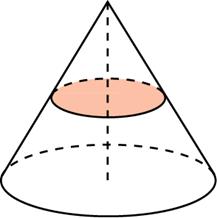
Ответ:
Показать/скрыть правильный ответ
Задача №:
27162. Прототип №: 27162
Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
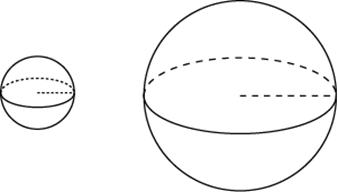
Ответ:
Показать/скрыть правильный ответ
Задача №:
27163. Прототип №: 27163
Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
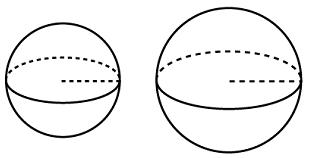
Ответ:
Показать/скрыть правильный ответ
Задача №:
27168. Прототип №: 27168
Объём первого куба в 8 раз больше объёма второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Ответ:
Показать/скрыть правильный ответ
Задание 8. Математика ЕГЭ. Найти радиус сферы описанного около конуса
Рубрика Задание 8, Решаем ЕГЭ по математике Комментарии (0)
Задание. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна 57√2. Найдите радиус сферы.
Решение:
Высота конуса равна радиусу сфере: h = R, L — образующая конуса.
По теореме Пифагора имеем:
h^2 + R^2 = L^2.
R^2 + R^2 = L^2
2·R^2 = L^2
2·R^2 = (57√2)^2
2·R^2 = 2·57^2
R^2 = 57^2
R = 57
Ответ: 57
Понравилось? Нажмите








