Егэ математика 2009 варианты - Помощь в подготовке к экзаменам и поступлению

Все варианты с реального ЕГЭ по математике 2009-2013 годов.

К сожалению, материалы предыдущих лет были удалены с файлообменника.
2012: 2012.pdf
2013: Скачать | критерии к части С: osn_center_krit.pdf

Варианты без ответов.

По отзывам выпускников в 2013 году варианты появились за несколько дней до экзамена в отличном качестве, а на самом ЕГЭ выяснилось, что они настоящие.

Рособрнадзор так и не признал утечку, сославшись на «сфальсифицированные продукты» и «мошеннические схемы».
http://obrnadzor.gov.ru/ru/press_center/news/index.php?id_4=2965
Дмитрий Ливанов утечку публично признал.

Источник ссылок на варианты — группа Вконтакте vk.com/pass2014exams

Источник

05.06.2009

Стали доступны для скачивания настоящие варианты ЕГЭ 2009 по математике. Данный материал может быть полезен для тех, кто будет сдавать ЕГЭ 2009 во второй волне. В заданиях можно увидеть основные типы задач, которые могут попастся на настоящем ЕГЭ по математике.

Материал публикуется уже после сдачи экзамена, и не имеет никакого отношения к конфликтной ситуации, связанной с публикацией настоящих вариантов ЕГЭ по математике во время экзамена 4 июня 2009 года.

СКАЧАТЬ Вариант 1 https://down.ctege.info/ege/2009/real/matem2009real-kim1.zip

СКАЧАТЬ Вариант 2 https://down.ctege.info/ege/2009/real/matem2009real-kim2.zip

Источник

Демонстрационный вариант ЕГЭ 2009 г.

МАТЕМАТИКА, 11 класс.

(2009 — 1 )

Проект

Единый государственный экзамен по МАТЕМАТИКЕ

Пояснения к демонстрационному варианту

При ознакомлении с Демонстрационным вариантом 2009 года следует иметь в виду, что задания, включённые в демонстрационный вариант, не отражают всех вопросов содержания, которые будут проверяться с помощью вариантов КИМ в 2009 году. Полный перечень вопросов, которые могут контролироваться на едином государственном экзамене 2009 года, приведен в кодификаторе элементов содержания по математике для составления контрольных измерительных материалов (КИМ) единого государственного экзамена 2009 г.

Назначение демонстрационного варианта заключается в том, чтобы дать возможность любому участнику ЕГЭ и широкой общественности составить представление о структуре будущих КИМ, количестве заданий, их форме, уровне сложности: базовом, повышенном и высоком. Приведённые критерии оценки выполнения заданий с развёрнутым ответом (тип «С»), включённые в этот вариант, позволят составить представление о требованиях к полноте и правильности записи развёрнутого ответа.

Эти сведения позволят выпускникам выработать стратегию подготовки и сдачи ЕГЭ в соответствии с целями, которые они ставят перед собой.

Для правильной распечатки файла демонстрационного варианта по математике необходимо установить на компьютере программное обеспечение MathType версии не ниже 5.0

Демонстрационный вариант ЕГЭ 2009 г.

МАТЕМАТИКА, 11 класс.

(2009 — 2 )

Единый государственный экзамен по МАТЕМАТИКЕ Демонстрационный вариант 2009 г.

Инструкция по выполнению работы

На выполнение экзаменационной работы по математике дается 4 часа (240 мин). Работа состоит из трех частей и содержит 26 заданий.

Часть 1 содержит 13 заданий (А1 – А10 и В1 – В3) обязательного уровня по материалу курса «Алгебра и начала анализа» 10-11 классов. К каждому заданию А1 – А10 приведены 4 варианта ответа, из которых только один верный. При выполнении этих заданий надо указать номер верного ответа. К заданиям В1 – В3 надо дать краткий ответ.

Часть 2 содержит 10 более сложных заданий (В4 – В11, С1, С2) по материалу курса «Алгебра и начала анализа» 10-11 классов, а также различных разделов курсов алгебры и геометрии основной и средней школы. К заданиям В4 – В11 надо дать краткий ответ, к заданиям С1 и С2

– записать решение.

Часть 3 содержит 3 самых сложных задания, два – алгебраических (С3, С5) и одно – геометрическое (С4). При их выполнении надо записать обоснованное решение.

За выполнение работы выставляются две оценки: аттестационная отметка и тестовый балл. Аттестационная отметка за усвоение курса алгебры и начал анализа 10-11 классов выставляется по пятибалльной шкале. При ее выставлении не учитывается выполнение четырех заданий (В9, В10, В11, С4). В тексте работы номера этих заданий отмечены звездочкой.

Тестовый балл выставляется по 100-балльной шкале на основе первичных баллов, полученных за выполнение всех заданий работы.

Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.

Желаем успеха!

Демонстрационный вариант ЕГЭ 2009 г.

МАТЕМАТИКА, 11 класс.

(2009 — 3 )

ЧАСТЬ 1

При выполнении заданий А1 – А10 в бланке ответов №1 под номером выполняемого задания поставьте знак «×» в клеточке, номер которой

соответствует номеру выбранного вами ответа.

A1				1,5
				11
	Упростите выражение	0,3 .

				11
	1)	1,2	2)	5	3)	111,2	4)	115
A2	Вычислите:	3 8 0,125.
	1)	1	2)	2	3)	2,5	4)	0,001
	Вычислите:	log3162 − log3 6.
A3
	1)	156	2)	27	3)	3	4)	52
		y = 2 x. Укажите
A4	На одном из рисунков изображен график функции

номер этого рисунка.

у			у
1)			2)
1			1	1
0	1	х	0	х

y			y
3)			4)
1				1
0	1	х	0	1	х

Демонстрационный вариант ЕГЭ 2009 г.	МАТЕМАТИКА, 11 класс.	(2009 — 4 )
Найдите производную функции	y =12x3 −e x .
1)	y′=15x 2 − xe x−1
2)	y′=3x 2 −	e x
x +1

3)	y′=36x 2 − xe x−1
4)	y′=36x 2 −e x

Найдите множество значений функции	y = 4 cos x.
1) [−1; 1]	2) [− 4; 4]	3) (− ∞; + ∞)	4) [0; 4]

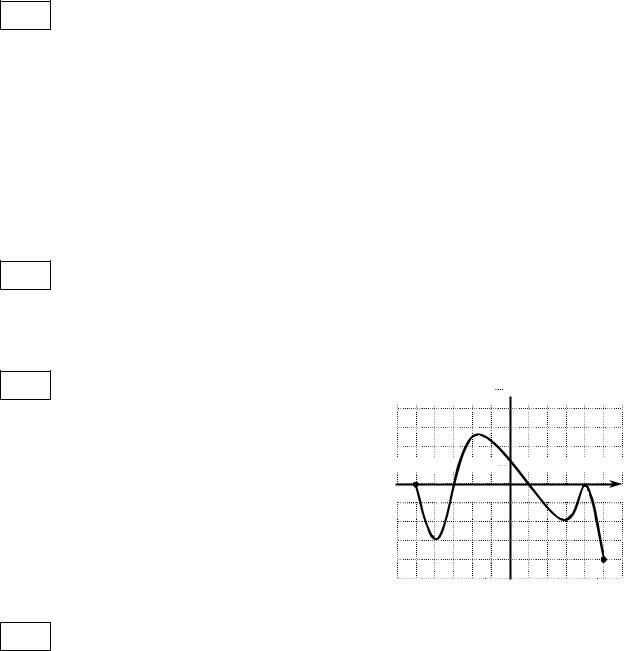
Функция задана графиком. Укажите промежуток, на котором она принимает только положительные значения.

1)(− 5; 0)

2)(− 3; 1)

3)(− 3; 4)

4)(− 5; 4)

Решите неравенство	5x	≥ 0.
4x − 8

1)	(− ∞; 0] (2; + ∞)
2)	[0;	2) (2; + ∞)
3)	[0;	2)

4) [0; + ∞)

Демонстрационный вариант ЕГЭ 2009 г.

МАТЕМАТИКА, 11 класс.

(2009 — 5 )

Решите уравнение 2sin x =1.

1)(−1)n π6 + πn, n Z

2)π2 + 2 πn, n Z

3)(−1)n+1 π6 + πn, n Z

4)−π2 + 2 πn, n Z

Решите неравенство	4 x − 2,7 >	1	.
64
1) (−5; + ∞)		(−∞; 0,3)	3) (−∞; −5,7 )	4) (−0,3; + ∞)
2)

Ответом на задания В1 – В11 должно быть некоторое целое число или число, записанное в виде десятичной дроби. Это число надо записать в бланк ответов №1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус отрицательного числа и запятую в записи десятичной дроби пишите в отдельной клеточке в соответствии с приведенными в бланке образцами. Единицы измерений писать не нужно.

Решите уравнение	8 3log3 x =13x −6 .
Решите уравнение	x 2 − 24 =1.

(Если уравнение имеет более одного корня, то в бланке ответов запишите меньший корень.)

B3 Найдите значение выражения 8cos2 α − 2sin 2 α, если sin α = − 0,2.

	Демонстрационный вариант ЕГЭ 2009 г.	МАТЕМАТИКА, 11 класс.	(2009 — 6 )
			ЧАСТЬ 2

B4	Решите уравнение	3x −6 (	3 )x − 27 = 0 .

(Если уравнение имеет более одного корня, то в бланке ответов запишите их произведение.)

Функция	у = f (x)	определена на		у
промежутке (– 6;	3).	На	рисунке


изображен	график	ее	производной.		у = f ′(x)



Укажите точку максимума	функции
	1

у = f (x) на промежутке (– 6;	3).






					–6	0 1	3 х

Вычислите значение выражения 8log8 6 + 625log 25 13 .

Найдите количество целочисленных решений неравенства

x	2 − 3x −10	≤ 0.
1 + 4 − x 2

B8 Функция y = f (x) определена на всей числовой прямой и является периодической с периодом 6. При − 2 ≤ x < 4 она задается формулой f (x )= x − 2 −3 . Найдите значение выражения 4 f (11) − 2 f (−15) .

B9 Секретарю фирмы поручили разослать письма адресатам по списку. Секретарь, отдав своему помощнику часть списка, содержащую 80% адресатов, взял оставшуюся часть себе и разослал письма по своей части списка за время, в 6 раз меньшее, чем помощник – по своей. Сколько процентов списка адресатов секретарь должен был сразу отдать помощнику (взяв себе остальные), чтобы они, работая с прежней производительностью, выполнили свою работу за одинаковое время?

Демонстрационный вариант ЕГЭ 2009 г.

МАТЕМАТИКА, 11 класс.

(2009 — 7 )

B10 Через образующую цилиндра AB проведены два сечения, пересекающие основание цилиндра: одно – по диаметру AM , другое – по хорде AD . Угол между плоскостями этих сечений равен 60°. Площадь боковой поверхности цилиндра равна 60π. Найдите площадь того из данных сечений цилиндра, которое проходит через хорду AD .

B11 В трапеции ABCD диагональ АС является биссектрисой угла А. Биссектриса угла В пересекает большее основание AD в точке Е. Найдите

высоту трапеции, если АС = 8 5 , ВЕ = 4 5 .

Для записи ответов на задания С1 и С2 используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем решение.

C1 Найдите наибольшее значение функции f (x) = х(2x −3)6

при x −1,5 ≤ 0,5.

C2	Найдите все значения х, при каждом из которых выражения
	sin 4x	и	cos4 x −sin 4 x	принимают равные значения.

	tg 2x	tg 2x

ЧАСТЬ 3

Для записи ответов на задания С3 – С5 используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем обоснованное решение.

C3	Найдите все значения x >1, при каждом из которых наибольшее из двух
	чисел a =log	2	x + 2log	x	32 − 2	и b = 41−log 2 x 2	больше 5.

				2

	Демонстрационный вариант ЕГЭ 2009 г.	МАТЕМАТИКА, 11	класс.	(2009 — 8 )

C4	В шар радиусом	11 вписана	правильная	треугольная призма
	АВСА1В1С1. Прямая АВ1 образует с плоскостью АСС1 угол 45°. Найдите
	объём призмы.

С5	Найдите все значения параметра p , при каждом из которых уравнение
	(1,5 p − 7) 320,4x +0,2	−	x	+11p − 41 = 0 имеет ровно

	+ (29 p −154) 0,125 3

10 p − p 2 −24 различных корней.

Демонстрационный вариант ЕГЭ 2009 г.

МАТЕМАТИКА, 11 класс.

(2009 — 9 )

Ответы к заданиям демонстрационного варианта по математике.

Ответы к заданиям с выбором ответа

№ задания	Ответ	№ задания	Ответ
А1	3	А6	2
А2	1	А7	2
А3	3	А8	1
А4	3	А9	1
А5	4	А10	4

Ответы к заданиям с кратким ответом

№ задания	Ответ
В1	1,2
В2	-5
В3	7,6
В4	4
В5	-3
В6	19
В7	5
B8	4
B9	40
В10	30
В11	8

Ответы к заданиям с развернутым ответом

№ задания				Ответ
С1					2
С2	(−1)	n		π	+	πn	, n Z.
		12	2
С3	1 < x <8,	x >32
С4					36
С5					6

Демонстрационный вариант ЕГЭ 2009 г.

МАТЕМАТИКА, 11 класс.

(2009 — 10 )

КРИТЕРИИ ПРОВЕРКИ И ОЦЕНКИ ВЫПОЛНЕНИЯ ЗАДАНИЙ С РАЗВЁРНУТЫМ ОТВЕТОМ

C1 Найдите наибольшее значение функции f (x) = х(2x −3)6

при x −1,5 ≤0,5.

Решение:

1)x −1,5 ≤ 0,5 −0,5 ≤ x −1,5 ≤ 0,5 1≤ x ≤ 2 .

2)f ′(x) =(2x −3)6 +12х(2x −3)5 =(2x −3)5 (14х−3). f ′(x) = 0 при x =1,5 , при x =143 .

143 [ 1;2].

f (1) =1, f (1,5) = 0 , f (2) = 2 .

Наибольшее значение функции y = f (x) на отрезке [1;2] равно 2.

Ответ: 2.
Баллы	Критерии оценки выполнения задания С1

Приведена верная последовательность всех шагов решения:

1) определен промежуток, на котором требуется найти наибольшее значение функции;

22) найдено наибольшее значение функции.

Все преобразования и вычисления выполнены верно. Получен верный ответ.

Приведена верная последовательность всех шагов решения. Допущены описка и/или вычислительная ошибка в шаге 2),

1не влияющие на дальнейший ход решения.1 В результате этой описки или ошибки может быть получен неверный ответ.

	0	Все случаи решения, которые не соответствуют вышеуказанным
	критериям выставления оценок в 1 и 2 балла.

1 Подробнее о выставлении 1 балла см. замечания к оценке выполнения заданий С1 во введении

к«Рекомендациям по оценке выполнения заданий с развернутым ответом (С1−С5) ».

Демонстрационный вариант ЕГЭ 2009 г. МАТЕМАТИКА, 11 класс. (2009 — 11 )

Найдите все значения х, при каждом из которых выражения

sin 4x

cos4 x −sin 4 x

принимают равные значения.

tg 2x

Решение:

cos 4 x −sin 4 x = sin 4x

cos 4 x −sin 4 x −sin 4x = 0.

tg 2x

(cos 4 x −sin 4 x )− 2 sin 2xcos 2x

cos 2x(1 − 2 sin 2x )

= 0

tg 2x

= 0

tg 2x

cos 2x(1 − 2 sin 2x )= 0

1 − 2 sin 2x

= 0

x =(−1)n

πn

, n Z.

cos 2x ≠ 0

sin 2x ≠ 0

Ответ: (

−1)n

+ πn , n Z.

Критерии оценки выполнения задания С2

Баллы

Приведена верная последовательность всех шагов решения: 1) составлено уравнение по условию задачи;

22) найдены корни полученного уравнения.

Все преобразования и вычисления выполнены верно. Получен верный ответ.

Приведена верная последовательность всех шагов решения. Допущена вычислительная ошибка или описка в шаге 2),

1не влияющие на правильность дальнейшего хода решения.

В результате этой ошибки или описки может быть получен неверный ответ.

	0	Все случаи решения, которые не соответствуют вышеуказанным
	критериям выставления оценок в 1 и 2 балла.

Демонстрационный вариант ЕГЭ 2009 г. МАТЕМАТИКА, 11 класс. (2009 — 12 )

Найдите все значения

x >1, при каждом из которых наибольшее из двух

чисел

a =log

x + 2log

32 − 2

и b = 41−log 2 x 2

больше

Решение:

Так как x >1, то

log 2 x > 0 .

log 2 x −7log

x +10

1) a >5 log

x +2log

32 −2 >5

log 2 x

(

log

x −2

)

(

log

x −5

)

> 0

log

x >5

x < 2.

log

2) b >5 41−log 2 x 2

>5 4log

2 x <36 log 2 x <9 log

x <3 .

a и

3) Наибольшее из чисел

больше 5 тогда и только тогда, когда

хотя бы одно из них больше 5, т.е. когда

a >5

log

x >5

x >32

log

x <3

x <8.

Ответ:

1 < x <8,

x >32.

Критерии оценки выполнения задания С3

Баллы

Приведено логически и арифметически верное решение, содержащее в каком-либо порядке и виде следующие шаги:

1) решение первого неравенства;

42) решение второго неравенства;

3)составление совокупности указанных двух неравенств и ее решение.

Получен верный ответ.

Приведено логически верное решение, содержащее шаги 1), 2) и 3). Получен ответ.

3Допустимы арифметические ошибки, в результате которых возможен неверный ответ.

Выполнены шаги 1) и 2) решения, а шаг 3) либо отсутствует, либо

2не доведен до конца, либо выполнен неверно. Ответ не получен или неверен.

		Верно выполнен один из шагов 1) или 2) решения, а остальные
	1	шаги либо отсутствуют, либо не доведены до конца, либо
	выполнены неверно.

		Ответ не получен или неверен.
		Все случаи решения, которые не соответствуют вышеуказанным

0критериям выставления оценок в 1 — 4 балла.

Демонстрационный вариант ЕГЭ 2009 г. МАТЕМАТИКА, 11 класс. (2009 — 13 )

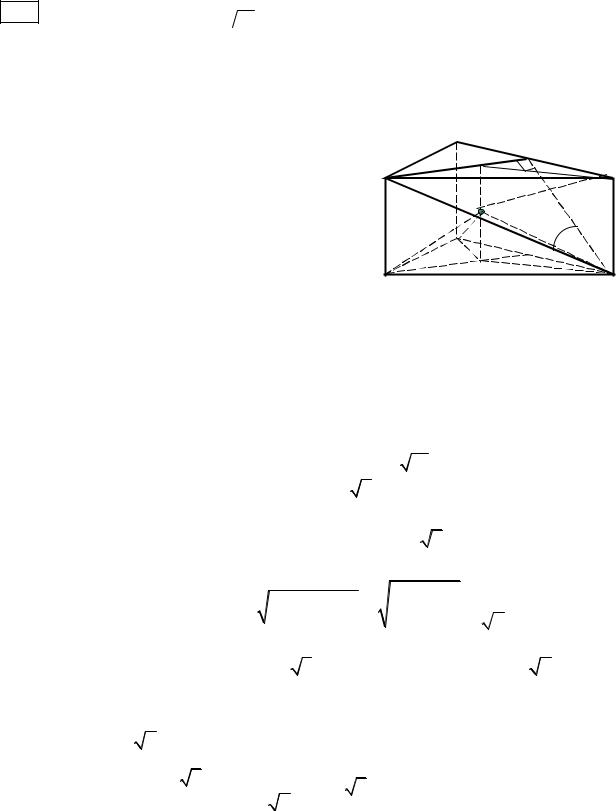
C4 В шар радиусом 11 вписана правильная треугольная призма АВСА1В1С1. Прямая АВ1 образует с плоскостью АСС1 угол 45°. Найдите объём призмы.

Решение:


1)	Пусть D1 – середина ребра А1С1.
Так призма правильная, то В1D1 А1С1
и	СС1 B1B D1, и	по	признаку
перпендикулярности	прямой	и
плоскости	В1D1 АСС1.	Значит,
В1АD1 = 45°	как угол между прямой

В1А и плоскостью АСС1.

	C1		D1
B1		М1
	A1

			О
	C		450

			М
B			A

2) Пусть М и М1 – центры оснований призмы, тогда АМ = ВМ = СМ и А1М1 = В1М1 = С1М1. Так как призма правильная, то ОМ АВС, где О – середина отрезка ММ1. Следовательно, по свойству наклонных и проекций ОА = ОВ = ОС и ОА1 = ОВ1 = ОС1. Так как ОМ = ОМ1 и АМ = А1М1, то прямоугольные треугольники ОМА и ОМ1А1 равны по двум катетам. Значит, ОА = ОА1. Следовательно, точка О равноудалена от всех вершин призмы АВСА1В1С1 и поэтому является центром описанного около

нее шара. Из условия радиус шара R = ОА =	11 .
3)	Пусть АВ = а.	Тогда	B D = a 3 .	Но		B1B D1A прямоугольный и
										1	1	2
В1АD = 45°. Следовательно, AB =		B1D1			= a		6 . Из АВВ1
	sin 45D
													1			2
					BB = AB2	− AB 2 =		3a 2		−a 2 =	a	.
							2
							1			1				2
4)	Отрезок MA = 2 B D =		a		,	отрезок		OM = 1 BB =		a		. Поэтому
			2	2
						3	1	1	3					2	1
	из прямоугольного	ОМА имеем				a 2		+	a 2	=11.	Следовательно,
			8
	a = 2														3
	6 . Объем призмы находим по формуле V = S ABC BB1 . Но
	S		=	a 2 3	,	BB	=		a	, a = 2 6 . Отсюда V = 36.

				2
		ABC	4			1

Ответ: 36.

Соседние файлы в папке МАТЕМАТИКА для экономистов

#
#
#
#
#
#
#
#
20.04.20159.11 Mб40Энциклопедия элементарной математики. 5. Геометрия. 1966.djvu

Источник

Название: ЕГЭ 2009. Математика. Сборник экзаменационных заданий.

Автор: Денищева Л.О., Рязановский А.Р., Семенов П.В., Сергеев И.Н.
2009

В издании представлено более 600 экзаменационных заданий частей А, В и С. Задания подготовлены официальным разработчиком контрольных измерительных материалов — Федеральным институтом педагогических измерений — и сгруппированы по экзаменационным темам, соответствующим кодификатору ЕГЭ по математике. По каждой теме предложены рекомендации и комментарии разработчиков заданий ЕГЭ, ко всем заданиям приведены ответы и критерии оценивания.
Книга адресована выпускникам средней школы и абитуриентам для подготовки к единому государственному экзамену по математике. Издание поможет учителям и репетиторам организовать эффективную подготовку учащихся к ЕГЭ.

В 2008 году заканчивается эксперимент по введению единого государственного экзамена (ЕГЭ), а с 2009 года для всех выпускников и желающих поступить в ВУЗы ЕГЭ станет обязательным. В ходе эксперимента на федеральном и региональном уровнях решались различные вопросы, связанные с процедурой проведения экзамена, поиском оптимальных экзаменационных моделей по общеобразовательным предметам, повышением качества контрольных измерительных материалов (КИМ).
В Российской Федерации созданием вариантов КИМ для ЕГЭ по 13 общеобразовательным предметам занимается только Федеральный институт педагогических измерений (ФЙПИ). Ежегодная процедура разработки КИМ состоит из нескольких этапов, в том числе многократного проведения внешней экспертизы отдельных тестовых заданий и целых вариантов. Все тестовые задания ЕГЭ хранятся в Федеральном банке экзаменационных материалов (ФБЭМ). Для пополнения банка тестовыми заданиями ежегодно организуется конкурс «Контрольные измерительные материалы и тестовые задания для единого государственного экзамена». Пополнение банка необходимыми тестовыми материалами осуществляется также на основе целевого заказа. В настоящее время в ФБЭМ находится более 100 000 заданий.

СОДЕРЖАНИЕ
Предисловие 3
Введение 5
ЭКЗАМЕНАЦИОННЫЕ ЗАДАНИЯ
1. Выражения и преобразования 7
1.1. Корень степени п 7
1.2. Степень с рациональным показателем 10
1.3. Логарифм 13
1.4. Тригонометрия 16
2. Уравнения и системы уравнений 21
2.1. Иррациональные уравнения 21
2.2. Показательные уравнения 23
2.3. Логарифмические уравнения 24
2.4. Тригонометрические уравнения 25
2.5. Комбинированные уравнения 32
2.6. Уравнения с параметром 36
2.7. Системы уравнений 39
3. Неравенства 42
3.1. Рациональные неравенства 42
3.2. Показательные неравенства 45
3.3. Логарифмические неравенства 48
3.4. Комбинированные неравенства 50
4. Функции 54
4.1. Область определения и область значений функции 54
4.2. Взаимное расположение графиков функций 64
4.3. Свойства функций: монотонность, четность, нечетность 67
4.4. Свойства функций, связанные с их графиками 69
4.5. Производная 97
4.6. Первообразная и площадь 106
4.7. Задания с развернутым ответом 108
5. Планиметрия 108
5.1. Треугольники 108
5.2. Параллелограмм 109
5.3. Трапеция 109
5.4. Трапеция и окружность 110
5.5. Правильные многоугольники 110
6. Стереометрия 111
6.1. Параллелепипед 111
6.2. Прямая треугольная призма 111
6.3. Прямая четырехугольная призма 112
6.4. Цилиндр. 113
6.5. Конус 114
6.6. Прямоугольный параллелепипед 114
6.7. Треугольная пирамида 115
6.8. Четырехугольная пирамида 117
КОММЕНТАРИИ
1. Выражения и преобразования 119
1.1. Корень степени п 120
1.2. Степень с рациональным показателем 121
1.3. Логарифм 123
1.4. Тригонометрия 126
2. Уравнения и системы уравнений 127
2.1. Иррациональные уравнения 127
2.2. Показательные уравнения 131
2.3. Логарифмические уравнения 133
2.4. Тригонометрические уравнения 139
2.5. Комбинированные уравнения 148
2.6. Уравнения с параметром 160
2.7. Системы уравнений 175
3. Неравенства 182
4. Функции 196
5. Решение стереометрических задач высокого уровня сложности 221
Ответы 243
Приложения 274
Приложение 1. Статистика выполнения заданий ЕГЭ по математике 274
Приложение 2. Сравнение результатов ЕГЭ по различным предметам в 2005, 2006, 2007 г 278

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:

Скачать книгу ЕГЭ 2009. Математика. Сборник экзаменационных заданий. Денищева Л.О., Рязановский А.Р., Семенов П.В., Сергеев И.Н. 2009 — fileskachat.com, быстрое и бесплатное скачивание.

Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу

Скачать книгу ЕГЭ 2009. Математика. Сборник экзаменационных заданий. Денищева Л.О., Рязановский А.Р., Семенов П.В., Сергеев И.Н. 2009 — depositfiles

Скачать книгу ЕГЭ 2009. Математика. Сборник экзаменационных заданий. Денищева Л.О., Рязановский А.Р., Семенов П.В., Сергеев И.Н. 2009 — letitbit

Дата публикации: 27.11.2011 08:53 UTC

Теги:

ЕГЭ по математике :: математика :: Денищева :: Рязановский :: Семенов :: Сергеев

Следующие учебники и книги:

Математика. Экспресс-репетитор для подготовки к ЕГЭ. Функции. Слонимская И.С., Слонимский Л.И., 2010
Математика. Экспресс-репетитор для подготовки к ЕГЭ. Решение текстовых задач. Слонимская И.С., Слонимский Л.И., 2010
Математика. Экспресс-репетитор для подготовки к ЕГЭ. Выражения и преобразования. Слонимская И.С., Слонимский Л.И., 2010
Математика. Функции. Тестовые задания В2, В8. Власова А.П., 2011

Предыдущие статьи:

ЕГЭ 2009. Математика. Сборник заданий. Кочагин В.В., Кочагина М.Н. 2009
ЕГЭ 2009. Математика. Репетитор. Кочагин В.В., Кочагина М.Н. 2009
ЕГЭ 2008. Математика. 11 класс. 60 вариантов тестовых заданий. 2008
Математика. Учимся решать задачи с параметром. Подготовка к ЕГЭ. Задание С5. Иванов С.О., Лысенко Ф.Ф., Кулабухов С.Ю., 2011

Источник

Название: Самое полное издание типовых вариантов реальных заданий ЕГЭ-2009. Математика.

Предлагаемый сборник позволяет сформировать представление об особенностях всех типов заданий, использующихся на ЕГЭ. В него вошли тренировочные варианты КИМ, составленные из заданий открытого сегмента Федерального банка тестовых заданий, размещенного на сайте ФИПИ. В сборнике содержатся ответы к заданиям тренировочных вариантов. В сборник также включена типовая инструкция для участников ЕГЭ, образцы бланков ответов и инструкции по их заполнению.

Данное пособие может быть использовано выпускниками для самостоятельной работы. С его помощью учащиеся XI классов могут проконтролировать уровень усвоения того или иного раздела школьной программы, потренироваться в выполнении заданий различной сложности.

Содержание

Предисловие. А. Г. ЕРШОВ. 5
ОФИЦИАЛЬНЫЕ ДОКУМЕНТЫ ЕГЭ
Правила для участников единого государственного экзамена. 6
Описание бланков регистрации и ответов участника ЕГЭ. 16
Правила заполнения бланков ответов ЕГЭ. 18
Образцы экзаменационных бланков. 32
ВАРИАНТЫ ЭКЗАМЕНАЦИОННЫХ РАБОТ
Инструкция по выполнению работы. 36
Вариант 1. 37
Часть 1. 37
Часть 2. 39
Часть 3. 40
Бланки ответов. 42
Вариант 2. 45
Часть 1. 45
Часть 2. 46
Часть 3. 48
Бланки ответов. 49
Вариант 3. 52
Часть 1. 52
Часть 2. 54
Часть 3. 55
Бланки ответов. 56
Вариант 4. 59
Часть 1. 59
Часть 2. 61
Часть 3. 62
Бланки ответов. 63
Вариант 5. 66
Часть 1. 66
Часть 2. 68
Часть 3. 69
Бланки ответов. 71
Вариант 6. 74
Часть 1. 74
Часть 2. 75
Часть 3. 77
Бланки ответов. 78
Вариант 7. 81
Часть 1. 81
Часть 2. 83
Часть 3. 84
Бланки ответов. 85
Вариант 8. 88
Часть 1. 88
Часть 2. 90
Часть 3. 91
Бланки ответов. 92
Вариант 9. 95
Часть 1. 95
Часть 2. 97
Часть 3. 98
Бланки ответов. 99
Вариант 10. 102
Часть 1. 102
Часть 2. 103
Часть 3. 105
Бланки ответов. 106
Вариант 11. 109
Часть 1. 109
Часть 2. 110
Часть 3. 112
Бланки ответов. 113
Вариант 12. 116
Часть 1. 116
Часть 2. 118
Часть 3. 119
Бланки ответов. 120
Ответы. 123

Предисловие

.
Формирование государственной системы объективного контроля качества образования является одной из актуальных задач, стоящих перед обществом и государством. К числу важнейших вопросов современной государственной политики в области образования относится обеспечение государственных гарантий реализации конституционных прав граждан на образование, прежде всего обеспечение равного доступа молодых людей к полноценному образованию.

С 2001 года на территории Российской Федерации проводится эксперимент по введению единого государственного экзамена (ЕГЭ) — новой формы государственной итоговой аттестации учащихся, результаты который засчитываются большинством ВУЗов. За семь лет проведения эксперимента было значительно улучшено качество контрольных измерительных материалов (КИМ), решены многие организационные проблемы. С 2009 года ЕГЭ как форма аттестации в соответствии с законодательством является обязательным.

Использование материалов сборника в педагогической практике позволит получить достаточно объективную информацию о состоянии общеобразовательной подготовки старшеклассников. Учителя школ и преподаватели структур доВУЗовской подготовки могут применить представленные варианты КИМ на этапе обобщения изученного материала и его повторения для выявления уровня подготовленности учащихся по предмету, их готовности к итоговой аттестации в форме ЕГЭ.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:

Скачать книгу Самое полное издание типовых вариантов реальных заданий ЕГЭ-2009. Математика. — fileskachat.com, быстрое и бесплатное скачивание.

Скачать djvu
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу

Скачать книгу — Самое полное издание типовых вариантов реальных заданий ЕГЭ-2009. Математика. — depositfiles

Скачать книгу — Самое полное издание типовых вариантов реальных заданий ЕГЭ-2009. Математика. — letitbit

Дата публикации: 28.11.2011 17:34 UTC

Теги:

ЕГЭ по математике :: типовые варианты :: 2009

Следующие учебники и книги:

ЕГЭ 2010, Математика, Типовые тестовые задания, Семенов, Ященко, 2010
ЕГЭ 2010. Математика. Тематические тренировочные задания. Кочагин В.В., Кочагина М.Н. 2009
ЕГЭ 2010. Математика. Сборник тренировочных работ. Семёнов А.Л., Ященко И.В. 2010
ЕГЭ 2010. Математика. Сборник заданий. Кочагин В.В., Кочагина М.Н. 2010

Предыдущие статьи:

ЕГЭ 2010. Математика. Репетитор. Кочагин В.В., Кочагина М.Н. 2009
ЕГЭ 2010. Математика. Задача С5. Козко А.И., Панферов В.С., Сергеев И.Н., Чирский В.Г. 2010
ЕГЭ 2010. Математика. Задача С4. Гордин Р.К. 2010
ЕГЭ 2010. Математика. Задача С3. Сергеев И.Н., Панферов В.С. 2010

Источник

Ответы к заданиям с выбором ответа

Ответы к заданиям с кратким ответом

Ответы к заданиям с развернутым ответом

Новое и интересное на сайте: