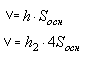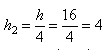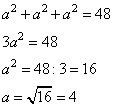Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 4 часа раньше, чем велосипедист приехал в A, а встретились они через 50 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
Спрятать решение
Решение.
Примем расстояние между городами 1. Пусть время движения велосипедиста равно x ч, тогда время движения мотоциклиста равно ч,
К моменту встречи они находились в пути 50 минут и в сумме преодолели всё расстояние между городами, поэтому
Таким образом, велосипедист находился в пути 5 часов.
Ответ: 5.
Задание 2. Информатика. Апробация 10.03.2023
Миша заполнял таблицу истинности логической функции (F)
$$
(x to neg (y to z)) lor w,
$$
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных (w), (x), (y), (z).
| F | ||||
| 0 | 0 | 0 | ||
| 1 | 0 | |||
| 0 | 1 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных (w), (x), (y), (z).
В ответе напишите буквы (w), (x), (y), (z) в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Функция (F) задана выражением ( neg x lor y), зависящим от двух переменных, а фрагмент таблицы имеет следующий вид:
В этом случае первому столбцу соответствует переменная (y), а второму — переменная (x). В ответе следует написать: (yx).
Решение:
Python
from itertools import permutations, product
def F(x, y, z, w):
return (x <= (not y <= z)) or w
for perm in permutations('xyzw'):
for a,b,c,d,e,f,g in product([0,1], repeat=7):
table = [[a,0,b,0,0],
[1,c,d,e,0],
[0,1,f,g,0]]
if table[0] == table[1]:
continue
if all(F(**dict(zip(perm,row))) == row[-1] for row in table):
print(*perm)
Ответ: (yzxw)
Тренировочная работа №3 статград ЕГЭ 2022 по математике 11 класс задания и ответы для вариантов МА2110301, МА2110302, МА2110303, МА2110304, МА2110305, МА2110306, МА2110307, МА2110308, МА2110309, МА2110310, МА2110311, МА2110312. Официальная дата проведения работы: 16.02.2022 (16 февраля 2022 год).
Скачать варианты статград базы ЕГЭ 2022
Скачать варианты статград профиль ЕГЭ 2022
Все ответы (решения) и задания (без водяного знака)
Тренировочные варианты статград базового уровня ЕГЭ 2022 по математике 11 класс задания и ответы:
Тренировочные варианты статград профильного уровня ЕГЭ 2022 по математике 11 класс задания и ответы:
Некоторые задания с варианта МА2110301:
2)Для покраски 1 кв. м потолка требуется 150 г краски. Краска продаётся в банках по 2,5 кг. Какое наименьшее количество банок краски нужно для покраски потолка площадью 41 кв. м?
4)В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России с 1 сентября 2013 года. Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 77 км/ч на участке дороги с максимальной разрешённой скоростью 40 км/ч? Ответ дайте в рублях.
5)План местности разбит на клетки. Каждая клетка обозначает квадрат 1м×1м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
6)Держатели дисконтной карты книжного магазина получают при покупке скидку 5 %. Книга стоит 240 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
10)Дачный участок имеет форму прямоугольника, стороны которого равны 40 м и 50 м. Дом, расположенный на участке, имеет на плане форму квадрата со стороной 9 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах.
11)В чемпионате по гимнастике участвуют 65 спортсменок: 18 из Аргентины, 21 из Бразилии, остальные — из Парагвая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Парагвая.
12)На соревнованиях по прыжкам в воду судьи выставили оценки от 0 до 10 трём спортсменам. Результаты приведены в таблице. Итоговый балл вычисляется следующим образом: две наибольшие и две наименьшие оценки отбрасываются, а три оставшиеся складываются, и их сумма умножается на коэффициент сложности. В ответе укажите номера спортсменов, итоговый балл которых больше 170, без пробелов, запятых и других дополнительных символов.
13)Высота бака цилиндрической формы равна 40 см, а площадь его основания равна 150 квадратным сантиметрам. Чему равен объём этого бака (в литрах)? В одном литре 1000 кубических сантиметров.
16)Объём конуса равен 48π , а его высота равна 9. Найдите радиус основания конуса.
18)Каждый раз, когда Надя приезжает в деревню к бабушке в гости, бабушка заплетает ей косички. Также Надя заплетает себе косички всегда, когда идёт на физкультуру. Выберите утверждения, которые верны при приведённых условиях. 1) Каждый раз, когда у Нади заплетены косички, она находится в деревне. 2) Если Надя без косичек, значит, она не у бабушки в гостях. 3) Если Надя без косичек, значит, сегодня физкультура. 4) Когда Надя сдаёт норматив по бегу на физкультуре, она с косичками.
19)Найдите пятизначное число, кратное 18, любые две соседние цифры которого отличаются на 2. В ответе укажите какое-нибудь одно такое число.
20)Из двух городов, расстояние между которыми равно 270 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 55 км/ч и 80 км/ч?
21)Взяли несколько досок и распилили их. Всего сделали 9 поперечных распилов, в итоге получилось 17 кусков. Сколько досок взяли?
Некоторые задания с варианта МА2110302:
1)Для покраски 1 кв. м потолка требуется 230 г краски. Краска продаётся в банках по 2 кг. Какое наименьшее количество банок краски нужно для покраски потолка площадью 44 кв. м?
4)В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России с 1 сентября 2013 года. Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 182 км/ч на участке дороги с максимальной разрешённой скоростью 100 км/ч? Ответ дайте в рублях.
6)Держатели дисконтной карты книжного магазина получают при покупке скидку 10 %. Книга стоит 210 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
7)Найдите значение выражения − ° 15cos630 .
10)Дачный участок имеет форму квадрата, сторона которого равна 40 м. Дом, расположенный на участке, имеет на плане форму прямоугольника, стороны которого равны 9 м и 8 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах.
11)В чемпионате по гимнастике участвуют 50 спортсменок: 21 из Сербии, 14 из Хорватии, остальные — из Словении. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Словении.
13)Высота бака цилиндрической формы равна 50 см, а площадь его основания равна 140 квадратным сантиметрам. Чему равен объём этого бака (в литрах)? В одном литре 1000 кубических сантиметров.
16)Объём конуса равен 84π , а его высота равна 7. Найдите радиус основания конуса.
18)В 9 «Б» классе география по расписанию по средам и пятницам. Каждый ученик должен приносить атлас на каждый урок географии. На других уроках атлас не требуется. Выберите утверждения, которые верны при приведённых условиях. 1) Всякий день, когда ученик 9 «Б» класса берёт с собой в школу атлас, является пятницей. 2) В среду Маше из 9 «Б» класса надо принести в школу атлас. 3) По четвергам ученикам 9 «Б» класса не надо брать в школу географический атлас. 4) В каждый день, отличный от среды, ученикам 9 «Б» класса атлас можно в школу не брать.
19)Найдите пятизначное число, кратное 25, любые две соседние цифры которого отличаются на 2. В ответе укажите какое-нибудь одно такое число.
20)Из двух городов, расстояние между которыми равно 420 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?
21)Взяли несколько досок и распилили их. Всего сделали 6 поперечных распилов, в итоге получилось 15 кусков. Сколько досок взяли?
Некоторые задания с варианта МА2110305:
2)Установка двух счётчиков воды (холодной и горячей) стоит 3400 рублей. До установки счётчиков за воду платили 2100 рублей ежемесячно. После установки счётчиков ежемесячная оплата воды стала составлять 1400 рублей. Через какое наименьшее количество месяцев экономия по оплате воды превысит затраты на установку счётчиков, если тарифы на воду не изменятся?
4)На рисунке показано изменение атмосферного давления в течение трёх суток. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Определите по рисунку наименьшее значение атмосферного давления (в миллиметрах ртутного столба) в четверг.
6)Магазин детских товаров закупает погремушки по оптовой цене 240 рублей за одну штуку и продаёт с наценкой 35 %. Сколько рублей будут стоить 2 такие погремушки, купленные в этом магазине?
10)От столба высотой 12 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба равно 12 м. Найдите длину провода. Ответ дайте в метрах.
11)Помещение освещается двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,2. Найдите вероятность того, что в течение года обе лампы перегорят.
13)Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка в четыре раза выше второй, а вторая в полтора раза ýже первой. Во сколько раз объём второй коробки меньше объёма первой?
15)На окружности отмечена точка C. Отрезок AB — диаметр окружности, AC = 8, BC =15 . Найдите радиус окружности.
16)Объём конуса равен 32π , а его высота равна 6. Найдите радиус основания конуса.
18)Маша младше Алисы на год, но старше Кати на два года. Выберите утверждения, которые верны при указанных условиях. 1) Любая девочка, помимо указанных, которая старше Кати, также старше Маши. 2) Среди указанных девочек нет никого младше Кати. 3) Любая девочка, помимо указанных, которая старше Маши, также старше Кати. 4) Алиса и Катя одного возраста.
19)Найдите четырёхзначное число, кратное 55, все цифры которого различны и чётны. В ответе укажите какое-нибудь одно такое число.
20)Двое рабочих, работая вместе, могут выполнить работу за 6 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за 1 день выполняет такую же часть работы, какую второй — за 2 дня?
21)В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 3345. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённым по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; 2,8 — до 3.)
Некоторые задания с варианта МА2110306:
2)Установка двух счётчиков воды (холодной и горячей) стоит 3500 рублей. До установки счётчиков за воду платили 2400 рублей ежемесячно. После установки счётчиков ежемесячная оплата воды стала составлять 1500 рублей. Через какое наименьшее количество месяцев экономия по оплате воды превысит затраты на установку счётчиков, если тарифы на воду не изменятся?
6)Магазин детских товаров закупает погремушки по оптовой цене 120 рублей за одну штуку и продаёт с наценкой 25 %. Сколько рублей будут стоить 3 такие погремушки, купленные в этом магазине?
10)От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба равно 15 м. Найдите длину провода. Ответ дайте в метрах.
11)Помещение освещается двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года обе лампы перегорят.
13)Даны две коробки, имеющие форму правильной четырёхугольной призмы, стоящей на основании. Первая коробка в полтора раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
15)На окружности отмечена точка C. Отрезок AB — диаметр окружности, AC = 7 , BC = 24. Найдите радиус окружности.
16)Объём конуса равен 75π , а его высота равна 9. Найдите радиус основания конуса.
18)Кошка Китти весит на 3 килограмма больше кошки Машки, а кошка Лада на полтора килограмма легче кошки Машки. Выберите утверждения, которые верны при указанных условиях. 1) Любая кошка, помимо указанных, которая весит меньше Лады, весит также меньше Китти. 2) Любая кошка, помимо указанных, которая весит меньше Китти, весит также меньше Лады. 3) Среди указанных кошек нет кошек тяжелее Китти. 4) Машка весит меньше Лады.
19)Найдите четырёхзначное число, кратное 88, все цифры которого различны и чётны. В ответе укажите какое-нибудь одно такое число.
20)Двое рабочих, работая вместе, могут выполнить работу за 6 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за 5 дней выполняет такую же часть работы, какую второй — за 3 дня?
21)В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 2097. Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2», «3», «4» или «5» и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округлённым по правилам округления? (Например, 3,2 округляется до 3; 4,5 — до 5; 2,8 — до 3.)
Некоторые задания с варианта МА2110309:
2)Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 36 теннисистов, среди которых 8 спортсменов из России, в том числе Юрий Молчанов. Найдите вероятность того, что в первом туре Юрий Молчанов будет играть с каким-либо теннисистом из России.
3)В треугольнике ABC угол C равен 62° , AD и BE — биссектрисы, пересекающиеся в точке O . Найдите угол AOB. Ответ дайте в градусах.
5)Стороны основания правильной шестиугольной пирамиды равны 24, боковые рёбра равны 37. Найдите площадь боковой поверхности этой пирамиды.
6)На рисунке изображён график функции y f’ x = ( ) — производной функции f x( ), определённой на интервале ( −2; 9). В какой точке отрезка [−1; 3] функция f x( ) принимает наибольшее значение?
8)Первый и второй насосы, работая совместно, наполняют бассейн за 24 минуты, второй и третий — за 35 минут, а первый и третий — за 40 минут. За сколько минут эти три насоса, работая совместно, заполнят бассейн?
10)Платежный терминал в течение рабочего дня может выйти из строя. Вероятность этого события 0,07. В торговом центре независимо друг от друга работают два таких платёжных терминала. Найдите вероятность того, что хотя бы один из них в течение рабочего дня будет исправен.
13)Основанием пирамиды SABCD является квадрат ABCD . Высота пирамиды проходит через точку D , М — середина бокового ребра SC . Угол между прямыми АМ и ВС равен 60° . а) Докажите, что SD CD : 11 = . б) Найдите расстояние от точки D до плоскости ABS , если сторона основания пирамиды равна 2 33 .
15)По вкладу «А» банк в конце каждого года планирует увеличивать на 7 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 6 % в первый год и на целое число n процентов во второй год. Найдите наименьшее значение n , при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных вкладов.
18)На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 264. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71). а) Могла ли сумма получившихся чисел быть ровно в 4 раза больше, чем сумма исходных чисел? б) Могла ли сумма получившихся чисел быть ровно в 3 раза больше, чем сумма исходных чисел? в) Найдите наибольшее возможное значение суммы получившихся чисел.
Некоторые задания с варианта МА2110310:
2)Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 шахматистов, среди которых 10 спортсменов из России, в том числе Александр Ефимов. Найдите вероятность того, что в первом туре Александр Ефимов будет играть с каким-либо шахматистом из России.
3)В треугольнике ABC угол C равен 138° , AD и BE — биссектрисы, пересекающиеся в точке O . Найдите угол AOB. Ответ дайте в градусах.
5)Стороны основания правильной шестиугольной пирамиды равны 18, боковые рёбра равны 41. Найдите площадь боковой поверхности этой пирамиды.
8)Первый и второй насосы, работая совместно, наполняют бассейн за 180 минут, второй и третий — за 210 минут, а первый и третий — за 280 минут. За сколько минут эти три насоса, работая совместно, заполнят бассейн?
10)Платежный терминал в течение рабочего дня может выйти из строя. Вероятность этого события 0,04. В торговом центре независимо друг от друга работают два таких платёжных терминала. Найдите вероятность того, что хотя бы один из них в течение рабочего дня будет исправен.
15)По вкладу «А» банк в конце каждого года планирует увеличивать на 9 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 7 % в первый год и на целое число n процентов во второй год. Найдите наименьшее значение n , при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных вкладов.
18)На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 165. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71). а) Могла ли сумма получившихся чисел быть ровно в 4 раза больше, чем сумма исходных чисел? б) Могла ли сумма получившихся чисел быть ровно в 5 раз больше, чем сумма исходных чисел? в) Найдите наибольшее возможное значение суммы получившихся чисел.
Некоторые задания с варианта МА2110311:
2)Конкурс исполнителей проводится в 4 дня. Всего заявлено 60 выступлений: по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 6 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что выступление исполнителя из России состоится в третий день конкурса?
3)Найдите угол ACB , если вписанные углы ADB и DAE опираются на дуги окружности, градусные меры которых равны соответственно 98° и 32° . Ответ дайте в градусах.
5)Диагональ куба равна 13. Найдите площадь полной поверхности куба.
6)На рисунке изображён график функции y f’ x = ( ) — производной функции f x( ), определённой на интервале ( −10;12). Найдите количество точек минимума функции f x( ), принадлежащих отрезку [−9;10].
8)Первый велосипедист выехал из посёлка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 14 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 3 часа после этого догнал первого. Ответ дайте в км/ч.
10)Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 45 % этих стёкол, вторая –– 55 %. Среди стекол, произведенных на первой фабрике, 3 % имеют дефекты. Вторая фабрика выпускает 1 % дефектных стекол. Все стекла поступают в продажу в магазины запчастей. Найдите вероятность того, что случайно выбранное стекло окажется с дефектом.
13)Основанием пирамиды SABCD является квадрат ABCD . Высота пирамиды проходит через точку D , М — середина бокового ребра SC . Угол между прямыми АМ и ВС равен 30° . а) Докажите, что CD SD : 3 = . б) Найдите расстояние от точки D до плоскости ABS , если сторона основания пирамиды равна 6.
15)По вкладу «А» банк в конце каждого года планирует увеличивать на 8 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 6 % в первый год и на целое число n процентов во второй год. Найдите наименьшее значение n , при котором за два года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных вкладов.
18)На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 429. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71). а) Могла ли сумма получившихся чисел быть ровно в 4 раза больше, чем сумма исходных чисел? б) Могла ли сумма получившихся чисел быть ровно в 3 раза больше, чем сумма исходных чисел? в) Найдите наибольшее возможное значение суммы получившихся чисел.
Другие тренировочные варианты статград ЕГЭ по математике 11 класс:
Работы СТАТГРАД по математике задания и ответы
Статград пробный ЕГЭ 2022 по математике 11 класс варианты МА2110201-МА2110212 с ответами
Метки: ЕГЭ 2022заданияматематика 11 классответыстатградтренировочная работа
ЕГЭ математика — База 2023. Открытый банк заданий с ответами.
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Тренировочные варианты ЕГЭ 2023 по математике (профиль)
| vk.com/pezhirovschool | |
| Вариант 1 | решения |
| Вариант 2 | решения |
| Вариант 3 | решения |
| Вариант 4 | решения |
| Вариант 5 (с ответами) | |
| Вариант 6 (с ответами) | |
| Вариант 7 (с ответами) | |
| Вариант 8 (с ответами) | |
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| вариант 12 | скачать |
| вариант 13 | скачать |
| вариант 14 | скачать |
| вариант 15 | скачать |
| вариант 16 | скачать |
| вариант 17 | скачать |
| вариант 18 | скачать |
| вариант 19 | скачать |
| вариант 20 | скачать |
| time4math.ru | |
| вариант 1-2 | ответы |
| вариант 3-4 | ответы |
| вариант 5-6 | ответы |
| вариант 7-8 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2023-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2023-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2023-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2023-yagubov-prof-var36 |
| вариант 37 (январь) | ege2023-yagubov-prof-var37 |
| вариант 38 (февраль) | ege2023-yagubov-prof-var38 |
| math100.ru (с ответами) | |
| variant 179 | скачать |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| variant 189 | скачать |
| variant 190 | скачать |
| variant 191 | скачать |
| variant 192 | скачать |
| variant 193 | скачать |
| variant 194 | скачать |
| variant 195 | скачать |
| variant 196 | скачать |
| variant 197 | скачать |
| variant 198 | скачать |
| variant 199 | скачать |
| variant 200 | скачать |
| variant 201 | скачать |
| variant 202 | скачать |
| variant 203 | скачать |
| variant 204 | скачать |
| variant 205 | скачать |
| alexlarin.net | |
| Вариант 397 | проверить ответы |
| Вариант 398 | проверить ответы |
| Вариант 399 | проверить ответы |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| Вариант 406 | проверить ответы |
| Вариант 407 | проверить ответы |
| Вариант 408 | проверить ответы |
| Вариант 409 | проверить ответы |
| Вариант 410 | проверить ответы |
| Вариант 411 | проверить ответы |
| Вариант 412 | проверить ответы |
| Вариант 413 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| вариант 8 | скачать |
| вариант 9 | скачать |
| вариант 10 | скачать |
| вариант 11 | скачать |
| vk.com/math.studying | |
| Вариант 1 | ответы |
| vk.com/marsel_tutor | |
| Вариант 1 | разбор |
| Вариант 2 | конспект / разбор |
| Вариант 3 | конспект / разбор |
| Вариант 4 | конспект / разбор |
| Вариант 5 | конспект / разбор |
| Вариант 6 | разбор |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
| Вариант 6 | решение |
| vk.com/mathlearn_ru | |
| вариант 1 | разбор |
| vk.com/ekaterina_chekmareva | |
| Вариант 1 | ответы |
| Вариант 2 | ответы |
| Вариант 3 | ответы |
| Вариант 4 | ответы |
| Вариант 5 | ответы |
| Вариант 6 | ответы |
| Вариант 7 | ответы |
| Вариант 8 | ответы |
Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня
Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.
Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов.
Примеры заданий:
1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.
2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу
3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.
Смотрите также:
В летнем лагере на каждого участника полагается 40 г сахара в день. В лагере 106 человек. Какое наименьшее количество килограммовых упаковок сахара нужно на весь лагерь на 7 дней?
В летнем лагере на каждого участника полагается 20 г сахара в день. В лагере 115 человек. Какое наименьшее количество килограммовых упаковок сахара нужно на весь лагерь на 5 дней?
На бензоколонке один литр бензина стоит 46 руб. 20 коп. Водитель залил в бак 30 литров бензина и взял бутылку воды за 41 рубль. Сколько рублей сдачи он должен получить с 1500 рублей?
На автозаправке клиент отдал кассиру 1500 рублей и попросил залить бензин до полного бака. Цена бензина 46 рублей за литр. Клиент получил 212 рублей сдачи. Сколько литров бензина было залито в бак?
Спидометр автомобиля показывает скорость в милях в час. Какую скорость (в милях в час) показывает спидометр, если автомобиль движется со скоростью 120 км в час? (Считайте, что 1 миля равна 1,6 км.)
Спидометр автомобиля показывает скорость в милях в час. Какую скорость (в милях в час) показывает спидометр, если автомобиль движется со скоростью 100 км в час? (Считайте, что 1 миля равна 1,6 км.)
Принтер печатает одну страницу за 8 секунд. Какое наибольшее количество страниц можно напечатать на этом принтере за 14 минут?
Стоимость проездного билета на месяц составляет 1150 рублей, а стоимость билета на одну поездку – 40 рублей. Аня купила проездной и сделала за месяц 37 поездок. На сколько рублей больше она бы потратила, если бы каждый раз покупала билет на одну поездку?
Стоимость проездного билета на месяц составляет 655 рублей, а стоимость билета на одну поездку – 25 рублей. Аня купила проездной и сделала за месяц 47 поездок. На сколько рублей больше она бы потратила, если бы каждый раз покупала билет на одну поездку?
Бегун пробежал 150 метров за 18 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.
Профильный уровень переход на базовый уровень
РЕШЕНИЯ ЕГЭ ПО МАТЕМАТИКЕ — 2013
на нашем сайте
Копирование решений на другие сайты запрещено.
Вы можете поставить ссылку на эту страницу.
Наша система тестирования и подготовки к экзамену РЕШУ ЕГЭ РФ.
Наши справочные материалы для подготовки к экзамену.
Внимание! Мы не стремились привести самые короткие или самые красивые решения: каждый имеет право решать задачу так, как ему проще: одним удобнее за несколько минут заполнить страницу выкладками, другие предпочитают подумать, но получить короткое решение. Для аналогичных задач мы старались различные решения. Среди 2400 приведенных решений есть, конечно, и решения с опечатками. Заметите — сообщайте. Удачи!
C 2001 по 2009 год в России начался эксперимент по объединению выпускных экзаменов из школ со вступительными экзаменами в высшие учебные заведения. В 2009 году этот эксперимент был закончен, и с тех пор единый государственный экзамен стал основной формой контроля школьной подготовки.
В 2010 году на смену старой команде составителей экзамена пришла новая. Вместе с разработчиками изменилась и структура экзамена: уменьшилось число задач, увеличилось количество геометрических задач, появилась задача олимпиадного типа.
Важным нововведением стала подготовка открытого банка экзаменационных заданий, в котором разработчики разместили около 75 тысяч заданий. Решить эту бездну задач никто не в силах, но это и не нужно. В действительности, основные типы заданий, представлены так называемыми прототипами, их примеро 2400 штук. Все остальные задачи получены из них при помощи компьютерного клонирования; они отличаются от прототипов только конкретными числовыми данными.
Продолжая наши традиции мы представляем вашему вниманию решения всех прототипов экзаменационных заданий, существующих в открытом банке. После каждого прототипа приводится список составленных на его основе задач-клонов для самостоятельных упражнений.
Всё варианты 13 задания математика ЕГЭ Профиль 2020admin2020-08-06T14:25:33+03:00
Скачать задания в формате pdf.
Комментарии для сайта Cackle
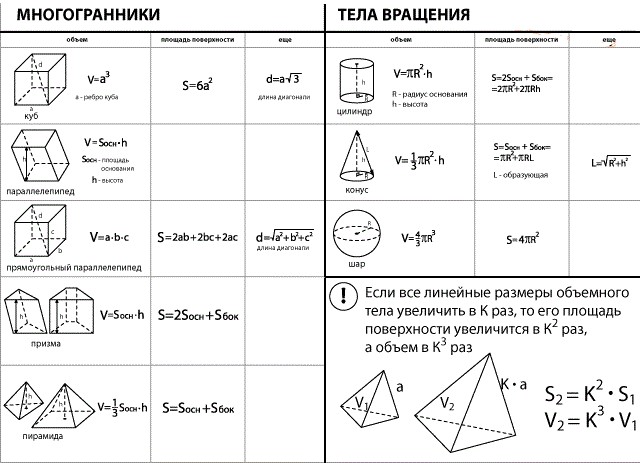
Стереометрия
Задание №8 в профильном уровне ЕГЭ по математике проверяет базовые знания стереометрии. Задания в этом разделе простые, на базовые формулы – обычно на объемы простых стандартных фигур – цилиндра, куба, пирамиды, конуса.
Теория к заданию №8
Приведу формулы объема фигур, так данный материал довольно часто встречается.
Разбор типовых вариантов заданий №8 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого? Ответ выразите в см.
Алгоритм решения:
- Определяем площадь основания первого и второго сосудов.
- Записываем формулы объемов и приравниваем их.
- Убираем одинаковые величины. Делаем вывод.
- Записываем ответ.
Решение:
1. Площадь основания первого сосуда определяется формулой
Диаметр второго сосуда в 2 раза больше. Значит площадь основания его равна
то есть в 4 раза больше:
2 Записываем формулы объема жидкости в каждом сосуде.
Так как объем жидкости остается постоянным, получаем уравнение:
Убираем одинаковые величины. Отсюда
Ответ: 4.
Второй вариант задания (из Ященко, №1)
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 28. Найдите объём цилиндра.
Алгоритм решения:
- Записываем формулу объема конуса.
- Записываем формулу объема цилиндра.
- Сравниваем формулы, делаем вывод.
- Вычисляем объем цилиндра.
- Записываем ответ.
Решение:
1. Объем конуса определяем по формуле
где H – высота конуса; R – радиус основания конуса.
2. Объем цилиндра определяем по формуле
3. Сравниваем обе формулы. Легко видно, что объем цилиндра в 3 раза больше объема конуса.
4. Вычисляем объем цилиндра::
Ответ: 84.
Третий вариант задания (из Ященко)
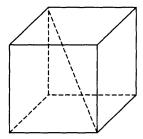
Диагональ куба равна . Найдите его объём.
Алгоритм решения:
- Выражаем диагональ куба, используя теорему Пифагора.
- Решаем полученное уравнение.
- Вычисляем объем.
- Записываем ответ.
Решение:
1. По тереме Пифагора диагональ грани куба определяется формулой:
Тогда диагональ куба
2. Отсюда
3. Объем куба равен
Ответ: 64.
Даниил Романович | Просмотров: 27.1k | Оценить: