Задание 1
Решите уравнение $$(frac{3}{2})^{2x}cdotsqrt[6]{frac{729}{7}}=sqrt[3]{7^{-5x}}$$
Ответ: -0,5
Скрыть
После преобразований:
$$(frac{3}{7^{frac{1}{6}}})^{2x+1}=1$$
$$2x+1=0$$
$$x=−0,5$$
Задание 2
В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. 18 мая погода в Волшебной стране хорошая. Найдите вероятность того, что 21 мая в Волшебной стране будет отличная погода.
Ответ: 0,392
Скрыть
Пусть $$O$$ – отличная погода, $$X$$ – хорошая
Всего четыре возможных варианта на 19,20,21 числа
$$XXO, XOO,OOO,OXO$$
$$P(A_1+A_2+A_3+A_4)=P(A_1)+P(A_2)+P(A_3)+P(A_4)=$$
$$=0,8cdot0,8cdot0,2+0,8cdot0,2cdot0,8+0,2cdot0,8cdot0,8+0,2cdot0,2cdot0,2=0,392$$
Задание 3
Найдите угол АСВ, если вписанные углы ADB и DAE опираются на дуги окружности, градусные меры которых равны соответственно 118° и 38°. Ответ дайте в градусах.
Ответ: 40
Скрыть
$$angle ADB=frac{138}{2}=59,$$ тогда $$angle CDA=180−59=121$$
$$angle DAE=frac{38}{2}=19$$
$$ACB=180−121−19=40$$
Задание 4
Найдите значение выражения $$log_{sqrt{a}}(bcdotsqrt[4]{a})+log_{sqrt{b}}a+log_asqrt{ab},$$ если $$log_{a^2b}frac{b}{a}=frac{1}{4}$$
Ответ: 7
Скрыть
$$2(log_a b+log_a a^{frac{1}{4}})+2log_b a+0,5(log_a a+log_a b)=$$
$$=2log_a b+0,5+frac{2}{log_a b}+0,5+0,5log_a b$$
Пусть $$log_a b=t$$
Тогда перепишется
$$2t+frac{2}{t}+0,5t+1$$
Перейдем к тому, что дано
$$log_{a^2b}frac{b}{a}=frac{1}{4}$$
$$frac{log_afrac{b}{a}}{log_a a^2b}=frac{1}{4}$$
$$frac{t−1}{t+2}=14$$
$$t=2$$
Подставляем и получаем ответ 6
Задание 5
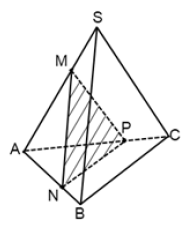
Объем пирамиды SABC равен 54. На ребрах SA, АВ и АС взяты точки М, N и Р соответственно так, что SM:MA=BN:NA=CP:PA=1:2. Найдите объем пирамиды MANP.
Ответ: 16
Скрыть
$$V_{SABC}=frac{1}{3}S_{ABC}h=54$$
$$Delta ABC$$ подобен $$Delta ANP$$ по 2-м углам
$$k=frac{3}{2}$$
$$S_{ANP}=frac{S_{ABC}}{k^2}=frac{4}{9}S_{ABC}$$
$$Delta AMO_1$$ подобен $$Delta ASO$$
$$frac{MO_1}{SO}=frac{2}{3}$$
$$MO_1=frac{2}{3}h$$
$$V_{MANP}=frac{1}{3}cdotfrac{4}{9}cdot S_{ABC}cdotfrac{2}{3}h$$
Из условия $$V_{SABC}=54$$ можно легко найти объем 16
Задание 6
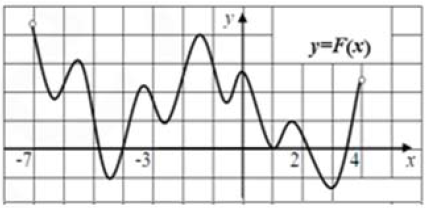
На рисунке изображён график функции $$y=F(x)$$ — одной из первообразных некоторой функции $$f(x),$$ определённой на интервале $$(-7;4).$$ Пользуясь рисунком, определите значение функции $$f(x)$$ в точке $$x=0.$$
Ответ: 0
Скрыть
$$F'(x)=f(x)$$
Можно заметить, что точка $$x=0$$ — точка локального максимума функции
По геометрическому смыслу производной:
$$F'(0)=k=tgalpha=0$$
Задание 7
Кинетическая энергия тела, имеющего массу $$m$$ (кг) и скорость $$v$$ (м/с) равна $$E=frac{mv^2}{2}$$ (Дж). Какую наименьшую начальную скорость должна иметь пуля массой 9 граммов, чтобы при прохождении через неподвижную мишень передать ей энергию не меньше 810 Дж, уменьшив при этом свою скорость не более чем в три раза? (Считать, что в процессе полёта пули потери энергии не происходит). Ответ дайте в м/с.
Ответ: 450
Скрыть
$$frac{mv^2_0}{2}=frac{mv^2}{2}+810$$
$$v=frac{v_0}{3}$$
Откуда
$$v_0=450$$
Задание 8
На круговой дорожке стадиона длиной 400 м тренируются два спортсмена, совершая забег из одной точки дорожки. Найдите скорость в м/сек движения каждого из них, если известно, что при движении в одну сторону они встречаются каждые 20/3 минуты, а при движении в противоположные стороны они встречаются каждые 4/3 минуты. В ответе укажите произведение полученных значений.
Ответ: 6
Скрыть
$$T_1=frac{20}{3}$$ минуты или 400 с
$$T_2=frac{4}{3}$$ минуты или 80 с
$$T_1V_1−T_1V_2=400$$
$$T_2V_1+T_2V_2=400$$
Откуда $$V_1=3 V_2=2$$
$$2cdot3=6$$
Задание 9
На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Ответ: -1,25
Скрыть
Уравнение прямой $$y=kx+b$$
$$k=tgalpha$$
Легко найти из рисунка из прямоугольных треугольников, также легко найти коэффициент $$b$$ из рисунка или из уравнения
$$f(x)=2,5x+1,5$$
$$g(x)=-1,5x-3,5$$
Найдем точку пересечения:
$$2,5x+1,5=-1,5x−3,5$$
$$x=-1,25$$
Задание 10
Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 3. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых.
Ответ: 0,42
Скрыть
В первом броске нас устраивает только очки: $$1,2,3,$$ если будет больше то бросать перестанем
$$A_1$$ Во-втором броске, если при первом броске выпало $$1,$$ то нас устраивает $$3,4,5,6,$$ чтобы перестать бросать дальше
$$A_2$$ Во-втором броске, если при первом броске выпало $$2,$$ то нас устраивает $$2,3,4,5,6$$
$$A_3$$ Во-втором броске, если при первом броске выпало $$3,$$ то нас устраивает $$1,2,3,4,5,6$$
$$P=frac{1}{6}cdotfrac{4}{6}+frac{1}{6}cdotfrac{5}{6}+frac{1}{6}cdotfrac{6}{6}approx0,42$$
Задание 11
Найдите наименьшее значение функции $$f(x)=(x^2-8x+8)cdot e^{2-x}$$ на отрезке $$[1;7].$$
Ответ: -4
Скрыть
Найдем критические точки: $$(2x−8)e^{2−x}−(x^2−8x+8)e^{2−x}=0$$
$$e^{2−x}(2x−8−x^2+8x−8)=0$$
$$e^{2−x}neq0$$
$$−x^2+10x−16=0$$
$$x=2$$ - точка минимума
$$x=8$$ — точка максимума
$$y(2)=−4$$
Задание 12
А) Решите уравнение $$frac{tg3x}{1+cos3x}=cos3x-1$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-frac{pi}{2};frac{5pi}{6}]$$
Ответ: А)$$frac{2pi n}{3},nin Z$$ Б)$$0;frac{2pi}{3}$$
Задание 13
Основанием правильной треугольной пирамиды МАВС является треугольник АВС со стороной 6. Ребро МА перпендикулярно грани МВС. Через вершину пирамиды М и середины ребер АС и ВС проведена плоскость $$alpha.$$
А) Докажите, что сечение пирамиды плоскостью $$alpha$$ является равносторонним треугольником.
Б) Найдите расстояние от вершины С до плоскости $$alpha.$$
Ответ: $$sqrt{6}$$
Задание 14
Решите неравенство: $$log_{x+8}(x^2-3x-4)<2cdotlog_{(4-x)^2}|x-4|$$
Ответ: $$(-8;-7),(-2;-1),(4;5),(5;6)$$
Задание 15
В растворе Х содержится 30% вещества А и 50% вещества В, в растворе Y содержится 50% вещества А и 40% вещества В, в растворе Z содержится 80% вещества А и 10% вещества В. В результате смешивания получился раствор, содержащий 60% вещества А. Найдите наименьшее возможное содержание вещества В в получившемся растворе.
Ответ: 26%
Задание 16
Дана окружность с диаметром АВ. Вторая окружность с центром в точке А пересекает первую окружность в точках С и D и диаметр в точке Е. На дуге СЕ, не содержащей точки D, взята точка М, отличная от точек С и Е. Луч ВМ пересекает первую окружность в точке N, а вторую пересекает вторично в точке К.
А) Докажите, что MN=NK
Б) Найдите MN, если известно, что CN=2, ND=3.
Ответ: $$sqrt{6}$$
Задание 17
Найдите все значения параметра $$a,$$ при каждом из которых неравенство
$$frac{sqrt{6+x-x^2}}{x-2a}leqfrac{sqrt{6+x-x^2}}{2x-2a+4}$$
имеет ровно два решения
Ответ: $$(-infty;-1),(5;infty)$$
Задание 18
Участники конкурса на лучшую математическую задачу анонимно присылают каждый свою задачу. После публикации все участники дают оценку каждой задаче, кроме своей. В конкурсе принимают участие 6 человек. Каждый участник за лучшую по его мнению задачу дает 5 баллов, за следующую — 4 балла и так далее, за пятую — 1 балл. По каждой задаче баллы суммируются, так определяется рейтинг задачи.
А) Могут ли все рейтинги быть простыми числами?
Б) Могла ли сумма четырех наибольших рейтингов быть в три раза больше суммы остальных?
В) Какова минимальная сумма третьего и четвертого рейтингов, если им дали номера в порядке невозрастания?
Ответ: А) да, Б) нет, В) 22
А. Ларин. Тренировочный вариант № 372.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Основанием правильной треугольной пирамиды MABC является треугольник ABC со стороной 6. Ребро MA перпендикулярно грани MBC. Через вершину пирамиды M и середины ребер AC и BC проведена плоскость α.
а) Докажите, что сечение пирамиды плоскостью α является равносторонним треугольником.
б) Найдите расстояние от вершины C до плоскости α.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В растворе Х содержится 30% вещества А и 50% вещества В, в растворе Y содержится 50% вещества А и 40% вещества В, в растворе Z содержится 80% вещества А и 10% вещества В. В результате смешивания получился раствор, содержащий 60% вещества А. Найдите наименьшее возможное содержание вещества В в получившемся растворе.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
Дана окружность с диаметром AB. Вторая окружность с центром в точке A пересекает первую окружность в точках C и D и диаметр в точке E. На дуге CE, не содержащей точки D, взята точка M, отличная от точек C и E. Луч BM пересекает первую окружность в точке N, а вторую пересекает вторично в точке K.
а) Докажите, что MN = NK.
б) Найдите MN, если известно, что CN = 2, ND = 3.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра a, при каждом из которых неравенство
имеет ровно два решения.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Участники конкурса на лучшую математическую задачу анонимно присылают каждый свою задачу. После публикации все участники дают оценку каждой задаче, кроме своей. В конкурсе принимают участие 6 человек. Каждый участник за лучшую по его мнению задачу дает 5 баллов, за следующую — 4 балла и так далее, за пятую — 1 балл. По каждой задаче баллы суммируются, так определяется рейтинг задачи.
а) Могут ли все рейтинги быть простыми числами?
б) Могла ли сумма четырех наибольших рейтингов быть в три раза больше суммы остальных?
в) Какова минимальная сумма третьего и четвертого рейтингов, если им дали номера в порядке невозрастания?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Тренировочный вариант №372 Алекса Ларина ЕГЭ 2022 по математике профильный уровень 11 класс с ответами и решением по новой демоверсии ЕГЭ 2022 года для подготовки к экзамену, дата выхода варианта: 11.12.2021 (11 декабря 2021 года)
Скачать вариант Ларина
Ответы для варианта
Решать вариант Алекса Ларина №372 ЕГЭ 2022 по математике:
2)В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. 18 мая погода в Волшебной стране хорошая. Найдите вероятность того, что 21 мая в Волшебной стране будет отличная погода.
Ответ: 0,392
3)Найдите угол АСВ, если вписанные углы АDВ и DАЕ опираются на дуги окружности, градусные меры которых равны соответственно 118° и 38°. Ответ дайте в градусах.
Ответ: 40
4)Объем пирамиды SABC равен 54. На ребрах SA, АВ и АС взяты точки М, N и Р соответственно так, что SM:MA= =BN:NA=CP:PA=1:2. Найдите объем пирамиды МАNP.
Ответ: 7
8)На круговой дорожке стадиона длиной 400 м тренируются два спортсмена, совершая забег из одной точки дорожки. Найдите скорость в м/сек движения каждого из них, если известно, что при движении в одну сторону они встречаются каждые 20/3 минуты, а при движении в противоположные стороны они встречаются каждые 4/3 минуты. В ответе укажите произведение полученных значений.
Ответ: 6
9)На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Ответ: -1,25
10)Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 3. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых.
Ответ: 0,42
15)В растворе Х содержится 30% вещества А и 50% вещества В, в растворе Y содержится 50% вещества А и 40% вещества В, в растворе Z содержится 80% вещества А и 10% вещества В. В результате смешивания получился раствор, содержащий 60% вещества А. Найдите наименьшее возможное содержание вещества В в получившемся растворе.
Ответ: 26%
16)Дана окружность с диаметром АВ. Вторая окружность с центром в точке А пересекает первую окружность в точках С и D и диаметр в точке Е. На дуге СЕ, не содержащей точки D, взята точка М, отличная от точек С и Е. Луч ВМ пересекает первую окружность в точке N, а вторую пересекает вторично в точке К. А) Докажите, что MN=NK Б) Найдите MN, если известно, что CN=2, ND=3.
Ответ: б-корень из 6
18)Участники конкурса на лучшую математическую задачу анонимно присылают каждый свою задачу. После публикации все участники дают оценку каждой задаче, кроме своей. В конкурсе принимают участие 6 человек. Каждый участник за лучшую по его мнению задачу дает 5 баллов, за следующую – 4 балла и так далее, за пятую – 1 балл. По каждой задаче баллы суммируются, так определяется рейтинг задачи.
Ответ: а-да, б-нет, в-22
Смотрите также другие варианты Ларина ЕГЭ 2022:
-
Вариант Ларина №370 ЕГЭ 2022 по математике профиль с ответами
-
Вариант Ларина №371 ЕГЭ 2022 по математике профиль с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
На чтение 1 мин Просмотров 1 Опубликовано 5 марта, 2023
Вариант Ларина №372 ЕГЭ 2022 по математике профиль с ответами Решение и ответы на задачи на официальном сайте источника онлайн.
Тренировочный вариант №372 Алекса Ларина ЕГЭ 2022 по математике профильный уровень 11 класс с ответами и решением по новой демоверсии
Варианты ответов и решение задачи ТУТ: https://100ballnik.com/%d0%b2%d0%b0%d1%80%d0%b8%d0%b0%d0%bd%d1%82-%d0%bb%d0%b0%d1%80%d0%b8%d0%bd%d0%b0-%e2%84%96372-%d0%b5%d0%b3%d1%8d-2022-%d0%bf%d0%be-%d0%bc%d0%b0%d1%82%d0%b5%d0%bc%d0%b0%d1%82%d0%b8%d0%ba%d0%b5-%d0%bf/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
Заголовок сообщения: Re: Тренировочный вариант №372
Добавлено: 15 дек 2021, 06:12
|
Зарегистрирован: 04 дек 2021, 02:16
Сообщений: 11
hpbhpb писал(а):
Елена Р писал(а):
У меня так
Да, Вы правы. Нашла у себя выч. ошибку


rgg
Заголовок сообщения: Re: Тренировочный вариант №372
Добавлено: 15 дек 2021, 06:29
Зарегистрирован: 29 окт 2014, 22:13
Сообщений: 3763
Елена Р писал(а):
hpbhpb писал(а):
Елена Р писал(а):
У меня так
Да, Вы правы. Нашла у себя выч. ошибку
Ответ аналогичный.


Владимiръ
Заголовок сообщения: Re: Тренировочный вариант №372
Добавлено: 16 дек 2021, 00:00
Зарегистрирован: 08 мар 2017, 23:11
Сообщений: 545
Откуда: Пущино


netka
Заголовок сообщения: Re: Тренировочный вариант №372
Добавлено: 16 дек 2021, 01:02
Зарегистрирован: 20 мар 2011, 22:29
Сообщений: 2788
Откуда: Казань
Всем доброй ночи и будьте здоровы! 

Решение заданий 12 и 14.
Решение задания 17.
Очень симпатичная задача, спасибо!


netka
Заголовок сообщения: Re: Тренировочный вариант №372
Добавлено: 16 дек 2021, 01:08
Зарегистрирован: 20 мар 2011, 22:29
Сообщений: 2788
Откуда: Казань
Решение задания 13.
Вложение:
372-13.ggb [11.13 KIB]
Скачиваний: 577
скрин решения
ух ты, сегодня ни разу не выкинуло!


antonov_m_n
Заголовок сообщения: Re: Тренировочный вариант №372
Добавлено: 16 дек 2021, 01:45
|
Зарегистрирован: 12 июн 2016, 12:25
Сообщений: 2112
Откуда: Москва
Доброй ночи . Решение задачи 16 :
| Вложения: |
|
6B6EE25B-2B3A-47E5-A808-D3C7BFB7C080_1_201_a.jpeg [ 456.06 KIB | Просмотров: 2892 ]
|
_________________
Чтобы добраться до источника, надо плыть против течения.


Kirill Kolokolcev
Заголовок сообщения: Re: Тренировочный вариант №372
Добавлено: 16 дек 2021, 01:53
Зарегистрирован: 08 май 2015, 03:53
Сообщений: 1610
Откуда: Москва
Всем доброй ночи!
решение 18
| Вложения: |
|
372_18.pdf [109.33 KIB] Скачиваний: 2182
|


rgg
Заголовок сообщения: Re: Тренировочный вариант №372
Добавлено: 16 дек 2021, 04:11
Зарегистрирован: 29 окт 2014, 22:13
Сообщений: 3763
Выкладываю подробное решение задачи 12.
Поправка: в тексте решения в соответствующих местах просьба восстановить пропущенные при печатании знаки «-» (минус) перед цифрами 2. (2sin3x*cos3x=—2″ и sin6x=—2″.
| Вложения: |
|
12_372.pdf [323.68 KIB] Скачиваний: 2109
|
Последний раз редактировалось rgg 16 дек 2021, 04:33, всего редактировалось 2 раз(а).


rgg
Заголовок сообщения: Re: Тренировочный вариант №372
Добавлено: 16 дек 2021, 04:15
Зарегистрирован: 29 окт 2014, 22:13
Сообщений: 3763
Решение задачи 13 двумя методами: координатно-векторным и геометрическим.


rgg
Заголовок сообщения: Re: Тренировочный вариант №372
Добавлено: 16 дек 2021, 04:21
Зарегистрирован: 29 окт 2014, 22:13
Сообщений: 3763
Выкладываю подробное решение задачи 14.


Канал видеоролика: Математикс
Смотреть видео:
#математикаогэ #гвэ #егэответы #числа #математика #алгебра #учиться #e_math #егэматематика
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:
Разбор Задачи №19 из Варианта Ларина №276
Математикс

Разбор Задачи №13 из Варианта Ларина №277
Математикс

Разбор Задачи №15 из Варианта Ларина №277
Математикс

Разбор Задачи №18 из Варианта Ларина №277
Математикс
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
12.12.2021
- Комментарии
RSS
Написать комментарий
Нет комментариев. Ваш будет первым!
Ваше имя:
Загрузка…
Решаем ЕГЭ 264 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №264 (alexlarin.com)
Решаем ЕГЭ 264 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №264 (alexlarin.com)
Задание 1
Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 12500 рублей. Какую сумму он получит после вычета налога на доходы? Ответ дайте в рублях.
Ответ: 10875
Скрыть
После вычета он получит 100-13=87% от своей зарплаты , т.е : 12500*0,87=10875 рублей.
Задание 2
На диаграмме показан средний балл участников 10 стран в тестировании учащихся 8‐го класса по математике в 2007 году (по 1000‐бальной шкале). Найдите средний балл участников страны, занимающей третье место в данном списке.
Ответ: 495
Скрыть
Третье место занимает Австралия и ее средний бал 495
Задание 3
Из фанерного листа размером 60 см х 60 см нужно выпилить закрашенный многоугольник. Найдите его массу (в граммах), если известно, что плотность данной фанеры равна 0,5 г/см2.
Ответ: 575
Скрыть
Найдем площадь данной фигуры: $$S=60*60-frac{1}{2} (60*50+60*10+40*10)-frac{40+50}{2}*10=$$$$3600-2000-450=1150$$ см2
Найдем его массу: $$m=1150*0,5=575$$ грамм
Задание 4
На тренировке баскетболист Майкл попадает 3‐очковый бросок с вероятностью 0,9, если бросает мячом фирмы «Nike». Если Майкл выполняет 3‐очковый бросок мячом фирмы «Adidas», то попадает с вероятностью 0,7. В корзине лежат 10 тренировочных мячей: 6 фирмы «Nike» и 4 фирмы «Adidas». Майкл наудачу берет из корзины первый попавшийся мяч и совершает 3‐очковый бросок. Найдите вероятность того, что бросок Майкла будет точен.
Ответ: 0,82
Скрыть
Вероятность выбрать Nike и попасть им: $$P_{1}=frac{6}{6+4}*0,9=0,54$$; выбрать Adidas и попасть им: $$P_{2}=frac{4}{6+4}*0,7=0,28$$. Тогда вероятность вообще попасть: $$P=0,54+0,28=0,82$$
Задание 5
Найдите корень уравнения $$frac{2}{log_{2} (-5x-1)}=-1$$
Ответ: -0,25
Скрыть
$$frac{2}{log_{2}(-5x-1)}=-1Leftrightarrow$$ $$left{begin{matrix}-5x-1>0log_{2}(-5x-1)neq 0-log_{2}(-5x-1)=2(1)end{matrix}right.$$
(1): $$log_{2}(-5x-1)=-2Leftrightarrow$$ $$-5x-1=2^{-2}Leftrightarrow$$ $$-5x=frac{1}{4} +1Leftrightarrow$$ $$-5x=frac{5}{4} Leftrightarrow$$ $$x=-0,25$$.
Задание 6
В треугольнике АВС проведена биссектриса ВК. Определите длину отрезка АК, если известно, что АВ=7,5, ВС=6, СК=4.
Ответ: 5
Скрыть
По свойству биссектрисы: $$frac{BC}{AB}=frac{KC}{AK}Leftrightarrow$$ $$AK=frac{AB*KC}{BC}=frac{7,5*4}{6}=5$$
Задание 7
Движение автомобиля во время торможения описывается формулой $$S(t)=36t-5t^{2}$$ , где S – путь в метрах, t – время в секундах. Сколько секунд автомобиль будет двигаться с момента начала торможения до его полной остановки?
Ответ: 3,6
Скрыть
Производная функции расстояния есть функция скорости, найдем ее и приравняем к 0: $${S}'(t)=v(t)=36-10tRightarrow$$ $$v(t)=0$$ или $$t=3,6$$
Задание 8
В прямоугольном параллелепипеде ABCDA1В1C1D1 , АВ=5, AD=3, AA1=4. Найдите тангенс угла между прямыми BD1 и DC.
Ответ: 1
Скрыть
1) $$ADperp AB$$ ; $$DD_{1}perp (ABC)Rightarrow$$ $$D_{1}Aperp AB$$ по теореме о трех перпендикулярах; $$ABleft | right |DC$$. Тогда $$tg (BD_{1}; DC)=tg(BD_{1}, AB)=frac{AD_{1}}{AB}$$
2) из $$Delta AD_{1}D$$: $$AD_{1}=sqrt{AD^{2}+AD_{1}^{2}}=5$$
3) $$tg (BD_{1}; AB)=frac{5}{5}=1$$
Задание 9
Найдите значение выражения $$log_{2} ^{3} (log_{3} sqrt[4]{3})$$
Ответ: -8
Скрыть
$$log_{2}^{3}(log_{3}sqrt[4]{3})=$$$$log_{2}^{3}log_{3}3^{frac{1}{4}}=$$$$log_{2}^{3}frac{1}{4}=$$$$log_{2}^{3}2^{-2}=(-2)^{3}=-8$$
Задание 10
Деталью некоторого прибора является вращающаяся катушка. Она состоит из трёх однородных соосных цилиндров: центрального массой m=8 кг и радиуса R=5 см, и двух боковых с массами M=2 кг и с радиусами R+h. При этом момент инерции катушки относительно оси вращения, выражаемый в кг*см2 , задаётся формулой $$I=frac{(m+2M)R^{2}}{2}+M(2Rh+h^{2})$$ . При каком максимальном значении h момент инерции катушки не превышает предельного значения 1900 кг*см2? Ответ выразите в сантиметрах.
Ответ: 25
Скрыть
Подставим имеющееся значение : $$1900=frac{(8+2*2)*5^{2}}{2}+2*(2*5*h+h^{2})Leftrightarrow$$ $$3800=300+40h+4h^{2}Leftrightarrow$$ $$4h^{2}+40h-3500=0Leftrightarrow$$ $$h^{2}+10h-875=0$$
$$D=100+3500=3600Leftrightarrow$$ $$h_{1}=frac{-10+60}{2}=25$$; $$h_{2}=frac{-10-60}{2}=-35$$
Тогда $$h_{max}=25$$, так как не может быть отрицательной
Задание 11
Три числа составляют арифметическую прогрессию. Если первые два оставить, а к третьему прибавить сумму двух первых, то полученные числа составят геометрическую прогрессию. Найдите знаменатель геометрической прогрессии.
Ответ: 3
Скрыть
Пусть первое число – x, третье — y, тогда по свойству арифметической прогрессии, второе: $$frac{x+y}{2}$$
Прибавим к третьему сумму первых двух, тогда она составит : $$y+x+frac{x+y}{2}=frac{3(x+y)}{2}$$
Знаменатель геометрической прогрессии- отношение последующего члена к предыдущему (третьего ко второму) : $$q=frac{3(x+y)}{2} frac{x+y}{2}=3$$
Задание 12
Найдите точку минимума функции $$f(x)=2sqrt[3]{x^{2}}-frac{sqrt[3]{x^{4}}}{4}$$
Ответ: 0
Скрыть
Найдем производную для данной функции : $${y}’=(2*sqrt[3]{x^{2}}-frac{sqrt[3]{x^{4}}}{4})=$$$$2{(x^{frac{2}{3}})}’-frac{1}{4}{(x^{frac{4}{3}})}’=$$$$2*frac{2}{3}*x^{-frac{1}{3}}-frac{1}{4}*frac{4}{3}x^{frac{1}{3}}=0Leftrightarrow$$$$frac{4}{3} *frac{1}{sqrt[3]{x}}-frac{1}{3}*sqrt[3]{x}=0Leftrightarrow$$ $$frac{1}{3}(frac{4}{sqrt[3]{x}}-sqrt[3]{x})=0Leftrightarrow$$ $$frac{4-sqrt[3]{x^{2}}}{sqrt[3]{x}}=0Leftrightarrow$$ $$sqrt[3]{x^{2}}=4Leftrightarrow$$ $$x^{2}=64Leftrightarrow$$ $$x=pm 8$$ Тогда $$x=0$$ –точка минимума
Задание 13
а) Решите уравнение $$2|sin x|+log_{tg x} (-frac{|cos x|}{sin x})=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{3pi}{2};0]$$
Ответ: А)$$-frac{5pi }{6} +2 pi n,n in Z$$ Б)$$-frac{5pi}{6}$$
Скрыть
А) $$2 left | sin x right |+log_{tg x}(-frac{left | cos x right |}{sin x})=0$$
ОДЗ: $$left{begin{matrix}frac{-left | cos x right |}{sin x}>0tg x>0tg x neq 1sin xneq 0cos xneq 0end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}sin x<0cos x<0 (1)tg xneq 1end{matrix}right.$$
Решение с учетом ОДЗ: $$-2 sin x+log_{tg x}frac{cos x}{sin x}=0Leftrightarrow$$ $$-log_{tg x}frac{sin x}{cos x}=2 sin xLeftrightarrow$$ $$2 sin x=-1Leftrightarrow$$ $$sin x=-frac{1}{2}Leftrightarrow$$$$left[begin{matrix}x=-frac{pi}{6}+2 pi n notin (1)x=-frac{5pi }{6} +2 pi nend{matrix}right.$$$$n in Z$$
Б) На промежутке: $$[-frac{3pi}{2};0]$$ : $$-frac{5pi}{6}$$
Задание 14
В правильной шестиугольной пирамиде SABCDEF сторона основания ABCDEF равна 2, а боковое ребро 3.
а) Докажите, что плоскость AFM , где M ‐ середина ребра SC, делит ребро SB в отношении 2:1, считая от вершины S.
б) Найдите площадь сечения пирамиды SABCDEF плоскостью AFM .
Ответ: А)2:1 Б) $$frac{13sqrt{2}}{3}$$
Скрыть
A) 1) Соединим AM , через M проведем прямую $$aleft | right |AF$$; $$acap SD=NRightarrow$$ $$MNleft | right |AF$$
2) AC-проекция AM ; Пусть SR-высота в $$Delta ASC$$; $$SRcap AM =K Rightarrow$$ через K пойдет прямая , параллельная AF ( по ней пересекаются сечение и (SEB) ); пусть она пересекает SE и SB в H и G соответственно , тогда (AGMNF)-искомое сечение
3) из $$Delta AMC$$ и точки $$S in GM$$ по т. Менелая : $$frac{SK}{KR}=frac{RA}{AC}*frac{CM}{MS}=1$$; $$Delta SAC$$ равнобедренный $$Rightarrow$$ $$AR=RCRightarrow$$ $$frac{SK}{KR}*frac{1}{2}*frac{1}{1}=1Rightarrow$$ $$frac{SC}{KR}=frac{2}{1}(*)$$ ( можно сразу сказать , что K-точка пересечения медиан $$Rightarrow$$ 2: 1)
4) $$Delta SHGsim Delta SEBRightarrow$$ $$Delta SGKsim Delta SBKRightarrow$$ $$frac{SK}{KR}=frac{SC}{SB}=frac{2}{1}$$
Б) 1) Пусть SO-высота пирамиды $$Rightarrow$$ из $$Delta SOB$$: $$SO=sqrt{SB^{2}-OB^{2}}=sqrt{5}Rightarrow$$ $$YO=frac{1}{3} SO=frac{sqrt{5}}{3}$$;
2) из $$Delta FOA$$: $$OZ=OA*sin A=2*frac{sqrt{3}}{2}=sqrt{3}Rightarrow$$ из $$Delta ZOY$$: $$ZY=sqrt{ZO^{2}+OY^{2}}=frac{sqrt{32}}{3}Rightarrow$$ $$cos YZO=frac{ZO}{ZY}=frac{3sqrt{3}}{sqrt{32}}$$
3) Пусть $$AG^{‘}M^{‘}N^{‘}H^{‘}F$$- проекция сечения на (ABC) и $$S _{AC_{1}^{‘}M^{‘}N^{‘}H^{‘}F}=S_{1}$$. Пусть S-площадь сечения $$Rightarrow$$ $$S=frac{S_{1}}{cos YZO}$$
4) $$S_{ZOA}=x=frac{1}{2} *2*2*frac{sqrt{3}}{2}=sqrt{3}$$;
$$S_{AOC_{1}^{‘}}=S_{ZOH^{‘}}=$$$$frac{OC_{1}^{‘}}{OB}*x=$$$$frac{SC_{1}}{SB}*x=frac{2}{3}x=frac{2sqrt{3}}{3}$$
Аналогично: $$S_{G^{‘}OM^{‘}}=S_{H^{‘}ON^{‘}}=$$$$frac{2}{3}*frac{1}{2}x=frac{1}{3}x$$ и $$S_{N^{‘}OM^{‘}}=frac{1}{4}x$$
Тогда $$S_{1}=sqrt{3} (1+2*frac{2}{3}+2*frac{1}{3}+frac{1}{4})=frac{13sqrt{3}}{4}$$
$$S=frac{13sqrt{3}}{4} :frac{3sqrt{3}}{sqrt{32}}=$$$$frac{13sqrt{3}*4sqrt{2}}{4*3sqrt{3}}=$$$$frac{13sqrt{2}}{3}$$
Задание 15
Решите неравенство $$log_{frac{1}{4}} (sqrt{x+3}-x+3) geq -2+log_{frac{1}{4}} frac{3}{8}$$
Ответ: $${-3}cup [-2 ;6)$$
Скрыть
$$log_{frac{1}{4}}(sqrt{x+3}-x+3)geq -2+log_{frac{1}{4}} frac{3}{8}$$
ОДЗ: $$left{begin{matrix}x+3geq 0sqrt{x+3}-x+3>0end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}xgeq -3sqrt{x+3}>x-3 (1)end{matrix}right.$$
(1) :решим графически: $$x in [-3 ; 6]$$
Решение: $$log_{frac{1}{4}}(sqrt{x+3}-x+3)geq log_{frac{1}{4}}16+log_{frac{1}{4}}frac{3}{8}Leftrightarrow$$
$$log_{frac{1}{4}}(sqrt{x+3}-x+3)geq log_{frac{1}{4}}16*frac{3}{8}Leftrightarrow$$ $$sqrt{x+3}-x+3leq 6Leftrightarrow sqrt{x+3}leq x+3$$
Пусть $$sqrt{x+3}=ygeq 0Leftrightarrow$$ $$x+3=y^{2}$$:$$left{begin{matrix}yleq y^{2}ygeq 0end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}y^{2}-ygeq 0ygeq 0end{matrix}right.Leftrightarrow$$$$left{begin{matrix}(y-1)ygeq 0ygeq 0end{matrix}right.Leftrightarrow$$ $$left[begin{matrix}ygeq 0left{begin{matrix}yleq 0ygeq 0end{matrix}right.end{matrix}right. Leftrightarrow$$ $$left{begin{matrix}y=0ygeq 1end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}sqrt{x+3}=0sqrt{x+3}geq 1end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}x=-3xgeq -2end{matrix}right.$$
С учетом ОДЗ : $$x in$$ $${-3}cup [-2 ;6)$$
Задание 16
В треугольнике АВС длина АВ равна 3, $$angle ACB=arcsin frac{3}{5}$$ , хорда KN окружности, описанной около треугольника АВС, пересекает отрезки АС и ВC в точках M и L соответственно. Известно, что $$angle ABC=angle CML$$ , площадь четырехугольника ABLM равна 2, а длина LM равна 1.
А) Найдите высоту треугольника KNC, опущенную из вершины С
Б) Найдите площадь треугольника KNC
Ответ: А)$$frac{1}{2}$$ Б)$$frac{3}{4}$$
Скрыть
A) $$angle C$$ – общий ; $$angle ABC =angle CMLRightarrow$$ $$Delta ABCsim Delta CML$$: $$frac{MC}{BC}=frac{CN}{AC}=frac{MN}{AB}=frac{1}{3}Rightarrow$$ $$S_{MCN}=(frac{1}{3})^{2} S_{ABC}Rightarrow$$ $$S_{AMNB}=frac{8}{9}S_{ABC}Rightarrow$$ $$S_{ABC}=frac{9 S_{AMNB}}{8}=frac{9}{4}$$$$Rightarrow$$ $$S_{MCN}=frac{1}{4}=frac{1}{2} MN*h$$ ,где h-высота из $$CRightarrow h=frac{1}{2}$$
Б) 1) Пусть O — центр описанной около $$Delta ABC$$ окружности , тогда $$OC=OB=OA$$ — радиусы и $$OC=frac{AB}{2 sin ACB}=frac{5}{2}$$
2) Пусть $$angle ABC=alpha Rightarrow$$ $$smile AC=2alpha$$ (вписанный угол) и $$angle LMC=alpha$$ .
3) $$angle LMC$$ — угол между хордами AC и KN $$Rightarrow$$ $$frac{smile AK+smile CN}{2}=alpha Rightarrow$$ $$smile AK+smile CN=2alpha$$. При этом $$smile AC=smile AK+smile KC=2alpha Rightarrow$$ $$smile CN=smile KCRightarrow$$ $$KC=CN$$
4) Пусть $$OCcap KN=DRightarrow$$ $$CD=h=frac{1}{2}$$( расстояние от C до ML ) $$Rightarrow$$ $$OD=OC-DC=frac{5}{2}-frac{1}{2}=2Rightarrow$$ $$KD=sqrt{OK^{2}-OD^{2}}=1,5Rightarrow$$ $$KN=3Rightarrow$$ $$S_{KCN}=frac{1}{2}*CD*KN=frac{3}{4}$$
Задание 17
На счет, который вкладчик имел в начале первого квартала, начисляется в конце этого квартала r1 процентов, а на тот счет, который вкладчик имел в конце второго квартала, начисляется в конце этого квартала r2 процентов, причем r1+r2=150 . Вкладчик положил на счет в начале первого квартала некоторую сумму и снял в конце того же квартала половину этой суммы. При каком значении r1 счет вкладчика в конце второго квартала окажется максимально возможным?
Ответ: 100
Скрыть
Пусть S-первоначальная сумма вклада, тогда после первого начисления на счете $$S(1+frac{r_{1}}{100})$$, а после снятия половины первоначального вклада: $$S(1+frac{r_{1}}{100})-frac{S}{2}$$. Учтем, что $$r_{2}=150-r_{1}$$.
После второго начисления на счету : $$(S(1+frac{r_{1}}{100})-frac{S}{2})(1+frac{150-r_{1}}{100})=S(r_{1})$$
Необходимо найти точку максимума: $$S^{‘}(r_{1})=(S(frac{1}{2}+frac{r_{1}}{100})(frac{250-r_{1}}{100}))^{‘}=$$$$(S(frac{50+r_{1}}{200})(frac{250-r_{1}}{100}))^{‘}$$
При этом максимум $$S(r_{1})$$ совпадает с максимумом $$K(r_{1})=(50+r_{1})(250-r_{1})$$
$$K^{‘}(r_{1})=(250-r_{1})-(50+r_{1})=0Leftrightarrow$$ $$200-2r_{1}=0Leftrightarrow$$ $$r_{1}=100$$
Задание 18
При каких значениях параметра a неравенство $$log_{frac{-2a-13}{5}} (frac{sin x -sqrt{3}cos x -a-4}{5})>0$$ выполняется для любых значений x ?
Ответ: $$(-infty ;-11)cup (-7;-6,5)$$
Скрыть
Пусть $$m(x) =sin x-sqrt{3}cos x$$, тогда $$m^{‘}(x)=cos x+sqrt{3}sin x=0Leftrightarrow$$ $$sqrt{3}tg x=-1Leftrightarrow$$ $$x=-frac{pi}{6}+pi n , n in Z$$
$$m(-frac{pi}{6})=sin -frac{pi}{6}-sqrt{3}cos -frac{pi}{6}=-frac{1}{2}-frac{3}{2}=-2rightarrow m_{min}$$
$$m(frac{5pi}{6})=sin frac{5 pi}{6}-sqrt{3} cos frac{5 pi}{6}=2rightarrow m_{max}$$
Получим систему:
$$left{begin{matrix}(frac{-2a-13}{5}-1)(frac{m-a-4}{5}-1)>0(4)frac{-2a-13}{5}>0(1)frac{m-a-4}{5}>0(3)frac{-2a-13}{5}neq 1(2)end{matrix}right.$$
$$ (1): -2a-13>0Leftrightarrow a<-6,5$$
$$(2): -2a-13neq 5Leftrightarrow aneq -9$$
$$(3) :a<-6,5 , -a-4>2,5 Rightarrow frac{m-a-4}{5}>0$$ при любом m( и ,следовательно, x)
$$(4) :(-2a-18)(m-a-9)>0Leftrightarrow$$ $$left[begin{matrix}left{begin{matrix}-2a-18>0m-a-9>0end{matrix}right. left{begin{matrix}-2a-18<0m-a-9<0end{matrix}right.end{matrix}right.Leftrightarrow$$ $$left[begin{matrix}left{begin{matrix}x<-9m-a-9>0end{matrix}right. (5)left{begin{matrix}x>-9m-a-9<0end{matrix}right.(6)end{matrix}right.$$
$$(5)$$: при $$a<-9$$: $$-a-9>0$$ при любом a , следовательно, чтобы было решение для любого m должно выполняться: $$m_{min}-a-9>0Leftrightarrow$$ $$-2-a-9>0Leftrightarrow$$ $$a<-11$$. Получим $$a in (-infty ;-11)$$
$$(6)$$ : аналогично $$m_{max}-a-9<0Rightarrow$$ $$2-a-9<0Rightarrow a>-7$$. Получим $$a in (-7; +infty )$$
С учетом (1): $$a in (-infty ;-11)cup (-7;-6,5)$$
Задание 19
Задано число от 1 до n. За один ход можно выбрать произвольное подмножество множества чисел от 1 до n и спросить, принадлежит ли ему заданное число. При ответе «да» будет начислено a баллов, при ответе «нет» – b баллов.
а) Можно ли наверняка угадать число, получив не менее 16 и не более 21 баллов, если $$a=3, b=1, n=128$$
б) Может ли n быть равным 144, если известно, что число можно наверняка угадать, получив не менее 11 баллов, и при этом $$a=2, 1leq bleq 4$$ ?
в) Какую наименьшую сумму баллов можно получить, чтобы наверняка угадать число, если $$a=3,b=1, 128leq nleq 170$$ ?
Ответ: а) да; б) нет; в) 8
Сайт заблокирован за не оплату услуг хостинга или нарушения правил.
Бесплатный конструктор сайтов
Создайте сайт без технических знаний!
Большой выбор готовых шаблонов для создания сайта
Подробнее
Хостинг сайтов SSD от 55 рублей
У нас можно купить хостинг и получить бесплатно домен и SSL сертификат
Бесплатное тестирование хостинга
Подробнее
Регистрация доменов от 99 рублей
Мы гарантируем самые низкие цены на регистрацию доменов в популярных зонах
Подробнее
SSL сертификаты для сата от 399 рублей
Купите SSL сертификат для сайта и получите месяц хостинга бесплатно
Подробнее
VPS сервера от 209 рублей
Виртуальные серверы VPS с быстрой активацией услуг
Подробнее
Выделенный сервера от 3499 рублей
Огромный выбор выделенных серверов по всему миру
Подробнее
ПОДЕЛИТЬСЯ
Тренировочный вариант №374 Алекса Ларина ЕГЭ 2022 по математике профильный уровень 11 класс с ответами и решением по новой демоверсии ЕГЭ 2022 года для подготовки к экзамену, дата выхода варианта: 25.12.2021 (25 декабря 2021 года)
Скачать вариант Ларина
Ответы для варианта
Решать вариант Алекса Ларина №374 ЕГЭ 2022 по математике:
2)Агрофирма закупает картофель в двух хозяйствах, 60% картофеля из первого хозяйства — картофель высшего сорта, из второго хозяйства поступает 65 % картофеля высшего сорта. Всего агрофирма закупает 62 % картофеля высшего сорта. Найдите вероятность того, что картофель, купленный у этой агрофирмы, окажется из первого хозяйства.
Ответ: 0,6
3)Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.
Ответ: 48
5)Найдите объём призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые рёбра равны 32 и наклонены к плоскости основания под углом 30°.
Ответ: 18
8)Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 14 км. Путь из А в В занял у туриста 4 часа, из которых 2 часа ушло на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 1 км/ч. Ответ дайте в км/ч.
Ответ: 4
10)Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 9. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых.
Ответ: 0,17
13)На ребрах CD и BB1 куба ABCDA1B1C1D1 с ребром 12 отмечены точки Р и Q соответственно, причем DP=4, а B1Q=3. Плоскость APQ пересекает ребро СС1 в точке М. А) Докажите, что точка М является серединой ребра СС1 Б) Найдите расстояние от точки С до плоскости АPQ
15)15 декабря 2021 года Антон планирует взять кредит в размере 700 тысяч рублей на покупку машины. Условия его возврата, таковы: ‐ 1‐го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; ‐ с 10 числа по 14 число каждого месяца, необходимо выплатить одним платежом часть долга; На какое минимальное количество месяцев Антон может взять кредит, чтобы каждая выплата не превышала 90 тысяч рублей?
Ответ: 9
16)Сторона АВ квадрата ABCD равна 1 и является хордой некоторой окружности, причем остальные стороны квадрата лежат вне этой окружности. Длина касательной СК, проведенной из вершины С к этой окружности, равна 2. А) Докажите, что длина отрезка, соединяющего центр квадрата и центр окружности равна длине отрезка СК Б) Найдите диаметр окружности.
Смотрите также другие варианты Ларина ЕГЭ 2022 по математике:
-
Вариант Ларина №373 ЕГЭ 2022 по математике профиль с ответами
-
Вариант Ларина №372 ЕГЭ 2022 по математике профиль с ответами