Задание 1
Борис Абрамович купил автомобиль со скидкой 80% от рыночной цены и продал его, получив прибыль в размере 70%. С какой скидкой от рыночной цены (в процентах) был продан автомобиль?
Ответ: 66
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 2
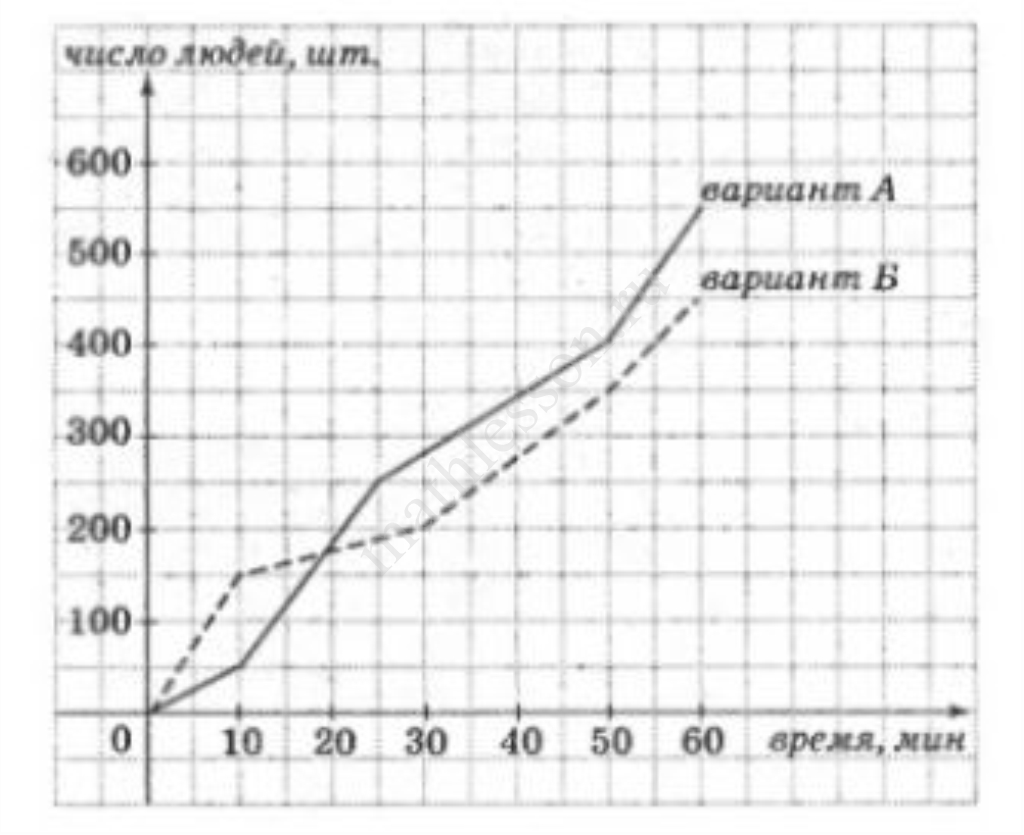
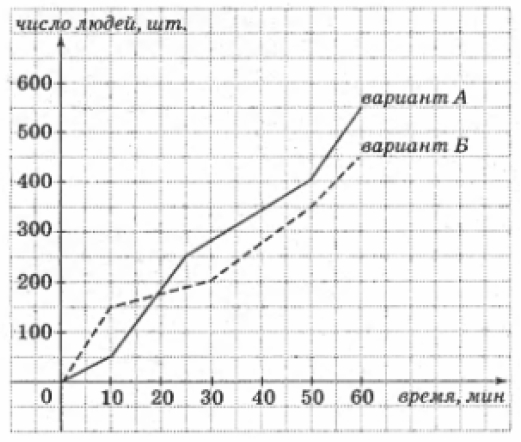
На улицах города в течение часа проводился социологический опрос, в ходе которого каждый из опрашиваемых должен был выбрать один из вариантов ответа: вариант А или вариант Б. На графиках показаны результаты этого опроса. (По горизонтальной оси откладывается время, прошедшее с начала опроса – в минутах, а по вертикальной – количество людей, выбравших за это время соответствующий вариант ответа). Какая часть людей от общего числа всех опрошенных проголосовала за последние 10 минут проведения этого опроса?
Ответ: 0,25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 3
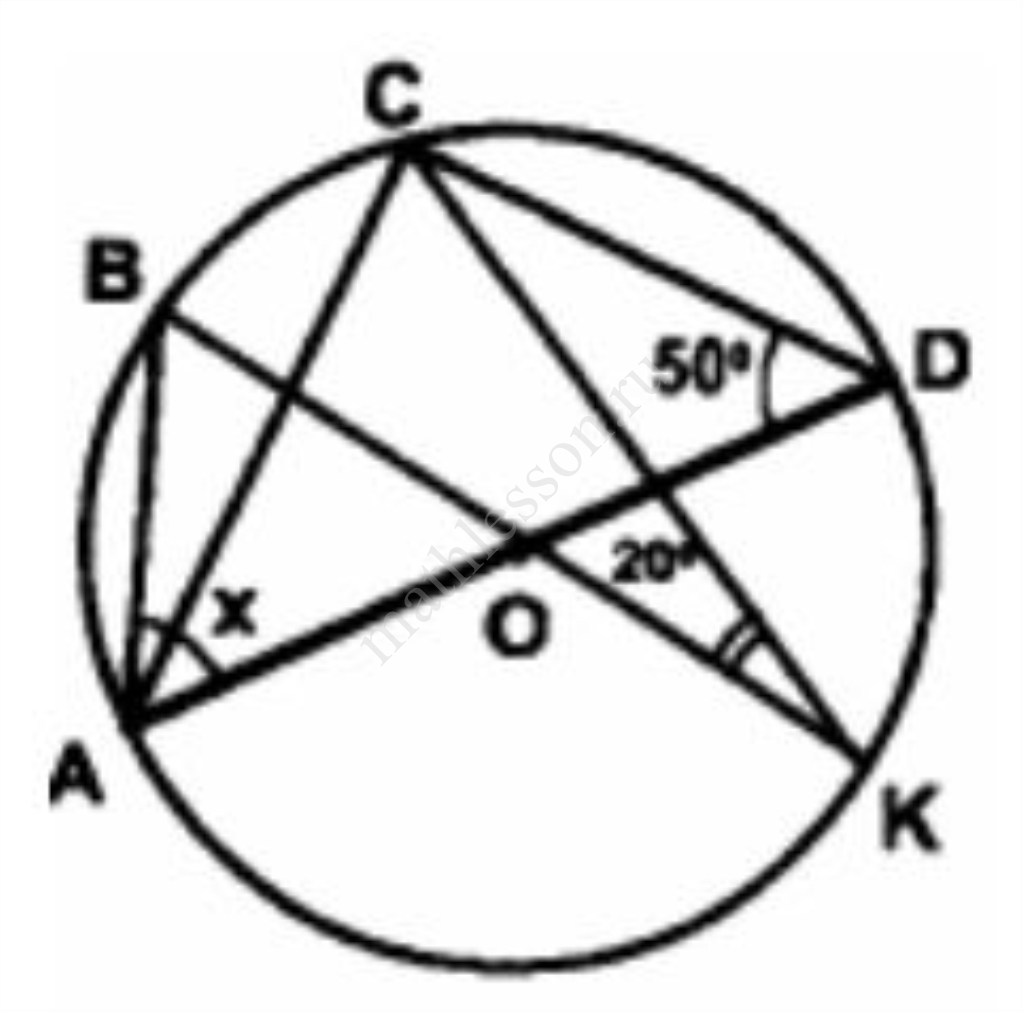
Найдите градусную меру угла BAD, изображенного на рисунке
Ответ: 60
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 4
Аня загадывает два случайных числа от 1 до 9. Найдите вероятность того, что сумма этих чисел делится на 3. Ответ округлите до сотых.
Ответ: 0,33
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 5
Найдите корень уравнения или среднее арифметическое его корней, если их несколько $$log_3 (3^{x}-3sqrt{3})+log_3 (3^{x}+3sqrt{3})=log_3(6cdot 3^{x})$$
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 6
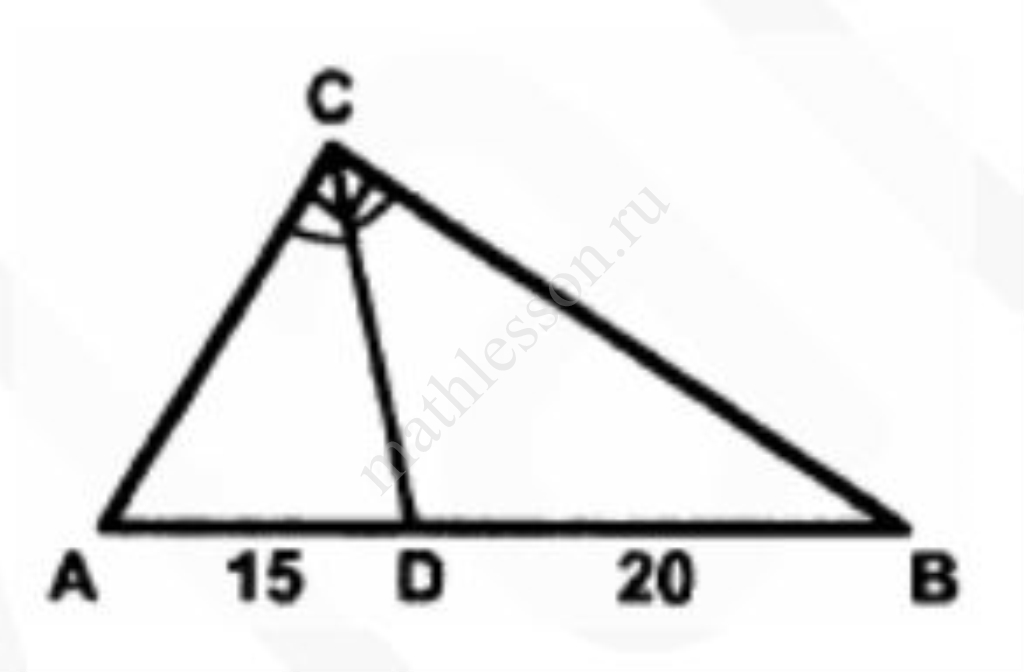
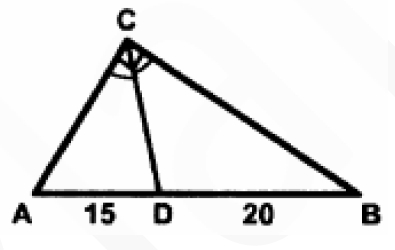
Найдите площадь прямоугольного треугольника АВС, изображенного на рисунке. CD – биссектриса угла АСВ
Ответ: 294
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 7
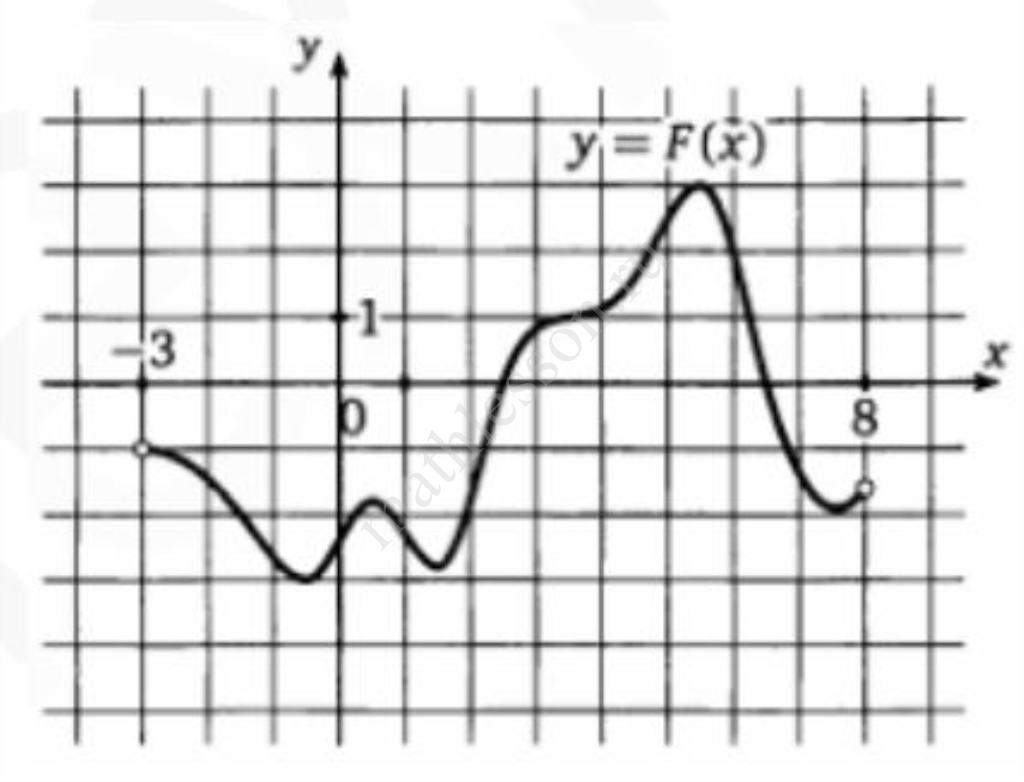
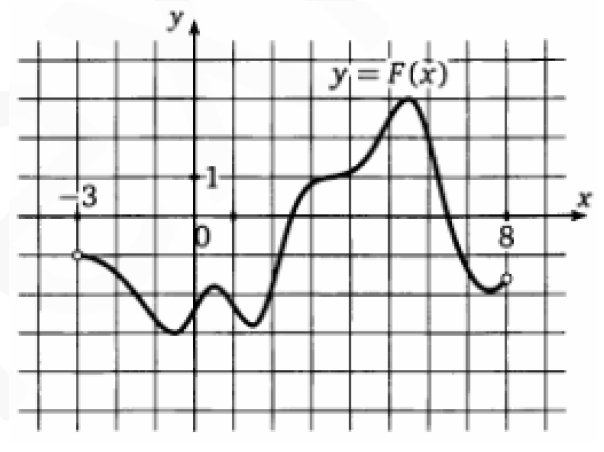
На рисунке изображен график функции $$y=F(x)$$ одной из первообразных некоторой функции $$f$$, определенной на интервале $$(-3;8)$$. Определите количество целых чисел $$x_{i}$$, для которых $$f(x_{i})$$ отрицательно.
Ответ: 5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 8
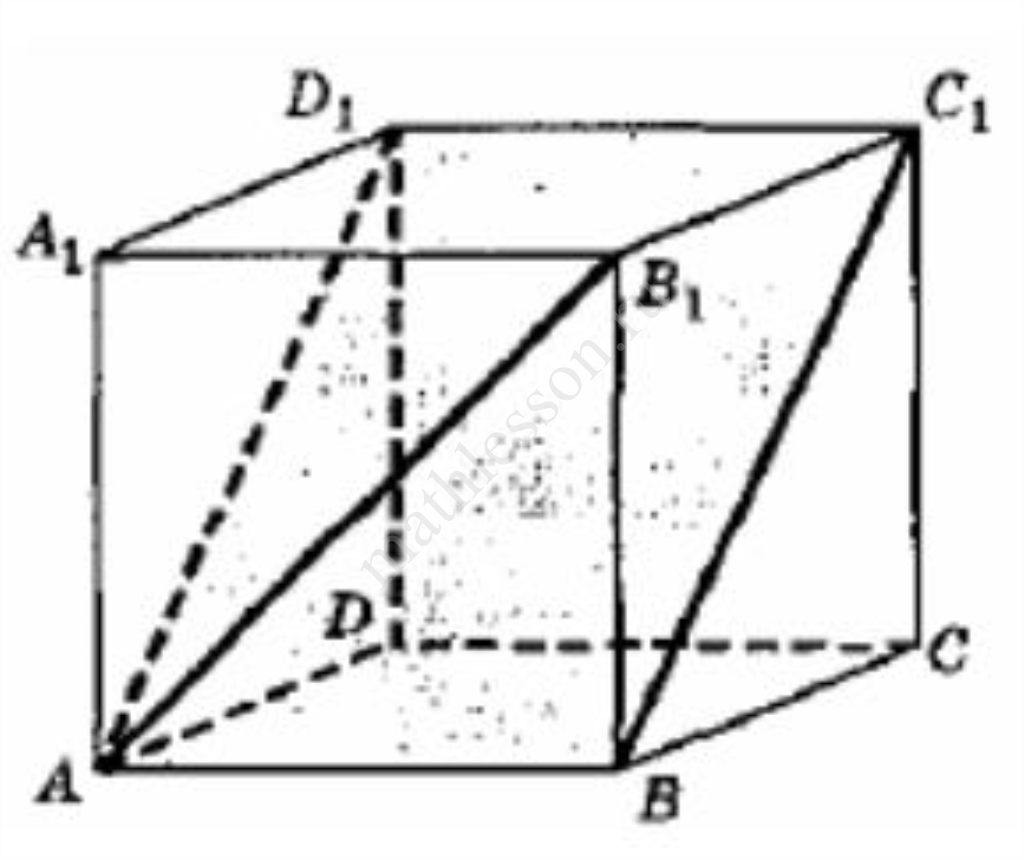
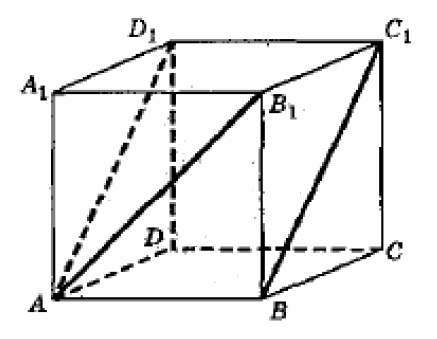
В кубе $$ABCDA_{1}B_{1}C_{1}D_{1}$$ найдите угол между прямой $$АВ$$ и плоскостью $$АВС_{1}$$. Ответ дайте в градусах.
Ответ: 30
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 9
Найдите значение выражения при $$x=14^{circ}$$: $$log_{2}(1+tg^2 x)+log_{2}(1+ctg^{2}x)+2log_{2}(sin 2x)$$
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 10
Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объем и давление связаны соотношением $$pV^{1,4}=const$$, где $$p$$ ‐ давление газа (в атмосферах), $$V$$ ‐ объем газа (в литрах). Изначально объем газа равен 294,4 л, а давление газа равно одной атмосфере. До какого объема надо сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах.
Ответ: 9,2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 11
Часы со стрелками показывают 3 часа 50 минут. Через сколько минут минутная стрелка в восьмой раз поравняется с часовой?
Ответ: 490
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 12
Найдите значение функции $$f(x)=4^{log_{4}frac{(x+3)^2}{x^{3}+12x}+log_{0,5}(x+3)}$$ в точке минимума
Ответ: 0,0625
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 13
а) Решите уравнение: $$log_{2}sin 2x+log_{1/2}cos x=frac{1}{2}$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{5pi}{2};-frac{pi}{2}]$$
Ответ: а)$$frac{pi}{4}+2pi n, nin Z$$ б)$$-frac{7pi}{4}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 14
В правильной треугольной пирамиде SABC сторона основания АВ равна 6, а боковое ребро SA равно 4. Точки М и N – середины ребер SA и SB соответственно. Плоскость $$alpha$$ содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость $$alpha$$ делит медиану СЕ основания в отношении 5:1, считая от точки С.
б) Найдите периметр многоугольника, являющегося сечением пирамиды SABC плоскостью $$alpha$$.
Ответ: $$8+2sqrt{2}$$
Задание 15
Решите неравенство: $$32cdot 2^{x^{2}+3x}-frac{2^{x^{2}+3x}}{16}+1geq 2^{3x+9}$$
Ответ: $$[-3;-2];[2;+infty)$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 16
Точки А и В лежат на окружности с центром О и радиусом 6, а точка С равноудалена от точек А, В и О. Другая окружность с центром Q и радиусом 8 описана около треугольника АСО.
а) Докажите, что точка пересечения прямых АВ и СQ лежит на окружности, описанной около треугольника ОСВ.
б) Найдите длину отрезка QB.
Ответ: 10
Задание 17
15 декабря планируется взять кредит в банке на 61 месяц. Условия его возврата таковы:
– 1‐го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
– со 2‐го по 14 число каждого месяца необходимо выплатить часть долга;
– 15‐го числа первого месяца долг должен уменьшиться на 900 тысяч рублей, все следующие месяцы долг должен быть меньше долга на 15‐е число предыдущего месяца на 30 тысяч рублей. Найдите r , если переплата по кредиту составила 1152 тыс. рублей?
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 18
Найдите все значения x, при которых равенство: $$2log_{2+a^{2}}(4-sqrt{7+2x})=log_{2+a^{2}x^{2}}(4-3x)$$ выполняется при любом значении параметра a.
Ответ: 1
Задание 19
Натуральное число, являющееся полным квадратом, обладает следующим свойством: если все его цифры уменьшить на одно и то же натуральное число, то получится число, также являющееся полным квадратом.
а) Приведите пример двухзначного числа, обладающего указанным свойством
б) Найдите все двухзначные числа, обладающие указанным свойством
в) Найдите все четырехзначные числа, обладающие указанным свойством
Ответ: а) 36 б) 36 и 49 в) 3136, 4489
Решение и ответы заданий № 1–13 варианта №316 Александра Ларина. Разбор ЕГЭ 2020 по математике (профильный уровень).
Задание 1.
Борис Абрамович купил автомобиль со скидкой 80% от рыночной цены и продал его, получив прибыль в размере 70%. С какой скидкой от рыночной цены (в процентах) был продан автомобиль?
Задание 2.
На улицах города в течении часа проводился социологический опрос, в ходе которого каждый из опрашиваемых должен был выбрать один из вариантов ответа: вариант А или вариант Б. На графиках показаны результаты этого опроса. (По горизонтальной оси откладывается время, прошедшее с начала опроса – в минутах, а по вертикальной –количество людей, выбравших за это время соответствующий вариант ответа). Какая часть людей от общего числа всех опрошенных проголосовала за последние 10 минут проведения этого опроса?
Задание 5.
Найдите градусную меру угла BAD, изображенного на рисунке
Задание 4.
Аня загадывает два случайных числа от 1 до 9. Найдите вероятность того, что сумма этих чисел делится на 3. Ответ округлите до сотых.
Задание 5.
Найдите корень уравнения или среднее арифметическое его корней, если их несколько
Задание 6.
Найдите площадь прямоугольного треугольника АВС, изображенного на рисунке. CD — биссектриса угла АСВ.
Задание 7.
На рисунке изображен график функции y = F(х) одной из первообразных некоторой функции f, определенной на интервале (-3;8). Определите количество целых чисел xi для которых f (xi) отрицательно.
Задание 8.
В кубе ABCDA1B1C1D1 найдите угол между прямой АВ1 и плоскостью АВС1. Ответ дайте в градусах.
Задание 9.
Найдите значение выражения при x = 140
Задание 10.
Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объем и давление связаны соотношением pV1,4 = const, где p — давление газа (в атмосферах), V — объем газа (в литрах). Изначально объем газа равен 294,4 л, а давление газа равно одной атмосфере. До какого объема надо сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах.
Задание 11.
Часы со стрелками показывают 3 часа 50 минут. Через сколько минут минутная стрелка в восьмой раз поравняется с часовой?
Задание 12.
Найдите значение функции 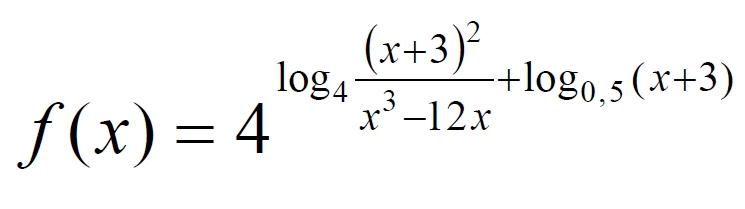
Задание 13.
а) Решите уравнение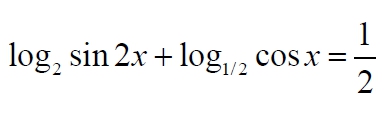
Источник варианта: alexlarin.net
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 0 / 5. Количество оценок: 0
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
А. Ларин. Тренировочный вариант № 316. (Часть C)
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 4. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5 : 1, считая от точки C.
б) Найдите периметр многоугольника, являющегося сечением пирамиды SABC плоскостью α.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Точки А и В лежат на окружности с центром О и радиусом 6, а точка С равноудалена от точек А, В и О. Другая окружность с центром Q и радиусом 8 описана около треугольника АСО.
а) Докажите, что точка пересечения прямых АВ и СQ лежит на окружности, описанной около треугольника ОСВ.
б) Найдите длину отрезка QB.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
15 декабря планируется взять кредит в банке на 61 месяц. Условия его возврата таковы:
— 1‐го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2‐го по 14 число каждого месяца необходимо выплатить часть долга;
— 15‐го числа первого месяца долг должен уменьшиться на 900 тысяч рублей, все следующие месяцы долг должен быть меньше долга на 15‐е число предыдущего месяца на 30 тысяч рублей. Найдите r, если переплата по кредиту составит 1152 тысяч рублей?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения x, при которых равенство:
выполняется при любом значении параметра a.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Натуральное число, являющееся полным квадратом, обладает следующим свойством: если все его цифры уменьшить на одно и то же натуральное число, то получится число, также являющееся полным квадратом.
а) Приведите пример двухзначного числа, обладающего указанным свойством.
б) Найдите все двухзначные числа, обладающие указанным свойством.
в) Найдите все четырехзначные числа, обладающие указанным свойством.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
| 2327 | В кубе ABCDA1B1C1D1 найдите угол между прямой AB1 и плоскостью ABC1.
Ответ дайте в градусах. |
В кубе ABCDA1B1C1D1 найдите угол между прямой AB1 и плоскостью ABC1 ! ларин егэ по математике 2020 профильный уровень Вариант 316 Задание 8 | |
| 2326 | Найдите градусную меру угла BAD, изображенного на рисунке
|
Найдите градусную меру угла BAD, изображенного на рисунке ! Тренировочный вариант 316 от Ларина Задание 3 ЕГЭ | |
| 2325 | Аня загадывает два случайных числа от 1 до 9. Найдите вероятность того, что сумма этих чисел делится на 3. Ответ округлите до сотых |
Аня загадывает два случайных числа от 1 до 9 ! Тренировочный вариант 316 от Ларина Задание 4 | |
| 2324 | Найдите корень уравнения или среднее арифметическое его корней, если их несколько log_{3}(3^x-3sqrt(3))+log_{3}(3^x+3sqrt(3))=log_{3}(6*3^x) |
Найдите корень уравнения или среднее арифметическое его корней, если их несколько log_{3}(3^x -3sqrt(3))+ log_{3}(3^x + 3sqrt(3)) = log_{3}(6* 3^x) ! Тренировочный вариант 316 от Ларина Задание 5 ЕГЭ |
|
| 2323 | Найдите площадь прямоугольного треугольника ABC, изображенного на рисунке. CD – биссектриса угла ACB
|
Найдите площадь прямоугольного треугольника ABC, изображенного на рисунке. CD – биссектриса угла ACB ! Тренировочный вариант 316 от Ларина Задание 6 ЕГЭ | |
| 2322 | Найдите значение выражения при x=14^@ log_{2}(1+tg^2x)+log_{2}(1+ctg^2x)+2log_{2}(sin 2x) |
Найдите значение выражения при x=14 градусам log_{2}(1 + tg^2x) + log_{2}(1 + ctg^2x) + 2log_{2}(sin 2x) ! ларин егэ по математике 2020 профильный уровень Вариант 316 Задание 9 | |
| 2321 | Найдите значение функции f(x)=4^(log_{4}((x+3)^2/(x^3-12x))+log_{0.5}(x+3)) в точке минимума |
Найдите значение функции f(x)= 4 ^(log_{4}( (x+ 3)^2 / (x^3 -12x)) + log_{0.5} (x +3)) в точке минимума ! Тренировочный вариант 316 от Ларина Задание 12 | |
| 2320 | а) Решите уравнение log_{2}(sin(2x))+log_{1/2}(cos(x))=1/2 б) Укажите корни этого уравнения, принадлежащие отрезку [-(5pi)/2; -pi/2]. |
а) Решите уравнение log_{2} sin 2x + log_{1/2} cos x = 1/2 ! Тренировочный вариант 316 от Ларина Задание 13 ЕГЭ |
|
| 2319 | Решите неравенство 32*2^(x^2+3x)-2^(x^2)/16+1>=2^(3x+9) |
Решите неравенство 32 * 2^(x^2 + 3x) — 2^(x^2) / 16 +1 >= 2^(3x+9) ! Тренировочный вариант 316 от Ларина Задание 15 | |
| 1729 | В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 4. Точки M и N – середины рёбер SA и SB соответственно. Плоскость alpha содержит прямую MN и перпендикулярна плоскости основания пирамиды. а) Докажите, что плоскость alpha делит медиану CE основания в отношении 5:1, считая от точки C. б) Найдите периметр многоугольника, являющегося сечением пирамиды SABC плоскостью alpha. |
В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 4 ! ларин егэ 2020 профильный уровень Вариант 316 Задание 14 # Вариант 278 Задание 14 | |
| Clear |
На чтение 1 мин Просмотров 2 Опубликовано 5 марта, 2023
Вариант №316 ЕГЭ Ларин Решение и ответы на задачи на официальном сайте источника онлайн.
Решение и ответы заданий № 1–13 варианта №316 Александра Ларина. Разбор ЕГЭ 2020 по математике (профильный уровень).
Варианты ответов и решение задачи ТУТ: https://ege314.ru/ege-varianty-larina/variant-316-ege-larin/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
Канал видеоролика: Виктор Осипов
Смотреть видео:
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:

Разбор Задания №14 из Варианта Ларина №278 ЕГЭ-2020.
Виктор Осипов

Разбор Задания №18 из Варианта Ларина №279 ЕГЭ-2020.
Виктор Осипов

Разбор Задания №16 из Варианта Ларина №278 ЕГЭ-2020
Виктор Осипов

Разбор Задания №15 из Варианта Ларина №279 ЕГЭ-2020.
Виктор Осипов
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
10.06.2020
- Комментарии
RSS
Написать комментарий
Нет комментариев. Ваш будет первым!
Ваше имя:
Загрузка…
| Автор | Сообщение | |||
|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №316
|
||||
|
http://alexlarin.net/ege/2020/trvar316.html |
|||
  |
||||
|
|
||||
|
antonov_m_n |
Заголовок сообщения: Re: Тренировочный вариант №316
|
|||
|
Здравствуйте , в 16(а) может быть точка пересечения прямых AB и CQ , а не отрезков ? 16(б) — 10 , но условие надо исправить _________________ Последний раз редактировалось antonov_m_n 06 июн 2020, 12:56, всего редактировалось 3 раз(а). |
|||
  |
||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №316
|
|||
|
Спасибо за интересный вариант! Подробности: |
|||
  |
||||
|
Math2019 |
Заголовок сообщения: Re: Тренировочный вариант №316
|
|||
|
Kirill Kolokolcev писал(а): Спасибо за интересный вариант! Подробности: Такой же ответ |
|||
  |
||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №316
|
|||
|
Очень понравилась 19. Надеюсь, нигде не ошибся в вычислениях. Подробности: |
|||
  |
||||
|
Владимир Анатольевич |
Заголовок сообщения: Re: Тренировочный вариант №316
|
|||
|
Kirill Kolokolcev писал(а): Очень понравилась 19. Надеюсь, нигде не ошибся в вычислениях. Подробности: Да! |
|||
  |
||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №316
|
|||
|
Владимир Анатольевич писал(а): Kirill Kolokolcev писал(а): Очень понравилась 19. Надеюсь, нигде не ошибся в вычислениях. Подробности: Да! Спасибо, Владимир Анатольевич! |
|||
  |
||||
|
Владимир Анатольевич |
Заголовок сообщения: Re: Тренировочный вариант №316
|
|||
|
17. Подробности: |
|||
  |
||||
|
Leonid Argail |
Заголовок сообщения: Re: Тренировочный вариант №316
|
|||
|
13 Подробности: 14 Подробности: 15 Подробности: В остальных задачах получились ответы, опубликованные коллегами. |
|||
  |
||||
|
LuckyBoyR |
Заголовок сообщения: Re: Тренировочный вариант №316
|
|||
|
Подскажите как 15 решать) |
|||
  |
||||
| Показать сообщения за: Сортировать по: |
Кто сейчас на форуме
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
|
Вы не можете начинать темы |
|
|






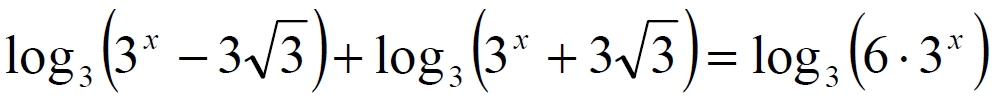
![[-5pi/2;-pi/2] Укажите корни этого уравнения, принадлежащие отрезку [-5pi/2;-pi/2]](https://ege314.ru/wp-content/uploads/2020/06/09-06-2020-11-40-23.jpg)


