Задание 1
Поезд Новосибирск‐Красноярск отправляется в 15:20 а прибывает в 4:20 на следующий день (время московское). Сколько часов поезд находится в пути?
Ответ: 13
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
До полуночи 8 часов 40 минут, после полуночи 4 часов 20 минут $$Rightarrow$$ в сумме 13 часов
Задание 2
На диаграмме показано распределение выплавки меди в 10 странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место по выплавке меди занимали США, десятое место — Казахстан. Какое место занимала Индонезия?
Ответ: 5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 3
На координатной плоскости изображён параллелограмм. Найдите его площадь.
Ответ: 7
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$S=3*4-2*frac{1}{2}-3*1-2*frac{1}{2}*2*1=7$$
Задание 4
Во время психологического теста психолог предлагает каждому из двух испытуемых А. и Б. выбрать одну из трех цифр: 1, 2 или 3. Считая, что все комбинации равновозможны, найдите вероятность того, что А. и Б. выбрали разные цифры. Результат округлите до сотых
Ответ: 0,67
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Всего возможных комбинаций: 9 — (11;12;13;21;22;23;31;32;33) Разные цифры в 6 комбинациях $$P=frac{6}{9}=0,(6)approx 0,67$$
Задание 5
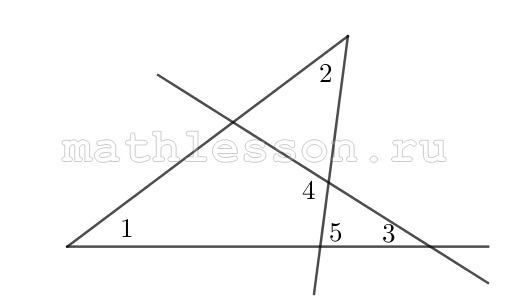
На рисунке угол 1 равен 46, угол 2 равен 30, угол 3 равен 44. Найдите угол 4. Ответ дайте в градусах.
Ответ: 120
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$angle 5=angle 1+angle 2=76$$
$$angle 4=angle 5+angle 3=76+44=120$$
Задание 6
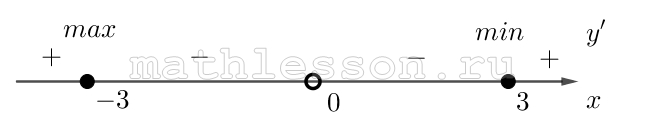
На рисунке изображен график функции f(x). Касательная к этому графику, проведенная в точке с абсциссой −4, проходит через начало координат. Найдите f'(-4).
Ответ: 0,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$Delta ABC$$: $${f}'(-4)=tgA=frac{BC}{AC}=frac{2}{4}=0,5$$
Задание 7
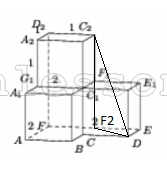
Найдите квадрат расстояния между вершинами D и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Ответ: 6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$DC^{2}_{2}=$$$$C_{2}F^{2}_{2}+DF_{2}^{2}=$$$$C_{2}F_{2}^{2}+DE^{2}+EF^{2}_{2}=$$$$2^{2}+1^{2}+1^{2}=6$$
Задание 8
Найдите значение выражения $$7cos (pi+beta)-2sin (frac{pi}{2}+beta)$$, если $$cos beta=-frac{1}{3}$$
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$7 cos (pi +B)-2sin (frac{pi}{2}+B)=$$$$-7cos beta -2cos beta =-9cosbeta =-9*(-frac{1}{3})=3$$
Задание 9
Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле $$P=frac{4mg}{pi D^{2}}$$ где m = 1200 кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая ускорение свободного падения g = 10 м/с2 , а $$pi=3$$, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400000 Па. Ответ выразите в метрах
Ответ: 0,2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Выразим D из формулы : $$P=frac{4mg}{pi D^{2}}Leftrightarrow$$ P pi D^{2}=4mgLeftrightarrow$$ $$D=sqrt{frac{4mg}{p pi}}(D>0)$$
$$D=sqrt{frac{4*1200*10}{400*3}}=$$$$sqrt{frac{4}{100}}=frac{2}{10}=0,2$$
Задание 10
Игорь и Паша могут покрасить забор за 9 часов. Паша и Володя могут покрасить этот же забор за 12 часов, а Володя и Игорь — за 18 часов. За сколько часов мальчики покрасят забор, работая втроём?
Ответ: 8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть x — производительность Игоря, y — Паши, z — Володи(в частях забора в час) . Весь забор примем за 1.
$$left{begin{matrix}frac{1}{x+y}=9\frac{1}{y+z}=12\frac{1}{x+z}=18end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}x+y=frac{1}{9}\y+z=frac{1}{12}\x+z=frac{1}{18}end{matrix}right.$$
Сложим уравнения:
$$2(x+y+z)=frac{1}{9}+frac{1}{12}+frac{1}{18}=frac{9}{36}=frac{1}{4}Leftrightarrow$$ $$x+y+z=frac{1}{8}Leftrightarrow$$ $$frac{1}{x+y+z}=8$$ часов
Задание 11
Найдите наибольшее значение функции $$y=frac{x^{3}+x^{2}+9}{x}-x^{2}$$ на отрезке [-9;-1]
Ответ: -6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$y=frac{x^{3}+x^{2}+9}{x}-x^{2}=frac{x^{3}+x^{2}+9-x^{3}}{x}=frac{x^{2}+9}{x}$$
$${y}’=frac{{(x^{2}+9)}’x-(x^{2}+9)*{x}’}{x^{2}}=frac{2x^{2}-x^{2}-9}{x^{2}}=frac{x^{2}-9}{x^{2}}=0$$
$$left{begin{matrix}x^{2}-9=0\x^{2}neq 0end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}x=pm 3\xneq 0end{matrix}right.$$
$$f(-3)=frac{(-3)^{2}+9}{(-3)}=-6$$
Задание 12
а) Решите уравнение $$sqrt{10}cos x-sqrt{4cos x-cos 2x}=0$$
б) Укажите корни этого уравнения, принадлежащие промежутку $$(-frac{pi}{3};2pi]$$
Ответ: A) $$pm frac{pi}{3}+2 pi n , n in Z$$ Б) $$frac{pi}{3};frac{5pi}{3}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
A) $$sqrt{10}cos x-sqrt{4 cos x- cos 2x}=0Leftrightarrow$$$$sqrt{4 cos x-cos 2x}=sqrt{10}cos x$$
Прейдем к равносильной системе:$$left{begin{matrix}sqrt{10} cos xgeq 0(2)\4 cos x- cos 2x =10 cos ^{2}x (1)end{matrix}right.$$
Рассмотрим (1): $$4 cos x-(2 cos^{2}x-1)-10 cos ^{2}x=0Leftrightarrow$$$$-12 cos ^{2}x+4 cos x+1=0Leftrightarrow$$$$12 cos ^{2}x-4 cos x-1=0$$
$$D=16+48=64=8^{2}$$
$$left[begin{matrix}cos x=frac{4+8}{24}=frac{1}{2}\cos x=frac{4-8}{24}=-frac{1}{6}end{matrix}right.Leftrightarrow$$ $$left[begin{matrix}x=pm frac{pi}{3}+2 pi n , n in Z\ varnothing (cos xgeq 0)end{matrix}right.$$
Б) На промежутке $$[-frac{pi}{3};2 pi n ]$$:
$$-frac{pi}{3}+2 pi n:n=1Rightarrow frac{5 pi}{3}$$
$$frac{pi}{3}+2 pi n:n=0Rightarrow frac{pi}{3}$$
Задание 13
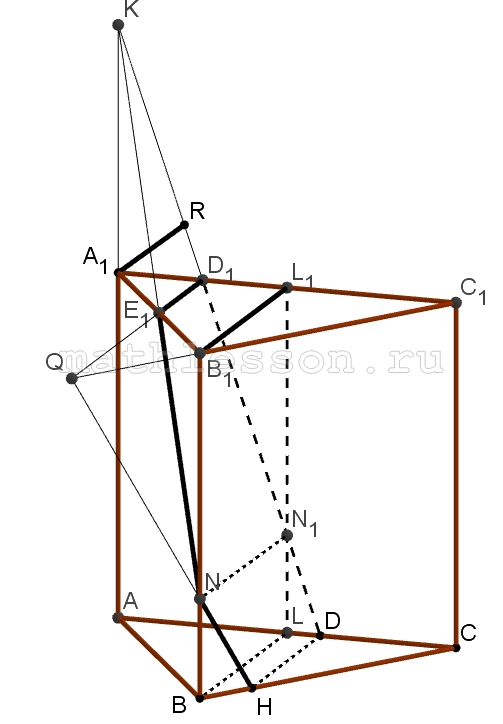
Основание прямой призмы ABCA1B1C1 равнобедренный треугольник ABC, в котором AB=BC=5, AC=6 . Высота призмы равна $$sqrt{6}$$ . На сторонах A1C1, A1B1 и AC выбраны соответственно точки D1, E1 и D так, что , $$A_{1}D_{1}=frac{A_{1}C_{1}}{4}$$, $$A_{1}E_{1}=B_{1}E_{1}$$, $$CD=frac{AC}{3}$$, и через эти точки проведена плоскость.
А) Найдите площадь сечения призмы этой плоскостью
Б) Найдите расстояние от точки A до плоскости сечения
Ответ: а) $$frac{329}{30}$$; б) $$frac{3sqrt{6}}{7}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
А) 1) Соединим $$D_{1}E_{1}$$, т.к. $$(ABC) left | right |(A_{1}B_{1}C_{1})$$, то из D пойдет прямая DH ($$DHcap BC=H$$) и $$D_{1}C_{1}left | right |DH$$
2) Пусть $$D_{1}E_{1}cap C_{1}B_{1}=Q$$. Соединим $$QHcap BB_{1}=N$$, соединим $$DD_{1}Rightarrow$$ $$D_{1}D+NE_{1}$$ — искомое сечение
3) $$A_{1}D_{1}=D_{1}L_{1}$$($$B_{1}L_{1}$$ — высота ), $$A_{1}E_{1}=E_{1}B_{1}$$$$Rightarrow$$ $$D_{1}E_{1}=frac{1}{2}B_{1}L_{1}$$ и $$D_{1}E_{1}left | right |B_{1}L_{1}$$; $$B_{1}L_{1}=sqrt{B_{1}C_{1}^{2}-L_{1}C_{1}^{2}}=4$$$$Rightarrow$$ $$E_{1}D_{1}=2$$
4) $$DHleft | right |D_{1}E_{1}Rightarrow$$ $$DHleft | right |BL$$ (BL — высота) $$Rightarrow$$ $$frac{DH}{LB}=frac{CD}{CL}$$; $$CD=frac{AC}{3}=2$$, $$CL=3Rightarrow$$ $$DH=frac{2*4}{3}=frac{8}{3}$$
5) $$S_{D_{1}N_{1}NE_{1}}=frac{D_{1}E_{1}*N_{1}N}{2}*DN_{1}$$; $$S_{NN_{1}DH}=frac{DH*NN_{1}}{2}*DN_{1}$$ ($$AA_{1}perp DH$$, $$ADperp DH$$$$Rightarrow$$ $$D_{1}Dperp DH$$); $$NK_{1}=BL=4;D_{1}B_{1}=sqrt{D_{1}L_{1}^{2}+L_{1}N_{1}^{2}}$$$ $$D_{1}L=1,5 ; LD=1$$$$Rightarrow$$ $$frac{L_{1}N_{1}}{M_{1}L}=frac{3}{2}$$ ($$Delta D_{1}L_{1}N_{1}sim Delta N_{1}LD)$$$$Rightarrow$$ $$L_{1}L=AA_{1}=sqrt{6}=5x$$$$Rightarrow$$ $$x=frac{sqrt{6}}{5}Rightarrow$$ $$L_{1}N_{1}=frac{3sqrt{6}}{5}$$, $$N_{1}L=frac{2sqrt{6}}{5}$$)
$$D_{1}B_{1}=sqrt{(frac{3}{2})^{2}+(frac{3sqrt{6}}{5})^{2}}=frac{21}{10}$$
$$D{1}D=frac{7}{2}$$
$$DN_{1}=sqrt{1^{2}+(frac{2sqrt{6}}{5})^{2}}=frac{7}{5}$$
$$S_{D_{1}N_{1}NE_{1}}=frac{2+4}{2}*frac{21}{10}=frac{63}{10}$$
$$S=frac{63}{10}+frac{14}{3}=frac{329}{30}$$
$$S_{DHN_{1}N}=frac{frac{8}{3}+4}{2}*frac{7}{5}=frac{14}{3}$$
Б) 1) Пусть $$DD_{1}cap AA_{1}=K$$ $$Delta KD_{1}A_{1}sim Delta KAD$$; $$frac{A_{1}D}{AD}=frac{KD_{1}}{KD}=frac{KA_{1}}{KA}=frac{1,5}{4}=frac{3}{8}$$. Пусть $$KA_{1}=xRightarrow$$ $$KA=x+sqrt{6}Rightarrow$$ $$frac{x}{x+sqrt{6}}=frac{3}{8}Leftrightarrow$$ $$8x=3x+3sqrt{6}Leftrightarrow$$ $$x=frac{3sqrt{6}}{5}$$. Пусть $$KD_{1}=yRightarrow$$ $$KD=y+frac{7}{2}Rightarrow$$ $$frac{y}{y+frac{7}{2}}=frac{3}{8}Rightarrow$$ $$y=frac{21}{10}$$
2) Пусть $$A_{1}Rperp KD_{1}$$, но $$A_{1}D_{1}D_{1}E_{1}$$$$Rightarrow$$ $$A_{1}Rperp D_{1}E_{1}$$ и $$A_{1}Rperp KD_{1}E_{1}$$.
$$A_{1}R=frac{A_{1}K*A_{1}D_{1}}{KD_{1}}=$$$$frac{frac{3sqrt{6}}{5}*frac{3}{2}}{frac{21}{10}}=$$$$frac{9sqrt{6}*10}{5*2*21}=frac{3sqrt{6}}{7}$$
Задание 14
Решите неравенство $$(sqrt[3]{2})^{x^{2}+4x+1}-(sqrt{3+sqrt{8}}-1)^{x}leq 0$$
Ответ: $$[-2;-frac{1}{2}]$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$(sqrt[3]{2})^{x^{2}+4x+1}-(sqrt{3+sqrt{8}}-1)^{x}leq 0$$
$$sqrt{3+sqrt{8}}=sqrt{2+1+2sqrt{2}}=sqrt{(sqrt{2}+1)^{2}}=left | sqrt{2}+1 right |=sqrt{2}+1$$
$$sqrt[3]{2}^{x^{2}+4x+1}-(sqrt{2}+1-1)^{x}leq 0Leftrightarrow$$ $$2^{frac{x^{2}+4x+1}{3}}leq 2^{frac{x}{2}}Leftrightarrow$$ $$frac{x^{2}+4x+1}{3}leq frac{x}{2}|*6Leftrightarrow$$ $$2x^{2}+8x+2leq 3xLeftrightarrow$$ $$2x^{2}+5x+2leq 0$$
$$D=25-16=9$$
$$x_{1}=frac{-5+3}{4}=-0,5$$
$$x_{2}=frac{-5-3}{4}=-2$$
$$(x+0,5)(x+2)leq 0$$
$$x in [-2, -0,5]$$
Задание 15
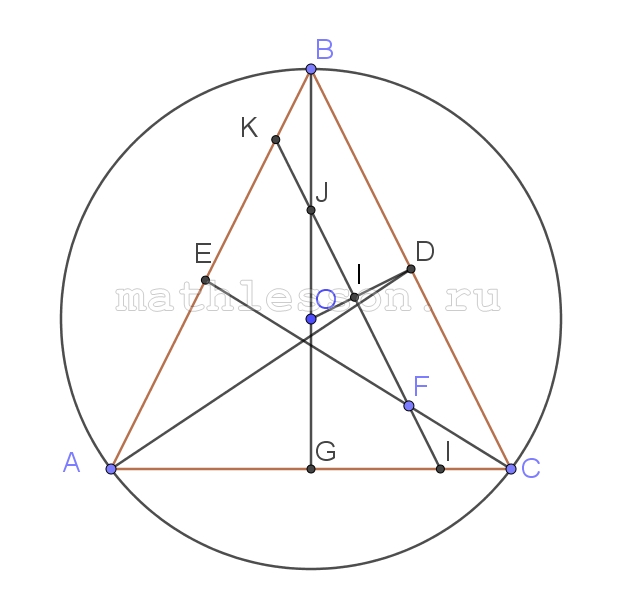
Дан треугольник АВС, в котором АВ=ВС=5, медиана $$AD=frac{sqrt{97}}{2}$$ . На биссектрисе СЕ выбрана точка F такая, что CE=5CF. Через точку F проведена прямая l, параллельная ВС.
А) Найдите расстояние от центра окружности, описанной около треугольника АВС до прямой l
Б) Найдите в каком отношении прямая l делит площадь треугольника АВС
Ответ: А) $$frac{633}{440}$$ Б)$$frac{100}{21}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
А) 1) $$Delta ABD$$: $$cos B=frac{AB^{2}+BD^{2}-AD^{2}}{2 AB*BD}=frac{7}{25}$$
2) $$Delta ABC:$$ $$AC=sqrt{AB^{2}+BC^{2}-2 AB*BC * cos B}=6$$
3) $$BG=sqrt{BC^{2}-GC^{2}}=4Rightarrow$$ $$S_{ABC}=frac{1}{2}BG*AC=12$$
4) $$BO=frac{AB*BC*AC}{4 S_{ABC}}=frac{25}{8}$$
5) $$cos BCA=frac{GC}{BC}=frac{3}{5}$$; $$angle ECG=frac{angle BCA}{2}$$$$Rightarrow$$ $$2 cos ^{2}ECG-1=frac{3}{5}$$$$Rightarrow$$ $$cos ECG=frac{2}{sqrt{5}}$$; $$sin ECG=frac{1}{sqrt{5}}$$
$$CE=frac{2 AC*CB*cos ECG}{AC+CB}=$$$$frac{120}{11sqrt{5}}$$$$Rightarrow$$ $$CF=frac{CE}{5}=frac{24}{11sqrt{5}}$$
6) Центр описанной на пересечении серединных перпендикуляров , $$BD=DCRightarrow$$ $$ODperp BC$$ и OH — расстояние
7) $$angle FIG=angle BCARightarrow$$$$sin FIG=sin BCA=frac{4}{5}$$
$$angle FIG=180-angle FIGRightarrow$$ $$sin FIC=sin FIG=frac{4}{5}$$
$$cos FIC=-cos FIG=-cos BSA=-frac{3}{5}$$
По теореме синусов: $$frac{FC}{sin FIC}=frac{FI}{sin FCI}Rightarrow$$$$FI=frac{6}{11}$$

9) $$Delta BODsim Delta BGCRightarrow$$ $$frac{OD}{GC}=frac{BO}{BC}Rightarrow$$ $$OD=frac{5}{18}$$
10) $$Delta JOHsim Delta BODRightarrow$$ $$frac{JO}{BO}=frac{OH}{OD}Rightarrow$$ $$OH=frac{633}{440}$$
Б) 1) $$Delta ABCsim Delta AKIRightarrow$$ $$S_{AKI}=S_{ABC}(frac{AI}{AC})^{2}$$
$$frac{AI}{AC}=(frac{6-frac{6}{11}}{6})^{2}=frac{100}{121}Rightarrow$$ $$S_{AKI}=frac{1200}{121}$$
2) $$S_{KBCI}=S_{ABC}-S_{AKI}=frac{252}{121}Rightarrow$$ $$frac{S_{AKI}}{S_{KBCI}}=frac{100}{21}$$
Задание 16
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
— 1‐го числа каждого месяца долг возрастает на 4 % по сравнению с концом предыдущего месяца;
— со 2‐го по 14‐е число каждого месяца необходимо выплатить часть долга;
— 15‐го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15‐е число предыдущего месяца.
Известно, что в пятый месяц кредитования нужно выплатить 44 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Ответ: 396 тыс. рублей
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть S-сумма кредита в тыс. руб. , n=9-число месяцев, r=4%. Кредит на 9 месяцев, следовательно, по основной част долга ежемесячный платеж $$frac{S}{9}$$ . Составим таблицу:
| Месяц | Долг на начало месяца | Начисленный процент | Итоговый платеж |
| 1 | S | $$frac{rS}{100}$$ | $$frac{S}{9}+frac{rS}{100}$$ |
| 2 | $$S-frac{S}{9}=frac{8S}{9}$$ | $$frac{r*8S}{100*9}$$ |
$$frac{S}{9}+frac{rS}{100}*frac{8}{9}$$ |
| 3 | $$frac{8S}{9}-frac{S}{9}=frac{7S}{9}$$ | $$frac{rS}{100}*frac{7}{9}$$ | $$frac{S}{9}+frac{rS}{100}*frac{7}{9}$$ |
| … | … | … | … |
| 5 | $$frac{6S}{9}-frac{S}{9}=frac{5S}{9}$$ | $$frac{rS}{100}*frac{5}{9}$$ | $$frac{S}{9}+frac{rS}{100}*frac{5}{9}$$ |
| … | … | … | … |
| 9 | $$frac{2S}{9}-frac{S}{9}=frac{S}{9}$$ | $$frac{rS}{100}*frac{1}{9}$$ | $$frac{S}{9}+frac{rS}{100}*frac{1}{9}$$ |
Получим $$frac{S}{9}+frac{4*S*5}{100*9}=44Leftrightarrow$$ $$5S+S=44*45Leftrightarrow$$ $$6S=44*45Leftrightarrow$$ $$S=330 $$тыс.руб.
Тогда итоговые выплаты составят: $$S+frac{rS}{100}(1+frac{8}{9}+frac{7}{9}+…+frac{1}{9})=1,2S=396$$ тыс. руб (сложили суммы с четвертого столбика)
Задание 17
При каких значениях параметра a система $$left{begin{matrix}|x-a|+|y-a|+|a+1-x|+|a+1-y|=2\ y+2|x-5|=6end{matrix}right.$$ имеет единственное решение
Ответ: $$2; frac{16}{3}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
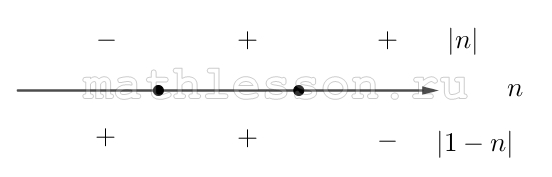
Пусть m=y-a; n=x-a, тогда имеем
$$left | m right |+left | 1-m right |=2-left | n right |-left | 1-n right |(m(n))$$
Рассмотрим раскрытие модулей:
1) $$nleq 0$$: $$2-left | n right |-left | 1-n right |=1+2n$$. Тогда $$m(n)$$: $$left | m right |+left | 1-m right |=1+2n$$. Раскроем модули:
a) $$mleq 0$$: $$-2m+1=1+2nLeftrightarrow$$ $$m=-n$$, с учетом, что $$nleq 0$$ , то $$m=-n$$ при $$n=0$$ и $$m=0$$
b) $$m in (0;1]$$: $$1=1+2nLeftrightarrow$$ $$n=0$$
c) $$m in (1;+infty )$$: $$2m-1=1+2nLeftrightarrow$$ $$m=n+1$$ при $$nleq 0$$ – решений нет
2) $$0<nleq 1$$:$$ 2-left | n right |-left | 1-n right |=1$$
a) $$mleq 0$$: $$-2m+1=1Leftrightarrow$$ $$m=0$$
b) $$0<mleq 1$$: $$1=1Rightarrow$$ решение все точки в квадрате
$$left{begin{matrix}0<nleq 1\0<mleq 1end{matrix}right.$$
c) $$m>0$$: $$2m-1=1Rightarrow$$ $$m=1$$ решений нет
3) $$n>1$$: $$2-left | m right |-left | 1-n right |=3-2n$$
a) $$mleq 0$$: $$-2m+1=3-2nLeftrightarrow$$ $$m=n-1$$, с учетом , что $$n>1$$ решений нет
b) $$a<mleq 1$$: $$1=3-2nRightarrow$$ $$n=1Rightarrow$$ решений нет
c) $$m>1$$: $$2m-1=3-2nLeftrightarrow$$ $$m=2-n$$ решений нет
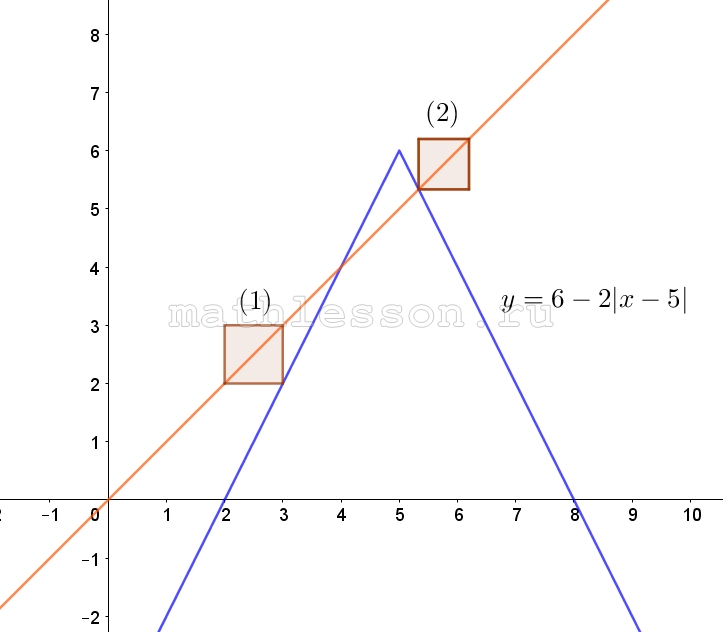
Построим график m(n). С учетом , что m=y-a и n=y-a , то график y(x) будет строиться смещение вершины (0;0) на (a;a) ( по прямой (y=x)), и построим график $$y=6-2left | x-5 right |$$ — cуществует 2 случая с одним решением :
1) При a=2
2) При пересечении вершиной и диагональю y=x части графика $$y=6-2left | x-5 right |$$(она задается y=16-2x)
$$left{begin{matrix}y=x\y=16-2xend{matrix}right.Leftrightarrow$$ $$x=16-2xLeftrightarrow$$ $$3x=16Rightarrow$$ $$x=frac{16}{3}Rightarrow$$ $$a=frac{16}{3}$$
Задание 18
В последовательности натуральных чисел a1=47 , каждый следующий член равен произведению суммы цифр предыдущего члена и a1
А) Найдите пятый член последовательности
Б) Найдите 50‐й член последовательности
В) Вычислите сумму первых пятидесяти членов этой последовательности.
Ответ: А)752 Б)940 В)34404
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
A) $$a_{2}=(4+7)*47=517$$
$$a_{3}=(5+1+7)*47=611$$
$$a_{4}=(6+1+1)*47=376$$
$$a_{5}=(3+7+6)*47=752$$
Б) вычислим еще несколько членов.
$$a_{6}=(7+5+2)*47=14*47=658$$
$$a_{7}=(6+5+8)*47=19*47=893$$
$$a_{8}=(8+9+3)*47=20*47=940$$
$$a_{9}=(9+4+0)*47=13*47=611=a_{3}$$
Получаем повторение с периодом: $$9-3=6 Rightarrow$$ $$a_{50}=a_{8}=940$$ (можно составить таблицу, можно посчитать 50-2=48(т.к. начинаем с 3-го) и 48/6=8 полных повторений без остатка , следовательно $$a_{50}$$ равен крайнему в выборке $$a_{3}…a_{8}$$)
B) $$sum_{8}^{n=3} a_{n}=61+376+752+..+940=4230$$
Тогда $$sum_{n=3}^{5a}=4230*8=33840$$
С учетом $$a_{1}$$ и $$a_{2}$$, получим $$34404$$
А. Ларин: Тренировочный вариант № 255.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
Дан треугольник ABC, в котором медиана
На биссектрисе СЕ выбрана точка F такая, что
Через точку F проведена прямая l, параллельная BC.
а) Найдите расстояние от центра окружности, описанной около треугольника ABC до прямой l.
б) Найдите, в каком отношении прямая l делит площадь треугольника ABC.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
— 1‐го числа каждого месяца долг возрастает на 4% по сравнению с концом предыдущего месяца;
— со 2‐го по 14‐е число каждого месяца необходимо выплатить часть долга;
— 15‐го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15‐е число предыдущего месяца.
Известно, что в пятый месяц кредитования нужно выплатить 44 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
При каких значениях параметра a система
имеет единственное решение?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
В последовательности натуральных чисел каждый следующий член равен произведению суммы цифр предыдущего члена и
а) Найдите пятый член последовательности.
б) Найдите 50‐й член последовательности.
в) Вычислите сумму первых пятидесяти членов этой последовательности.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
23 декабря 2018
В закладки
Обсудить
Жалоба
Разбор всех заданий нового тренировочного варианта.
trvar255.pdf
Contents
- 1 Задание 1. Вариант 255 Ларина ЕГЭ 2019 по математике
- 1.1 Решение
- 2 Задание 2
- 2.1 Решение
- 3 Задание 3
- 3.1 Решение
- 4 Задание 4. Вариант 255 Ларина ЕГЭ 2019 по математике
- 4.1 Решение
- 5 Задание 5. Вариант 255 Ларина
- 5.1 Решение
- 6 Задание 6
- 6.1 Решение
- 7 Задание 7. Вариант 255 Ларина ЕГЭ 2019 по математике
- 7.1 Решение
- 8 Задание 8. Вариант 255 Ларина. ЕГЭ 2019 по математике.
- 8.1 Решение
- 9 Задание 9. Вариант 255 Ларина ЕГЭ 2019 по математике
- 9.1 Решение
- 10 Задание 10. Вариант 255 Ларина ЕГЭ 2019 по математике
- 10.1 Решение
- 11 Задание 11
- 11.1 Решение
- 12 Задание 12
- 12.1 Решение
- 13 Задание 13. Вариант 255 Ларина. ЕГЭ 2019 по математике.
- 13.1 Решение
- 14 Задание 14. Вариант 255 Ларина ЕГЭ 2019 по математике
- 14.1 Решение
- 15 Задание 15
- 15.1 Решение
- 16 Задание 16
- 16.1 Решение
- 17 Задание 17
- 17.1 Решение
- 18 Задание 18. Вариант 255 Ларина
- 18.1 Решение
- 19 Задание 19. ЕГЭ 2019 по математике.
- 19.1 Решение
- 20 Видео: Разбор Варианта ЕГЭ Ларина №255 (№1-15)
- 21 Видео: Разбор Варианта ЕГЭ Ларина №255 (№16-19)
Поезд Новосибирск‐Красноярск отправляется в 15:20 а прибывает в 4:20 на следующий день (время московское). Сколько часов поезд находится в пути?
Решение
Ответ: 13.
Задание 2
На диаграмме показано распределение выплавки меди в странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место по выплавке меди занимали США, десятое место — Казахстан. Какое место занимала Индонезия?
Решение
Из графика следует, что Индонезия занимает пятое место.
Ответ: 5.
Задание 3
На координатной плоскости изображён параллелограмм. Найдите его площадь.
Решение
Площадь параллелограмма равна:
Ответ: 7.
Задание 4. Вариант 255 Ларина ЕГЭ 2019 по математике
Во время психологического теста психолог предлагает каждому из двух испытуемых А. и Б. выбрать одну из трех цифр: 1, 2 или 3. Считая, что все комбинации равновозможные, найдите вероятность того, что А. и Б. выбрали разные цифры. Результат округлите до сотых
Решение
Всего возможных комбинаций:
9 — (11;12;13;21;22;23;31;32;33).
Разные цифры в 6 комбинациях:
Ответ: 0,67.
Задание 5. Вариант 255 Ларина
Решите уравнение:
Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Решение
Меньший из корней -6.
Ответ: -6.
Задание 6
На рисунке угол 1 равен 46° угол 2 равен 30° угол 3 равен 44° Найдите угол 4. Ответ дайте в градусах.
Решение
сумма углов в выпуклом четырехугольнике равна 360°.
Ответ: 120.
Задание 7. Вариант 255 Ларина ЕГЭ 2019 по математике
На рисунке изображен график функции f(x) . Касательная к этому графику, проведенная в точке с абсциссой −4, проходит через начало координат. Найдите f`(-4).
Решение
:
Ответ: 0,5.
Задание 8. Вариант 255 Ларина. ЕГЭ 2019 по математике.
Найдите квадрат расстояния между вершинами D и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
Решение
Ответ: 6.
Задание 9. Вариант 255 Ларина ЕГЭ 2019 по математике
Найдите значение выражения:
Решение
Задание 10. Вариант 255 Ларина ЕГЭ 2019 по математике
Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле: P = 4mg/πD², где m =1200 кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая ускорение свободного падения g =10 м/с , а π = 3, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400000 Па. Ответ выразите в метрах
Решение
Из формулы P = 4mg/πD² найдём D:
D = √((4*1200*10)/(400*3)) = √(4/100) = 0.2
Ответ: 0,2.
Задание 11
Игорь и Паша могут покрасить забор за часов. Паша и Володя могут покрасить этот же забор за 12 часов, а Володя и Игорь — за часов. За сколько часов мальчики покрасят забор, работая втроём?
Решение
Пусть x — производительность Игоря, y — Паши, z — Володи(в частях забора в час) . Весь забор примем за 1.
Ответ: 8.
Задание 12
Найдите наибольшее значение функции:
на отрезке [-9;-1].
Решение
Ответ: -6.
Задание 13. Вариант 255 Ларина. ЕГЭ 2019 по математике.
- а) Решите уравнение:
- б) Укажите корни этого уравнения, принадлежащие промежутку (-π/3; 2π]
Решение
Ответ:
Задание 14. Вариант 255 Ларина ЕГЭ 2019 по математике
Основание прямой призмы ABCA1B1C1 равнобедренный треугольник ABC, в котором AB = BC = 5, AC = 6. Высота призмы равна √ . На сторонах A1C1, A1B1 и AC выбраны соответственно точки D1, E1 и D так, что , , , , и через эти точки проведена плоскость.
- А) Найдите площадь сечения призмы этой плоскостью.
- Б) Найдите расстояние от точки A до плоскости сечения.
Решение
Ответ: а) 329/30; б) 3√6/7
Задание 15
Решите неравенство:
Решение
Ответ:
Задание 16
Дан треугольник АВС, в котором АВ = ВС = 5, медиана AD = √97/2. На биссектрисе СЕ выбрана точка F такая, что CE = 5CF. Через точку F проведена прямая l, параллельная ВС.
- А) Найдите расстояние от центра окружности, описанной около треугольника АВС до прямой l.
- Б) Найдите в каком отношении прямая l делит площадь треугольника АВС.
Решение
Ответ: А) Б)
Задание 17
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы: — 1‐го числа каждого месяца долг возрастает на 4 % по сравнению с концом предыдущего месяца; — со 2‐го по 14‐е число каждого месяца необходимо выплатить часть долга; — 15‐го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15‐е число предыдущего месяца. Известно, что в пятый месяц кредитования нужно выплатить 44 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решение
Пусть S — сумма кредита в тыс. руб. , n = 9 — число месяцев, r = 4%. Кредит на 9 месяцев, следовательно, по основной част долга ежемесячный платеж S/9.
| Месяц | Долг на начало месяца | Начисленный процент | Итоговый платеж |
| 1 | S | ||
| 2 | S — | ||
| 3 | |||
| 5 | |||
| 9 |
Задание 18. Вариант 255 Ларина
При каких значениях параметра a система:
имеет единственное решение
Решение
Пусть m = y-a; n = x-a, тогда имеем
Рассмотрим раскрытие модулей:
Построим график m(n). С учетом , что m = y-a и n = y-a , то график y(x) будет строиться смещение вершины (0;0) на (a;a) ( по прямой (y=x)), и построим график — cуществует 2 случая с одним решением :
1) При a=2.
2) При пересечении вершиной и диагональю y=x части графика она задается y = 16-2x).
Ответ: 2;
Задание 19. ЕГЭ 2019 по математике.
В последовательности натуральных чисел a1=47, каждый следующий член равен произведению суммы цифр предыдущего члена и a1 А) Найдите пятый член последовательности Б) Найдите 50‐й член последовательности В) Вычислите сумму первых пятидесяти членов этой последовательности..
Решение
A)
Б) вычислим еще несколько членов.
Ответ: А)752; Б)940; В)34404.
Видео: Разбор Варианта ЕГЭ Ларина №255 (№1-15)
Разбор Варианта Ларина №255 ЕГЭ математике профиль. Варианты ЕГЭ по математике профильный уровень 2019. Решение варианта Ларина. mrMathlesson Виктор Осипов
1-15 задания
16-19 задания
Смотрите также:
Разбор Варианта ЕГЭ по математике профиль Ларина #255. Полный разбор заданий ЕГЭ по математике 2019. Тренировочные варианты егэ по математике 2019. Математикс
№1-15
№16-19
Смотрите также: