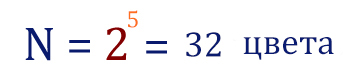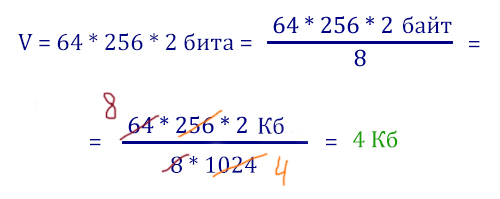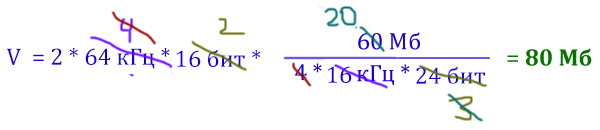7 июня 2016
В закладки
Обсудить
Жалоба
Фотографии заданий профильного ЕГЭ по математике с экзамена
Фотографии одного варианта.
Разбор ещё двух вариантов с экзамена:
6 июня
29 июня
Мы не можем точно утверждать о том, реальный ли это вариант с экзамена.
I have taught TOEFL in MOSCOW for more than 11 years. I have learned many tips and techniques about how to earn a high TOEFL score. One of the most difficult parts in every TOELF test is its speaking part. It consists of 6 questions. It is not enough just to speak English well to get the maximum points possible on the test.
Обучаю разговорному английскому. Помогу Вам подготовиться к TOEFL или ЕГЭ.
За полгода вывожу ученика начального уровня на уровень уверенного общения, свободного выражения своих мыслей. Специализируюсь на экспресс-методах обучения.
Экзаменационная работа профильного уровня длится 3 часа 55 минут (235 минут).
Минимальный порог — 27 баллов.
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и числу заданий.
Определяющим признаком каждой части работы является форма заданий:
- часть 1 содержит 8 заданий (задания 1-8) с кратким ответом в виде целого числа или конечной десятичной дроби;
- часть 2 содержит 4 задания (задания 9-12) с кратким ответом в виде целого числа или конечной десятичной дроби и 7 заданий (задания 13–19) с развернутым ответом (полная запись решения с обоснованием выполненных действий).

«Для того чтобы получить школьный аттестат, выпускнику необходимо сдать два обязательных экзамена в форме ЕГЭ, один из которых математика. В соответствии с Концепцией развития математического образования в Российской Федерации ЕГЭ по математике разделен на два уровня: базовый и профильный. Сегодня мы рассмотрим варианты профильного уровня».
Задание № 1 — проверяет у участников ЕГЭ умение применять навыки, полученные в курсе 5 — 9 классов по элементарной математике, в практической деятельности. Участник должен владеть вычислительными навыками, уметь работать с рациональными числами, уметь округлять десятичные дроби, уметь переводить одни единицы измерения в другие.
Пример 1.
В квартире, где проживает Петр, установили прибор учета расхода холодной воды (счетчик). Первого мая счетчик показывал расход 172 куб. м воды, а первого июня — 177 куб. м. Какую сумму должен заплатить Петр за холодную воду за май, если цена 1 куб. м холодной воды составляет 34 руб 17 коп? Ответ дайте в рублях.
Решение:
1) Найдем количество потраченной воды за месяц:
177 — 172 = 5 (куб м)
2) Найдем сколько денег заплатят за потраченную воду:
34,17 · 5 = 170,85 (руб)
Ответ: 170,85.
Задание № 2 —является одним из простейших заданий экзамена. С ней успешно справляется большинство выпускников, что свидетельствует о владении определением понятия функции. Тип задания № 2 по кодификатору требований — это задание на использования приобретённых знаний и умений в практической деятельности и повседневной жизни. Задание № 2 состоит из описания с помощью функций различных реальных зависимостей между величинами и интерпретация их графиков. Задание № 2 проверяет умение извлекать информацию, представленную в таблицах, на диаграммах, графиках. Выпускникам нужно уметь определять значение функции по значению аргумента при различных способах задания функции и описывать поведение и свойства функции по её графику. Также необходимо уметь находить по графику функции наибольшее или наименьшее значение и строить графики изученных функций. Допускаемые ошибки носят случайный характер в чтении условия задачи, чтении диаграммы.
#ADVERTISING_INSERT#
Задание № 2 проверяет умение читать диаграммы.
Пример 2. На рисунке показано изменение биржевой стоимости одной акции добывающей компании в первой половине апреля 2017 года. 7 апреля бизнесмен приобрёл 1000 акций этой компании. 10 апреля он продал три четверти купленных акций, а 13 апреля продал все оставшиеся. Сколько потерял бизнесмен в результате этих операций?
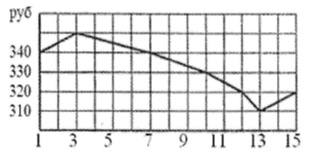
Решение:
1) 340 · 1000 = 340000 (руб) — бизнесмен потратил 7 апреля при покупке 1000 акций.
2) 1000 · 3/4 = 750 (акций) — составляют 3/4 от всех купленных акций.
3) 330 · 750 = 247500 (руб) — бизнесмен получил 10 апреля после продажи 750 акций.
4) 1000 – 750 = 250 (акций) — остались после продажи 750 акций 10 апреля.
5) 310 · 250 = 77500 (руб) — бизнесмен получил 13 апреля после продажи 250 акций.
6) 247500 + 77500 = 325000 (руб) — бизнесмен получил после продажи 1000 акций.
7) 340000 – 325000 = 15000 (руб) — потерял бизнесмен в результате всех операций.
Ответ: 15000.
Задание № 3 — является заданием базового уровня первой части, проверяет умения выполнять действия с геометрическими фигурами по содержанию курса «Планиметрия». В задании 3 проверяется умение вычислять площадь фигуры на клетчатой бумаге, умение вычислять градусные меры углов, вычислять периметры и т.п.
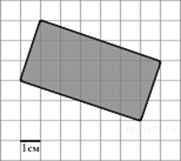
Пример 3. Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение: Для вычисления площади данной фигуры можно воспользоваться формулой Пика:
|
На рисунке справа B = 7 (красные точки), Г = 8 (зелёные точки),
Для вычисления площади данного прямоугольника воспользуемся формулой Пика: где В = 10, Г = 6, поэтому Ответ: 20. |
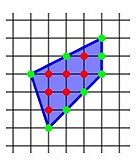
|
Читайте также: ЕГЭ по физике: решение задач о колебаниях
Задание № 4 — задача курса «Теория вероятностей и статистика». Проверяется умение вычислять вероятность события в простейшей ситуации.
Пример 4. На окружности отмечены 5 красных и 1 синяя точка. Определите, каких многоугольников больше: тех, у которых все вершины красные, или тех, у которых одна из вершин синяя. В ответе укажите, на сколько одних больше, чем других.
Решение: 1) Воспользуемся формулой числа сочетаний из n элементов по k:
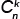 = =
|
n! | . |
| k!(n – k)! |
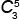 = =
|
5! | = | 3! · 4 · 5 | = | 4 · 5 | = 10 треугольников, |
| 3!(5 – 3)! | 3!2! | 1 · 2 |
у которых все вершины красные.
2)
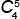 = =
|
5! | = | 4! · 5 | = 5 треугольников, |
| 4!(5 – 4)! | 4!1! |
у которых все вершины красные.
3) Один пятиугольник, у которого все вершины красные.
4) 10 + 5 + 1 = 16 многоугольников, у которых все вершины красные.
5)
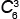 = =
|
6! | = | 3! · 4 · 5 · 6 | = | 4 · 5 · 6 | = 20 треугольников, |
| 3!(6 – 3)! | 3!3! | 1 · 2 · 3 |
у которых вершины красные или с одной синей вершиной.
6)
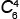 = =
|
6! | = | 4! · 5 · 6 | = | 5 · 6 | = 15 четырёхуголников, |
| 4!(6 – 4)! | 4!2! | 1 · 2 |
у которых вершины красные или с одной синей вершиной.
7)
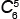 = =
|
6! | = | 5! · 6 | = 6 пятиугольников, |
| 5!(6 – 5)! | 5!1! |
у которых вершины красные или с одной синей вершиной.
Один шестиуголник, у которого вершины красные с одной синей вершиной.
9) 20 + 15 + 6 + 1 = 42 многоуголника, у которых все вершины красные или с одной синей вершиной.
10) 42 – 16 = 26 многоугольников, в которых используется синяя точка.
11) 26 – 16 = 10 многоугольников – на сколько многоугольников, у которых одна из вершин — синяя точка, больше, чем многоугольников, у которых все вершины только красные.
Ответ: 10.
Задание № 5 — базового уровня первой части проверяет умения решать простейшие уравнения (иррациональные, показательные, тригонометрические, логарифмические).
Пример 5. Решите уравнение 23 + x = 0,4 · 53 + x.
Решение. Разделим обе части данного уравнения на 53 + х ≠ 0, получим
| 23 + x | = 0,4 или |
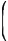
|
2 |

|
3 + х | = | 2 | , |
| 53 + х | 5 | 5 |
откуда следует, что 3 + x = 1, x = –2.
Ответ: –2.
Задание № 6 по планиметрии на нахождение геометрических величин (длин, углов, площадей), моделирование реальных ситуаций на языке геометрии. Исследование построенных моделей с использованием геометрических понятий и теорем. Источником трудностей является, как правило, незнание или неверное применение необходимых теорем планиметрии.
Пример 6. Площадь треугольника ABC равна 129. DE – средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.
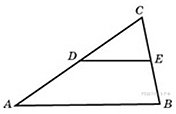
Решение. Треугольник CDE подобен треугольнику CAB по двум углам, так как угол при вершине C общий, угол СDE равен углу CAB как соответственные углы при DE || AB секущей AC. Так как DE – средняя линия треугольника по условию, то по свойству средней линии | DE = (1/2)AB. Значит, коэффициент подобия равен 0,5. Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому
| SΔCDE | = |
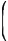
|
2 |

|
2 | ; SΔCDE = | 1 | · 129 = 32,25. |
| SΔCAB | 5 | 4 |
Следовательно, SABED = SΔABC – SΔCDE = 129 – 32,25 = 96,75.
Ответ: 96,75.
Смотреть вебинары по алгебре
Задание № 7 — проверяет применение производной к исследованию функции. Для успешного выполнения необходимо содержательное, не формальное владение понятием производной.
Пример 7. К графику функции y = f(x) в точке с абсциссой x0 проведена касательная, которая перпендикулярна прямой, проходящей через точки (4; 3) и (3; –1) этого графика. Найдите f′(x0).
Решение. 1) Воспользуемся уравнением прямой, проходящей через две заданные точки и найдём уравнение прямой, проходящей через точки (4; 3) и (3; –1).
(y – y1)(x2 – x1) = (x – x1)(y2 – y1)
(y – 3)(3 – 4) = (x – 4)(–1 – 3)
(y – 3)(–1) = (x – 4)(–4)
–y + 3 = –4x + 16| · (–1)
y – 3 = 4x – 16
y = 4x – 13, где k1 = 4.
2) Найдём угловой коэффициент касательной k2, которая перпендикулярна прямой y = 4x – 13, где k1 = 4, по формуле:
| k1 · k2 = –1, k2 = | –1 | –0,25. |
| 4 |
3) Угловой коэффициент касательной – производная функции в точке касания. Значит, f′(x0) = k2 = –0,25.
Ответ: –0,25.
Задание № 8 — проверяет у участников экзамена знания по элементарной стереометрии, умение применять формулы нахождения площадей поверхностей и объемов фигур, двугранных углов, сравнивать объемы подобных фигур, уметь выполнять действия с геометрическими фигурами, координатами и векторами и т.п.
Пример 8. Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.
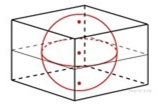
Решение. 1) Vкуба = a3 (где а – длина ребра куба), поэтому
а3 = 216
а = 3√216
a = 6.
2) Так как сфера вписана в куб, значит, длина диаметра сферы равна длине ребра куба, поэтому d = a, d = 6, d = 2R, R = 6 : 2 = 3.
Ответ: 3.
Приемы подготовки к профильному ЕГЭ по математике
Задание № 9 — требует от выпускника навыков преобразования и упрощения алгебраических выражений. Задание № 9 повышенного уровня сложности с кратким ответом. Задания из раздела «Вычисления и преобразования» в ЕГЭ подразделяются на несколько видов:
-
преобразования числовых рациональных выражений;
-
преобразования алгебраических выражений и дробей;
-
преобразования числовых/буквенных иррациональных выражений;
-
действия со степенями;
-
преобразование логарифмических выражений;
- преобразования числовых/буквенных тригонометрических выражений.
Пример 9. Вычислите tgα, если известно, что cos2α = 0,6 и
Решение. 1) Воспользуемся формулой двойного аргумента: cos2α = 2 cos2α – 1 и найдём
| cos2α = | cos2α + 1 | = | 0,6 + 1 | = | 1,6 | = 0,8. |
| 2 | 2 | 2 |
2) Воспользуемся формулой тригонометрических функций одного угла:
и найдём
| tg2α = | 1 | – 1 = | 1 | – 1 = | 10 | – 1 = | 5 | – 1 = 1 | 1 | – 1 = | 1 | = 0,25. |
| cos2α | 0,8 | 8 | 4 | 4 | 4 |
Значит, tg2α = ± 0,5.
3) По условию
значит, α – угол II четверти и tgα < 0, поэтому tgα = –0,5.
Ответ: –0,5.
#ADVERTISING_INSERT#
Задание № 10 — проверяет у учащихся умение использовать приобретенные раннее знания и умения в практической деятельности и повседневной жизни. Можно сказать, что это задачи по физике, а не по математике, но все необходимые формулы и величины даны в условии. Задачи сводятся к решению линейного или квадратного уравнения, либо линейного или квадратного неравенства. Поэтому необходимо уметь решать такие уравнения и неравенства, и определять ответ. Ответ должен получиться в виде целого числа или конечной десятичной дроби.
Пример 10. Два тела массой m = 2 кг каждое, движутся с одинаковой скоростью v = 10 м/с под углом 2α друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением Q = mv2sin2α. Под каким наименьшим углом 2α (в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 50 джоулей?
Решение. Для решения задачи нам необходимо решить неравенство Q ≥ 50, на интервале 2α ∈ (0°; 180°).
mv2sin2α ≥ 50
2· 102sin2α ≥ 50
200 · sin2α ≥ 50
Решением данного неравенства являются два неравенства:
| sinα ≥ | 1 | и sinα ≤ – | 1 | . |
| 2 | 2 |
Так как α ∈ (0°; 90°), то будем решать только
Неравенство
мы не рассматриваем, так как α для него будет более 180°. Итак:
Изобразим решение неравенства графически:
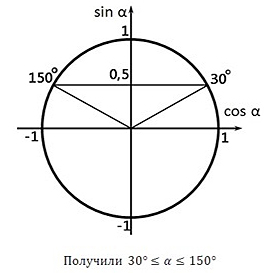
Так как по условию α ∈ (0°; 90°), значит 30° ≤ α < 90°. Получили, что наименьший угол α равен 30°, тогда наименьший угол 2α = 60°.
Ответ: 60.
Скачать бесплатно рабочие программы по алгебре
Задание № 11 — является типовым, но оказывается непростым для учащихся. Главным источником затруднений является построение математической модели (составление уравнения). Задание № 11 проверяет умение решать текстовые задачи.
Пример 11. На весенних каникулах 11-классник Вася должен был решить 560 тренировочных задач для подготовки к ЕГЭ. 18 марта в последний учебный день Вася решил 5 задач. Далее ежедневно он решал на одно и то же количество задач больше по сравнению с предыдущим днём. Определите, сколько задач Вася решил 2 апреля в последний день каникул.
Решение:
Обозначим a1 = 5 – количество задач, которые Вася решил 18 марта, d – ежедневное количество задач, решаемых Васей, n = 16 – количество дней с 18 марта по 2 апреля включительно, S16 = 560 – общее количество задач, a16 – количество задач, которые Вася решил 2 апреля. Зная, что ежедневно Вася решал на одно и то же количество задач больше по сравнению с предыдущим днём, то можно использовать формулы нахождения суммы арифметической прогрессии:
560 = (5 + a16) · 8,
5 + a16 = 560 : 8,
5 + a16 = 70,
a16 = 70 – 5
a16 = 65.
Значит, Вася решил 2 апреля 65 задач.
Ответ: 65.
Задание № 12 — проверяют у учащихся умение выполнять действия с функциями, уметь применять производную к исследованию функции.
Пример 12. Найти точку максимума функции y = 10ln(x + 9) – 10x + 1.
Решение: 1) Найдем область определения функции: x + 9 > 0, x > –9, то есть x ∈ (–9; ∞).
2) Найдем производную функции:
3) Найдем нули производной:
| y′= 0, | 10 | – 10 = 0, x = –8. |
| x + 9 |
4) Найденная точка принадлежит промежутку (–9; ∞). Определим знаки производной функции и изобразим на рисунке поведение функции:
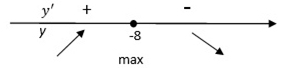
Искомая точка максимума x = –8.
Ответ: –8.
Скачать бесплатно рабочую программу по математике к УМК Мерзляка А.Г. 5-11 класс
Скачать бесплатно рабочую программу по математике к линии УМК Г.К. Муравина, К.С. Муравина, О.В. Муравиной 10-11
Скачать бесплатно методические пособия по алгебре
Задание № 13 — повышенного уровня сложности с развернутым ответом, проверяющее умение решать уравнения, наиболее успешно решаемое среди заданий с развернутым ответом повышенного уровня сложности.
Пример 13. а) Решите уравнение 2log32(2cosx) – 5log3(2cosx) + 2 = 0
б) Найдите все корни этого уравнения, принадлежащие отрезку 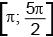
Решение: а) Пусть log3(2cosx) = t, тогда 2t2 – 5t + 2 = 0,
| откуда t = 2 или t = | 1 | . |
| 2 |

|
log3(2cosx) = | 2 | ⇔ |

|
2cosx = 9 | ⇔ |

|
cosx = | 4,5 | ⇔ т.к. |cosx| ≤ 1, |
| log3(2cosx) = | 1 | 2cosx = √3 | cosx = | √3 | ||||||
| 2 | 2 |

|
x = | π | + 2πk |
| 6 | |||
| x = – | π | + 2πk, k ∈ Z | |
| 6 |
б) Найдём корни, лежащие на отрезке 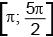
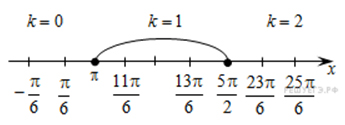
Из рисунка видно, что заданному отрезку принадлежат корни
| Ответ: а) | π | + 2πk; – | π | + 2πk, k ∈ Z; б) | 11π | ; | 13π | . |
| 6 | 6 | 6 | 6 |
Задание № 14 — повышенного уровня относится к заданиям второй части с развернутым ответом. Задание проверяет умения выполнять действия с геометрическими фигурами. Задание содержит два пункта. В первом пункте задание нужно доказать, а во втором пункте вычислить.
Пример 14. Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Расстояние между хордами равно 2√197.
а) Докажите, что центры оснований цилиндра лежат по одну сторону от этой плоскости.
б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
Решение: а) Хорда длиной 12 находится на расстоянии 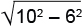

Тогда расстояние между хордами составляет либо
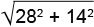
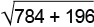
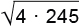
либо



По условию реализовался второй случай, в нем проекции хорд лежат по одну сторону от оси цилиндра. Значит, ось не пересекает данную плоскость в пределах цилиндра, то есть основания лежат по одну сторону от нее. Что требовалось доказать.
б) Обозначим центры оснований за О1 и О2. Проведем из центра основания с хордой длины 12 серединный перпендикуляр к этой хорде (он имеет длину 8, как уже отмечалось) и из центра другого основания — к другой хорде. Они лежат в одной плоскости β, перпендикулярной этим хордам. Назовем середину меньшей хорды B, большей A и проекцию A на второе основание — H (H ∈ β). Тогда AB,AH ∈ β и значит, AB,AH перпендикулярны хорде, то есть прямой пересечения основания с данной плоскостью.
Значит, искомый угол равен
| ∠ABH = arctg | AH | = arctg | 28 | = arctg14. |
| BH | 8 – 6 |
Ответ: arctg 14.
Подготовка к ОГЭ и ЕГЭ для учителей по алгебре
Задание № 15 — повышенного уровня сложности с развернутым ответом, проверяет умение решать неравенства, наиболее успешно решаемое среди заданий с развернутым ответом повышенного уровня сложности.
Пример 15. Решите неравенство |x2 – 3x| · log2(x + 1) ≤ 3x – x2.
Решение: Областью определения данного неравенства является интервал (–1; +∞). Рассмотри отдельно три случая:
1) Пусть x2 – 3x = 0, т.е. х = 0 или х = 3. В этом случае данное неравенство превращается в верное, следовательно, эти значения входят в решение.
2) Пусть теперь x2 – 3x > 0, т.е. x ∈ (–1; 0) ∪ (3; +∞). При этом данное неравенство можно переписать в виде (x2 – 3x) · log2(x + 1) ≤ 3x – x2 и разделить на положительное выражение x2 – 3x. Получим log2(x + 1) ≤ –1, x + 1 ≤ 2–1, x ≤ 0,5 –1 или x ≤ –0,5. Учитывая область определения, имеем x ∈ (–1; –0,5].
3) Наконец, рассмотрим x2 – 3x < 0, при этом x ∈ (0; 3). При этом исходное неравенство перепишется в виде (3x – x2) · log2(x + 1) ≤ 3x – x2. После деления на положительное выражение 3x – x2, получим log2(x + 1) ≤ 1, x + 1 ≤ 2, x ≤ 1. Учитывая область, имеем x ∈ (0; 1].
Объединяя полученные решения, получаем x ∈ (–1; –0.5] ∪ [0; 1] ∪ {3}.
Ответ: (–1; –0.5] ∪ [0; 1] ∪ {3}.
Задание № 16 — повышенного уровня относится к заданиям второй части с развернутым ответом. Задание проверяет умения выполнять действия с геометрическими фигурами, координатами и векторами. Задание содержит два пункта. В первом пункте задание нужно доказать, а во втором пункте вычислить.
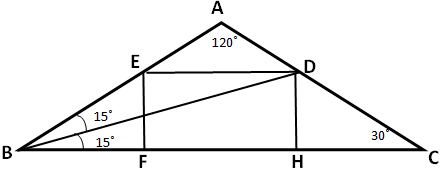
Пример 16. В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BD. В треугольник ABC вписан прямоугольник DEFH так, что сторона FH лежит на отрезке BC, а вершина E – на отрезке AB. а) Докажите, что FH = 2DH. б) Найдите площадь прямоугольника DEFH, если AB = 4.
Решение: а)
1) ΔBEF – прямоугольный, EF⊥BC, ∠B = (180° – 120°) : 2 = 30°, тогда EF = 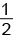
2) Пусть EF = DH = x, тогда BE = 2x, BF = x√3 по теореме Пифагора.
3) Так как ΔABC равнобедренный, значит, ∠B = ∠C = 30˚.
BD – биссектриса ∠B, значит ∠ABD = ∠DBC = 15˚.
4) Рассмотрим ΔDBH – прямоугольный, т.к. DH⊥BC.
| tg 15° = tg(45° – 30°) = | 3 – √3 | , |
| 3 + √3 |
| 3 – √3 | , | x |
| 3 + √3 | x√3 + FH |
(x√3 + FH)(3 – √3) = x(3 + √3)
2√3x – 6x = √3FH – 3FH
2x(√3 – 3) = FH(√3 – 3)
FH = 2x
FH = 2DH
Что требовалось доказать.
б) 1) ΔAED ∼ ΔABC по двум углам, так как ∠B – общий, ∠AED = ∠ABC как соответственные при ED || BC секущей AB. Из подобия треугольников следует:
√3 – 1 = 2 – x
x = 3 – √3
EF = 3 – √3
2) SDEFH = ED · EF = (3 – √3) · 2(3 – √3)
SDEFH = 24 – 12√3.
Ответ: 24 – 12√3.
Задание № 17 — задание с развернутым ответом, это задание проверяет применение знаний и умений в практической деятельности и повседневной жизни, умение строить и исследовать математические модели. Это задание — текстовая задача с экономическим содержанием.
Пример 17. Вклад в размере 20 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме того, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на х млн. рублей, где х — целое число. Найдите наибольшее значение х, при котором банк за четыре года начислит на вклад меньше 17 млн рублей.
Решение: В конце первого года вклад составит 20 + 20 · 0,1 = 22 млн рублей, а в конце второго – 22 + 22 · 0,1 = 24,2 млн рублей. В начале третьего года вклад (в млн рублей) составит (24,2 + х), а в конце — (24,2 + х) + (24,2 + х) · 0,1 = (26,62 + 1,1х). В начале четвёртого года вклад составит (26,62 + 2,1х), а в конце — (26,62 + 2,1х) + (26,62 + 2,1х) · 0,1 = (29,282 + 2,31х). По условию, нужно найти наибольшее целое х, для которого выполнено неравенство
(29,282 + 2,31x) – 20 – 2x < 17
29,282 + 2,31x – 20 – 2x < 17
0,31x < 17 + 20 – 29,282
0,31x < 7,718
Наибольшее целое решение этого неравенства — число 24.
Ответ: 24.
Задание № 18 — задание повышенного уровня сложности с развернутым ответом. Это задание предназначено для конкурсного отбора в вузы с повышенными требованиями к математической подготовке абитуриентов. Задание высокого уровня сложности — это задание не на применение одного метода решения, а на комбинацию различных методов. Для успешного выполнения задания 18 необходим, кроме прочных математических знаний, также высокий уровень математической культуры.
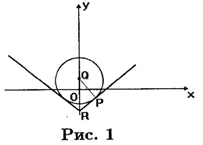
Пример 18. При каких a система неравенств
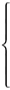 |
x2 + y2 ≤ 2ay – a2 + 1 |
| y + a ≤ |x| – a |
имеет ровно два решения?
Решение: Данную систему можно переписать в виде
 |
x2 + (y – a)2 ≤ 1 |
| y ≤ |x| – a |
Если нарисовать на плоскости множество решений первого неравенства, получится внутренность круга (с границей) радиуса 1 с центром в точке (0, а). Множество решений второго неравенства – часть плоскости, лежащая под графиком функции y = |x| – a,причём последний есть график функции
y = |x|, сдвинутый вниз на а. Решение данной системы есть пересечение множеств решений каждого из неравенств.
Следовательно, два решения данная система будет иметь лишь в случае, изображённом на рис. 1.
Точки касания круга с прямыми и будут двумя решениями системы. Каждая из прямых наклонена к осям под углом 45°. Значит, треугольник PQR – прямоугольный равнобедренный. Точка Q имеет координаты (0, а), а точка R – координаты (0, –а). Кроме того, отрезки PR и PQ равны радиусу окружности, равному 1. Значит,
Перейти в каталог продукции по алгебре
Задание № 19 — задание повышенного уровня сложности с развернутым ответом. Это задание предназначено для конкурсного отбора в вузы с повышенными требованиями к математической подготовке абитуриентов. Задание высокого уровня сложности — это задание не на применение одного метода решения, а на комбинацию различных методов. Для успешного выполнения задания 19 необходимо уметь осуществлять поиск решения, выбирая различные подходы из числа известных, модифицируя изученные методы.
Пример 19. Пусть Sn сумма п членов арифметической прогрессии (ап). Известно, что Sn + 1 = 2n2 – 21n – 23.
а) Укажите формулу п-го члена этой прогрессии.
б) Найдите наименьшую по модулю сумму Sn.
в) Найдите наименьшее п, при котором Sn будет квадратом целого числа.
Решение: а) Очевидно, что an = Sn – Sn – 1. Используя данную формулу, получаем:
Sn = S(n – 1) + 1 = 2(n – 1)2 – 21(n – 1) – 23 = 2n2 – 25n,
Sn – 1 = S(n – 2) + 1 = 2(n – 1)2 – 21(n – 2) – 23 = 2n2 – 25n + 27
значит, an = 2n2 – 25n – (2n2 – 29n + 27) = 4n – 27.
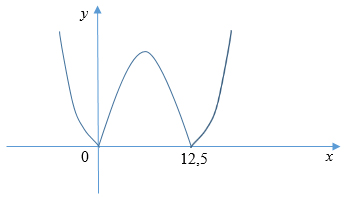
б) Так как Sn = 2n2 – 25n, то рассмотрим функцию S(x) = |2x2 – 25x|. Ее график можно увидеть на рисунке.
Очевидно, что наименьшее значение достигается в целочисленных точках, расположенных наиболее близко к нулям функции. Очевидно, что это точки х = 1, х = 12 и х = 13. Поскольку, S(1) = |S1| = |2 – 25| = 23, S(12) = |S12| = |2 · 144 – 25 · 12| = 12, S(13) = |S13| = |2 · 169 – 25 · 13| = 13, то наименьшее значение равно 12.
в) Из предыдущего пункта вытекает, что Sn положительно, начиная с n = 13. Так как Sn = 2n2 – 25n = n(2n – 25), то очевидный случай, когда данное выражение является полным квадратом, реализуется при n = 2n – 25, то есть при п = 25.
Осталось проверить значения с 13 до 25:
S13 = 13 · 1, S14 = 14 · 3, S15 = 15 · 5, S16 = 16 · 7, S17 = 17 · 9, S18 = 18 · 11, S19 = 19 · 13, S20 = 20 · 13, S21 = 21 · 17, S22 = 22 · 19, S23 = 23 · 21, S24 = 24 · 23.
Получается, что при меньших значениях п полный квадрат не достигается.
Ответ: а) an = 4n – 27; б) 12; в) 25.
Фото: nn.ucheba.ru
________________
*С мая 2017 года объединенная издательская группа «ДРОФА-ВЕНТАНА» входит в корпорацию «Российский учебник». В корпорацию также вошли издательство «Астрель» и цифровая образовательная платформа «LECTA». Генеральным директором назначен Александр Брычкин, выпускник Финансовой академии при Правительстве РФ, кандидат экономических наук, руководитель инновационных проектов издательства «ДРОФА» в сфере цифрового образования (электронные формы учебников, «Российская электронная школа», цифровая образовательная платформа LECTA). До прихода в издательство «ДРОФА» занимал позицию вице-президента по стратегическому развитию и инвестициям издательского холдинга «ЭКСМО-АСТ». Сегодня издательская корпорация «Российский учебник» обладает самым крупным портфелем учебников, включенных в Федеральный перечень — 485 наименований (примерно 40%, без учета учебников для коррекционной школы). Издательствам корпорации принадлежат наиболее востребованные российскими школами комплекты учебников по физике, черчению, биологии, химии, технологии, географии, астрономии — областям знаний, которые нужны для развития производственного потенциала страны. В портфель корпорации входят учебники и учебные пособия для начальной школы, удостоенные Премии Президента в области образования. Это учебники и пособия по предметным областям, которые необходимы для развития научно-технического и производственного потенциала России.
- История ЕГЭ
Сложные иллюстрации: цветной и ч/б вариант Архитектура, живопись, скульптура из сборников заданий ЕГЭ по истории.
Подборку составил Филинов Андрей Владимирович
Принцип создания слайдов:
Справа – изображение из варианта ЕГЭ (черно-белое)
Слева – цветная фотография объекта
→ скачать
Источник: vk.com/historystepa
Иногда в сборниках заданий попадаются такие некачественные изображения, что даже известные объекты культуры становятся трудноузнаваемыми.
Использованные сборники заданий:
1) ЕГЭ. История. Культура России. Учебный экзаменационный банк: учебная тетрадь / Под ред. И.А. Артасова. – М.: «Национальное образование», 2018.
2) Cборники 10, 30 типовых тренировочных экзаменационных вариантов И.А. Артасова, О.Н. и С.П. Мельниковых. М.: АСТ; Интеллект-Центр; «Национальное образование», «Экзамен». 2017, 2018.
3) ЕГЭ 2018. История. Тематический тренажёр. История российской культуры. Задания с иллюстративным материалом. / Е.А. Гевуркова, М.Н. Чернова. — М.: УЧПЕДГИЗ, 2018.
4) ЕГЭ 2017. Практикум по истории: История российской культуры: подготовка к выполнению заданий ЕГЭ / М. Н. Чернова. — М.: «Экзамен», 2017.
Связанные страницы:
Седьмое задание из ЕГЭ по информатике 2022. Отличное задание, которое нужно решать!
Данное задание проверяет умение определять объём памяти, необходимый для хранения графической и звуковой информации.
Приступим к примерным вариантам из ЕГЭ по информатике.
Задача (классика, количество цветов изображения)
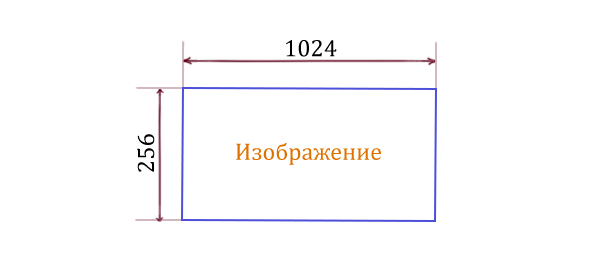
Какое максимальное количество цветов может быть в палитре неупакованного растрового изображения, имеющего размер 1024 * 256 пикселей и занимающего на диске не более 165 кб.
Решение:
1. Найдём сколько будет весить один пиксель! У нас всего 1024 * 256 пикселей. Берём максимально возможный объём картинки (165 Кб) и разделим его на количество пикселей.
Важно: Мы не пытаемся сразу вычислить, например, количество пикселей во всём изображении. А записываем сначала в виде действия 1024 * 256. Когда уже получается дробь, пытаемся сократить эту дробь по максимуму. Это позволяет экономить силы при решении седьмого задания из ЕГЭ по информатике 2022.
Нам нужно найти: сколько именно целых бит занимает один пиксель. Округляем количество бит в меньшую сторону, потому что мы не можем «перевалить» за максимальную отметку 165 Кб для всего изображения.
Применим формулу, которую нужно твёрдо знать для решения 7 задания из ЕГЭ по информатике.
Ответ: 32
Задача (Резервирование памяти)
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 64 * 256 пикселей при условии, что в изображении могут использоваться 4 различных цвета? В ответе запишите только целое число, единицу измерения писать не нужно.
Решение:
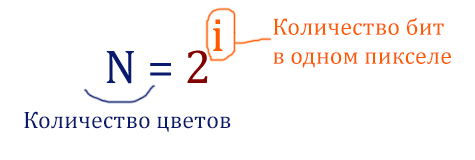
Задача обратная предыдущей. Первый вопрос на который нужно ответить: сколько весит 1 пиксель? Снова используется формула N = 2 i.
Видно, что 1 пиксель имеет объём i = 2 бита. Количество пикселей в изображении равно 64 * 256. Важно опять умножать эти два числа не сразу. Тогда объём картинки будет равен: количество пикселей (64 * 256) умножить на объём одного пикселя (2 бита).
В подобных задачах из ЕГЭ по информатике фишка в том, чтобы составить дробь и потом сократить её, тем самым вычисление делается без калькулятора и без лишних усилий.
Ответ: 4
Задача (работа со звуком)
Производится звукозапись музыкального фрагмента в формате квадро (четырёхканальная запись) с частотой дискретизации 16 кГц и 24-битным разрешением. Результаты записываются в файл, сжатие данных не производится; размер полученного файла 60 Мбайт. Затем производится повторная запись этого же фрагмента в формате стерео (двухканальная запись) с частотой дискретизации 64 кГц и 16-битным разрешением. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.
Решение:
Общая формула для решения 7-ого задания на тему звуковых файлов из ЕГЭ по информатике.
Её легко запомнить. Объём записанного файла равен произведению всех остальных параметров. Важно соблюдать единицы измерения.
Распишем формулу дискретизации для первой звукозаписи и для второй. В первом случае у нас режим квадро, значит, нужно к произведению добавить ещё 4. Во втором случае режим стерео, значит, должны поставить коэффициент 2. Т.к. производилась запись этого же фрагмента, то время в обоях случаях одинаковое.
Выражаем время из первого уравнения и подставляем во второе.
Опять удобно решать с помощью сокращение дробей.
Ответ: 80
Закрепим результат, решив ещё одну тренировочную задачу из ЕГЭ по информатике 2021.
Задача (ЕГЭ по информатике 2020, Досрочная волна)
Музыкальный фрагмент был записан в формате квадро (четырёхканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла без учёта размера заголовка файла – 12 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер в Мбайт файла, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно. Искомый объём не учитывает размера заголовка файла.
Решение:
Вначале выписываем формулу для первого файла и для второго файла. Подставляем всё, что нам известно.
Для второго звукового файла коэффициенты все переносим в одну сторону.
Выражаем из первого уравнения произведение M * i * t и подставляем его во второе уравнение.
После небольших сокращений получаем 4 Мб для второго звукового файла.
Время было для обоих файлов одинаковым, потому что было сказано, что тот же музыкальный файл перезаписали второй раз с другими параметрами.
Ответ: 4
Удачи при решении 7 задания из ЕГЭ по информатике 2022!
Особенности ЕГЭ по биологии
Год от года задания и требования к ответам усложняются. Причина в том, что экзамен по биологии — абитуриентский, он выявляет конкурентоспособность выпускников. Базовых знаний для него мало. Некоторые школьники сообщают учителям о желании сдавать ЕГЭ по биологии только за полгода до экзамена, а это очень недальновидно. Судя по тенденциям, даже подготовки на протяжении одиннадцатого класса скоро будет недостаточно.
Задания все чаще направлены на детализацию. Хотя выпускник должен давать лаконичные ответы, теперь многие вопросы подразумевают развернутый рассказ на ту или иную тему. К примеру, изображен человеческий мозг. На нем выделены отделы, которые нужно назвать и описать, указав особенности строения и функции. Конечно, в этом случае ученику необходимо дать подробный ответ, показать свое знание отделов головного мозга.
Из текста задания, как правило, понятно, на сколько вопросов ученик должен ответить. Но не всегда. При подготовке к экзамену рекомендуется сделать в тетради таблицу из двух столбцов и отмечать в ней знаками «+» и «-» вопросы из одного задания на которые получилось или не получилось ответить.
В этом году появились задания, которые могут показаться необычными. К примеру, на рисунке изображены скелет, отпечаток перьев и реконструкция животного, вымершего 150-147 млн лет назад. От ученика требуется по фрагменту геохронологической таблицы определить, в какой эре и в каком периоде обитал этот организм, ответить на сопутствующие вопросы. Новое задание подсказывает учителям, что в этом году очень важно проработать с учениками тему эволюции.
Темы заданий с рисунками
Действительно, можно выявить и проработать темы вопросов — они становятся известны благодаря демоверсии, экзаменам прошлых лет и учебным материалам, из которых составители ЕГЭ заимствуют формулировки. Рассмотрим подробнее примеры некоторых заданий с рисунками.
Деление клетки
- Пример 1. Показана фаза деления клетки — нужно это фазу назвать. Также необходимо указать предшествующую и будущую фазу, объяснить свой ответ.
В ЕГЭ предусмотрено много заданий, освещающих разные фазы митоза и мейоза. Ученик должен научиться определять эти фазы по рисунку, уметь различать: гомологичные или не гомологичные хромосомы участвуют в этом делении, какие из них попадают в новые клетки. Также нужно выучить отличия митоза от мейоза на каждой стадии процесса.
- Пример 2. Представлена фаза (профаза I) деления клеток. Необходимо назвать эту фазу и тип (мейоз) деления, ответ обосновать.
В данном примере нужно указать на конъюгацию и кроссинговер. Можно добавить про образование бивалентов. Также ученик должен прописать характерные признаки профазы I. Рисунки на тему митоза и мейоза встречаются в разных вариациях.

Биология. Общая биология. 11 класс. Базовый уровень. Рабочая тетрадь
Предлагаемая тетрадь — часть учебного комплекса к учебнику В.И. Сивоглазова, И.Б. Агафоновай, Е.Т. Захаровой «Биология. Общая биология. 11 класс». Учебник соответствует Федеральному государственному образовательному стандарту, рекомендован Министерством образования и науки РФ, включен в Федеральные перечень учебников.
Купить
Эмбриогенез
- Пример 1. В иллюстрации представлен процесс из цикла развития ланцетника. Ученику нужно назвать этот процесс, указать его особенности и чем он завершается.
- Пример 2. На рисунке изображена стадия эмбрионального развития ланцетника. Необходимо назвать эту стадию и структуры, обозначенные цифрами, а также пояснить, из каких зародышевых листков формируются данные структуры.
Существует много вариантов заданий, связанных с эмбриональным развитием. Во втором примере цифрами могут быть обозначены и энтодерма, и эктодерма, и мезодерма, и хорда, и нервная трубка и прочее. Эмбриогенез школьникам следует знать во всех подробностях.
Гаметогенез
- Пример. Ученик должен назвать процессы, которые проиллюстрированы схемами (например, сперматогенез, овогенез, оплодотворение) и объяснить различие между конечными результатами этих процессов.
Простой и распространенный вопрос, однако он может быть представлен в усложненном виде. С такими рисунками встречаются задания и другого типа, в которых нужно определить плоидность гамет на каждой стадии эмбриогенеза или овогенеза. Ученику понадобится знание терминологии, а также понимание отличий стадии роста от стадии размножения и созревания.
Строение растений
- Пример 1. Представлен поперечный срез листа — нужно указать структуры, обозначенные цифрами, и функции некоторых из этих структур.
- Пример 2. Даны поперечные срезы стеблей — требуется назвать классы представленных растений и объяснить, по каким признакам это было определено.
- Пример 3. Изображен срез стебля. Ученик должен обозначить его внутренние структуры и их функции.
Задания по ботанике часто встречаются в учебниках и будут широко представлены на экзамене. Ученику важно знать строение растений и, кроме того, уметь письменно объяснять функции тех или иных структур (с этим наблюдаются сложности).

ЕГЭ. Биология. Большой сборник тематических заданий для подготовки к единому государственному экзамену
Вниманию учащихся и учителей предлагается новое учебное пособие, которое поможет успешно подготовиться к единому государственному экзамену по биологии. Сборник содержит вопросы, подобранные по разделам и темам, проверяемым на ЕГЭ, и включает задания разных типов и уровней сложности. В конце пособия приводятся ответы на все задания. Предлагаемые тематические задания помогут учителю организовать подготовку к единому государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче выпускного экзамена. Книга адресована учащимся, учителям и методистам.
Купить
Отделы и классы растений
- Пример 1. Изображены два растения (например, мох кукушкин лен и хвощ полевой). От ученика требуется назвать отделы, к которым относятся эти растения и указать признаки, позволившие это определить.
- Пример 2. Представлены колос и его семя. Нужно указать, как какому отделу и классу относится изображенное растение, объяснить почему.
- Пример 3. Дан цветок класса двудольные, а также его кочан и плод в разрезе. Необходимо назвать класс и обосновать ответ, а также назвать представленные органы и указать их значения в жизни растения.
Тоже очень распространенные задания. Что касается семейств, их признаков и названий — это в заданиях не встречается, однако требует повторения. В ответах опять-таки важны нюансы: в третьем примере детям нужно указать (помимо прочего), что представлено двухлетнее растение, и что его зимовку обеспечивает кочан.
Жизненный цикл водоросли
- Пример. Изображен жизненный цикл Хламидомонады. Требуется указать названия стадий, обозначенных цифрами, а также объяснить, в результате какого деления образовались определенные клетки. Кроме того, ответит на вопрос: чем представлены гаметофит и спорофит этой зеленой водоросли?
Главная сложность задания — обозначить спорофит у Хламидомонады. Школьники плохо отличают споры от гамет. От учителя требуется доступно донести до учеников жизненный цикл растений, например, в форме такого алгоритма: у растений споры развиваются только мейозом, споры развиваются только из зиготы; у животных мейозом образуются гаметы; у растений гаметы образуются митозом. В задании на эту тему может встретиться какая угодно водоросль (спирогира, улотрикс и другие).
Органы слуха и зрения
- Пример 1. Дано изображение уха земноводного. Нужно назвать орган и его отделы, обозначенные цифрами. Далее — пояснить функции этих отделов и написать, у какого животного впервые сформировался один из отделов.
Рисунок к этому заданию редкий, его нет в учебниках. Когда учитель все-таки находит и показывает нужную иллюстрацию детям, они ее легко запоминают. Рассказ о функциях каждого отдела тоже дается ученикам легко. Следует предупредить детей, что не надо подробно рассказывать о вестибулярном аппарате, когда они расписываю функции внутреннего уха как части органа слуха.
- Пример 2. Представлено изображение глаза. Ученик должен написать, какие структуры глаза обозначены цифрами и функции этих структур.
Схематическое изображение органа зрения может сопровождать разные задания. Хотя вопросы на эту тему кажутся простыми, ученики все же допускают ошибки и неточности в ответах. Например, относят к оболочкам глаза стекловидное тело и хрусталик, не указывают, что радужная оболочка содержит пигмент, определяющий цвет глаза или что она является частью сосудистой оболочки, не относят роговицу к составу склеры. При подготовке эти нюансы лучше проговорить.

Биология. Общая биология.10-11 классы. Базовый уровень. Рабочая тетрадь
Тетрадь содержит различные творческие вопросы и задания, в том числе лабораторные работы, задачи, таблицы, схемы и рисунки, а также тестовые задания, которые помогут подготовиться к ЕГЭ.
Купить
Строение скелета
- Пример 1. На рисунке изображены кости таза и одной ноги человека. Ученик должен определить отдел скелета, обозначенный знаком вопроса (в данном случае тазовый пояс верхней конечности), указать, какими костями он образован, объяснить роль этого отдела.
На первый взгляд обычное задание. Однако таз часто ошибочно относят к свободной нижней конечности или просто к нижней конечности. Кроме того, дети не всегда дифференцирую кости таза. В прошлых ЕГЭ были очень распространены задания, включающие пояс верхних конечностей.
- Пример 2. Изображен скелет кита. Нужно указать, какие особенности строения скелета этого животного доказывают его наземное происхождение, привести доказательства. Также объяснить, с какой группой современных позвоночных животных у него проявляется сходство во внешнем строении и как называется эволюционный процесс, в результате которого сформировалось это сходство. Ответы обосновать.
Если с ответами по переднему поясу конечностей школьники справляются довольно хорошо, то с поясом задних конечностей (которые они, к тому же, часто называю нижними) дело обстоит хуже. Дети легко отмечают процесс конвергенции и указывают на сходство китообразных с рыбами, но далеко не все рассказывают о рудиментарном тазовом поясе.
Строение насекомых
- Пример 1. Изображены разные ротовые аппараты, которые нужно соотнести с кузнечиком, домовой мухой и комаром. Также от ученика требуется назвать типы этих аппаратов и объяснить, какой путь эволюции привел к образованию различных по строению ротовых аппаратов.
- Пример 2. На рисунке представлены конечности насекомых. Нужно найти среди них плавательную и бегательную, пояснить ответ, привести по одному примеру насекомых, у которых образовались такие конечности.
Эти задания в очередной раз показывают, что ЕГЭ этого года требует детализации знаний. Ученикам могут встретиться любые вопросы о строении членистоногих (в том числе паукообразных и ракообразных).
Строение кишечнополостных
- Пример. На рисунке изображена медуза аурелия. Необходимо указать особенности ее тела и органы, отмеченные цифрами. Также нужно назвать непосредственно тип животного и примеры других представителей этого типа.
В данном случае ребенку легко назвать тип животного. Но есть задания и сложнее, медуза не единственное кишечнополостное, представленное в вопросах с рисункам. Могут встретиться и гидра, и коралловые полипы.
В первой части ЕГЭ тоже есть задания с рисунками. В них часто проиллюстрированы вегетативные органы, покрытосеменные и голосеменные растения, мхи, папоротники, водоросли, отдельные органоиды клетки, схемы головного мозга и нервной системы, отделы пищеварительной системы. Среди изображений животных могут неожиданно оказаться фотографии козы, брюхоногого моллюска, паука, медузы, кольчатого червя.
При подготовке к экзамену важно использовать пособия с заданиями, максимально приближенными к вопросам ЕГЭ. Также важно приучить детей внимательно читать задания и давать подробные объяснения, если в них есть необходимость.
Обратите внимание на рабочую программу по биологии к УМК Пасечника В.В. 10-11 класс. Также замечательный материал для подготовки: рабочая программа к УМК Сонина Н.И. углубленного уровня для 10-11 классов.

ЕГЭ
ЕГЭ Профиль
Варианты Профильного ЕГЭ
ЕГЭ База