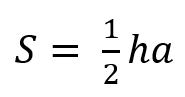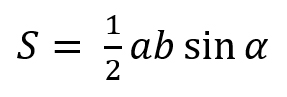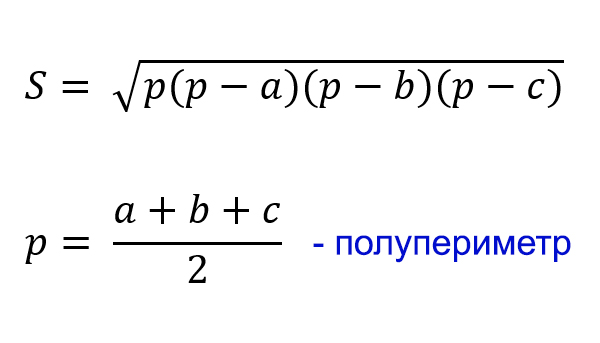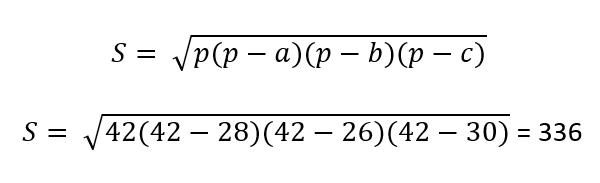Егэ формула герона - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Найдите площадь треугольника со сторонами 13, 14, 15.

Найдите радиус окружности, описанной вокруг треугольника со сторонами 13, 14 и 15.

Найдите третью сторону треугольника, если известно, что две другие равны 6 и 7, а площадь равна

Две стороны треугольника равны соответственно 5 и 8, а его площадь равна 12. Определите длину третьей стороны.

Найдите площадь ромба со стороной 5 и большей диагональю 8.

Пройти тестирование по этим заданиям

Источник

Привет! Это первая статья посвящённая ЕГЭ по математике профильного уровня.

В ней речь пойдёт о задачах на площадь треугольника.

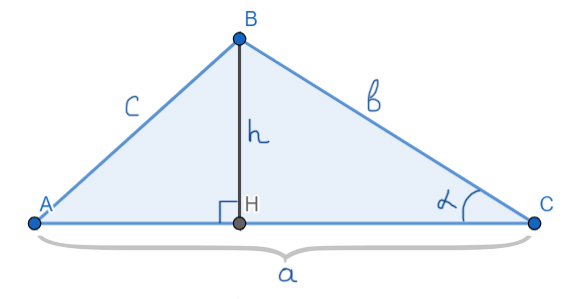
Вспомним основные формулы для площади треугольника.

Формулы для площади треугольника

Основная формула:

Площадь треугольника равна половине произведения основания на высоту.

Запасная формула:

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Формула Герона:

Решение задач

Приступим к тренировочным задачам задания №1 из ЕГЭ по математике профильного уровня на площадь треугольника.

Задача (Прямоугольный треугольник)

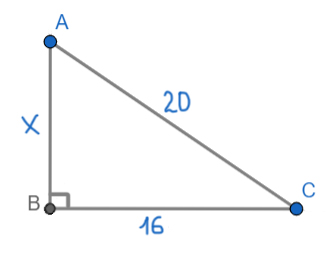
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 16 и 20.

Решение:

Здесь можно воспользоваться основной формулой для нахождения площади прямоугольного треугольника. Но важно знать, что любой катет — это и есть высота прямоугольного треугольника.

Таким образом, высота будет, к примеру, сторона AB. Тогда основанием будет сторона ВС.

Найдём сторону АВ по теореме Пифагора.

x² + 16² = 20²
x² = 400 — 256 = 144
x = 12

Тогда площадь будет равна:

S = 0,5 * 12 * 16 = 6 * 16 = 96

Ответ: 96

Задача (Прямоугольный треугольник, закрепление)

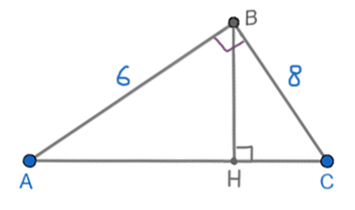
Катеты прямоугольного треугольника равны 6 и 8. Найдите высоту, проведённую к гипотенузе.

Решение:

Найдём гипотенузу по теореме Пифагора.

AC² = AB² + BC²
AC² = 6² + 8² = 100
AC = 10

Мы в прошлой задаче выяснили, что площадь прямоугольного треугольника можно найти, как половину произведения его катетов. А с другой стороны, исходя из основной формулы, площадь равна половине произведения высоты ВН и основания (гипотенузы AC).

S = 0,5*AB*BC = 0,5*BH*AC
BH = AB*BC / AC = 6*8 / 10 = 4,8

Ответ: 4,8

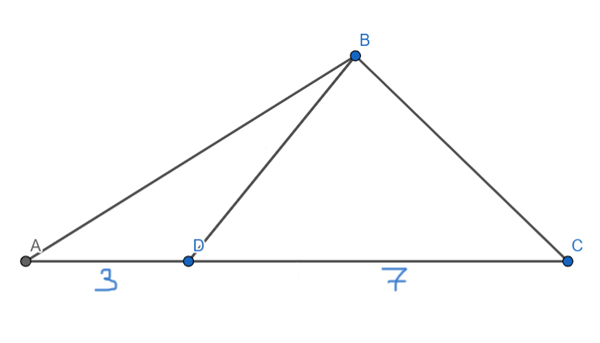
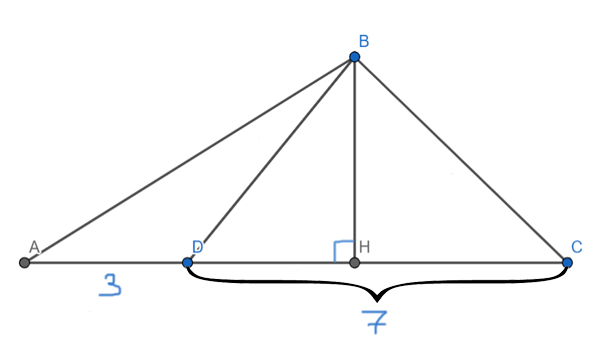
Задача (Три треугольника, одна высота)

На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7. Площадь треугольника ABC равна 100. Найдите площадь треугольника BCD.

Решение:

Проведём в треугольнике ABC высоту BH. Оказывается, что ВН является высотой и для треугольника ABD, и для треугольника DBC, и для треугольника ABC.

Применим основную формулу для треугольника ABC и найдём высоту BH.

S_ABC = 0,5 * AC *BH
S_ABC = 0,5 * 10 * BH = 100
BH = 100 / (0,5*10) = 20

Теперь применим основную формулу, чтобы найти площадь треугольника BCD.

S_DBC = 0,5 * DC * BH
S_DBC = 0,5 * 7 * 20 = 70

Ответ: 70

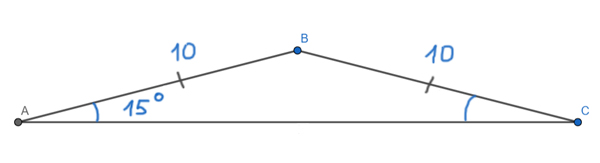
Задача (Запасная формула)

В равнобедренном треугольнике ABC (AB = BC) угол при основании равен 15°. Боковая сторона равна 10. Найдите площадь треугольника ABC.

Решение:

Здесь удобно использовать запасную формулу. Мы знаем две боковые стороны треугольника. Остаётся найти синус угла между ними.

Мы знаем, что углы при основании равны в равнобедренном треугольнике. Поэтому

∠ABC + ∠ВАС + ∠BCA = 180°
∠ABC = 180° — ∠ВАС — ∠BCA
∠ABC = 180° — 15° — 15° = 150°

Синус угла 150° известен. Он равен sin(150°) = sin(30°) = 0,5. Тогда

S = 0,5 * AB*BC * sin(∠ABC)
S = 0,5 * 10*10 * 0,5 = 25

Ответ: 25

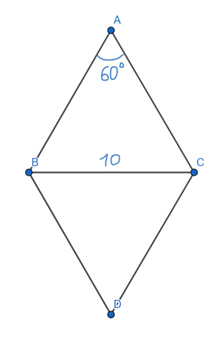
Задача (Треугольники в ромбе)

Найдите площадь ромба, если один из его углов равен 60°, а меньшая диагональ равна 10. В ответе запишите число, делённое на √3.

Решение:

Меньшая диагональ будет находится напротив угла 60°, т.к. второй угол у ромба будет 120°, и напротив этого угла будет находится большая диагональ.

Рассмотрим треугольник ВАС. Мы знаем, что у ромба все стороны равны, поэтому треугольник ВАС равносторонний. Ведь, ВА = АС ⇒ ∠ABC = ∠ACB. Тогда

∠ABC + ∠ACB + ∠BAC = 180°
x = ∠ABC = ∠ACB
x + x + 60° = 180°
2x = 120°
x = 60°

Значит, треугольник ВАС равносторонний. Следовательно, BA = AC = CB = 10.

Чтобы найти площадь ромба, можно разбить его на два одинаковых треугольника: BAC и BDC. Эти два треугольника равны по трём сторонам (BA = AC = CD = DB, BC — общая).

Площадь треугольника BAC легко найти по запасной формуле, ведь две стороны мы знаем, и синус угла между ними тоже известен.

S_BAC = 0,5 * BA * AC * sin(60°)
S_BAC = 0,5 * 10 * 10 * (√3/2)
S_BAC = 25 * √3

Площадь ромба будет равна

S_BACD = 2 * S_BAC = 2 * 25 * √3 = 50 * √3

В ответе нужно указать число, делённое на √3.

Ответ: 50

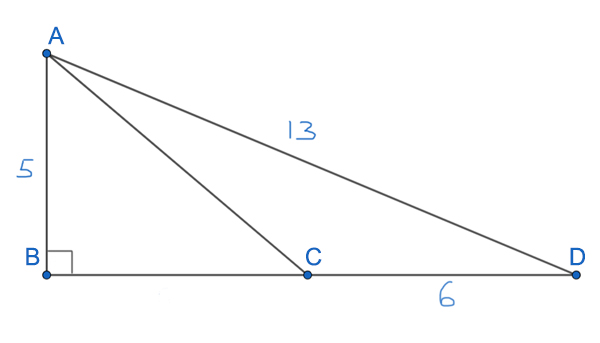
Задача (Решаем задачу двумя способами)

На рисунке AB ⊥ BD, AB = 5, AD = 13 и CD = 6. Найдите площадь треугольника CAD.

Решение:

Первый способ (основная формула)

Нам известна высота треугольника CAD, AB=5. Нам известно основание, на которое она опущена, это CD=6. Применим основную формулу для площади треугольника.

S_CAD = ½ * AB * CD
S_CAD = ½ * 5 * 6 = 15

Второй способ (запасная формула)

В прямоугольном треугольнике ABD найдём синус ∠BDA.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

sin(∠BDA) = AB/AD = 5/13

Теперь воспользуемся запасной формулой для треугольника CAD.

S_CAD = ½ * CD * DA * sin(∠BDA)
S_CAD = ½ * 6 * 13 * (5/13) = 15

Ответ: 15

Задача (Формула Герона)

Найдите площадь треугольника, стороны которого равны 28, 26, 30.

Решение:

Решим по формуле Герона.

Найдём полупериметр.

p=(28+26+30)/2 = 42

Тогда

Ответ: 336

На этом всё! Сегодня мы повторили основные формулы для нахождения площади треугольника и порешали задачи на эту темы. Всем удачи!

Источник

Ирина Алексеевна Антоненко

Эксперт по предмету «Геометрия»

Задать вопрос автору статьи

Предварительные сведения

Для начала введем сведения и обозначения, которые будут необходимы нам в дальнейшем.

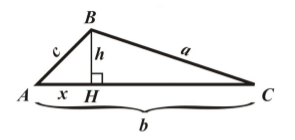
Будем рассматривать треугольник $ABC$ с острыми углами $A$ и $C$. Проведем в нем высоту $BH$. Введем следующие обозначения: $AB=c, BC=a, $$AC=b, AH=x, BH=h $(рис. 1).

Рисунок 1.

Введем без доказательств теорему о площади треугольника.

Теорема 1

Площадь треугольника определяется как половина произведения длины его стороны, на высоту, проведенную к ней, то есть

[S=frac{1}{2}bh]

Научись программировать

Получи навыки для отличной карьеры в IT под руководством ведущих экспертов

Выбрать занятия

Формула Герона

Введем и докажем теорему о нахождении площади треугольника по трем известным сторонам. Эта формула носит название формулы Герона.

Теорема 2

Пусть нам даны три стороны треугольника $a, b и c$. Тогда площадь этого треугольника выражается следующим образом

[S=sqrt{pleft(p-aright)left(p-bright)(p-c)}]

где $p$ — полупериметр данного треугольника.

Доказательство.

Будем пользоваться обозначениями, введенными на рисунке 1.

Рассмотрим треугольник $ABH$. По теореме Пифагора, получим

[h^2=c^2-x^2]

Очевидно, что $HC=AC-AH=b-x$

Рассмотрим треугольник $ CBH$. По теореме Пифагора, получим

[h^2=a^2-{HC}^2] [h^2=a^2-{(b-x)}^2] [h^2=a^2-b^2+2bx-x^2]

Приравняем значения квадрата высоты из двух полученных соотношений

[c^2-x^2=a^2-b^2+2bx-x^2] [2bx=c^2-a^2+b^2] [x=frac{c^2-a^2+b^2}{2b}]

Из первого равенства найдем высоту

[h^2=c^2-{left(frac{c^2-a^2+b^2}{2b}right)}^2] [h^2=frac{{4b^2c}^2-{left(c^2-a^2+b^2right)}^2}{4b^2}] [h^2=frac{left(2bc-c^2+a^2-b^2right)({2bc+c}^2-a^2+b^2)}{4b^2}] [h^2=frac{left(a^2-{left(c-bright)}^2right)({left(c+bright)}^2-a^2)}{4b^2}] [h^2=frac{left(a-c+bright)left(a+c-bright)left(c+b-aright)(c+b+a)}{4b^2}] [h^2=frac{(a+b+c)left(a+b+c-2cright)left(a+b+c-2bright)left(a+b+c-2aright)}{4b^2}]

Так как полупериметр равен $p=frac{a+b+c}{2}$, то есть $a+b+c=2p$, то

[h^2=frac{2pleft(2p-2cright)left(2p-2bright)left(2p-2aright)}{4b^2}] [h^2=frac{4pleft(p-aright)left(p-bright)left(p-cright)}{b^2}] [h=sqrt{frac{4pleft(p-aright)left(p-bright)left(p-cright)}{b^2}}] [h=frac{2}{b}sqrt{pleft(p-aright)left(p-bright)left(p-cright)}]

По теореме 1, получим

[S=frac{1}{2}bh=frac{b}{2}cdot frac{2}{b}sqrt{pleft(p-aright)left(p-bright)left(p-cright)}=sqrt{pleft(p-aright)left(p-bright)left(p-cright)}]

Теорема доказана.

«Формула Герона» 👇

Примеры задач на использование формулы Герона

Пример 1

Найти площадь треугольника, если его стороны равняются $3$ см, $6$ см и $7$ см.

Решение.

Найдем вначале полупериметр этого треугольника

[p=frac{3+6+7}{2}=frac{16}{2}=8 см]

По теореме 2, получим

[S=sqrt{8left(8-3right)left(8-6right)left(8-7right)}=sqrt{8cdot 5cdot 2cdot 1}=4sqrt{5}]

Ответ: $4sqrt{5}$.

Пример 2

Найти площадь параллелепипеда, со сторонами $8$ см и $5$ см и меньшей диагональю, равной $5$ см.

Решение.

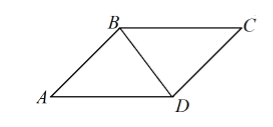
Пусть нам дан параллелограмм $ABCD$, где $AD=8 см, AB=5 см и BD=5 см$ (рис. 2).

Рисунок 2.

Так как диагональ параллелограмма является его осью симметрии, то треугольники $ABD$ и $BDC$ равны между собой. Следовательно

[S=S_{ABD}+S_{BDC}=2S_{ABD}]

Полупериметр треугольника $ABD$ равен

[p=frac{5+5+8}{2}=frac{18}{2}=9 см]

По теореме 2

[S_{ABD}=sqrt{9left(9-5right)left(9-5right)left(9-8right)}=sqrt{9cdot 4cdot 4cdot 1}=12]

Следовательно

[S=2cdot 12=24]

Ответ: $24$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник


3607	В треугольнике ABC AB=5, BC=4, AC=6. Точка D принадлежит BC. BD:DC=2:3. CK — биссектриса. CK пересекает AD в точке M, BM пересекает AC в точке O. Найти а) Площадь треугольника ABD б) Площадь треугольника BMC Решение	В треугольнике ABC AB=5, BC=4, AC=6. Точка D принадлежит BC ! Задача на теорему Чевы # Два способа решения: с применением теоремы Чевы и без неё

2317	В треугольнике ABC площадью 10,5 кв м сторона AB=10 м. Найдите отношение, в котором эта сторона делится точкой касания вписанной в треугольник окружности, если радиус этой окружности равен 1 м Решение	В треугольнике ABC площадью 10,5 кв м сторона AB=10 м ! Задача на свойство касательных и формулу Герона из вступительного экзамена в ЛГУ (1996)

2316	В треугольнике ABC площадью 42 кв см сторона AB=7 см. Найдите радиус вписанной в треугольник окружности, зная, что точка касания K делит сторону AB в отношении 1:6 Решение	В треугольнике ABC площадью 42 кв см сторона AB=7 см. Найдите радиус вписанной в треугольник окружности ! Задача на свойство касательных из вступительного экзамена в ЛГУ (1996)

1900	Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 29, а основание BC = 4. Биссектриса угла ADC проходит через середину AB. Найдите площадь трапеции ABCD Решение	Боковые стороны AB и CD трапеции ABCD равны соответственно ! 10 вариантов математика ОГЭ 2020 Типовые варианты экзаменационных заданий Ященко Вариант 6 Задание 26 # Задача — Аналог 298

1897	Найдите площадь трапеции, диагонали которой равны 16 и 12, а средняя линия равна 10 Решение	10 вариантов математика ОГЭ 2020 Типовые варианты экзаменационных заданий Ященко Вариант 1 Задание 26 # формула Герона # Задачи-Аналог 1387 1278

1387	Найдите площадь трапеции, диагонали которой равны 17 и 9, а средняя линия равна 5 Решение	38 вариантов математика ОГЭ 2020 Типовые варианты экзаменационных заданий Ященко Вариант 24, Вариант 27 Задание 26 ! 50 вариантов математика ОГЭ 2019 Высоцкий Ященко Вариант 4 Задача 26 # формула Герона # Задачи-Аналоги 1897 1278

1278	Найдите площадь трапеции, диагонали которой равны 15 и 13, а средняя линия равна 7 Решение	38 вариантов математика ОГЭ 2020 Типовые варианты экзаменационных заданий Ященко Вариант 35 Задание 26 ! 38 вариантов математика ОГЭ 2019 Высоцкий Ященко Вариант 1 Задача 26# формула Герона # Задачи-Аналоги 1897 1387

1254	В трапеции ABCD основания AD и BC равны 25 см и 4 см, а боковые стороны AB и CD — 20 см и 13 см соответственно. Найдите высоту трапеции. Найдите ответ с точностью до целого числа Решение	Всероссийская контрольная «Выходи решать» Пробный тур! Решения задач по математике

298	Боковые стороны AB и CD трапеции ABCD 12 и 13, а основание BC = 4. Биссектриса угла ADC проходит через середину AB. Найти площадь трапеции ABCD Решение	38 вариантов математика ОГЭ 2020 Типовые варианты экзаменационных заданий Ященко Вариант 7 Задание 26 ! математика 36 вариантов ФИПИ Ященко ОГЭ 2018 Типовые экзаменационные варианты — Вариант 27 Задание 26 # Ященко ОГЭ 2016 вариант 15 (16) # Задача — Аналог 1900