Тип 2 № 8852
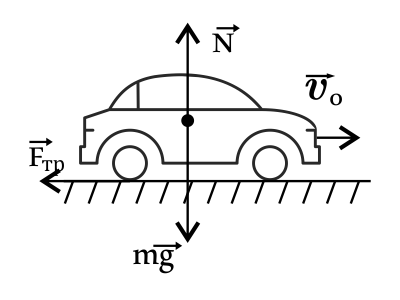
К бруску массой m1 = 3 кг, находящемуся на закреплённой наклонной шероховатой плоскости, приложена сила F = 12 Н, направленная вдоль плоскости, как показано на рисунке. При этом брусок движется вверх с ускорением. На какую величину изменится ускорение бруска, если, не изменяя модуля и направления силы
заменить брусок на другой — из того же материала, но массой
? Ответ выразите в метрах на секунду в квадрате.
Решение.
Запишем второй закон Ньютона в векторной форме:
Спроецируем на ось, вдоль которой движется тело (Ox), и на ось, перпендикулярную ей (Oy):
где — угол наклона плоскости,
— коэффициент трения.
После замены бруска это уравнение будет выглядеть следующим образом:
Для того чтобы избавиться от неизвестных величин, поделим первое уравнение на второе:
Ответ: 2.
Задания Д B18 № 8852
К источнику постоянного тока подсоединили две лампы (см. рис.), имеющие одинаковые электрические сопротивления. Чему равна мощность электрического тока, потребляемая каждой лампой, если показания идеального амперметра и вольтметра равны соответственно 3 А и 6 В ?
Спрятать решение
Решение.
Лампы соединены параллельно. Вычислим общее сопротивление участка цепи, на котором расположены обе лампы:
где R — общее сопротивление участка цепи, на котором расположены обе лампы, включённые в цепь, изображённую на рисунке, r — сопротивление лампы.
Из закона Ома находим, что R = 6 В/3 А = 2 Ом. Следовательно, сопротивление лампы равно 4 Ом. Мощность лампы:
Ответ: 9.
Условие:
Две частицы, отношение масс которых, m1/m2=2 отношение зарядов q1/q2=1/2 , попадают в од-Две частицы, отношение масс которых, m1/m2=2 отношение зарядов q1/q2=1/2 , попадают в однородное магнитное поле, вектор магнитной индукции которого перпендикулярен векторам скорости частиц. Кинетические энергии частиц одинаковые. Чему равно отношение радиусов кривизны траекторий R1/R2 первой и второй частиц в магнитном поле?
Решение:
Частицы отношение масс которых равно двум отношение зарядов равно 1/2 попадают в однородное магнитное поле вектор магнитной индукции которого перпендикулярен векторам скорости частиц кинетическая энергия частиц одинакова и Чему равно отношение радиусов кривизны 1 2 частицы в магнитном поле вспоминаем так как частицы движется в магнитном поле и его скорость их скорость перпендикулярно вектору магнитной индукции то данной частицы движутся по окружности а следовательно на них действует сила Лоренца который уравновешивает уравновешивается центростремительной силой сила Лоренца равна qvb центростремительная сила равна M а центростремительное центростремительное ускорение равно в квадрат деленное на Р объединяет данные формулы получают qvb будет равно n в квадрат деленное на Р отсюда скорость будет равна qbr / намаз второй этап у нас в условии задачи сказано что кинетической энергии частиц одинаковой такое кинетическая энергия одинаковые вспоминаем Что такое кинетическая энергия это произведение массы на его скорость квадрате деленное на 2 записываем для второй части cm2 в 2 в квадрате деленное на 2 приравнивает правой части получаем M1 V1 квадрате равно m2 V2 в квадрате отсюда следует что V1 к V2 всё в квадрате будет равно отношение масс m2 M1 то есть V1 к V2 будет равно корню квадратному из m2 M1 радиус траектории частицы будет равен ымв Зелёная на куб Нам необходимо найти отношение радиуса R1 R2 масса у нас разная поэтому записью и M1 m2 скорости у нас зависят от мас V1 к V2 заряды у нас также разные Q1 Q2 А вот магнитное поле у нас одинаково поэтому мы данной множитель не записывая подставляя значения вместо V1 к V2 мы получаем М 12 / m2 Coupe de и умножить на корень квадратный из и m2 M1 упрощаем данное выражение получаем корень квадратный из млн км2 умножить на 2 на К1 подставляя значения мы получаем корень из 2 х 2 корень из 2 Это примерно 1,4 надо бы получаем 2,8 и так ответ отношение радиусов примерно равно 2/8
Источник: ЕГЭ-2020 Физика (20 экзаменационных вариантов) «Экзаменационный тренажер к новой официальной экзаменационной версии ЕГЭ». С.Б. Бобошина
Разбор решения. (Видео)
Силы в природе, законы Ньютона. Закон всемирного тяготения, закон Гука, сила трения
В. З. Шапиро
Второе задание ЕГЭ по физике проверяет знания по разделу «Динамика». Это задание базового уровня сложности, без возможности выбора ответа. Для его решения необходимо знать законы Ньютона, формулы, которые выражают силу тяжести, силу всемирного тяготения, силу упругости, вес тела, силу трения, силу реакции опоры на горизонтальной поверхности и на наклонной плоскости. Во многих задачах применяется одна и та же формула, но в различных ситуациях. Как правило, необходимо составить и решить систему из двух уравнений.
Применение закона всемирного тяготения
Необходимая теория: Сила тяготения
1. Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Во сколько раз больше будет модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами в два раза больше, а массы звёзд равны 2m и 3m?
Ответ: в _________________________ раз(а).
В этой задаче необходимо записать формулу закона всемирного тяготения для двух случаев:
(1).
(2).
Разделив (2) на (1), получим:
Ответ: в 1,5 раза.
Подобные задачи проверяют знания основных физических формул. Их необходимо записать в общем виде и в случае, когда происходит изменение какой-либо физической величины. Полученную систему уравнений решаем любым удобным способом. Задания такого типа часто встречаются в различных разделах курса физики.
Применение II закона Ньютона
Необходимая теория: Второй и третий законы Ньютона
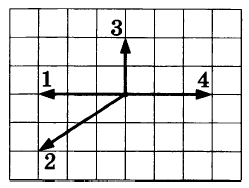
2. На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Сторона клетки соответствует 1 Н. Определите модуль равнодействующей сил, приложенных к телу.
Равнодействующая сила равна геометрической сумме сил, приложенных к телу.
Следующий шаг – найти сумму проекций сил на оси OX и OY.
Сумма проекций сил на ось OX равна:
Сумма проекций сил на вертикальную ось равна:
По теореме Пифагора, модуль равнодействующей силы определяется:
Ответ: 2 Н.
Секрет решения: Многие задачи по динамике требует прочных знаний по геометрии. Теорема Пифагора, а также соотношения в прямоугольном треугольнике являются обязательными инструментами для тех, кто собирается сдавать экзамен по физике.
Применение формулы силы упругости (закон Гука)
Необходимая теория: Сила упругости
3. Подвешенная к потолку пружина под действием силы 5 Н удлинилась на 10 см. Чему равно удлинение этой пружины под действием силы 8 Н?
Ответ: ___________________________ см.
Запишем формулу закона Гука для двух случаев:
(1)
(2)
Разделим (2) на (1).
(м).
Ответ: 16 см.
Задача решается стандартным применением физической формулы для двух случаев. Обратите внимание на единицы измерения, которые требуются в ответе.
Применение формул для силы реакции опоры и силы трения
Необходимая теория: Сила трения
4. Тело движется по горизонтальной плоскости. Нормальная составляющая силы воздействия тела на плоскость равна 40 Н, сила трения равна 10 Н. Определите коэффициент трения скольжения.
Ответ: ___________________________.
Общая формула для силы трения имеет вид:
где N — сила реакции опоры.
Отсюда коэффициент трения можно выразить
Проведем расчет:
Ответ: 0,25.
Секрет решения: Помним, что коэффициент трения находится в интервале от 0 до 1. Это поможет вам более уверенно решать задачи на расчет коэффициента трения.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 2 ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Задание №2 ЕГЭ по физике охватывает большое количество тем механики, поэтому рекомендуется прорешать прилагаемую подборку, чтобы быть готовым к заданию любого типа.
В сборнике 60 задач с ответами.
→ Скачать сборник — ege-fizika-zadanie-2
Автор: Суслов Андрей Антонович — преподаватель физики.
Статья по этой теме: vk.com/@postypashki
Темы, которые могут встретиться в этом задании
→ непосредственное применение второго закона Ньютона;
→ сложение силы и вычисление модуля равнодействующей силы;
→ второй закон Ньютона в импульсной формулировке;
→ вес тела при движении с ускорением;
→ сила упругости и закон Гука;
→ сила трения покоя и сила трения скольжения, закон Кулона-Амонтона;
→ движение по гладкой наклонной плоскости и движение по наклонной плоскости с трением;
→закон Всемирного тяготения, движение искусственных спутников по круговым орбитам.
Советы по выполнению задания
— Будьте внимательны при вычислении проекций векторов сил и ускорений, особенно в задачах о наклонной плоскости. Традиционные ошибки: перепутали синус и косинус; забыли, что проекция отрицательна и т. д.
— Иногда в задачах требуется округлить полученный ответ. Если получается несократимая дробь, но в условии про округление ничего не сказано, значит вы получили неправильный ответ. Пересчитайте заново.
— На выполнение этого задания должно уходить в среднем 3 минуты. Не спешите, прочтите условие внимательно, вспомните формулы, аккуратно сделайте на черновике всё расчёты. Но и очень долго размышлять тоже не стоит. Это одно из самых простых заданий, и тратить на него много времени нельзя.
Смотрите также:
В результате выполнения задания 2 ЕГЭ по физике проверяются следующие требования/умения:
Коды проверяемых требований к уровню подготовки (по кодификатору):
Читать подробнее…
Коды проверяемых элементов содержания (по кодификатору):
Уровень сложности задания:
Максимальный балл за выполнение задания:
Примерное время выполнения задания выпускником, изучавшим предмет:
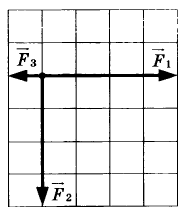
На рисунке представлены три вектора сил, приложенных к одной точке и лежащих в одной плоскости. Модуль вектора силы F1 равен 4 Н. Чему равен модуль равнодействующей векторов F1, F2, F3?
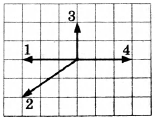
На рисунке представлены четыре вектора сил, действующих на тело. С исключением какой из четырёх сил ускорение тела будет равно нулю? В ответе укажите номер вектора этой силы.
Пружина жесткости k = 104 Н/м одним концом прикреплена к неподвижной опоре, а к другому ее концу приложили силу F = 1000 Н. Определите растяжение пружины.
Лифт движется вверх с ускорением 2 м/с2, в нем находится пассажир массой 50 кг. Чему равен модуль силы тяжести, действующей на пассажира?
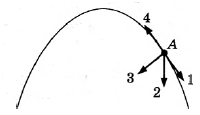
На рисунке показана траектория движения тела, брошенного под некоторым углом к горизонтальной поверхности Земли. В точке А этой траектории направление вектора скорости обозначено стрелкой 1; траектория движения тела и все векторы лежат в плоскости, перпендикулярной поверхности Земли. Сопротивление воздуха пренебрежимо мало. Какое направление имеет вектор ускорения
тела в системе отсчёта Земля? В ответе укажите номер соответствующей стрелки.
В инерциальной системе отсчета сила $$oversetrightharpoonup F$$ сообщает телу массой m ускорение, равное по модулю 8 м/с2. Чему равен модуль ускорения тела массой 2m под действием силы $$frac{oversetrightharpoonup F}2$$ в этой системе отсчета?
На рисунке представлены четыре вектора сил, действующих на тело. С исключением какой из четырёх сил ускорение тела будет равно нулю? В ответе укажите номер вектора этой силы.
Под действием одной силы $$vec{F_1}$$ тело движется с ускорением 4 м/с2. Под действием другой силы $$vec{F_2}$$, направленной противоположно силе $$vec{F_1}$$, ускорение тела равно 3 м/с2. С каким ускорением будет двигаться тело при одновременном действии сил $$vec{F_1}$$ и $$vec{F_2}$$ ?
В инерциальной системе отсчета сила $$oversetrightharpoonup F$$ сообщает телу массой m ускорение, равное по модулю 2 м/с2. Чему равен модуль ускорения тела массой $$frac m2$$ под действием силы 2$$oversetrightharpoonup F$$ в этой системе отсчета?
Среднее расстояние между центрами Луны и Земли примерно 60 земных радиусов. Во сколько раз уменьшится сила гравитационного взаимодействия предмета массой 1 кг и Земли, если сначала предмет находится на поверхности Земли, а затем на лунной орбите?
Ответ: в____________раз
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 76.3%
Ответом к заданию 2 по физике может быть целое число или конечная десятичная дробь.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
Автомобиль массой 4 т движется со скоростью 36 км/ч. Какой путь прошёл автомобиль до полной остановки, если коэффициент трения колёс о дорогу равен 0,3? Движение считать равнозамедленным. Ответ выразите в (м). Ответ округлите до десятых
Решение
Дано:
$m=4000$кг
$μ=0.03$
$g=10м/с^2$
$υ_0=36=10$м/с
$υ_к=0$
$А-?$
Решение:
Работа силы трения равна: $A_{F_{тр}}=∆E_к$(1), где $A_{F_{тр}}=F_{тр}·S=μNS=μmgS$(2), где $S$ — путь автомобиля до полной остановки. $∆E_к={mυ_к^2}/{2}-{mυ_0^2}/{2}=-{mυ_0^2}/{2}$(3). Знак «минус» опустим так как он говорит, что сила трения направлена в сторону, противоположную движению, тогда имеем: $μmgS={mυ_0^2}/{2}⇒S={υ_0^2}/{2μg}={100}/{6}=16.66=16.7$м.
Ответ: 16.7
Задача 2
Пружину, жёсткость которой равна 1 · 104 Н/м, сжали с силой 400 Н. Вычислите потенциальную энергию, запасённую пружиной. Ответ выразите в (Дж).
Решение
Дано:
$k=10^4$Н/м
$F=400$Н
$E_{п}-?$
Решение:
Запишем закон Гука: $F=kx$(1), где $x$ — удлинение (в нашем случае, сжатие) пружины, $k$ — жесткость пружины. Откуда: $x={F}/{k}={400}/{10^4}=0.04$м(2).
Потенциальная энергия сжатой пружины определяется выражением: $E_{п}={kx^2}/{2}={10^4·16·10^{-4}}/{2}=8$Дж.
Ответ: 8
Задача 3
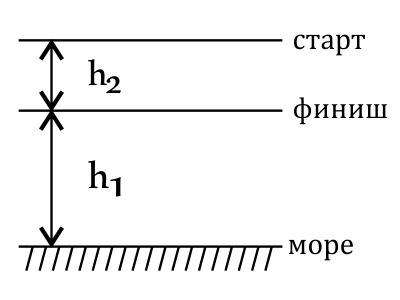
Точка финиша трассы горнолыжных соревнований находится на высоте 2 км над уровнем моря, а точка старта — на высоте 400 м над точкой финиша. Чему равна потенциальная энергия лыжника на старте относительно уровня моря? Масса лыжника 70 кг. Ответ выразите в (МДж).
Решение
Дано:
$m=70$кг
$g=10м/с^2$
$h_1=2000$м
$h_2=400$м
$E_{п}-?$
Решение:
Потенциальная энергия лыжника на старте относительно уровня моря по определению равна: $E_{п}=mg(h_1+h_2)=70·10·(2000+400)=700·2400=1680000=1.68$МДж.
Ответ: 1.68
Задача 4
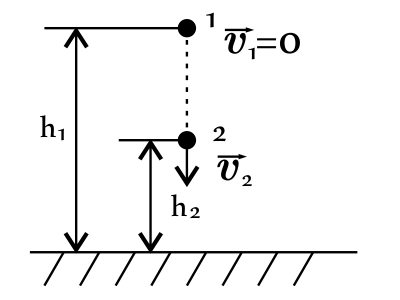
Тело массой 2 кг начинает свободно падать с высоты 5 м. Чему равна кинетическая энергия тела на высоте 2 м от земли? Ответ выразите в (Дж).
Решение
Дано:
$m=2$кг
$g=10м/с^2$
$h_1=5$м
$h_2=2$м
$E_{к_2}-?$
Решение:
Полная механическая энергия тела в точке 1 равна полной механической энергии тела в точке 2: $E_1=E_2$(1), где $E_1=E_{п_1}+E_{к_1}=mgh_1+{mυ_1^2}/{2}=mgh_1$(2), $E_2=E_{п_2}+E_{к_2}=mgh_2+E_{к_2}$(3).
Подставим (2) и (3) в (1) и найдем $E_{к_2}:mgh_1=mgh_2+E_{к_2}$, откуда $E_{к_2}=mg(h_1-h_2)$(4).
Подставим числовые значения в (4), получим: $E_{к_2}=2·10·(5-2)=60$Дж.
Ответ: 60
Задача 5
Материальная точка массой 4,6 кг равномерно движется по окружности. Чему равна её скорость, если изменение её импульса за два с половиной периода составило 18,4 кг·м/с? Ответ выразить в (м/с).
Решение
Дано:
$m=4.6$кг
$t=2.5T$
$Δp↖{→}=18.4кгм/с$
$υ-?$
Решение:
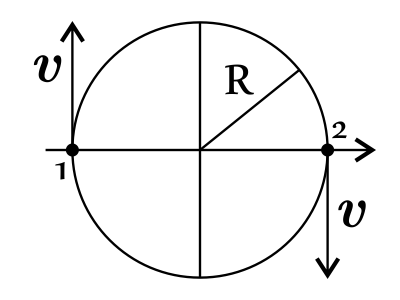
Исходя из рисунка $p_1$ и $p_2$ противонаправлены, тогда: $υ={Δp↖{→}}/{2·m}={18.4}/{2·4.6}=2м/с$
Ответ: 2
Задача 6
Падение тела массой 2 кг с некоторой высоты занимает 10 с. Найдите кинетическую энергию, которой будет обладать тело при падении на землю. Ответ выразите в (кДж).
Решение
Дано:
$m=2$кг
$t=10$с
$E_к-?$
Решение:
1) $E_к=E_n=mgh$ по закону сохранения
2) $S=H={gt^2}/{2}={10·100}/{2}=500$м
$E_n=mgh=2·10·500=10$кДж
Ответ: 10
Задача 7
Тело подбросили вертикально вверх с начальной скоростью 6 м/с. На какой высоте кинетическая энергия тела будет в два раза больше его потенциальной энергии? Ответ выразите в (м).
Решение
Дано:
$υ_0=6$м/с
$E_к=2·E_n$
$h-?$
Решение:
${table.{mυ_0^2}/{2}=E’_к+E’_n; .{E_к}/{2}=E_n;$
$⇒{mυ_0^2}/{2}=3E_n⇒{υ_0^2}/{2}=3gh$.
$h={υ_0^2}/{2g·3}={36}/{60}=0.6$м
Ответ: 0.6
Задача 8
На покоящуюся тележку массой 0,2 т налетает тележка массой 0,3 т со скоростью 8 км/ч . Найдите скорость, с которой эти тележки начали двигаться совместно после удара. Ответ выразите в (км/ч).
Решение
Дано:
$m_1=200$кг
$m_2=300$кг
$υ_1=8{км}/ч$
$υ_2-?$
Решение:
По закону сохранения энергии $m_1·0+m_2·υ_1=(m_1+m_2)υ_2$ выразим: $υ_2={m_2·υ_1}/{m_1+m_2}={300·8}/{200+300}=4.8{км}/ч$
Ответ: 4.8
Задача 9
Найдите, чему равно отношение масс большего тела к меньшему, если до абсолютного неупругого столкновения они двигались навстречу друг другу со скоростями 10 м/с каждое, а после — со скоростью 5 м/с.
Решение
Дано:
$υ_1=10м/с$
$υ_2=5м/с$
${M}/{m}-?$
Решение:
Запишем закон сохранения импульсов: $M·υ_1-m·υ_1=(M+m)υ_2$.
$10·M-10·m=5M+5m$
$5M=15m; {M}/{m}={15}/{5}=3$
Ответ: 3
Задача 10
Санки массой 50 кг из состояния покоя съезжают с гладкой наклонной плоскости высотой 5 м. После этого они продолжают двигаться по горизонтальной поверхности и спустя некоторое время останавливаются. Как при этом изменилась их механическая энергия? В ответе запишите: уменьшилась на _ (кДж).
Решение
Дано:
$m=50$кг
$h=5$м
$∆E_m-?$
$m_0=1·10^{-6}$кг
Решение:
По закону сохранения $∆E_m=∆E_h+∆E_к; ∆E_к=0$
$∆E_r=mgh=50·5·10=2.5$кДж. Тогда $∆E_{мех}=∆E_n=2.5$кДж.
Ответ: 2.5
Задача 11
Тела 1 и 2 взаимодействуют только друг с другом. Изменение кинетической энергии тела 1 за некоторый промежуток времени равно 15 Дж. Работа, которую совершили за этот же промежуток времени силы взаимодействия тел 1 и 2, равна 45 Дж. Чему равно изменение кинетической энергии тела 2 за это время? Ответ выразить в (Дж).
Решение
Дано:
$∆E_1=15$Дж
$∆E_в=45$Дж
$∆E_2-?$
Решение:
По закону сохранения энергии запишем уравнение взаимодействия: $∆E_1+∆E_2=∆E_в⇒∆E_2=∆E_в-∆E_1$
$∆E_2=45-15=30$Дж
Ответ: 30
Задача 12
Мальчик столкнул санки массой 2 кг с вершины горки. Сразу после толчка санки имели скорость 4 м/с, а у подножия горки она равнялась 8 м/с. Трение санок о снег пренебрежимо мало. Какова высота горки? Ответ выразите в (м).
Решение
Дано:
$υ_0=4$м/с
$υ_к=8$м/с
$F_{тр}=0$
$H-?$
Решение:
Запишем закон сохранения энергии для данного случая $E_{к_0}+E_п=E_к^к$. $E_{к_0}$ — кинетическая энергия в начальный момент; $E_п$ — потенциальная энергия в начальный момент; $E_к^к$ — кинетическая энергия в конце пути.
$E_п=E_к^к-E_{к_0}$
$mgH={m·υ_к^2}/{2}-{m·υ_0^2}/{2}$
$2·10·H=64-16⇒H=2.4$м
Ответ: 2.4
Задача 13
Легковой автомобиль и грузовик движутся со скоростями 108 км/ч и 72 км/ч соответственно. Масса грузовика 4500 кг. Какова масса легкового автомобиля, если импульс грузовика больше импульса легкового автомобиля в 2 раза? Ответ выразите в (кг).
Решение
Дано:
$υ_л=108$км/ч$=30м/с$
$υ_г=72$км/ч$=20м/с$
$m_г=4500кг$
$p_г=2p_л$
$m_л-?$
Решение:
По определению импульс тела равен: $p=mυ$(1), тогда $p_г=m_г·υ_г$(2) — импульс грузового автомобиля; $p_л=m_л·υ_л$(2) — импульс легкового автомобиля. По условию задачи: $p_г=2p_л$(4). Подставим (2) и (3) в (4): $m_г·υ_г=2m_лυ_л⇒m_л={m_г·υ_г}/{2υ_л}$(5). Подставим числовые значения в (5): $m_л={4500·20}/{30·2}=1500кг$.
Ответ: 1500
Задача 14
Автомобиль массой 1 т двигался со скоростью 72 км/ч. Максимальное значение коэффициента трения шин о дорожное покрытие равно 0,7. Каков минимальный тормозной путь автомобиля? Ответ округлите до целых. Ответ выразите в (м).
Решение
Дано:
$m=1000$кг
$υ=72км/ч=20м/с$
$g≈10м/c^2$
$μ_{max}=0.7$
$S_{min}-?$
Решение:
Работа силы трения равна изменению кинетической энергии автомобиля: $A_{F_{тр}}=∆E_к$(1), где $A_{F_{тр}}=F_{тр}·S_{min}·cos180°$(2). $∆E_к=0-{mυ^2}/{2}=-{mυ^2}/{2}$(3), т.к. автомобиль останавливается; $cos180°=-1$
$F_{тр}=μ_{max}·N=μ_{max}·mg$(4).
Подствим (2), (3), (4) в выражение (1): $-μ_{max}·mg·S_{min}=-{mυ^2}/{2}⇒S_{min}={υ^2}/{2μ_{max}·g}$(5)
$S_{min}={400}/{2·0.7·10}=28.57м=29м$
Ответ: 29
Задача 15
Ученик исследовал зависимость силы упругости F пружины от её растяжения x и получил следующие результаты:
| F, H | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 |
| x, см | 0 | 2 | 4 | 6 | 8 | 10 |
По данным опыта определите, какую работу нужно совершить, чтобы растянуть пружину от 4 см до 8 см. Ответ выразите в (Дж).
Решение
Дано:
$x_1=4см=4·10^{-2}м$
$x_2=8см=8·10^{-2}м$
$A-?$
Решение:
Работа силы упругости пружины равна убыли ее потенциальной энергии: $A={kx_1^2}/{2}-{kx_2^2}/{2}$(1), где $k$ — жесткость пружины.
Найдем жесткость пружины $k$. Для этого возьмем любые значения силы упругости пружины и растяжения, отличные от нуля, например, $F_{тр}=1H, x=0.04м$. Тогда, по закону Гука имеем: $F_{упр}=kx⇒k={F_{упр}}/{х}$(2). $k={1}/{0.04}=25Н/м$
Подставим числовые значения в (1) и найдем работу $A$: $A={25}/{2}((4·10^{-2})^2-(8·10^{-2})^2)=12.5·(16·10^{-4}-64·10^{-4})=-600·10^{-4}=-0.06$Дж.
Зная, что «минус» говорит о том, что при растяжении сила упругости направлена противоположно растяжению пружины.
Ответ: 0.06
Задача 16
Шарик массой 100 г налетает со скоростью 2 м/с на покоящийся шар такой же массы. Каков импульс системы шаров после абсолютно неупругого удара? Ответ выразите в (кг·м/с).
Решение
Дано:
$m_1=m_2=m=0.1кг$
$υ_1=2{м}/{с}; υ_2=0{м}/{с}$
$p-?$
Решение:
По закону сохранения импульса: импульс системы до взаимодействия равен импульсу системы после взаимодействия: $p=p_1+p_2=m_1·υ_1+m_2·υ_2=m_1υ_1=0.1·2=0.2{кг·м}/{с}$
Ответ: 0.2
Задача 17
Кинетическая энергия равномерно движущегося тела массой 200 г равна 10 Дж. С какой скоростью движется тело? Ответ выразите в (м/с).
Решение
Дано:
$m=200г=0.2кг$
$Е_к=10Дж$
$υ-?$
Решение:
Кинетическая энергия определяется выражением:$Е_к={mυ^2}/{2}$(1), откуда выразим скорость $υ: $.
Учитывая, что $mυ^2=2Е_к$, $υ^2={2E_к}/{m}$, $υ=√{{2E_к}/{m}}$(2).
Подставим числовые значения в (2): $υ^2=√{{2·10}/{0.2}}=√{100}=10{м}/{с}$
Ответ: 10
Задача 18
Тело массой 200 г, двигаясь равномерно, обладает импульсом 4 кг·м/с. Какова его кинетическая энергия? Ответ выразите в (Дж).
Решение
Дано:
$m=200г=0.2кг$
$p=4{кг·м}/{с}$
$Е_к-?$
Решение:
Импульс по определению равен: $p=mυ$(1), а кинетическая энергия определяется выражением:$Е_к={mυ^2}/{2}$(2).
Учитывая, что $mυ^2={m^2υ^2}/{m}={(mυ)^2}/{m}={p^2}/{m}$(3), подставим (3) в (2): $Е_к={p^2}/{2m}$(4).
Подставим числовые значения в (4): $Е_к={4^2}/{2·0.2}={16}/{0.4}=40$Дж
Ответ: 40