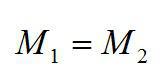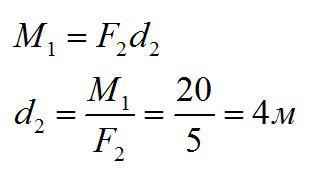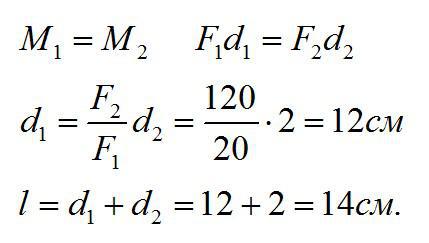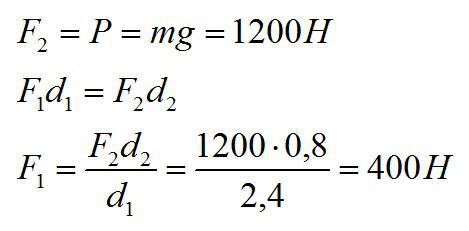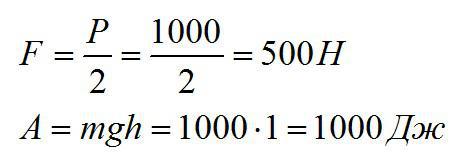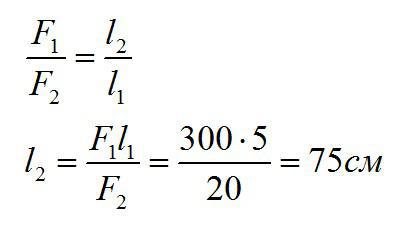Егэ физика задачи на момент силы - Помощь в подготовке к экзаменам и поступлению

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 544 1–20 | 21–40 | 41–60 | 61–80 | 81–100 | 101–120 …

Добавить в вариант

Два небольших шара массами m₁ = 0,2 кг и m₂ = 0,3 кг закреплены на концах невесомого стержня AB, расположенного горизонтально на опорах C и D (см. рис.). Расстояние между опорами l = 0,6 м, а расстояние AC равно 0,2 м. Чему равна длина стержня L, если сила давления стержня на опору D в 2 раза больше, чем на опору C? Сделайте рисунок с указанием внешних сил, действующих на систему тел «стержень  — шары».

Какие законы Вы используете для описания равновесия тела? Обоснуйте их применение к данному случаю.

Источник: Демонстрационная версия ЕГЭ—2020 по физике.

Однородная лестница массой 20 кг прислонена к гладкой вертикальной стене, составляя с ней угол 60^о. Пол шероховатый. Чему равен модуль силы реакции, действующей на верхний конец лестницы? Ответ дайте в ньютонах и округлите до целого числа.

Однородная лестница массой 20 кг прислонена к гладкой вертикальной стене, составляя с ней угол 30^о. Пол шероховатый. Чему равен модуль силы реакции, действующей на верхний конец лестницы? Ответ дайте в ньютонах, округлите до целого числа.

К горизонтальной лёгкой рейке, лежащей на двух опорах А и В, в точке О прикреплён груз массой 10 кг. Длина отрезка ОА равна 4 м, длина отрезка ОВ равна 1 м. Определите модуль силы, с которой действует на рейку опора В.

К лёгкой рейке подвешено на нити тело массой 7 кг (см. рис.). Рейка уравновешена на шероховатой опоре в горизонтальном положении с помощью силы vecF, приложенной к концу рейки и направленной под углом α = 30° к горизонту. Определите модуль вертикальной составляющей силы реакции опоры, действующей на рейку в точке O.

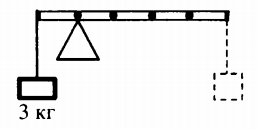
На рисунке изображен невесомый стержень длиной 3 м, расположенный в стакане под углом 45°. На расстоянии 1 м от нижнего угла подвешен шарик массой 3 кг. Найдите силу, с которой стержень давит на стенку стакана.

Источник: ЕГЭ по физике 13.07.2020. Основная волна. ЦФО. Часть C. Вариант 2

Задания Д29 C2 № 4367

На зиму в подмосковном яхт-клубе катера и яхты вытаскивают на берег по бетонному «слипу», то есть наклонной плоскости, уходящей под воду. Под плавающее судно помещают под водой лёгкую тележку, которая практически без трения может кататься по слипу, и при помощи лебёдки и системы блоков вытаскивают судно, поднимая его над уровнем воды.

Найдите максимальное водоизмещение судна, которое можно медленно вытащить из воды при помощи показанной на рисунке системы простых механизмов, если лебёдка даёт выигрыш в силе в n=5 раз, к её ручке прикладывают максимальную силу f=250H, а угол наклона слипа к горизонту равен рад. Трением можно пренебречь.

Примечания: водоизмещением называется масса воды, вытесняемой судном (измеряется обычно в тоннах); при углах рад можно считать

Источник: Демонстрационная версия ЕГЭ—2022 по физике

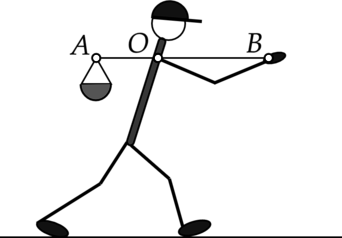
Человек несёт груз на лёгкой палке (см. рис.). Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA? Ответ дайте в сантиметрах.

Источник: Демонстрационная версия ЕГЭ—2020 по физике.

К левому концу невесомого стержня прикреплен груз массой 3 кг (см. рис.).

Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии? (Ответ дайте в килограммах.)

Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рис.).

Чему равна масса груза, который надо подвесить ко второму делению левого плеча рычага для достижения равновесия? (Ответ дайте в килограммах.)

Велосипедное колесо, у которого вместо металлических спиц обод удерживают натянутые резинки, установлено в вертикальной плоскости и может свободно вращаться вокруг своей горизонтальной оси, зажатой в штативе. К неподвижному колесу подносят слева мощную лампу и начинают нагревать резиновые «спицы» (см. рис.). Резина, в отличие от металла, при нагревании не расширяется, а сжимается. Опишите, опираясь на известные физические законы, что будет происходить с резинками, и как колесо будет двигаться.

Ступенчатый блок имеет внутренний шкив радиусом 6 см. К нитям, намотанным на внешний и внутренний шкивы, подвешены грузы так, как показано на рисунке. Трение в оси блока отсутствует. Чему равен радиус внешнего шкива блока, если система находится в равновесии? Ответ выразите в сантиметрах.

Источник: ЕГЭ по физике 11.06.2021. Основная волна. Разные задания

Тело массой 0,3 кг подвешено к правому плечу невесомого рычага (см. рис.). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия? Ответ приведите в килограммах.

Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рис.). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

Источник: Демонстрационная версия ЕГЭ—2018 по физике

В постоянном однородном магнитном поле с индукцией B = 0,2 Тл находится прямоугольная проволочная рамка, сделанная из проволоки длиной 8 см, по которой пропускают ток силой I = 20 мА. Какое максимальное значение может иметь действующий на эту рамку момент сил Ампера?

Многовитковая катушка гальванометра намотана тонким проводом на плоский прямоугольный каркас с размерами a  =  2 см и b  =  3 см и подвешена на проводах в однородном горизонтальном магнитном поле с индукцией B  =  0,05 Тл так, что более длинная сторона катушки вертикальна, а её плоскость составляет угол с вектором vec B. Когда по катушке пустили ток I  =  200 нА, на неё стал действовать момент сил M  =  1,2 · 10 − 9 Н · м. Каково число N витков провода в катушке?

В некоторый момент времени скорость vec v электрона движущегося в магнитном поле, направлена вдоль оси х (см. рис.). Как направлен вектор магнитной индукции vecB, если в этот момент сила Лоренца, действующая на электрон, направлена вдоль оси у?

1)  из плоскости чертежа от нас otimes

2)  в отрицательном направлении оси х

3)  в положительном направлении оси х

4)  из плоскости чертежа к нам odot

Всего: 544 1–20 | 21–40 | 41–60 | 61–80 | 81–100 | 101–120 …

Источник

Задачи на простые механизмы с решениями

Формулы, используемые на уроках «Задачи на простые механизмы,
условия равновесия рычага, блоки, золотое правило механики».

Название величины	Обозначение	Единица измерения	Формула
*Сила*	F	Н	*F₁l₁ = F₂l₂*
*Плечо силы*	l	м
*Момент силы*	M	Нм	M = Fl

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
С помощью рычага рабочий поднимает плиту массой 120 кг. Какую силу он прикладывает к большему плечу рычага, равному 2,4 м, если меньшее плечо 0,8 м?

Задача № 2.
На концах рычага действуют силы 20 Н и 120 Н. Расстояние от точки опоры до большей силы равно 2 см. Определите длину рычага, если рычаг находится в равновесии.

Задача № 3.
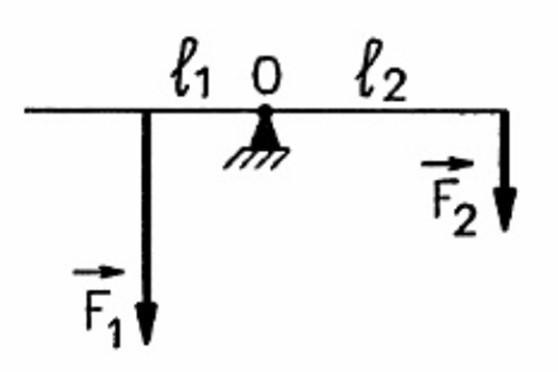
На рисунке изображен рычаг, имеющий ось вращения в точке О. Груз какой массы надо подвесить в точке В для того, чтобы рычаг был в равновесии?

Задача № 4.
На меньшее плечо рычага действует сила 300 Н, на большее — 20 Н. Длина меньшего плеча 5 см. Определите длину большего плеча.

Задача № 5.
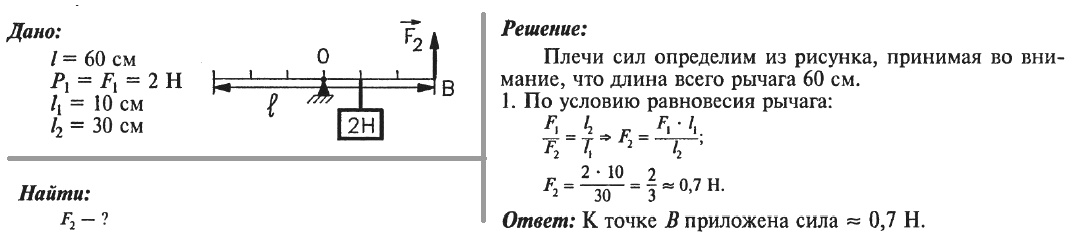
Рычаг длиной 60 см находится в равновесии. Какая сила приложена в точке В?

Задача № 6.
Момент силы действующей на рычаг, равен 20 Н*м. Найти плечо силы 5 Н, если рычаг находится в равновесии.

Задача № 7.
Какое усилие необходимо приложить, чтобы поднять груз 1000 Н с помощью подвижного блока? Какая совершится работа при подъеме груза на 1 м? (Вес блока и трение не учитывать).

Задача № 8.
Система блоков находится в равновесии. Определите вес правого груза. (Вес блоков и силу трения не учитывать).

Задача № 9.
При помощи подвижного блока поднимают груз, прилагая силу 105 Н. Определите силу трения, если вес блока равен 20 Н, а вес груза 180 Н.

Задача № 10.
ОГЭ
Стержень цилиндрической формы длиной l = 40 см состоит на половину своей длины из свинца и наполовину — из железа. Найти расстояние от центра тяжести до центра симметрии стержня. Плотность свинца p₁ = 11,4 г/см³, плотность железа p₂ = 7,8 г/см³.

Решение. Центр тяжести тела (центр масс) — точка приложения силы притяжения его к земле — веса тела P. У тел, имеющих какую-либо симметрию, он совпадает с центром симметрии. Например, у однородного цилиндра центр тяжести расположен на его оси в центре цилиндра. Тело, закреплённое на оси, проходящей через его центр тяжести, находится в состоянии безразличного равновесия. Мысленно закрепим стержень AB на оси, перпендикулярной стержню и проходящей через его центр тяжести C, отстоящий от его геометрического центра O на расстояние x в сторону более тяжёлой половины стержня. Центры инерций половинок размещены на расстояниях l/4 от середины стержня.

х = (11,4–7,8)/(11,4+7,8) • 0,4/4 = 0,01875 ≈ 0,019 (м)

Ответ: 1,9 см.

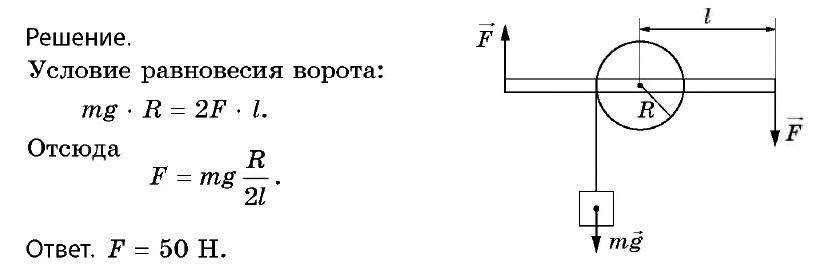
Задача № 11.
ЕГЭ
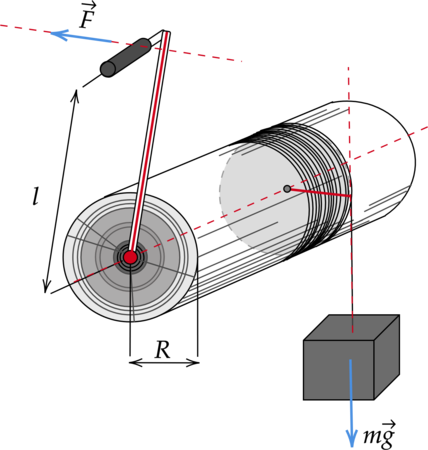
Масса якоря корабля m = 50 кг. Радиус барабана, на который наматывают якорную цепь, R = 0,2 м, длина каждой из двух ручек ворота l = 1 м. Какую силу нужно приложить к каждой из них, чтобы поднять якорь?

Краткая теория для решения задачи на простые механизмы.

Конспект урока «Задачи на простые механизмы с решениями».

Следующая тема: «Задачи на КПД простых механизмов».

Источник

4. Статика и механические колебания

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

При одновременном действии на одно тело нескольких сил тело движется с ускорением.

Линия действия силы — прямая, проходящая через вектор силы. Если силы действуют параллельно друг другу, то точки приложения результирующей силы нет.

Момент силы относительно оси вращения — это произведение силы на плечо. [vec{M}=vec{F}vec{l}]

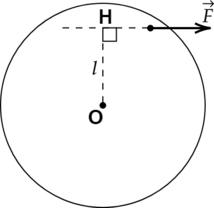
Плечо силы — это расстояние от оси вращения до линия действия силы. В качестве примера на рисунке изображён некий диск, к которому приложена сила (vec{F}). Ось вращения перпендикулярна плоскости чертежа и проходит через точку O. Плечом силы является величина (l = OH), где (displaystyle H) — основание перпендикуляра, опущенного из точки O на линию действия силы.

Момент силы считается положительным, если сила стремится поворачивать тело против часовой стрелки, и отрицательным, если по часовой стрелке.

Правило моментов

Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил равна нулю.

Условия равновесия тела:

1) Силы уравновешены вдоль любой оси.

2) Суммарный момент сил, вращающих тело в одну сторону, равен суммарному моменту сил, вращающих тело в другую сторону.

Также условия равновесия тела можно сформулировать следующим образом:

1) Равна нулю векторная сумма всех сил, приложенных к телу.

2) Равна нулю алгебраическая сумма моментов всех сил, приложенных к телу, относительно данной оси вращения или любой другой оси, параллельной данной.

Центр тяжести тела — центр параллельных сил тяжести элементарных частей этого тела.

1) Если однородное тело имеет ось симметрии, то центр тяжести находится на этой оси.

2) Если однородное тело имеет плоскость симметрии, то центр тяжести находится в этой плоскости.

3) Если однородное тело имеет центр симметрии, то центр тяжести находится в этой точке.

Виды равновесия

Равновесие называется устойчивым, если после небольших внешних воздействий тело возвращается в исходное состояние равновесия.

Равновесие называется неустойчивым, если при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия.

Равновесие называется безразличным, если при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил равна нулю.

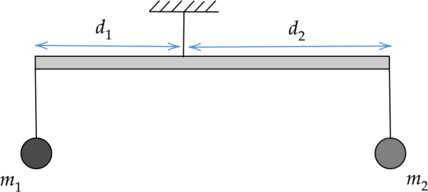
К рычагу подвешены два груза массами (m_1 = 2) кг и (m_2 = 0,5) кг так, что он находится в равновесии. Длину плеча (d_1) увеличили в 3 раза. На сколько должна измениться масса второго груза, чтобы равновесие рычага не нарушилось? (Ответ дайте в килограммах.)

Так как рычаг после увеличения длины плеча (d_1) в 3 раза остается в равновесии, то моменты сил, действующих на него справа и слева во втором случае, должны быть равны: (M_1 = M_2).
В то же время моменты сил (M_1) и (M_2) по определению равны произведению силы на ее плечо: [M_1 = F_1cdot{3d_1}] [M_2 = F_2cdot{d_2}]
Отсюда получаем: (F_1cdot{d_1} = F_2cdot{d_2})
На оба груза действует единственная сила – сила тяжести, поэтому: [F_1 = m_1g] [F_2 = m_2^{‘}g,] где (m_2^{‘}) – масса груза, подвешенного справа, во втором случае.
С учетом этого: (M_1 = m_1gcdot{3d_1}) и (M_2 = m_2^{‘}gcdot{d_2}).
Приравняв (M_1) и (M_2), получаем, что: [m_1gcdot{3d_1} = m_2^{‘}gcdot{d_2}] [3m_1d_1 = m_2^{‘}d_2] Выразим массу второго груза (m_2^{‘}): [displaystyle{m_2^{‘} = frac{3m_1d_1}{d_2}}] Заметим, что (displaystyle{frac{m_1d_1}{d_2} = m_1}) (это следует из условия равновесия рычага для первого случая). [m_2^{‘} = 3m_1] То есть, чтобы рычаг после увеличения длины плеча (d_1) в 3 раза сохранил равновесие, масса второго груза должна так же увеличиться в 3 раза.
Тогда его масса должна измениться на: [Delta m = m_2^{‘} — m_2 = 3m_2 — m_2 = 2m_2] [Delta m = 2cdot{0,5text{ кг}} = 1text{ кг }]

Ответ: 1

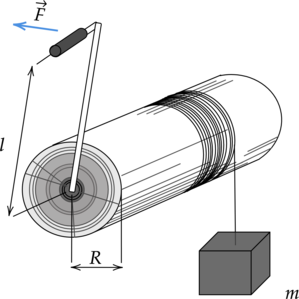
Какую силу (F) необходимо приложить, чтобы груз массой (m = 6) кг двигался вверх без ускорения, если радиус вала ворота (R = 24) см, а длина рукоятки (l = 0,36) м. Трением пренебречь. (Ответ дайте в Ньютонах.)

Т.к. груз движется без ускорения, то равнодействующая всех сил, действующих на груз, равна нулю. Поворот ворота обеспечивает подъем груза. В результате этого создается момент силы (F), длина плеча которой совпадает с длиной рукоятки (l), и он равен: [M_1 = Fl] Момент (M_1) уравновешивается моментом действующей на груз силы тяжести, длина плеча которой совпадает с радиусом вала ворота (R): [M_2 = mgcdot{R}] [Fl = mgcdot{R}] Отсюда выразим силу (F): [displaystyle{F = frac{mgcdot{R}}{l}}] [displaystyle{F = frac{6text{ кг}cdot{10text{ м/c}^2}cdot{0,24text{ м}}}{0,36text{ м}} = 40text{ Н }}]

Ответ: 40

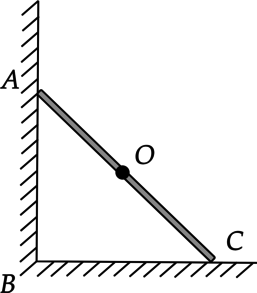
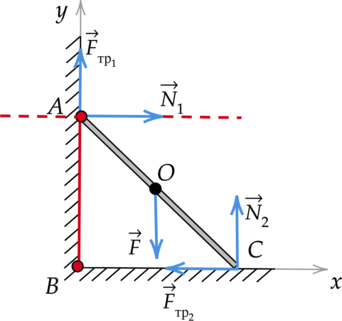
На однородный прут со стороны горизонтальной поверхности действует сила трения, равная 20 Н. Найдите момент силы реакции опоры, действующей на него со стороны вертикальной поверности, относительно оси, проходящей через точку (B) перпендикулярно плоскости рисунка, если (BC = 16) см, а (AC = 65) см. (Ответ дайте в Н(cdot)м и округлите до целого числа.)

Момент действующей на вертикальную стенку силы реакции опоры относительно оси, перпендикулярной плоскости рисунка и проходящей через точку (B), равен: [M = N_1l,] где (l) — плечо силы. Мысленно продолжим линию действия силы реакции опоры (N_1) и перпендикуляром соединим ее с прямой, проходящей через точку (B). Получаем, что плечом силы (N_2) является отрезок (AB), равный: [displaystyle{AB = sqrt{AC^2 — BC^2}}] [AB = sqrt{0,65text{ м}^2 — 0,16text{ м}^2} = 0,63text{ м }] Чтобы найти неизвестную величину (N_1), укажем все силы, действующие на прут, и запишем второй закон Ньютона с учетом того, что тело находится в равновесии: [vec{F}_{text{тр}1} + vec{N}_1 + vec{F} + vec{N}_2 + vec{F}_{text{тр}2} = 0] Введем оси (OX) и (OY), спроецируем на них все силы. [OX: N_1 — F_{text{тр}2} = 0] [OY: F_{text{тр}1} + N_2 — F = 0] Выразим силу реакции опоры (N_1), действующую на горизонтальную стенку: [N_1 = F_{text{тр}2}] [N_1 = 20text{ H}] Подставим найденные значения в начальную формулу: [M = 20{text{ Н}cdot{0,63}text{ м}} = 12,6text{ Н}cdot{text{м}}approx{13}text{ Н}cdot{text{м }}]

Ответ: 13

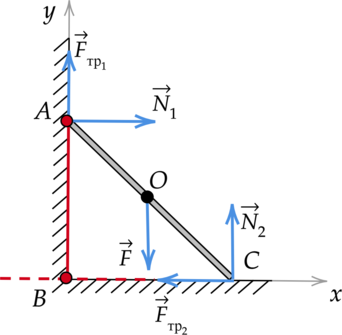
На однородный прут со стороны вертикальной поверхности действует сила реакции опоры, равная 125 Н. Найдите момент силы трения, действующей на него со стороны горизонтальной поверности, относительно оси, проходящей через точку (A) перпендикулярно плоскости рисунка, если (BC = 39) см, а (AC = 89) см. (Ответ дайте в кН(cdot)м.)

Момент действующей на прут со стороны горизонтальной стенки силы трения относительно оси, перпендикулярной плоскости рисунка и проходящей через точку (A), равен: [M = F_{text{тр}2}l,] где (l) — плечо силы. Мысленно продолжим линию действия силы реакции опоры (F_{text{тр}2}) и перпендикуляром соединим ее с прямой, проходящей через точку (A). Получаем, что плечом силы (F_{text{тр}2}) является отрезок (AB), равный: [displaystyle{AB = sqrt{AC^2 — BC^2}}] [AB = sqrt{0,89text{ м}^2 — 0,39text{ м}^2} = 0,8text{ м}] Чтобы найти неизвестную величину (F_{text{тр}2}), укажем все силы, действующие на прут, и запишем второй закон Ньютона с учетом того, что тело находится в равновесии: [vec{F}_{text{тр}1} + vec{N}_1 + vec{F} + vec{N}_2 + vec{F}_{text{тр}2} = 0] Введем оси (OX) и (OY), спроецируем на них все силы. [OX: N_1 — F_{text{тр}2} = 0] [OY: F_{text{тр}1} + N_2 — F = 0] Выразим силу трения (F_{text{тр}2}), действующую на горизонтальную стенку: [F_{text{тр}2} = N] [F_{text{тр}2} = 125text{ H }] Подставим найденные значения в начальную формулу: [M = 125{text{ Н}cdot{0,8}text{ м}} = 100text{ Н}cdot{text{м}} = 0,1text{ кН}cdot{text{м }}]

Ответ: 0,1

Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

“Демоверсия 2018”

Из правила моментов: [m1gl_1=m_2gl_2 Rightarrow l_2=m_1dfrac{l_1}{l_2}=0,2text{ кг}cdot 1,5=0,3text{ кг}] где (m_1) и (m_2) – массы грузов, (l_1) и (l_2) – расстояния от точки крепления грузов до точки подвеса.

Ответ: 0,3

Человек несёт груз на лёгкой палке (см. рисунок). Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA. Ответ дайте в см.

“Демоверсия 2020”

Из правила моментов: [F_1 cdot OA=F_2 cdot OB Rightarrow OA= dfrac{F_2cdot OB}{F_1}=dfrac{30text{ Н}cdot 80text{ см}}{80text{ Н}}=30text{ см}] Где (F_1) и (F_2) – силы, приложенные к концам ОА и ОВ соответственно.

Ответ: 30

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Статика твёрдого тела.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: момент силы, условия равновесия твёрдого тела.

Статика изучает равновесие тел под действием приложенных к ним сил. Равновесие — это состояние тела, при котором каждая его точка остаётся всё время неподвижной в некоторой инерциальной системе отсчёта.

Условием равновесия материальной точки является равенство нулю равнодействующей (т. е. векторной суммы) всех сил, приложенных к точке. В этом случае наша точка будет двигаться равномерно и прямолинейно в произвольной инерциальной системе отсчёта. Значит, система отсчёта, связанная с точкой, также будет инерциальной, и в ней точка будет покоиться.

В случае твёрдого тела ситуация сложнее. Прежде всего, важно учитывать точку приложения каждой силы.

-Сила тяжести приложена в центре тяжести тела. Для тела простой формы центр тяжести совпадает с центром симметрии.

-Силы упругости и трения приложены в точке или в плоскости контакта тела с соприкасающимся телом.

Прямая линия, проходящая через точку приложения вдоль вектора силы, называется линией действия силы. Оказывается, точку приложения силы можно переносить вдоль линии её действия — от этого механическое состояние тела не изменится (в частности, равновесие не нарушится).

Для равновесия твёрдого тела недостаточно потребовать равенства нулю векторной суммы всех приложенных к телу сил.

В качестве примера рассмотрим пару сил — так называются две равные по модулю противоположно направленные силы, линии действия которых не совпадают. Пусть пара сил $vec{F_{1}}$ и $vec{F_{2}}$ приложена к твёрдому стержню (рис. 1).

Рис. 1. Пара сил

Векторная сумма этих сил равна нулю. Но стержень покоиться не будет: он начнёт вращаться. В данном случае не выполнено второе условие равновесия твёрдого тела. Чтобы его сформулировать, нужно ввести понятие момента силы.

Как должна быть направлена линия действия силы, чтобы тело стало вращаться вокруг неподвижной оси? Для начала заметим следующее.

— Если линия действия силы параллельна данной оси, то вращения не будет.
— Если линия действия силы пересекает данную ось, то вращения не будет.

В каждом из этих случаев действие силы вызывает лишь деформацию твёрдого тела.

Чтобы началось вращение, линия действия силы и ось вращения должны быть скрещивающимися прямыми.

Без ограничения общности можно считать эти прямые перпендикулярными друг другу. Мы всегда можем этого добиться, разложив силу на две составляющие — параллельную и перпендикулярную оси вращения — и отбросив параллельную составляющую как не вызывающую вращения. Поэтому везде далее мы считаем, что все силы, действующие на тело, перпендикулярны оси вращения.

Момент силы.

Плечо силы — это расстояние от оси вращения до линия действия силы (т. е. длина общего перпендикуляра к двум этим прямым).

В качестве примера на рис. 2 изображён диск, к которому приложена сила vec{F} . Ось вращения перпендикулярна плоскости чертежа и проходит через точку . Плечом силы является величина l=OH , где — основание перпендикуляра, опущенного из точки на линию действия
силы.

Рис. 2. Плечо силы

Момент силы относительно оси вращения — это произведение силы на плечо:

M=Fl .

Чтобы учесть также направление вращения, вызываемого действием силы, моменту силы приписывают знак. Именно, момент силы считается положительным, если сила стремится поворачивать тело против часовой стрелки, и отрицательным, если по часовой стрелке.

Условия равновесия.

Если тело имеет неподвижную ось вращения и если алгебраическая сумма моментов всех сил относительно этой оси обращается в нуль, то тело будет находиться в равновесии. Это так называемое правило моментов . Оказывается, что в этом случае обращается в нуль алгебраическая сумма моментов всех сил относительно любой другой оси, параллельной оси вращения.

В общем случае, когда твёрдое тело может совершать как поступательное, так и вращательное движение, мы имеем два условия равновесия.

1. Равна нулю векторная сумма всех сил, приложенных к телу.
2. Равна нулю алгебраическая сумма моментов всех сил, приложенных к телу, относительно данной оси вращения или любой другой оси, параллельной данной.

Так, в примере на рис. 1 алгебраическая сумма моментов пары сил не обращается нуль (оба момента положительны). Поэтому стержень не находится в равновесии.

При решении задач удобно использовать сформулированные выше условия равновесия в следующем виде.

1′. Силы уравновешены вдоль любой оси.
2′. Суммарный момент сил, вращающих тело в одну сторону, равен суммарному моменту сил, вращающих тело в другую сторону.

Сейчас мы разберём одну достаточно содержательную задачу по статике и посмотрим, как работают наши условия равновесия.

Задача. Однородная лестница опирается на гладкую вертикальную стену, образуя с ней угол alpha . При каком максимальном значении alpha лестница будет покоиться? Коэффициент трения между лестницей и полом равен .

Решение. Пусть лестница опирается о пол и стену в точках и соответственно (рис. 3). Расставим силы, действующие на лестницу.

Рис. 3. К задаче

Поскольку лестница однородная, сила тяжести mvec{g} приложена в середине лестницы. Сила упругости пола $vec{N_{1}}$ и сила трения vec{f} приложены в точке . На рис. 3 точка приложения этих сил немного смещена от точки внутрь лестницы; тем самым мы однозначно указываем, что силы приложены именно к лестнице (а не к полу).

Точно так же сила упругости стены $vec{N_{2}}$ приложена в точке . Поскольку стена гладкая, сила трения между стеной и лестницей отсутствует.
Воспользуемся условием 1′. Вдоль горизонтальной оси силы уравновешены:

$f=N_{2}$ . (1)

Вдоль вертикальной оси силы также уравновешены:

$mg=N_{1}$ . (2)

Теперь переходим к правилу моментов — условию 2′. Какую ось вращения выбрать? Удобнее всего взять ось, проходящую через точку (перпендикулярно плоскости рисунка). В таком случае моменты сразу двух сил vec{f} и $vec{N_{1}}$ обратятся в нуль — ведь плечи этих сил относительно точки равны нулю (поскольку линии действия сил проходят через эту точку). Ненулевые моменты относительно точки имеют силы mvec{g} и $vec{N_{2}}$ , которые стремятся вращать лестницу в разные стороны; стало быть, моменты данных сил должны быть равны друг другу.

Плечо силы $vec{N_{2}}$ — это длина перпендикуляра , опущенного из точки на линию действия силы $vec{N_{2}}$ . Плечо силы mvec{g} — это длина перпендикуляра , опущенного из точки на линию действия силы mvec{g} . Согласно правилу моментов имеем:

$N_{2}cdot AC=mgcdot AD.$

Пусть длина лестницы равна . Тогда . Подставляем эти соотношения в равенство моментов:

$N_{2}cdot 2l cosalpha=mgcdot l sinalpha,$

откуда

$2N_{2}=mg tgalpha,$ (3)

С учётом равенства (1) имеем вместо (3):

(4)

Вспомним теперь, что в условии спрашивается максимальное значение alpha . При максимальном угле alpha лестница пока ещё стоит, но уже находится на грани проскальзывания. Это означает, что сила трения достигла своего максимального значения, равного силе трения скольжения:

$f=mu N_{1}$ .

Теперь из (4) получаем:

$2mu N_{1}=mg tgalpha$ ,

а с учётом равенства (2):

Отсюда получаем искомую максимальную величину alpha :

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Статика твёрдого тела.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Данная тема посвящена решению задач
на тему «Момент силы. Условия равновесия твердого тела».

Задача 1. Однородный сплошной кубик установлен так, что
одним своим ребром он опирается на вертикальную стену, а другим ребром
— на горизонтальный пол. Кубик находится в равновесии. На рисунке
показаны силы, которые действуют на кубик. Относительно каких точек,
обозначенных на рисунке, момент силы трения кубика о пол равен нулю?

РЕШЕНИЕ

Момент силы относительно некоторой точки определяется,
как произведение модуля этой силы на ее плечо.

Плечо — это длина перпендикуляра, опущенного
из рассматриваемой точки, на линию действия силы.

Модуль силы трения отличен
от нуля. Поэтому момент этой силы равен нулю только относительно таких
точек, относительно которых ее плечо равно нулю. То есть нас интересуют
только точки, лежащие на линии действия силы. А таких точек две — это точки
В и С.

ОТВЕТ: относительно точек В и С.

Задача 2. На поверхности земли находится две опоры на
расстоянии 5 м друг от друга. На эти опоры кладут горизонтальную балку массой
150 кг и длиной 8 м так, что 3 м балки выступают за правую опору. Определите
силу давления балки на эту опору.

Задача 3. Определите все силы, действующие на лестницу,
прислоненную к вертикальной стене. Масса лестницы m, а ее
центр тяжести располагается ровно посередине. При какой величине угла лестница
начнет скользить, если коэффициенты трения о пол и о стену одинаковы и равны μ?

«Ничто не мешает
человеку завтра

стать умнее, чем он
был вчера»

П.Л. Капица

Источник

Как известно, вся классическая механика делится на кинематику, динамику и статику. Про кинематику и динамику мы уже писали, а сегодня расскажем про статику и займемся решением задач.

Не забывайте подписаться на наш телеграм-канал и получать полезную рассылку каждый день.

Задачи на статику и равновесие тел

Мы не будем решать страшные задачи по теормеху, сопротивлению материалов или предмету ~~Тут Моя Могила~~ Теория Машин и Механизмов (ТММ). Разберем несколько примеров, связанных с равновесием и простейшими механизмами.

Именно на базе статики строится знаменитый сопромат, столь нелюбимый технарями.

Задача №1. Момент силы

Условие

На рычаг в состоянии равновесия действуют две силы. Момент первой равен 20 Н*м. Модуль второй силы равен 5 Н. Найдите плечо второй силы.

Решение

Запишем условие равновесия рычага:

Отсюда:

Ответ: 4м.

Задача №2. Статика

Условие

На концах рычага действуют силы с модулями 20 и 120 Н соответственно. Рычаг находится в равновесии. Найдите длину рычага, если расстояние от точки опоры до большей силы равно 2 см.

Решение

Запишем равенство моментов:

Ответ: 14 см.

В этой задаче мы не переводили размерности в систему СИ.

Задача №3. Расчет силы

Условие

Рабочий на стройке поднимает плиту с помощью рычага. Большее плечо равно 2,4м, меньшее — 0,8м. Какую силу прикладывает рабочий к большему плечу рычага, если масса плиты равна 120 кг?

Решение

Обозначим большее плечо через d1. К нему рабочий прикладывает искомую силу F1. Вторая сила, приложенная к меньшему плечу, равна весу плиты.

Ответ: 400 Н.

Задача№4. Подвижный блок

Условие

Какую силу нужно приложить, чтобы поднять груз весом 1000 Н с помощью подвижного блока? Какую работу совершит эта сила при подъеме груза на 1 метр?

Подвижный блок позволяет выиграть в усилии в два раза.

Решение

Найдем силу и работу:

Ответ: 500 Н, 1000 Дж.

Задача №5. Нахождение плеча рычага

Условие

На плечи рычага действуют силы 300 Н и 20 Н. Меньшее плечо равно 5см. Найдите большее плечо рычага.

Решение

Условие равновесия рычага можно записать так:

Ответ: 75 см.

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Вопросы и ответы по статике

Вопрос 1. Что нужно, чтобы тело находилось в равновесии, каково условие равновесия тел?

Ответ. Из законов Ньютона известно, что тело движется равномерно или покоится, если равнодействующая всех сил, приложенных к нему, равна нулю. Это и есть условие равновесия.

Это условие справедливо только для тела, которое может двигаться поступательно, но не может вращаться вокруг некоторой оси.

Вопрос 2. Каково условие равновесия для вращающихся тел?

Ответ. Если тело имеет неподвижную ось вращения, то оно находится в равновесии, если алгебраическая сумма моментов всех сил, приложенных к телу относительно этой оси, равна нулю.

Вопрос 3. Что такое момент силы?

Ответ. Момент силы — скалярная физическая величина, равная произведению модуля силы F на плечо силы d.

Вопрос 4. Что такое плечо силы?

Ответ. Плечо силы — это длина перпендикуляра, проведенного от оси вращения к линии действия силы.

Вопрос 5. Материальные тела в статике считаются упругими, или абсолютно твердыми?

Ответ. Абсолютно твердыми. Деформации и изменение размеров тела под действием сил не принимаются во внимание при решении задач, если иное не оговорено в условии.

Вопрос 6. Что такое рычаг в механике?

Ответ. Рычаг — простейший механизм. Рычагом может быть любое тело, которое может вращаться вокруг неподвижной опоры или подвеса. Используется для создания большего усилия на меньшем плече за счет меньшего усилия на длинном плече.

Статика: определение

Статика — раздел теоретической механики, изучающий основы равновесия тел.

Нужна помощь в решении более сложных заданий? Не знаете, как решать задачи по теоретической механике? Обращайтесь в профессиональный студенческий сервис.

Источник

Легче всего решать задачу, если все приложенные к телу силы параллельны – тогда можно получить ответ, используя лишь правило моментов. Если же силы непараллельные, то иногда для получения ответа требуется дополнительно применять второй закон Ньютона.

Параллельные силы

Алгоритм решения задач на правило моментов (параллельные силы)

Выполнить чертеж. Указать на нем все силы с точкой их приложения и направлением действия. В этом вам поможет таблица.

Сила	Точка приложения	Направление
Сила тяжести, действующая на груз	Центр груза	Вертикально вниз
Сила тяжести, действующая на однородный стержень	Центр тяжести	Вертикально вниз
Сила тяжести, действующая на неоднородный стержень	Центр масс, положение которого указывают в условии задачи	Вертикально вниз
Вес	Точка опоры или подвеса	Вес тела направлен противоположно вектору силы нормальной реакции опоры или вектору силы натяжения подвеса
Сила реакции опоры	Точка соприкосновения стержня и опоры	Перпендикулярно вверх
Сила натяжения нити	Точка соединения с подвесом	Вдоль оси подвеса

Выбрать положение оси вращения. Обычно ось выбирают в месте, где находится неизвестная сила или сила, искать которую не нужно.
Указать значение плеч. Если в задаче нужно указать некоторое расстояние (к примеру, от центра стержня или от места приложения некоторой силы), то это расстояние следует обозначать за x. Размер плеч сил нужно определять с учетом размеров стержня и расстояния x.
Записать правило моментов и решить задачу.

Типовы задачи на правило моментов при параллельных силах

Прямая неоднородная балка длиной l и массой m подвешена за концы на вертикально натянутых тросах. Балка занимает горизонтальное положение. Найдите силу натяжения первого троса T₂, если центр тяжести балки находится на расстоянии a от левого конца балки.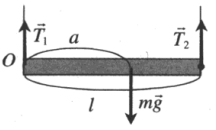

Для решения задачи в качестве положения оси вращения удобно выбрать точку приложения силы натяжения первого троса (потому что ее искать не нужно). Тогда плечом силы тяжести будет расстояние a, а плечом силы натяжения второго троса — l. Поэтому правило моментов можно записать так:

T₂l = mga

T₂ = mga/l

Рельс длиной l и массой m поднимают равномерно в горизонтальном положении на двух вертикальных тросах, первый из которых укреплен на конце рельса, а второй — на расстоянии x от другого конца. Определите натяжение второго троса.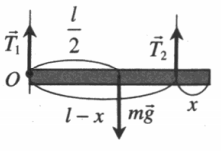

В этой задаче положение оси вращения также удобно выбрать в точке О, соответствующей точке приложения силы натяжения нити первого троса (так как ее искать не нужно). Тогда плечом силы натяжения второго троса будет служить разность длины рельса и расстояния x, а плечом силы тяжести — половина длины рельса. Поэтому правило моментов примет вид:

mgl/2 = T₂(l – x)

T2 = mgl2(l−x)

Пример №1. К левому концу невесомого стержня прикреплен груз массой 3 кг (см. рисунок). Стержень расположили на опоре, отстоящей от груза на 0,2 длины. Груз какой массы надо подвесить к правому концу, чтобы стержень находился в равновесии?

Условие равновесие будет выполняться, если произведение силы тяжести первого груза на ее плечо будет равно произведению силы тяжести второго груза на ее плечо:

F_тяж1d₁= F_тяж2d₂

Согласно рисунку, второй груз будет подвешен на расстоянии 0,8 от опоры. Следовательно:

Fтяж2=Fтяж2d1d2=m1gd1d2

m2g=m1gd1d2

m2=m1d1d2=3·0,20,8=0,75 (кг)

Непараллельные силы

Алгоритм решения задач на правило моментов (непараллельные силы)

Выполнить чертеж и указать все силы. Правильно определить точку приложения и направление сил поможет таблица:

Сила	Точка приложения	Направление
Сила реакции опоры	Точка соприкосновения с опорой	Перпендикулярно плоскости опоры
Сила трения покоя	Точка соприкосновения с опорой	В сторону возможного движения
Сила тяжести	Центр масс (у однородных тел центр масс совпадает с центром тела)	Вертикально вниз
Архимедова сила	Центр масс погруженной части тела	Вертикально вверх

Определить плечи сил как кратчайшее расстояние между осью вращения и направлением действия силы.
Записать правило моментов и решить задачу.

Внимание! Иногда для решения задачи может потребоваться использование второго закона Ньютона в проекциях на оси Ox и Oy.

Типовы задачи на правило моментов при непараллельных силах

Рабочий удерживает за один конец доску массой m так, что она образует угол α с горизонтом, опираясь о землю другим концом. С какой силой рабочий удерживает доску, если эта сила перпендикулярна доске?	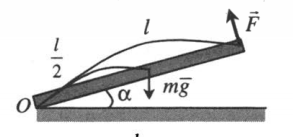За точку равновесия примем точку касания доски с землей. Плечо силы тяжести будет равно нижнему катету треугольника, образованного при опускании перпендикуляра к земле из точки приложения этой силы: d₁ = l cosα/2 Плечо силы, с которой рабочий поднимает доску, равно длине доски: d₂ = l Отсюда: mglcosα2=Fl F=2lmglcosα=2mgcosα
В гладкий высокий цилиндрический стакан с внутренним радиусом R помещают карандаш длиной l и массой m. С какой силой действует на стакан верхний конец карандаша?	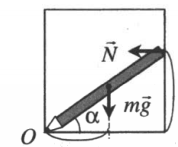За точку равновесия примем нижнюю точку карандаша. Сила давления верхнего конца карандаша на стакан по модулю будет равна силе нормальной реакции опоры в этой точке. Поэтому плечо ее силы будет равно произведению длины карандаша на синус угла между ним и дном стакана: d₁ = l sinα Минимальным расстоянием между линией действия силы тяжести и точкой равновесия будет половина произведения длины карандаша на косинус угла между ним и дном стакана: d₂ = l сosα/2 Отсюда: Nl sinα = mgl сosα/2 N=mglcosα2lsinα Плечо силы тяжести также равно радиусу стакана, а плечо силы реакции опоры можно найти из теоремы Пифагора. Отсюда: N=mgR√l2−4R2
Колесо радиусом R и массой m стоит перед ступенькой высотой h. Какую наименьшую горизонтальную силу надо приложить, чтобы оно могло подняться на ступеньку? Сила трения равна нулю.	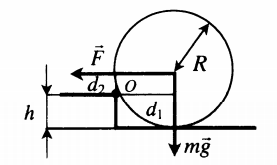За точку равновесия примем точку касания колеса со ступенькой. Плечо силы тяжести является катетом треугольника, образованного с радиусом колеса и плечом прикладываемой силы. Плечо этой силы равно разности радиуса и высоты ступеньки. d1=√R2−d22 d2 = R – h Отсюда: mg√R2−d22=F(R−h) F=mg√R2−d22R−h=mg√h(2R−h)R−h
Лестница массой m приставлена к гладкой вертикальной стене пол углом α. Найдите силу давления лестницы на стену. Центр тяжести лестницы находится в ее середине.	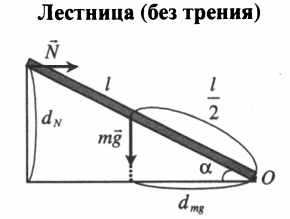Плечо силы тяжести равно половине произведения длины лестницы на косинус угла α. Плечо силы реакции опоры равно произведению этой длины на синус α. Поэтому правило моментов записывается так: Nlsinα=mglcosα2 Отсюда: N=mglcosα2lsinα=mg2tanα
Лестница длиной l приставлена к идеально гладкой стене под углом α к горизонту. Коэффициент трения между лестницей и полом μ. На какое расстояние x вдоль лестницы может поднять человек, прежде чем лестница начнет скользить? Массой лестницы пренебречь.	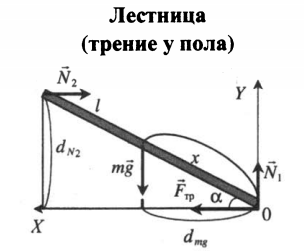Правило моментов: mgxcosα=N2lsinα Второй закон Ньютона в проекциях на оси Ox и Oy соответственно: F_тр – N₂ = 0 N₁ – mg = 0 Сила трения: F_тр = μmg = N₂ Следовательно: mgxcosα=μmglsinα x=μmglsinαmgxcosα=μltanα
Однородная лестница приставлена к стене. При каком наименьшем угле α между лестницей и горизонтальным полом лестница сохранит равновесие, если коэффициент трения между лестницей и полом μ₁, а между лестницей и стеной — μ₂?	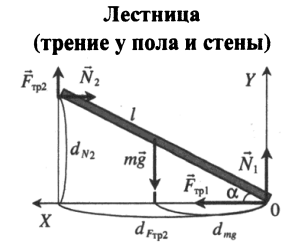Правило моментов: mgl2cosα=Fтр2lcosα+N2lsinα Второй закон Ньютона в проекциях на ось Ox: F_тр1 – N₂ = 0 μ₁N₁ – N₂ = 0 На ось Oy: F_тр2+ N₁ – mg = 0 μ2N2 +N2μ1 = mg N2(μ2+1μ1)=mg N2=mgμ2+1μ1=mgμ1μ1μ2+1 Fтр2=mg−N1=mg−N2μ1=mg−mgμ1μ2+1=mg(1−1μ1μ2+1) mgl2cosα=mg(1−1μ1μ2+1)lcosα+mgμ1μ1μ2+1lcosα Преобразуем выражение и получим: tanα=1−μ1μ21μ1
Какую минимальную горизонтальную силу нужно приложить к верхнему ребру куба массой m, находящегося на горизонтальной плоскости, чтобы перекинуть его через нижнее ребро?	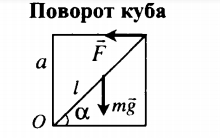Правило моментов примет вид: mgl2cosα=Flsinα У куба угол α равен 45 градусам, а синус и косинус этого угла равны. Длины диагонали взаимоуничтожаются. Остается: F=mg2

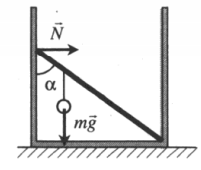
Пример №2. Невесомый стержень длиной 1 м, находящийся в ящике с гладким дном и стенками, составляет угол α = 45^о с вертикалью (см. рисунок). К стержню на расстоянии 25 см от его левого конца подвешен на нити шар массой 2 кг. Каков модуль силы N, действующий на стержень со стороны левой стенки ящика?

25 см = 0,25 м

Пусть точкой равновесия будет точка касания нижнего конца стержня с дном ящика. Тогда плечом силы тяжести будет:

d₁ = (l – 0,25)sinα

Плечом силы реакции опоры будет:

d₂ = l cosα

Запишем правило моментов:

mg(l−0,25)sinα=Nlcosα

Отсюда:

N=mg(l−0,25)sinαlcosα

Так как косинус и синус угла 45^о равны, получим:

N=mg(l−0,25)l=2·10(1−0,25)1=15 (Н)

Задание EF17982

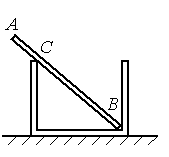
Однородный стержень АВ массой 100 г покоится, упираясь в стык дна и стенки банки концом В и опираясь на край банки в точке С (см. рисунок). Модуль силы, с которой стержень давит на стенку сосуда в точке С, равен 0,5 Н. Чему равен модуль горизонтальной составляющей силы, с которой стержень давит на сосуд в точке В, если модуль вертикальной составляющей этой силы равен 0,6 Н? Трением пренебречь.

Ответ:

а) 0,3 Н

б) 0,25 Н

в) 0,6 Н

г) 0,13 Н

Алгоритм решения

Записать исходные данные и перевести единицы измерения величин в СИ.
Выполнить чертеж. Выбрать ось вращения. Указать силы и их плечи.
Использовать второй и третий законы Ньютона, чтобы выполнить общее решение.
Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

Масса стержня: m = 100 г.
Модуль силы, с которой стержень давит на стенку сосуда в точке С: F_C = 0,5 Н.
Модуль вертикальной составляющей силы, с которой стержень давит на сосуду в точке В: F_By = 0,6 Н.

Переведем единицы измерения в СИ:

100 г = 0,1 кг

Выполним чертеж:

Поскольку стержень покоится, согласно второму закону Ньютона, равнодействующая всех сил, действующих на него, должна быть равна нулю. На стержень действует три силы:

сила тяжести (mg);
сила реакции опоры в точке С (F_C);
сила реакции опоры в точке В (F_В).

Поэтому:

m→g+→FC+→FB=0

Запишем проекции на оси Ox и Oy соответственно:

FCx=FBx

FCy+FBy=mg

Модуль горизонтальной составляющей силы в точке В можно выразить через теорему Пифагора:

FCx=√F2C−F2Cy

Но вертикальная составляющая силы в точке C равна разности силы тяжести и горизонтальной составляющей силы в точке В:

FCy=mg−FBy

Отсюда:

FBx=FCx=√F2C−F2Cy=√F2C−(mg−FBy)2

Подставим известные данные и вычислим:

FBx=√0,52−(0,1·10−0,6)2=√0,25−0,16=0,3 (Н)

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

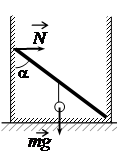
Задание EF18697

Невесомый стержень, находящийся в ящике с гладкими дном и стенками, составляет угол 45° с вертикалью (см. рисунок). К середине стержня подвешен на нити шарик массой 1 кг. Каков модуль силы упругости N, действующей на стержень со стороны левой стенки ящика?

Алгоритм решения

1.Записать исходные данные.

2.Записать правило моментов.

3.Выполнить решение в общем виде.

4.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Угол между стержнем и стенкой ящика: α = 45^o.

• Масса шарика: m = 1 кг.

Чтобы записать правило моментов, нужно определить плечи силы тяжести и силы упругости. В качестве точки равновесия выберем точку опоры нижнего конца стержня. Тогда плечо силы тяжести будет равно произведению половины длины стержня на косинус угла между дном ящика и стержнем. Он тоже будет равен 45 градусам, так как он равен разности 180 градусов и угла α = 45^o. Отсюда:

dmg=l2cosα

Плечо силы упругости будет равно расстоянию от дна ящика до верхней точки стержня. Оно определяется как произведение длины стержня на синус угла α:

dN=lsinα

Запишем правило моментов:

mgl2cosα=Nlsinα

Отсюда:

N=mgl2lsinαcosα

Длина стержня в числителе и знаменателе сократится, косинус и синус угла тоже, так как при 45 градусах они одинаковые. Следовательно:

N=mg2=1·102=5 (Н)

Ответ: 5

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 7.2k

Источник

Задачи на простые механизмы с решениями

Название величины

Обозначение

Единица измерения

Формула

Сила

F

Н

F1l1 = F2l2

Плечо силы

l

м

Момент силы

M

Нм

M = Fl

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Краткая теория для решения задачи на простые механизмы.

Статика твёрдого тела.

Момент силы.

Условия равновесия.

Задачи на статику и равновесие тел

Задача №1. Момент силы

Задача №2. Статика

Задача №3. Расчет силы

Задача№4. Подвижный блок

Задача №5. Нахождение плеча рычага

Вопросы и ответы по статике

Статика: определение

Параллельные силы

Типовы задачи на правило моментов при параллельных силах

Непараллельные силы

Типовы задачи на правило моментов при непараллельных силах

Новое и интересное на сайте:

F₁l₁ = F₂l₂