Егэ физика механика презентация - Помощь в подготовке к экзаменам и поступлению

Скачать материал

Сейчас обучается 34 человека из 20 регионов

Сейчас обучается 63 человека из 37 регионов

Сейчас обучается 46 человек из 28 регионов

Описание презентации по отдельным слайдам:

1 слайд

Подготовка к ЕГЭ. Решение типовых задач разного уровня.
Подготовила: Бочкова Любовь Ивановна, учитель физики
3 слайд

2. Зависимость от времени координат четырёх тел, движущихся по оси ОХ, представлены в таблице Покоилось тело : 1) 1; 2) 2; 3) 3; 4) 4.
4 слайд

3. Зависимость от времени координат четырёх тел, движущихся по оси ОХ, представлены в таблице В отрицательном направлении оси ОХ двигалось тело: 1)1; 2) 2; 3) 3; 4) 4.
5 слайд

На рисунке изображён график скорости переменного движения. Модуль ускорения максимален на промежутке времени
1)0-t1 2) t2-t3, 3) t3-t4, 4) t4-t5.
6 слайд

Используя график зависимости скорости тела от времени, определите скорость тела в начале 6-й секунды, считая, что характер движения не измениться.
2,5 м/с; 2) 3 м/с; 3) 3,5 м/с; 4) 4 м/с.
7 слайд

Маленький шарик падает вертикально вниз и ударяется о наклонную плоскость, затем отскакивает от неё в горизонтальном направлении. Импульс шарика перед ударом равен 4 кг м/с импульс шарика после удара 3 кг м/с. Модуль изменения импульса шарика равен: 1) 1 кг м/с; 2) 3,5 кг м/с; 3) 5 кг м/с; 7 кг м/с.
8 слайд

Маленький шарик падает вертикально вниз и ударяется о
наклонную плоскость, затем отскакивает от неё в
горизонтальном направлении. Импульс шарика перед ударом
равен 4 кг м/с импульс шарика после удара 3 кг м/с. Модуль
изменения импульса шарика равен:
1) 1 кг м/с; 2) 3,5 кг м/с; 3) 5 кг м/с; 7 кг м/с.

Дано Решение
v1=4 кг м/с Обозначим начальный импульс р1, конечный – р2.
v2=3 кг м/с Изменение импульса Δ p находится как разность между
Δ p-? конечным и начальным импульсами.
9 слайд

Две тележки массами 20 кг и 30 кг движутся навстречу друг другу, первая со скоростью 1 м/с, вторая – со скоростью 1, 5 м/с. Модуль импульса системы этих тел после абсолютно неупругого удара равен
0; 2) 25 кг м/с; 3) 62,5 кг м/с; 4) 65 кг м/с.
10 слайд

Две тележки массами 20 кг и 30 кг движутся навстречу друг другу, первая со скоростью 1 м/с, вторая – со скоростью 1, 5 м/с. Модуль импульса системы этих тел после абсолютно неупругого удара равен
0; 2) 25 кг м/с; 3) 62,5 кг м/с; 4) 65 кг м/с.

Дано Решение
m1=20 кг По закону сохранения импульса для замкнутых систем тел векторная
m2-30 кг сумма импульсов не изменяется, р10х+р20х=р1х+р2х
v1=1 м/с 20х1-30х1,5=-25 кг м/с
v2=1,5 м/с Ответ: 2.
p-?
11 слайд

На рисунке приведен график зависимости скорости велосипедиста от времени. Путь, пройденный велосипедистом за 20 с, равен
1) 125 м 2) 200 м, 3) 225 м, 4) 300 м
12 слайд

На рисунке приведен график зависимости скорости велосипедиста от времени. Путь, пройденный велосипедистом за 20 с, равен
1) 125 м 2) 200 м, 3) 225 м, 4) 300 м
Решение:
Путь, пройденный телом, численно равен площади фигуры, образующейся под графиком зависимости скорости от времени
S=1/2х(5х10)+10х20=225 м
Ответ: 3.
13 слайд

На рисунке представлены вектор скорости и вектор равнодействующих всех сил, действующих на тело. Какой из четырех векторов на рисунке указывает направление вектора ускорения этого тела в инерциальной системе отсчёта?
1 2) 2 3) 3 4) 4
14 слайд

На рисунке представлены вектор скорости и вектор равнодействующих всех сил, действующих на тело. Какой из четырех векторов на рисунке указывает направление вектора ускорения этого тела в инерциальной системе отсчёта?
1 2) 2 3) 3 4) 4
Решение
По второму закону Ньютона
F=ma. Следовательно сила
сонаправлена с ускорением.
Ответ:2.
15 слайд

На тележке , двигающейся с постоянным ускорением 0,5 м/с2, покоится брусок. Со стороны тележки на брусок действует сила трения 1,5 Н. Сила трения, действующая со стороны бруска на тележку равна
1) 0 Н 2) 0,5 Н 3), 1,5 Н 4) 3 Н.
16 слайд

Два тела движутся со скоростями 4 м/с и 3 м/с, по взаимно перпендикулярным траекториям. Модуль их скорости относительно друг друга равен
1) 1 м/с, 2) 5 м/с, 3) 7 м/с, 4) 25 м/с.
17 слайд

Два тела движутся со скоростями 4 м/с и 3 м/с, по взаимно перпендикулярным траекториям. Модуль их скорости относительно друг друга равен
1 м/с, 2) 5 м/с, 3) 7 м/с, 4) 25 м/с.

Дано Решение
V1=4 м/с
V2= 3 м/с
V12-?
18 слайд

Два тела движутся со скоростями 4 м/с и 3 м/с, по взаимно перпендикулярным траекториям. Модуль их скорости относительно друг друга равен
1 м/с, 2) 5 м/с, 3) 7 м/с, 4) 25 м/с.

Дано Решение
V1=4 м/с
V2= 3 м/с
V12-?

V12=5 м/с
Ответ: 5 м/с.
19 слайд

Тело движется по прямой. Под действием постоянной силы величиной 4 Н за 2 с импульс тела увеличился и стал равен 20 кг м/с. Первоначальный импульс тела равен
1) 4 кг м/с, 2) 8 кг м/с, 3) 12 кг м/с, 4) 28 кг м/с
20 слайд

Тело движется по прямой. Под действием постоянной силы величиной 4 Н за 2 с импульс тела увеличился и стал равен 20 кг м/с. Первоначальный импульс тела равен
4 кг м/с, 2) 8 кг м/с, 3) 12 кг м/с, 4) 28 кг м/с.
Дано Решение
F=4 Н по второму закону Ньютона
t=2c F=ma=m(v-v0)/t=(mv-mv0)/t=
p2=20 кг м/с = (p2-p1)/t, p1=p2-Ft, p1=20-4×2=
р1-? =12 кг м/с
Ответ: 3.
21 слайд

На рисунке схематически изображена лестница АС, прислоненная к стене. Каков модуль момента силы тяжести F, действующей на лестницу относительно точки С?
1) Fx OC, 2) FxOD, 3) FxAC, 4) FxDC
22 слайд

На рисунке схематически изображена лестница АС, прислоненная к стене. Каков модуль силы тяжести F, действующей на лестницу относительно точки С?
1) Fx OC, 2) FxOD, 3) FxAC, 4) FxDC
Решение
По определению, модуль момента силы относительно оси равен произведению модуля силы на плечо (длину перпендикуляра, соединяющего ось с линией действия силы). Как видно из рисунка в условии задачи, модуль момента силы равен M=FxDC.
Ответ:4.
23 слайд

Задача.
В широкую U-образную трубку с вертикальными прямыми коленами налиты керосин плотностью q1=0,8×103 кг/м3 и вода плотностью q2= 1х103 кг/м3. На рисунке b=10 см, H= 30 см. Расстояние h равно
1) 16 см, 2) 20 см, 3) 24 см, 4) 26 см
24 слайд

В широкую U-образную трубку с вертикальными прямыми коленами налиты керосин плотностью q1=0,8×103 кг/м3 и вода плотностью q2= 1х103 кг/м3. На рисунке b=10 см, H= 30 см. Расстояние h равно
1) 16 см, 2) 20 см, 3) 24 см, 4) 26 см.

Дано Решение
q1=0,8×103 кг/м3 Т.к. сосуды сообщающиеся, в обоих коленах
q2= 1х103 кг/м3 одинаковое давление жидкости .
b=0,10 м
H= 0,30 м
h -?
25 слайд

В широкую U-образную трубку с вертикальными прямыми коленами налиты керосин плотностью q1=0,8×103 кг/м3 и вода плотностью q2= 1х103 кг/м3. На рисунке b=10 см, H= 30 см. Расстояние h равно
1) 16 см, 2) 20 см, 3) 24 см, 4) 26 см.

Дано Решение
q1=0,8×103 кг/м3 Т.к. сосуды сообщающиеся, в обоих коленах
q2= 1х103 кг/м3 одинаковое давление жидкости . В левом колене налиты
b=0,10 м две жидкости, поэтому р1 = q1g(H-b)+ q2 gb.
H= 0,30 м
h -?
26 слайд

В широкую U-образную трубку с вертикальными прямыми коленами налиты керосин плотностью q1=0,8×103 кг/м3 и вода плотностью q2= 1х103 кг/м3. На рисунке b=10 см, H= 30 см. Расстояние h равно
1) 16 см, 2) 20 см, 3) 24 см, 4) 26 см.

Дано Решение
q1=0,8×103 кг/м3 Т.к. сосуды сообщающиеся, в обоих коленах
q2= 1х103 кг/м3 одинаковое давление жидкости . В левом колене налиты
b=0,10 м две жидкости, поэтому р1 = q1g(H-b)+ q2 gb.
H= 0,30 м В правом колене р2=q2 gh. р1 =р2,
h -? q1g(H-b)+ q2 gb= q2 gh, h=q1/ q2 (H-b)+ b
h=0,8(0,3-0,1)+0,1= 0,26=26 см.
Ответ: 4.
27 слайд

Математический маятник совершает малые колебания. В таблице представлены координаты маятника для различных промежутков времени. Длина нити маятника приблизительно равна
1) 30 см, 2) 45 см, 3) 50 см, 4) 65 см
28 слайд

Математический маятник совершает малые колебания. В таблице представлены координаты маятника для различных промежутков времени. Длина нити маятника приблизительно равна
1) 30 см, 2) 45 см, 3) 50 см, 4) 65 см
Дано Решение
π =3,14 Воспользуемся формулой периода T=2π .
g=9,8 м/с2 По определению периода Т=1,6 с.

L-? L= , L=0,65 м

Ответ: 4.
29 слайд

Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина при этом всё время остаётся растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия? Для каждой величины определите соответствующий характер изменения:
1) увеличивается, 2) уменьшается, 3) не изменяется.
30 слайд

Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина при этом всё время остаётся растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия? для каждой величины определите соответствующий характер изменения:
1) увеличивается, 2) уменьшается, 3) не изменяется.
31 слайд

Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина при этом всё время остаётся растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия? для каждой величины определите соответствующий характер изменения:
1) увеличивается, 2) уменьшается, 3) не изменяется.
32 слайд

Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина при этом всё время остаётся растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия? для каждой величины определите соответствующий характер изменения:
1) увеличивается, 2) уменьшается, 3) не изменяется.
33 слайд

Задача.

Груз массой 100 кг удерживается на месте с помощью рычага, приложив вертикальную силу 350 Н. Рычаг состоит из шарнира без трения и однородного массивного стержня длиной 5 м.
Расстояние от оси шарнира до точки подвеса груза равно 1 м.
Масса стержня равна
1) 25 кг, 2) 35 кг, 3) 20 кг, 4) 30 кг
34 слайд

Задача.
Груз массой 100 кг удерживается на месте с помощью рычага,
приложив вертикальную силу 350 Н. Рычаг состоит из шарнира
без трения и однородного массивного стержня длиной 5 м.
Расстояние от оси шарнира до точки подвеса груза равно 1 м.
Масса стержня равна
1) 25 кг, 2) 35 кг, 3) 20 кг, 4) 30 кг
Дано Решение

L=5 м FL-Mgb-mgL/2=0
F=350H m=2(FL-Mgb)/gL=2(F/g-Mb/L)=2(350/10-100х1/5)=30 кг
M=100 кг
G=9,8 Н/кг Ответ: 4.
b= 1 м
m-?
35 слайд

Задача.
Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60 градусов и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару со скоростью 300 м/с. Она пробивает его и вылетает горизонтально со скоростью 200 м/с, после чего шар продолжает движение в прежнем направлении.
На какой максимальный угол отклонится шар после попадания в него пули? Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити.
36 слайд

Задача.

Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60 градусов и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару со скоростью 300 м/с. Она пробивает его и вылетает горизонтально со скоростью 200 м/с, после чего шар продолжает движение в прежнем направлении.
На какой максимальный угол отклонится шар после попадания в него пули? Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити.
Дано Решение
M=1 кг Обозначим u- скорость шара до попадания пули и u1- после попадания пули.
m=0,01 кг
v=300 м/с 1. По закону сохранения импульса Mu-mv=Mu1-mv1, u1=u+m/M(v1-v).
V1=200 м/с.
L= 0,9 м
α=60
β-?
37 слайд

Задача.
Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60 градусов и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару со скоростью 300 м/с. Она пробивает его и вылетает горизонтально со скоростью 200 м/с, после чего шар продолжает движение в прежнем направлении.
На какой максимальный угол отклонится шар после попадания в него пули? Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити.
Дано Решение
M=1 кг Обозначим u- скорость шара до попадания пули и u1- после попадания пули.
m=0,01 кг
v=300 м/с 1. По закону сохранения импульса Mu-mv=Mu1-mv1, u1=u+m/M(v1-v).
V1=200 м/с 2. По закону сохранения механической энергии для шара Еп=Ек или Mgh=Mu2/2. g=9,8 м/с2, gh=u2/2, 2gh=u2..
L= 0,9 м
α=60,
β-?

.
38 слайд

Задача.
Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60 градусов и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару со скоростью 300 м/с. Она пробивает его и вылетает горизонтально со скоростью 200 м/с, после чего шар продолжает движение в прежнем направлении.
На какой максимальный угол отклонится шар после попадания в него пули? Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити.
Дано Решение
M=1 кг Обозначим u- скорость шара до попадания пули и u1- после попадания пули.
m=0,01 кг
v=300 м/с 1. По закону сохранения импульса Mu-mv=Mu1-mv1, u1=u+m/M(v1-v).
V1=200 м/с 2. По закону сохранения механической энергии для шара Еп.=Ек или Mgh=Mu2/2. g=9,8 м/с2, gh=u2/2, 2gh=u2.
L= 0,9 м h=L-Lcos60=L(1-cos60), 2gL(1-cos60)=u2.
α=60
β-?
39 слайд

Задача.
Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60 градусов и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару со скоростью 300 м/с. Она пробивает его и вылетает горизонтально со скоростью 200 м/с, после чего шар продолжает движение в прежнем направлении.
На какой максимальный угол отклонится шар после попадания в него пули? Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити.
Дано Решение
M=1 кг Обозначим u- скорость шара до попадания пули и u1- после попадания пули.
m=0,01 кг
v=300 м/с 1. По закону сохранения импульса Mu-mv=Mu1-mv1, u1=u+m/M(v1-v).
V1=200 м/с 2. По закону сохранения механической энергии для шара Еп.=Ек или Mgh=Mu2/2. g=9,8 м/с2, gh=u2/2, 2gh=u2. Определим неизвестную высоту.
L= 0,9 м h=L-Lcos60=L(1-cos60), 2gL(1-cos60)=u2.
α=60 После столкновения с пулей Mu12/2=Mgh1, u12 =2gh1,
β-? h1=L(1-cos β ) , u12 =2g L(1-cos β ) , cos β =1- u12 /2gL=

=1 – 1/2gL( +m/M(v1-v))2=7/9.

Ответ: arccos(7/9)
40 слайд

Задача.
Ареометр, погруженный в жидкость совершает вертикальные гармонические колебания с малой амплитудой. Найдите период этих колебаний. Масса ареометра равна 40 г, радиус его трубки 2 мм, плотность жидкости 0,8 г/см3. Сопротивлением жидкости пренебречь .
41 слайд

Задача.
Ареометр, погруженный в жидкость совершает вертикальные гармонические колебания с малой амплитудой. Найдите период этих колебаний. Масса ареометра равна 40 г, радиус его трубки 2 мм, плотность жидкости 0,8 г/см3. Сопротивлением жидкости пренебречь .

Дано Решение
m=0,04 кг Период гармонических колебаний равен T=2π (1)
r=0,002 м Возвращающая сила задаётся уравнением F=-kx.
q=800 кг/м3
g=9,8 м/с2
T-?
42 слайд

Задача.
Ареометр, погруженный в жидкость совершает вертикальные гармонические колебания с малой амплитудой. Найдите период этих колебаний. Масса ареометра равна 40 г, радиус его трубки 2 мм, плотность жидкости 0,8 г/см3. Сопротивлением жидкости пренебречь .

Дано Решение
m=0,04 кг Период гармонических колебаний равен T=2π (1)
r=0,002 м Возвращающая сила задаётся уравнением F=-kx.
q=800 кг/м3 Найдём эту силу.
g=9,8 м/с2 В данной задаче этой силой является
T-? выталкивающая сила F=qgV=qgSx.
43 слайд

Задача.
Ареометр, погруженный в жидкость совершает вертикальные гармонические колебания с малой амплитудой. Найдите период этих колебаний. Масса ареометра равна 40 г, радиус его трубки 2 мм, плотность жидкости 0,8 г/см3. Сопротивлением жидкости пренебречь .

Дано Решение
m=0,04 кг Период гармонических колебаний равен T=2π (1)
r=0,002 м Возвращающая сила задаётся уравнением F=-kx.
q=800 кг/м3 Найдём эту силу.
g=9,8 м/с2 В данной задаче этой силой является
T-? выталкивающая сила F=qgV=qgSx.
На ареометр, смещенный от положения равновесия на расстояние х, действует возвращающая сила F=-qgSx (2)
где – qgSкоэффициент возвращающей силы.
Из уравнения (1) и (2) получаем: T=2/r, =2/0,002
Ответ: 4 с.
44 слайд

Задача.

На гладкой горизонтальной плоскости находится длинная доска массой М = 2 кг. По доске скользит шайба массой m = 0,5 кг. Коэффициент трения между шайбой и доской μ = 0,2. В начальный момент времени скорость шайбы υ0 = 2 м/с, а доска покоится. Сколько времени потребуется для того, чтобы шайба перестала скользить по доске?
45 слайд

Задача.
На гладкой горизонтальной плоскости находится длинная доска массой М = 2 кг. По доске скользит шайба массой m = 0,5 кг. Коэффициент трения между шайбой и доской μ = 0,2. В начальный момент времени скорость шайбы υ0 = 2 м/с, а доска покоится. Сколько времени потребуется для того, чтобы шайба перестала скользить по доске?

Дано Решение.
М = 2 кг Используя закон сохранения импульса тел
m = 0,5 кг при взаимодействии, получим m υ0 = (M + m) υ,
μ = 0,2 где υ – скорость доски в момент остановки шайбы на доске
υ0 = 2 м/с υ = m υ0/(M + m).
t — ?
46 слайд

Задача.
На гладкой горизонтальной плоскости находится длинная доска массой М = 2 кг. По доске скользит шайба массой m = 0,5 кг. Коэффициент трения между шайбой и доской μ = 0,2. В начальный момент времени скорость шайбы υ0 = 2 м/с, а доска покоится. Сколько времени потребуется для того, чтобы шайба перестала скользить по доске?

Дано Решение.
М = 2 кг Используя закон сохранения импульса тел
m = 0,5 кг при взаимодействии, получим m υ0 = (M + m) υ,
μ = 0,2 где υ – скорость доски в момент остановки шайбы на доске
υ0 = 2 м/с υ = m υ0/(M + m). Эту скорость доска приобрела
t — ? за время движения шайбы по доске υ = at под действием
силы трения шайбы о доску.
47 слайд

Задача.
На гладкой горизонтальной плоскости находится длинная доска массой М = 2 кг. По доске скользит шайба массой m = 0,5 кг. Коэффициент трения между шайбой и доской μ = 0,2. В начальный момент времени скорость шайбы υ0 = 2 м/с, а доска покоится. Сколько времени потребуется для того, чтобы шайба перестала скользить по доске?

Дано Решение.
М = 2 кг Используя закон сохранения импульса тел
m = 0,5 кг при взаимодействии, получим m υ0 = (M + m) υ,
μ = 0,2 где υ – скорость доски в момент остановки шайбы на доске
υ0 = 2 м/с υ = m υ0/(M + m). Эту скорость доска приобрела
t — ? за время движения шайбы по доске υ = at под действием
силы трения шайбы о доску. Сила трения, действующая на
шайбу, равна по модулю силе трения, действующей на доску
F= μ mg, следовательно, a =F /M = μ mg/M.
t = υ/a = M m υ0 / (M + m) μ mg = 0, 8 с.
Ответ: 0,8 с.
48 слайд

С высоты Н над землёй из состояния покоя начинает свободно падать стальной шарик, который через время t=0,4 с сталкивается с плитой, наклоненной под углом 30 градусов к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h=1,4 м над землёй. Чему равна высота Н? Сделайте схематический рисунок, поясняющий решение.
Задача.
49 слайд

С высоты Н над землёй из состояния покоя начинает свободно падать стальной шарик, который через время t=0,4 с сталкивается с плитой, наклоненной под углом 30 градусов к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h=1,4 м над землёй. Чему равна высота Н? Сделайте схематический рисунок, поясняющий решение.

Дано Решение
t=0,4 с 1) перед столкновением с плитой скорость шарика v=gt
h=1,4 м
V0=0
α=300
H-?
50 слайд

С высоты Н над землёй из состояния покоя начинает свободно падать стальной шарик, который через время t=0,4 с сталкивается с плитой, наклоненной под углом 30 градусов к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h=1,4 м над землёй. Чему равна высота Н? Сделайте схематический рисунок, поясняющий решение.

Дано Решение
t=0,4 с 1) перед столкновением с плитой скорость шарика v=gt
h=1,4 м 2) после столкновения направление скорости с горизонтом
V0=0 составляет угол β=900-2α
α=300
H-?
51 слайд

С высоты Н над землёй из состояния покоя начинает свободно падать стальной шарик, который через время t=0,4 с сталкивается с плитой, наклоненной под углом 30 градусов к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h=1,4 м над землёй. Чему равна высота Н? Сделайте схематический рисунок, поясняющий решение.

Дано Решение
t=0,4 с 1) перед столкновением с плитой скорость шарика v=gt
h=1,4 м 2) после столкновения направление скорости с горизонтом
V0=0 составляет угол β=900-2α
α=300 3)Vx=V10cos β =gtcos β =gtsin2α
H-? V10 –скорость перед ударом
52 слайд

С высоты Н над землёй из состояния покоя начинает свободно падать стальной шарик, который через время t=0,4 с сталкивается с плитой, наклоненной под углом 30 градусов к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h=1,4 м над землёй. Чему равна высота Н? Сделайте схематический рисунок, поясняющий решение.

Дано Решение
t=0,4 с 1) перед столкновением с плитой скорость шарика v=gt
h=1,4 м 2) после столкновения направление скорости с горизонтом
V0=0 составляет угол β=900-2α
α=300
g=9,8 м/с2 3)Vx=V10cos β =gtcos β =gtsin2α
H-? V10 –скорость перед ударом
4) Применим закон сохранения
энергии: Е0=mgH, E1=mgh+mvx2/2

mgH=mgh+mvx2/2, H=h+vx2/2g=h+ (gt2sin22α)/2
H=1,4+10х0,42sin600/2=2,1 м
Ответ: 2,1 м
53 слайд

Задача.
Грузы массами М =1 кг и m связаны лёгкой нерастяжимой нитью, переброшенной через блок, по которому нить может
скользить без трения. Груз массой М находится на
шероховатой наклонной плоскости ( угол наклона плоскости
к горизонту 30 градусов, коэффициент трения 0,3. Чему
равно максимальное значение массы m, при которой система грузов ещё не выходит из первоначального состояния покоя?
54 слайд

Задача.
Грузы массами М =1 кг и m связаны лёгкой нерастяжимой
нитью, переброшенной через блок, по которому нить может
скользить без трения. Груз массой М находится на
шероховатой наклонной плоскости ( угол наклона плоскости
к горизонту 30 градусов, коэффициент трения 0,3). Чему
равно максимальное значение массы m, при которой система
грузов ещё не выходит из первоначального состояния покоя?
Дано Решение
М=1 кг Будем считать систему, связанную с наклонной плоскостью
α=30 0 инерциальной. Для первого тела по 2 закону Ньютона
μ=0,3 ОХ: T1-Fтр-Mgsinα=0
m max-? Оу: N-Mgcosα=0
55 слайд

Задача.
Грузы массами М =1 кг и m связаны лёгкой нерастяжимой
нитью, переброшенной через блок, по которому нить может
скользить без трения. Груз массой М находится на
шероховатой наклонной плоскости ( угол наклона плоскости
к горизонту 30 градусов, коэффициент трения 0,3). Чему
равно максимальное значение массы m, при которой система
грузов ещё не выходит из первоначального состояния покоя?
Дано Решение
М=1 кг Будем считать систему, связанную с наклонной плоскостью
α=30 0 инерциальной. Для первого тела по 2 закону Ньютона
μ=0,3 ОХ: T1-Fтр-Mgsinα=0
m max-? Оу: N-Mgcosα=0

Для второго тела 2 закон Ньютона:
Оу: mg-T2=0. Т1=Т2=Т. Fтр ≤μN.
56 слайд

Задача.
Грузы массами М =1 кг и m связаны лёгкой нерастяжимой
нитью, переброшенной через блок, по которому нить может
скользить без трения. Груз массой М находится на
шероховатой наклонной плоскости ( угол наклона плоскости
к горизонту 30 градусов, коэффициент трения 0,3). Чему
равно максимальное значение массы m, при которой система
грузов ещё не выходит из первоначального состояния покоя?
Дано Решение
М=1 кг Будем считать систему, связанную с наклонной плоскостью
α=30 0 инерциальной. Для первого тела по 2 закону Ньютона
μ=0,3 ОХ: T1-Fтр-Mgsinα=0
m max-? Оу: N-Mgcosα=0

Для второго тела 2 закон Ньютона:
Оу: mg-T2=0. Т2=mg, Т1=Т2=Т. Fтр ≤μN.
57 слайд

Задача.
Грузы массами М =1 кг и m связаны лёгкой нерастяжимой
нитью, переброшенной через блок, по которому нить может
скользить без трения. Груз массой М находится на
шероховатой наклонной плоскости ( угол наклона плоскости
к горизонту 30 градусов, коэффициент трения 0,3). Чему
равно максимальное значение массы m, при которой система
грузов ещё не выходит из первоначального состояния покоя?
Дано Решение
М=1 кг Будем считать систему, связанную с наклонной плоскостью
α=30 0 инерциальной. Для первого тела по 2 закону Ньютона
μ=0,3 ОХ: T1-Fтр-Mgsinα=0
m max-? Оу: N-Mgcosα=0

Для второго тела 2 закон Ньютона:
Оу: mg-T2=0. Т2=mg, Т1=Т2=Т. Fтр ≤μN.
Fтр =mg -Mgsinα
N=Mgcosα
mg -Mgsinα ≤ μ Mgcosα
m ≤ M(sinα + μ cosα )

m max = M(sinα + μ cosα )=1(0,5+0,3х0,85)=0.76 кг.
Ответ: 0,76 кг
58 слайд

Задача.
При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н. На краю трамплина скорость
гонщика направлена под таким углом к
горизонту, что дальность его полёта
максимальна. Пролетев по воздуху, гонщик
приземлился на горизонтальный стол,
находящийся на той же высоте, что и край трамплина. Какова высота полёта h на этом трамплине? Сопротивлением воздуха и трением пренебречь.
59 слайд

Задача.
При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н. На краю трамплина скорость
гонщика направлена под таким углом к
горизонту, что дальность его полёта
максимальна. Пролетев по воздуху, гонщик
приземлился на горизонтальный стол,
находящийся на той же высоте, что и край трамплина. Какова высота полёта h на этом трамплине? Сопротивлением воздуха и трением пренебречь.

Решение
1) дальность полёта S=(v2sin2α)/g, высота полёта h= (v2sin2α )/2g
60 слайд

Задача.
При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н. На краю трамплина скорость
гонщика направлена под таким углом к
горизонту, что дальность его полёта
максимальна. Пролетев по воздуху, гонщик
приземлился на горизонтальный стол,
находящийся на той же высоте, что и край трамплина. Какова высота полёта h на этом трамплине? Сопротивлением воздуха и трением пренебречь.

Решение
1) дальность полёта S=(v2sin2α)/g, высота полёта h= (v2sin2α )/2g
2) mv2/2=mgH, H=v2/2g
61 слайд

Задача.
При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н. На краю трамплина скорость
гонщика направлена под таким углом к
горизонту, что дальность его полёта
максимальна. Пролетев по воздуху, гонщик
приземлился на горизонтальный стол,
находящийся на той же высоте, что и край трамплина. Какова высота полёта h на этом трамплине? Сопротивлением воздуха и трением пренебречь.
Решение
1) дальность полёта S=(v2sin2α)/g, высота полёта h= (v2sin2α )/2g
2) mv2/2=mgH, H=v2/2g
3) S максимально, если v2sin2α максимально, т.е. sin2α =1, α =45 0.
h= H sin2α =Hsin45 0=H/2.
Ответ: H/2
62 слайд

Задача.
Два шарика, массы которых отличаются в 3 раза, висят,
соприкасаясь на вертикальных нитях. Лёгкий шарик
отклоняют на угол 90о и отпускают без начальной скорости.
Каким будет отношение кинетических энергий тяжёлого и
лёгкого шариков тотчас после их абсолютно упругого удара?
63 слайд

Два шарика, массы которых отличаются в 3 раза, висят,
соприкасаясь на вертикальных нитях. Лёгкий шарик
отклоняют на угол 90о и отпускают без начальной скорости.
Каким будет отношение кинетических энергий тяжёлого и
лёгкого шариков тотчас после их абсолютно упругого удара?

Решение.
До удара энергией будет обладать только лёгкий шарик, сначала потенциальной Ep = mgh , (где h = длине нити, т. к. угол прямой) а затем кинетической Ek = mυ2/2.
64 слайд

Два шарика, массы которых отличаются в 3 раза, висят,
соприкасаясь на вертикальных нитях. Лёгкий шарик
отклоняют на угол 90о и отпускают без начальной скорости.
Каким будет отношение кинетических энергий тяжёлого и
лёгкого шариков тотчас после их абсолютно упругого удара?

Решение.
До удара энергией будет обладать только лёгкий шарик, сначала потенциальной Ep = mgh , (где h = длине нити, т. к. угол прямой) а затем кинетической Ek = mυ2/2. Т. к. в системе действуют только потенциальные силы, и удар абсолютно упругий, то можно применить и закон сохранения импульса и закон сохранения механической энергии: mυ = mυ1 + 3mυ2, υ2 =( υ — υ1 ) / 3. mυ2 = mυ1 2 + 3mυ22, υ22 = (υ2 — υ1 2) / 3, (υ2 — υ1 2) / 3 =( υ — υ1 )2 / 32, (υ + υ1 ) = (υ — υ1 ) / 3, υ1 = — υ/2. υ2 =( υ+ υ/2 ) / 3 = υ/2.
Для тяжёлого шарика E1 = 3mυ2 /8, для лёгкого E2 = mυ2 /8. E1/ E2 = 3.
65 слайд

.

Брусок массой m кладут на плоскость, наклонённую
под углом α к горизонту, и отпускают с начальной
скоростью равной нулю. Коэффициент трения
между бруском и плоскостью равен μ При каких α
брусок будет съезжать по плоскости? Чему равна при
этом сила трения бруска о плоскость?
66 слайд

.

Брусок массой m кладут на плоскость, наклонённую
под углом α к горизонту, и отпускают с начальной
скоростью равной нулю. Коэффициент трения
между бруском и плоскостью равен μ При каких α
брусок будет съезжать по плоскости? Чему равна
при этом сила трения бруска о плоскость?
Решение.
Запишем второй закон Ньютона в векторной форме
ma=N+Fтр+Fтяж . Выберем оси координат и запишем
это уравнение в проекциях на оси
67 слайд

.

Брусок массой m кладут на плоскость, наклонённую
под углом α к горизонту, и отпускают с начальной
скоростью равной нулю. Коэффициент трения
между бруском и плоскостью равен μ При каких α
брусок будет съезжать по плоскости? Чему равна
при этом сила трения бруска о плоскость?
Решение.
Запишем второй закон Ньютона в векторной форме
ma=N+Fтр+Fтяж . Выберем оси координат и запишем
это уравнение в проекциях на оси
ОХ: maх=-Fтр+Fтяж sin α
ОУ: maу=N-Fтяж cos α
При равномерном скольжении a=0,
Fтр = mgsin α , mgcos α = N,
Fтр = μN = μ mgcos α. mgsin α= μ mgcos α, μ= sinα / cos α = tg α.
α = arctg μ.
Брусок начнёт съезжать с наклонной плоскости при условии α > arctg μ.
Сила трения равна Fтр = μ mgcos α.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 153 749 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

Другие материалы

11.10.2019
324
0

01.10.2019
363
0

Вам будут интересны эти курсы:

Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»
Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС педагогических направлений подготовки»
Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
Курс профессиональной переподготовки «Управление ресурсами информационных технологий»
Курс повышения квалификации «Методы и инструменты современного моделирования»
Курс профессиональной переподготовки «Управление сервисами информационных технологий»
Курс повышения квалификации «Актуальные вопросы банковской деятельности»
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»
Курс профессиональной переподготовки «Организация и управление службой рекламы и PR»
Курс профессиональной переподготовки «Организация и управление процессом по предоставлению услуг по кредитному брокериджу»
Курс профессиональной переподготовки «Технический контроль и техническая подготовка сварочного процесса»
Курс профессиональной переподготовки «Стратегическое управление деятельностью по дистанционному информационно-справочному обслуживанию»

Источник

Презентация «Законы сохранения в механике » составлена в соответствии с требованиями к ЕГЭ по физике 2013 года и предназначена для подготовки выпускников к экзамену. Состоит из теоретической и практической части

Скачать:

Подписи к слайдам:

Подготовка к ЕГЭЗаконы сохранения в механике часть 1 Учитель физики Тычкова Н.А.МБОУ СОШ № 91Г. Красноярск Импульс тела
Закон сохранения импульса В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.Нецентральное соударение шаров разных масс: 1 – импульсы до соударения; 2 – импульсы после соударения; 3 – диаграмма импульсов
Импульс силы – временная характеристика действия силы Абсолютно упругий удар (тело отскакивает с прежней по величине скоростью).
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело. Работа силы Работой A, совершаемой постоянной силой называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы и перемещения A = Fs cos αРабота является скалярной величиной. Она может быть положительной (0° ≤ α < 90°), отрицательной (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю. В системе СИ работа измеряется в джоулях (Дж);Графически работа определяется по площади криволинейной фигуры под графиком Fs(x)Работа всех приложенных сил равна работе равнодействующей силы F. Кинетическая энергия тела массой m, движущегося со скоростью V, равна работе, которую должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.
Теорема о кинетической энергии: работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии:
Кинетическая энергия Потенциальная энергия Кинетическая энергия – это энергия движения. Потенциальная энергия — энергии взаимодействия телПотенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Силы, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями называются консервативными.Работа консервативных сил на замкнутой траектории равна нулю. A = A1a2 + A2b1 = A1a2 – A1b2 = 0Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.Сила трения не является консервативной. Работа силы трения зависит от длины пути

Подписи к слайдам:

Подготовка к ЕГЭЗаконы сохранения в механике часть 3 Учитель физики Тычкова Н.А.МБОУ СОШ № 91Г. Красноярск РЕШЕНИЕ ЗАДАЧ1. Система состоит из двух тел a и b. На рисунке стрелками в заданном масштабе указаны импульсы этих тел. Чему по модулю равен импульс всей системы?1) 4 кг м/с 2) 8 кг м/с 3) 5,7 кг м/с 4) 11.7 кг м/с 2. Система состоит из двух тел 1 и 2, массы которых равны 0,5 кг и 2 кг. На рисунке стрелками в заданном масштабе указаны скорости этих тел.Чему равен импульс всей системы по модулю?1) 14 кг м/с 2) 10 кг м/с 3) 20 кг м/с 4) 40 кг м/с 3. Если при увеличении модуля скорости материальной точки величина ее импульс увеличилась в 4 раза, то при этом кинетическая энергия1) увеличилась в 2 раза2) увеличилась в 4 раза3) увеличилась в 16 раз4) уменьшилась в 4 раза 4. Танк движется со скоростью , а грузовик со скоростью . Масса танка . Отношение величины импульса танка к величине импульса грузовика равно 2,25. Масса грузовика равна 1) 1 500 кг 2) 3 000 кг 3) 4 000 кг 4) 8 000 кг 5. Две тележки движутся навстречу друг другу с одинаковыми по модулю скоростями . Массы тележек m и 2m. Какой будет скорость движения тележек после их абсолютно неупругого столкновения? 2/3v 3v 2v1/3v 6. Охотник массой 60 кг, стоящий на гладком льду, стреляет из ружья в горизонтальном направлении. Масса заряда 0,03 кг. Скорость дробинок при выстреле 300 м/с . Какова скорость охотника после выстрела?0.5 м/с0.15 м/с0.3 м/с3 м/с ДЕМО 2013
ДЕМО 2011 ДЕМО 2012 Уровень С. ЕГЭ 2008 г Решите самостоятельно Решите самостоятельно Литература http://physics.kgsu.ru/index.php?option=com_content&view=article&id=129&Itemid=72http://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D1%89%D0%BD%D0%BE%D1%81%D1%82%D1%8Chttp://www.alleng.ru/edu/phys3.htmhttp://www.alsak.ru/content/view/200/1/http://www.physics.ru/courses/op25part1/content/chapter1/section/paragraph19/theory.htmlhttp://fipi.ru/view/sections/92/docs/http://www.vixri.ru/d/Kas’janov%20A.V.%20%20_10%20klass.%20Illjustrirovannyj%20Atlas%20po%20fizike.pdfМякишев, Г.Я. и др. Физика. 11 класс [Текст]: учебник для общеобразовательных школ / учебник для общеобразовательных школ Г.Я. Мякишев, Б.Б. Буховцев . –» Просвещение «, 2009. ФИПИ ЕГЭ 2012 Физика Типовые экзаменационные задания Под редакцией М.Ю.Демидовой, Москва Национальное образование 2011

Подписи к слайдам:

Мощность
Мощность N это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа: Международной системе (СИ) единица мощности называется ватт (Вт)
Закон сохранения механической энергии Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.Ek1 + Ep1 = Ek2 + Ep2. Сумму E = Ek + Ep называют полной механической энергиейЕсли между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).Закон сохранения и превращения энергии: при любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Работа как мера изменения энергии Работа силы тяжести:Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести. Работа этой силы зависит только от вертикального перемещения тела. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком. A = – (Eр2 – Eр1). Работа силы тяжести не зависит от формы траекторииРабота силы тяжести не зависит от выбора нулевого уровня. Работа силы упругости:Для того, чтобы растянуть пружину, к ней нужно приложить внешнюю силу модуль которой пропорционален удлинению пружины Зависимость модуля внешней силы от координаты x изображается на графике прямой линиейПотенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.

По теме: методические разработки, презентации и конспекты

Открытый урок: «Законы сохранения в механике».

Данный урок дан в рамках методического дня. Урок рассчитан на 90минут. Часто учителя работающие в 10-ых классах не выполняют лабораторную работу по данной теме, потому что она не всегда получается. Ур…

Мне нравится

Источник

1. Механика

Подготовка к ЕГЭ

2. Из теории вопроса

Законы Ньютона

3. Первый закон Ньютона

Существуют такие системы отсчета,
относительно которых
материальная точка сохраняет свое
состояние покоя или равномерного
прямолинейного движения до тех
пор, пока на нее не действуют
другие тела или их действие
компенсируется.

4. Основная модель – материальная точка.

СО, в которой материальная точка
в отсутствие воздействия со
стороны других тел движется с
постоянной скоростью или
покоится, называется
ИНЕРЦИАЛЬНОЙ.
Законы Ньютона справедливы
только в инерциальных системах
отсчета

5. ИНСО

Как показывают наблюдения,
инерциальной можно считать СО,
связанную с Землей.
Любая СО, движущаяся
равномерно и прямолинейно
относительно инерциальной
системы, также является
инерциальной

6. Второй закон Ньютона

Равнодействующая всех сил,
приложенных к телу, равна
произведению массы этого тела на
ускорение, сообщаемое этой силой.

7. Движение и силы

Направление ускорения всегда
совпадает с направлением
равнодействующей силы.
Под действием постоянной силы
тело движется равноускоренно.
Коэффициентом
пропорциональности между силой
и ускорением является масса тела мера его инертности

8. Третий закон Ньютона

Тела действуют друг на друга
силами одинаковой природы,
равными по величине и
направленными в
противоположные стороны.

9. Невесомая нерастяжимая нить

«Невесомость» нити позволяет не
рассматривать ее как отдельное тело и
значит не писать для нее основное
уравнение динамики. Поэтому, силы
реакции нити, приложенные к
связанным телам, оказываются равными
по модулю.
Условие «нерастяжимости» позволяет
считать, что все связанные тела
движутся с одинаковыми ускорениями.

10. Наклонная плоскость

Характеризуется
Линейными размерами: высота –h
Длина — s , длина основания – l
Углом при основании
Углом при вершине
Углом наклона

11. Обозначая на схеме силы,

Сила тяжести всегда направлена
вертикально вниз, по ускорению
свободного падения
Сила упругости направлена против
смещения тел при деформации,
возникает в деформированном
теле, но приложена к тому объекту
действием которого вызвана
деформация.

12. Сила- векторная величина.

Сила трения скольжения всегда
направлена против движения, а
сила трения покоя – против
возможного движения.
Сила нормального давления
направлена перпендикулярно
поверхности.
Сила Архимеда всегда направлена
вертикально вверх

13. Решение динамических задач

Всегда строится на векторной
записи второго закона Ньютона.
При этом часто приходится
вспоминать основные уравнения
кинематики.

14. Алгоритм решения задач с использованием 2 закона.

Нарисуйте рисунок с указанием
всех сил, действующих на тело, а
также скорости и ускорения.
Выберите инерциальную СО
Напишите второй закон Ньютона в
векторном виде
Напишите второй закон в
проекциях на выбранные оси

15. Алгоритм решения задач

В случае необходимости дополните
получившуюся систему уравнений
формулой для вычисления силы
трения.
Решите получившуюся систему
уравнений относительно искомой
величины, выполните расчет,
проверьте результат на «здравый
смысл»

16. Задания части А

Тело массой 3 кг
покоится на
наклонной плоскости
с углом при
основании 30 град.
Определите величину
силы трения покоя.
Коэффициент трения
0,1.
В отличии от силы
трения скольжения,
сила трения покоя
саморегулируется и в
зависимости от
внешнего
воздействия
колеблется от 0 до
некоторого
максимума,
подчиняется
уравнению F=kN

17. Часть А

Тело массой 3 кг
соскальзывает вниз
по наклонной
плоскости с углом
при основании 30
град. Определите
величину силы
трения,
действующую на
тело. Коэффициент
трения 0.1.
При движении на
тело действует сила
трения,
направленная в
сторону
противоположную
движению.
При решении задачи
необходимо
воспользоваться
стандартным
алгоритмом решения
задач по динамике.

18. Часть А

Тело скользит по
наклонной плоскости
с ускорением равным
0.6g. Во сколько раз
возрастет ускорение
тела при увеличении
угла наклона
плоскости в 2 раза?
Примените алгоритм
решения задач
последовательно для
обоих случаев,
выразив ускорение.
Используйте
калькулятор или
таблицу Брадиса для
нахождения угла
наклона по его
синусу.

19. Часть А

Сани с седоками общей
массой 100 кг начинают
съезжать с горы высотой
8 м и длиной 100
м.Какова средняя сила
сопротивления движению
санок, если в конце горы
они достигают скорости
10 м/с?
Используя алгоритм
динамики, можно
определить ускорение с
которым спускаются
сани.
Зная ускорение. массу
тела и вычислив угол
наклона горы через ее
высоту и длину, можно
найти среднюю силу
трения.
Энергетический подход в
этой задаче дает
КОРОТКОЕ И
РАЦИОНАЛЬНОЕ решение

20. Часть С

Мальчик на санках общей массой
60 кг спускается с горы и
останавливается, проехав 40 м по
горизонтальному участку дороги
после спуска. Какова высота горы,
если сила сопротивления
движению на горизонтали равна 60
Н? Считать, что по склону горы
сани скользили без трения.

21. Подсказки для решения задачи.

Мальчик последовательно
участвует в двух видах движения:
ускоренный спуск с горы с
ускорением а1 и замедленное
движение по горизонтали с
ускорением а2.
Пользуясь алгоритмом динамики
необходимо рассмотреть обе
ситуации.

22. Подсказки для решения задачи

Зная величину тормозного пути при
движении по горизонтали, можно
вычислить скорость, которую набрали
сани при спуске.
Начальная скорость на горизонтальном
участке является конечной для спуска с
горы.
Высота горы может быть найдена на
основании закона сохранения энергии.

Источник

Решение задач из ЕГЭ часть С «Механика»

Никифорова Наталья Владиленовна,

учитель физики МБУ «Лицей №51» г.о. Тольятти

ЗАДАЧА № 1

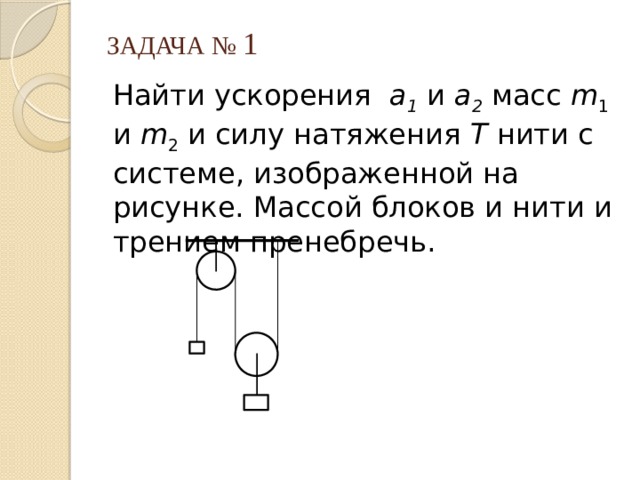
Найти ускорения a 1 и a 2 масс m 1 и m 2 и силу натяжения Т нити с системе, изображенной на рисунке. Массой блоков и нити и трением пренебречь.

РЕШЕНИЕ:

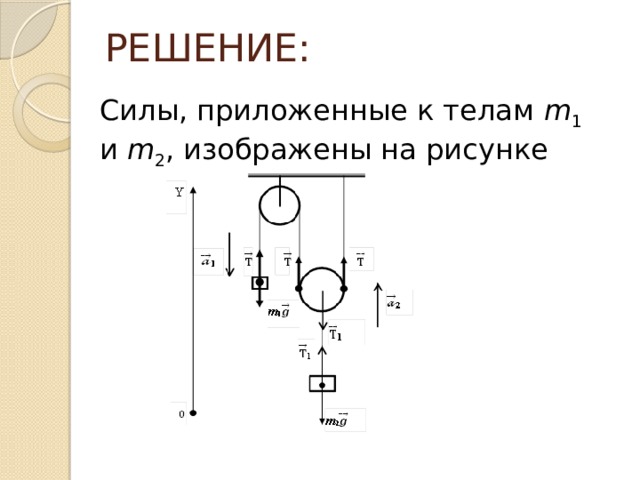
Силы, приложенные к телам m 1 и m 2 , изображены на рисунке

РЕШЕНИЕ:

Предполагая, что ускорения тел a 1 и a 2 направлены, как показано на рисунке, введем ось координат 0Y и запишем второй закон Ньютона.

Т – m 1 g = – m 1 a 1 , (1)

T 1 – m 2 g = m 2 a 2 . (2)

Запишем второй закон Ньютона для подвижного блока (массой блока можно пренебречь):

T 1 – 2Т = 0 , следовательно:

T 1 = 2Т.

РЕШЕНИЕ:

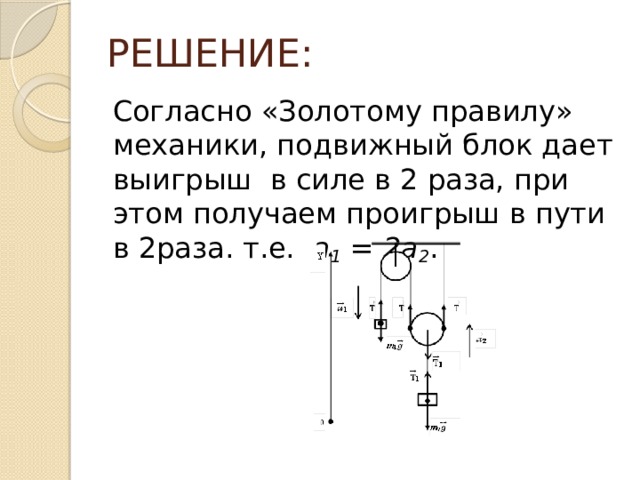
Согласно «Золотому правилу» механики, подвижный блок дает выигрыш в силе в 2 раза, при этом получаем проигрыш в пути в 2раза. т.е. a 1 = 2a 2 .

РЕШЕНИЕ:

Из уравнения (1) выразим Т

Т= m 1 g – m 1 a 1 . (4)

Из уравнения (2) выразим T 1

T 1 = m 2 g + m 2 a 2 , с учетом T 1 = 2Т получим

2T = m 2 g + m 2 a 2 . (5) Подставим формулу (3) a 1 = 2a 2 в (4):

Т= m 1 g – 2m 1 a 2 . (6)

Подставим формулу (6) в (5) и выразим a 2 :

2 ( m 1 g – 2m 1 a 2 ) = m 2 g + m 2 a 2 ,

a 2 = g ( 2m 1 – m 2 ) / (4 m 1 + m 2 ).

РЕШЕНИЕ:

Найдем a 1 = 2a 2 ,

a 1 = 2g ( 2m 1 – m 2 ) / (4 m 1 + m 2 ). (7)

Подставим формулу (7) в (4) и выразим Т :

Т = 3g m 1 m 2 / (4 m 1 + m 2 ).

Ответ: a 1 = 2g ( 2m 1 – m 2 ) / (4 m 1 + m 2 ),

a 2 = g ( 2m 1 – m 2 ) / (4 m 1 + m 2 ),

Т = 3g m 1 m 2 / (4 m 1 + m 2 ).

ЗАДАЧА № 2

Маленькое тело соскальзывает с нулевой начальной скоростью по внутренней поверхности полусферы с высоты, равной ее радиусу. Одна половина полусферы абсолютно гладкая, а другая — шероховатая, причем на этой половине коэффициент трения между телом и поверхностью μ = 0,15. Определить величину ускорения а тела в тот момент, когда оно перейдет на шероховатую поверхность. Ускорение свободного падения принять равным g = 10 м/с 2 .

РЕШЕНИЕ:

Изобразим силы, действующие на тело в момент, когда оно оказывается на шероховатой поверхности.

Ускорение тела а в рассматриваемый момент времени равно: =+.

а τ — касательное ускорение, направлено по касательной к траектории движения тела, а n — нормальное ускорение тела, направлено по радиусу к центру окружности.

РЕШЕНИЕ:

Введем систему координат, запишем второй закон Ньютона m + + m ,

и спроецируем его на оси 0Y и 0Х :

ma n = N – mg, (1)

ma τ = F тp . (2)

Поскольку a n =υ 2 /R, где υ — скорость тела, из уравнения (1) следует, что

N = ( mυ 2 /R ) + mg .

Сила трения равна

F тp = μN, F тp = μm(g + υ 2 /R) . (3)

РЕШЕНИЕ:

Подставляем (3) в (2), получаем

a τ = μ (g + υ 2 /R) (4)

При движении тела по гладкой поверхности справедлив закон сохранения энергии :

mυ 2 /2 = mgR,

Из него υ 2 = 2gR.

Из (4) получаем a τ =3μg; для a n =υ 2 /R, a n =2g.

Находим ускорение тела по формуле

a=(a τ 2 + а n 2 ) 1/2

Ответ: a= g (9 μ 2 + 4) ½ = 20,5 м/с 2

ЗАДАЧА № 3

К одному концу лёгкой пружины жёсткостью к = 100 Н/м прикреплён груз массой m = 1 кг, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно. Коэффициент трения груза по плоскости μ = 0,2. Груз смещают по горизонтали, растягивая пружину на величину d , затем отпускают с начальной скоростью, равной нулю. Найдите максимальное значение d , при котором груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата.

РЕШЕНИЕ:

Начальная энергия системы равна потенциальной энергии растянутой пружины: W 1 = k d 2 /2. После того, как пружину отпустили, она остановится в положении, при котором она сжата на величину x . Тогда конечная энергия системы равна потенциальной энергии сжатой пружины: W 2 = k x 2 /2.

Изменение полной энергии системы равно работе силы трения:

W 2 — W 1 = А тр ,

А тр = F тр ( d + x ) cos 180° = – F тр ( d + x ), F тр = μN,

k /2 ( x 2 – d 2 ) = – μN ( d + x ), k /2 ( d 2 – x 2 ) = μN ( d + x ),

k /2 ( d – x ) = μN . (1)

РЕШЕНИЕ:

Для момента, когда груз остановился, запишем второй закон Ньютона для оси OY и OX:

N — mg = 0 , N= mg (2)

F у – F тр = 0, k x = μN (3)

Подставим (2) в (3) и выразим x :

x = μmg/ k. (4)

Подставим формулы (2) и (4) в k /2 ( d – x ) = μN :

k /2 ( d – μmg/ k ) = μmg , kd /2 = μmg + μmg/ 2,

kd = 3 μmg , d = 3 μmg/ k.

Ответ: d = 6 см .

ЗАДАЧА № 4

Грузовой автомобиль массой М = 4 т с двумя ведущими осями тянет за нерастяжимый трос вверх по склону легковой автомобиль массой m = 1 т, у которого выключен двигатель. С каким максимальным ускорением могут двигаться автомобили, если угол наклона составляет α = arcsin 0,1, а коэффициент трения между шинами грузового автомобиля и дорогой μ = 0,2? Силой трения качения, действующей на легковой автомобиль, пренебречь. Массой колес пренебречь.

РЕШЕНИЕ:

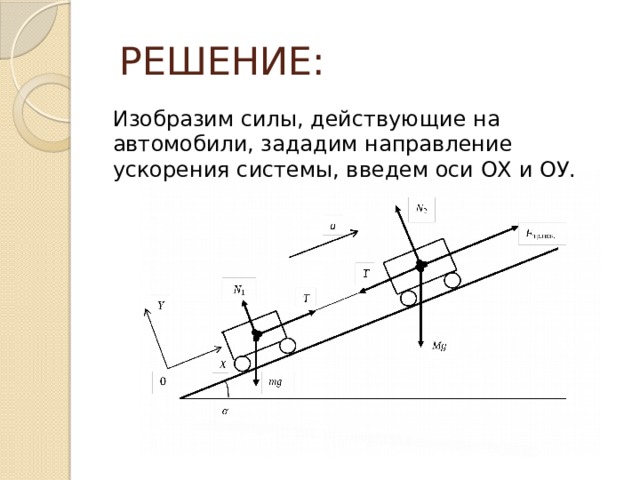
Изобразим силы, действующие на автомобили, зададим направление ускорения системы, введем оси ОХ и ОУ.

РЕШЕНИЕ:

Запишем уравнение второго закона Ньютона для грузового автомобиля в проекции на ось ОХ:

F тр.пок – Мg sinα – T = Ma , (1)

в проекции на ось ОУ:

N 2 – Мg cosα = 0 , отсюда N 2 = Мg cosα .

Максимальная сила трения покоя, действующая на грузовой автомобиль (сила сцепления колес с дорогой) равна:

( F тр.пок ) мах = μ N 2 = μМg cosα . (2)

РЕШЕНИЕ:

Запишем второй закон Ньютона для легкового автомобиля в проекции на ось ОХ:

Т – mg sinα = ma , отсюда

Т = m ( g sinα + a ). (3)

Подставим формулы (2) и (3) в (1):

μМg cosα – Мg sinα – m ( g sinα + a ) = Ma ,

и выразим ускорение автомобилей

a = ( Мg ( μ cosα – sinα ) – mg sinα ) / ( M + m ).

Получим численное значение ускорения

a = 0,6 м/с 2 .

Ответ: a = 0,6 м/с 2 .

Список литературы

ЕГЭ 2010. Физика: сборник экзаменационных заданий/ Авт.-сост. М.Ю.Демидова, И.И. Нурминский. – М.: Эксмо, 2010.
Отличник ЕГЭ. Физика. Решение сложных задач. под ред. В.А. Макарова, М.В. Семенова, А.А. Якуты; ФИПИ. – М.: Интеллект-Центр, 2010.
Савченко Н.Е. Задачи по физике с анализом их решения. – М.: Просвещение: Учеб. лит., 1996.

Благодарю за внимание!

Источник

1

Материал для подготовки к ЕГЭ по физике «Механика» Учитель физики МОУ СОШ 7 г. Балашова Телкова И. В.

2

Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения. Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени. Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени. Тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой. Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела. Перемещением тела S называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина. Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина. Простейшим видом механического движения является движение тела вдоль прямой линии с постоянной по модулю и направлению скоростью. Такое движение называется равномерным. Средняя и мгновенная скорости прямолинейного неравномерного движения. Движение, при котором за равные промежутки времени тело совершает неравные перемещения, называют неравномерным (или переменным). При переменном движении скорость тела с течением времени изменяется, поэтому для характеристики такого движения введены понятия средней и мгновенной скоростей. Средней скоростью переменного движения v cp называют векторную величину, равную отношению перемещения тела s к промежутку времени t, за который было совершено это перемещение: v cp =s/t. Средняя скорость характеризует переменное движение в течение только того промежутка времени, для которого эта скорость определена. Зная среднюю скорость за данный промежуток времени, можно определить перемещение тела по формуле s=v ср ·t лишь за указанный промежуток времени. Мгновенной скоростью переменного движения называют скорость, которую тело имеет в данный момент времени (и следовательно, в данной Равноускоренным движением называют такое движение, при котором вектор ускорения. Равноускоренное движение остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения g. точке траектории). Движение, происходящее по криволинейной траектории, называют криволинейным. Частным случаем криволинейного движения является движение по окружности. Механика

3

Явление Графическая модель Законы Равномерное движение Зависимость координаты x от времени t (закон движения) выражается при равномерном прямолинейном движении линейным математическим уравнением V S X 0 S x X X Для закона движения, изображенного на графике I, при t = 0 тело находилось в точке с координатой x 0 = –3. Между моментами времени t 1 = 4 с и t 2 = 6 с тело переместилось от точки x 1 = 3 м до точки x 2 = 6 м. Таким образом, за Δt = t 2 – t 1 = 2 с тело переместилось на Δs = x 2 – x 1 = 3 м. Следовательно, скорость тела составляет v=1,5 м/с; x(t) = ,5t. Δs = x 2 – x 1 x(t) = x 0 + υt. Система знаний по кинематике: S t x t V t

4

Равноускоренным движением называют такое движение, при котором вектор ускорения остается неизменным по модулю и направлению. a V S X 1 S x X 0 X По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. для графика I. Ускорение численно равно отношению сторон треугольника АВС: Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела. Для графика I: υ 0 = –2 м/с, a = 1/2 м/с 2 ; S = -2t+1/4t 2 Для графика II: υ 0 = 3 м/с, a = –1/3 м/с 2 ; S = 3t-1/6t 2 Движение тела по окружности является частным случаем криволинейного движения. При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора

5

Основные понятия: Динамика рассматривает действие одних тел на другие как причину, определяющую характер движения тел. Первый закон Ньютона (или закон инерции) из всего многообразия систем отсчета выделяет класс так называемых инерциальных систем. Примером тонкого механического эксперимента, в котором проявляется неинерциальность системы, связанной с Землей, служит поведение маятника Фуко. Причиной изменения скорости движения тела в инерциальной системе отсчета всегда является его взаимодействие с другими телами. Для количественного описания движения тела под воздействием других тел необходимо ввести две новые физические величины – инертную массу тела и силу. Масса – это свойство тела, характеризующее его инертность. Масса тела – скалярная величина. Опыт показывает, что если два тела с массами m 1 и m 2 соединить в одно, то масса m составного тела оказывается равной сумме масс m 1 и m 2 этих тел: m = m 1 + m 2. Это свойство масс называют аддитивностью. Сила – это количественная мера взаимодействия тел. Сила является векторной величиной. На практике нет необходимости все измеряемые силы сравнивать с эталоном силы. Для измерения сил используют пружины, откалиброванные описанным выше способом. Такие откалиброванные пружины называются динамометрами. Сила измеряется по растяжению динамометром. Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение: Это равенство называется третьим законом Ньютона. Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению. Динамика

6

Сила Определение, формула Рисунок Сила всемирного тяготения Закон всемирного тяготения был открыт И. Ньютоном в 1682 году. Еще в 1665 году 23-летний Ньютон высказал предположение, что силы, удерживающие Луну на ее орбите, той же природы, что и силы, заставляющие яблоко падать на Землю. По его гипотезе между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей центры масс. У тела в виде однородного шара центр масс совпадает с центром шара. Гравитационная постоянная G = 6,67·10–11 Н·м 2/кг 2 (СИ). g – ускорение свободного падения у поверхности Земли:

7

Вес, сила реакции опоры Весом тела называют силу, с которой тело вследствие его притяжения к Земле действует на опору или подвес. Силу называют силой нормального давления или силой реакции опоры. В соответствии с третьим законом Ньютона тело действует на опору с некоторой силой равной по модулю силе реакции опоры и направленной в противоположную сторону: Вес тела и сила тяжести. – сила тяжести, – сила реакции опоры, – сила давления тела на опору (вес тела). Сила упругости При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости Fx = Fупр = –kx Сила трения Трение – один из видов взаимодействия тел. Оно возникает при соприкосновении двух тел. Трение, как и все другие виды взаимодействия, подчиняется третьему закону Ньютона: если на одно из тел действует сила трения, то такая же по модулю, но направленная в противоположную сторону сила действует и на второе тело. Силы трения, как и упругие силы, имеют электромагнитную природу. Они возникают вследствие взаимодействия между атомами и молекулами соприкасающихся тел. F тр = (F тр ) max = μN.

8

Статикой называется раздел механики, изучающий условия равновесия тел. Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю. Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю: M 1 + M = 0. Условия равновесия я шара на опоре. (1) – безразличное равновесие, (2) – неустойчивое равновесие, (3) – устойчивое равновесие.

10

Рычагом называют твёрдое тело, которое может вращаться вокруг некоторой оси. Рычаг – это не обязательно длинный и тонкий предмет. Например, рычагом является любое колесо, так как оно может вращаться вокруг оси. Введём два определения. Линией действия силы назовём прямую, проходящую через вектор силы. Плечом силы назовём кратчайшее расстояние от оси рычага до линии действия силы. Из геометрии вы знаете, что кратчайшее расстояние от точки до прямой – это расстояние по перпендикуляру к прямой. При помощи рычага можно маленькой силой уравновесить большую силу. Рассмотрим, например, подъём ведра из колодца. Рычагом является колодезный ворот – бревно с прикреплённой к нему изогнутой ручкой. Ось вращения ворота проходит сквозь бревно. Меньшей силой служит сила руки человека, а большей силой – сила, с которой цепь тянет вниз

13

Задачи: 1. Поезд массой m=3·10 6 кг движется с начальной скоростью v= 40 км/ч. Определить среднюю силу торможения, если поезд останавливается за время t=1 мин 20 с. 2. Под действием какой силы тяги автомобиль массой m=3 т будет двигаться: 1) равномерно, 2) с ускорением а = 1 м/с 2 ? Принять силу трения, равной 0,1 веса автомобиля. 3. Стальной трос подъемного крана выдерживает силу натяжения Т = 5 кН. Какой максимальный груз он может поднять с ускорением а=1,5 м/с 2 ? 4. Гусеничный трактор тянет за собой прицеп по снегу па полозьях. Определить силу F тяги на крюке трактора, если он движется с ускорением а = 1,84 м/с 2. Коэффициент трения полозьев о снег µ=0,06. Масса прицепа m=3 т. (7,3 кН) 5. Определить скорость вагона массой m=25 т к началу торможения, если он останавливается за время t=2 мин под действием силы трения F=4 кН. (19,2 м/с) 6. Определить ускорение а, которое сообщает вагону сила F =90 кН. Масса вагона m=18 т. Коэффициент трения k=0,05. (4,5 м/с 2) 7. Определить силу натяжения Т каната при подъеме лифта массой m=1500 кг с ускорением а=1,8 м/с 2. (17,4 кН) 8. Вагон движется равнозамедленно с ускорением а=-0,5 м/с 2. Начальная скорость вагона v=54 км/ч. Через сколько времени вагон остановится и какой путь пройдет до остановки? (30 с; 225 м) 9. Стальная проволока выдерживает силу натяжения T=4,4 кН. С каким наибольшим ускорением можно поднять груз массой m=390 кг, подвешенный на этой проволоке, чтобы она при этом не разорвалась. (1,46 м/с 2) 10. Определить скорость, которую получит поезд через t=30 с после начала движения, если коэффициент трения k=0,02. Масса поезда m=5·10 6 кг, сила тяги паровоза F=1,65 МН. (4,02 м/с) 11. Электротрактор движется со скоростью м=6,28 км/ч. Какой путь пройдет трактор до полной остановки после выключения двигателя, если сила сопротивления составляет 0,3 силы тяжести. (0,52 м) 12. Определить силу тяги на крюке трактора, если ускорение, с которым трактор ведет прицеп, а= 0,2 м/с 2. Масса прицепа m= 0,5 т, сопротивление движению F=1,5 кН. (1,6 кН) 13. Перпендикулярно к стенке сосуда летит частица массой m=4, кг со скоростью υ=600 м/с. Определить импульс, полученный стенкой при упругом соударении частицы. (5, Нс) 14. Шарик массой m=200 г, двигаясь горизонтально, ударился о стенку и при этом сообщил ей импульс силы I = Ft=4 Нс. Определить скорость шарика в момент удара. Удар считать абсолютно упругим. (10 м/с). 15. Определить силу тяготения двух соприкасающихся медных шаров радиусом R=1 м каждый. Плотность меди ρ =8,910 3 кг/м 3. (23,1 мН) 16. Определить ускорение свободного падения тел на Луне. Принять радиус Луны Rл= 1740 км, массу ее m=7, кг. (1,61 м/c 2 )

14

Полезные ссылки

Источник

: ЕГЭ по физике

Презентация для подготовки к ЕГЭ по физике на тему: «Задачи по механике».

Представлены подробные решения задач.

→ скачать презентацию

Примеры задач:

Задача 1.

Можно ли принять Землю за материальную точку при расчете:

а) расстояния от Земли до Солнца;

б) пути, пройденного Землей по орбите вокруг Солнца за месяц;

в) длины экватора;

г) скорости движения Земли по орбите вокруг Солнца?

Задача 3.

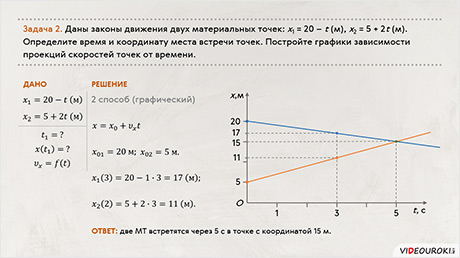
Даны законы движения двух материальных точек: x1 = 20 – t (м), x2 = 5 + 2t (м). Определите время и координату места встречи точек. Постройте графики зависимости проекций скоростей точек от времени.

Задача 4.

Две материальные точки движутся равномерно вдоль координатных осей х и у так, как это показано на рисунке. Определите расстояние между точками в начале движения, если через 2,5 с они одновременно проходят начало координат. Чему равен модуль скорости второй точки относительно первой, если скорость первой точки равна 1,8 м/с, а второй — 3,2 м/с?

Задача 7.

Локомотив, уравнение движения которого имеет вид x = A + Bt + Ct 2, где А = -500 м,

В = 15 м/с, С = −0,1 м/с2, начинает тормозить перед светофором. Определите: а) положение локомотива через 60 с; б) время торможения и положение локомотива при остановке; в) положение локомотива через 300 с после начала торможения.

Связанные страницы:

Источник

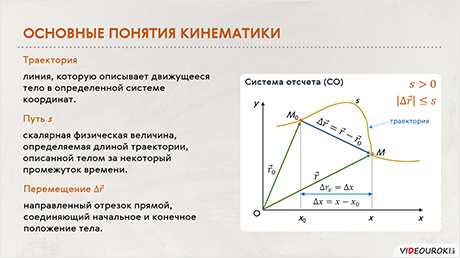
Урок 1. Основные понятия кинематики. Относительность движения

Мы приступаем к повторению первого раздела физики, который называется «Кинематика». И на первом уроке вспомним, какой раздел физики называется кинематикой, поговорим о механическом движении тел и способах его описания. А также разберемся с понятием относительности механического движения.

Урок 2. Основные понятия кинематики. Относительность движения (практика)

Как известно, для описания движения тела необходимо выбрать тело отсчета и связать с ним систему координат. В качестве тела отсчета может выступать любое тело. Однако в различных системах отсчета будут различны вид траектории, значения скорости, перемещения и других величин. На этом уроке мы рассмотрим решение нескольких таких задач. Покажем вариативность выбора систем отсчета и удобства их применения в различных случаях.

Урок 3. Равномерное прямолинейное движение. Скорость

На этом занятии мы с вами еще раз повторим некоторые важные понятия кинематики. Поговорим о равномерном прямолинейном движении тел и способах описания такого движения. Еще раз затронем относительность движения и выведем классический закон сложения скоростей.

Урок 4. Равномерное прямолинейное движение. Скорость (практика)

В школе знакомство с равномерным прямолинейным движением происходит еще на уроках математики 3 — 4 класса. Однако более углубленное изучение этой темы начинается на уроках физики. На данном уроке мы рассмотрим решение задач на РПД. Покажем уместность использования графического метода решения задач в сравнении со стандартным аналитическим методом.

Урок 5. Равноускоренное прямолинейное движение. Ускорение

На этом уроке мы вспомним, какое движение называется равноускоренным. Повторим формулы для определения скорости тела, его координаты, пути и перемещения при равноускоренном движении. А также рассмотрим графическое представление зависимости кинематических величин от времени при таком движении.

Урок 6. Равноускоренное прямолинейное движение. Ускорение (практика)

В этом видеоуроке мы продолжим рассматривать равноускоренное движение тел. Вашему вниманию предлагается решение трех задач на данную тему. Однако мы постарались показать всевозможные варианты их решений. Вы можете самостоятельно выбрать тот, который Вы хотели бы продемонстрировать на конкретном занятии. А можете показать их в сравнении.

Урок 7. Свободное падение. Ускорение свободного падения

Посмотрев данный видеофрагмент, мы выясним, какое движение называют свободным падением. Вспомним, что ускорение, с которым движется тело во время свободного падения называют ускорением свободного падения и повторим, как можно рассчитать это ускорение. А также рассмотрим виды наиболее часто встречающихся движений тел под действием силы тяжести — это свободное падение тел по прямолинейной и криволинейной траектории.

Урок 8. Свободное падение. Ускорение свободного падения (практика)

Известно, что решение задач на движение тела только под действием силы тяжести, вызывает достаточные сложности у учащихся. Мы попытались разобрать данный вид движения «по полочкам». В уроке представлено решение трех задач, которые охватывают всевозможные моменты движения тела.

Урок 9. Движение точки по окружности

В видеоуроке мы поговорим о криволинейном движении. Вспомним, что такое движение всегда является ускоренным, так как направление вектора скорости постоянно меняется, даже если её модуль остается постоянным. Вспомним и о том, что ускорение при движении по окружности направленно к её центру и поэтому называется центростремительным. Повторим некоторые важные физические величины, описывающие криволинейное движение. А также поговорим о движении твердых тел.

Урок 10. Движение точки по окружности (практика)

В данном видеофрагменте мы рассмотрим решение задач на равномерное движение тела по окружности. Первые три из них предлагают вспомнить основные формулы по данной теме. Четвертая задача — это классическая задача на вращение связанных тел. Ее решение представлено двумя способами — математическим и физическим. В задаче №5 мы разберем сложное движение тела, которое состоит из вращательного и поступательного движений.

Урок 11. ИСО. Первый закон Ньютона

Мы переходим к следующему разделу механики, который называется динамикой. И на этом занятии мы с вами вспомним, какой раздел физики называют динамикой и какова ее основная задача. Повторим формулировку первого закона Ньютона. Поговорим об инерциальных и неинерциальных системах отсчета. А также вспомним, о чем говориться в принципе относительности Галилео Галилея.

Урок 12. Масса и плотность тела

На этом уроке мы вспомним о том, что тело будет двигаться ускоренно в инерциальной системе отсчета, если воздействие других тел на него нескомпенсировано. Выясним, что при взаимодействии двух тел воздействие испытывают оба тела, а отношение модулей ускорений двух взаимодействующих тел равно обратному отношению их масс. А также поговорим о том, как определяется масса тела в классической механике Ньютона.

Урок 13. Первый закон Ньютона. Масса и плотность тела (практика)

Как говорил Карл Линней: «В естественной науке принципы должны подтверждаться наблюдениями». На этом уроке мы разберем решения как качественных, так и количественных задач по данной теме. Естественно, для этого нам понадобятся и знания из кинематики материальной точки.

Урок 14. Сила. Второй и третий законы Ньютона

На этом занятии мы с вами вспомним, что в механике называют силой. Повторим основные формулировки второго и третьего законов Ньютона. А также разберемся с особенностями их применения.

Урок 15. Сила. Второй и третий законы Ньютона (практика)

Динамика (от греческого «сила») — раздел механики, посвященный изучению движения тел под действием приложенных к ним сил. На этом видеоуроке мы рассмотрим решение задач с применением всех трех законов Ньютона, которые были им сформулированы в далеком 1687 году.

Урок 16. Закон всемирного тяготения. Сила тяжести

На этом уроке мы с вами повторим формулировку закона всемирного тяготения, установленного Ньютоном в 1667 году. Вспомним, что называют силой тяжести и ускорением свободного падения. А также поговорим о движении планет и искусственных спутников.

Урок 17. Закон всемирного тяготения. Сила тяжести (практика)

Все тела в природе взаимно притягиваются друг к другу. Впервые Ньютон доказал, что причина, вызывающая падения камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же — это сила всемирного тяготения, действующая между любыми телами во Вселенной. На данном уроке мы попробуем применить знания о силе тяготения для решения различного рода задач, связанных с данной темой.

Урок 18. Сила упругости. Закон Гука

ЭПосмотрев данный видеофрагмент, вы вспомните, какие силы называются силами упругости, какие различают виды деформации тела. Повторим формулировку закона Гука. Вспомним понятие «вес тела», а также рассмотрим его главные отличия от силы тяжести.

Урок 19. Сила упругости. Закон Гука (практика)

На этом занятии мы предлагаем Вам разбор решений задач с использованием закона, экспериментально установленным Робертом Гуком. Разберем решение классической задачи на определения веса тела в ускоренно движущемся лифте.

Урок 20. Силы трения. Коэффициент трения

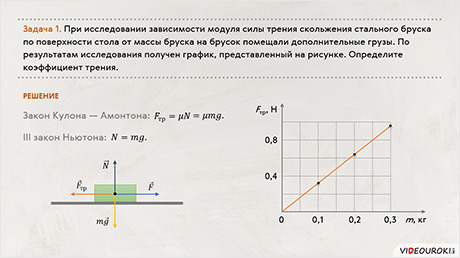
На этом уроке мы вспомним, какие силы называют силами сопротивления. Повторим основные виды сил трения и условия их возникновения. А также вспомнили формулировку закона Кулона — Амонтона.

Урок 21. Силы трения. Коэффициент трения (практика)

Сложность решения задач по этой теме в первую очередь связана с тем, что многие ученики не способны правильно выбрать наилучшую систему координат и определить проекции векторов действующих сил на выбранные оси. В предложенном видеоуроке подробно, шаг за шагом разбираются решения задач по данной теме с рассмотрением правил построения проекций всех сил, действующих на исследуемое тело.

Урок 22. Момент силы. Условия равновесия твёрдого тела

В этом видеофрагменте мы вспоминаем о двух условиях равновесия тел. А также повторяем основные виды равновесия.

Урок 23. Момент силы. Условия равновесия твёрдого тела (практика)

Как говорил известный немецкий ученый Готфрид Вильгельм Лейбниц: «Кто овладел творениями Архимеда, будет меньше удивляться открытиям самых великих людей нашего времени». На этом занятии, при помощи решения задач, мы поймем, почему были сказаны данные слова. Решения некоторых задач потребуют хороших знаний механики Ньютона.

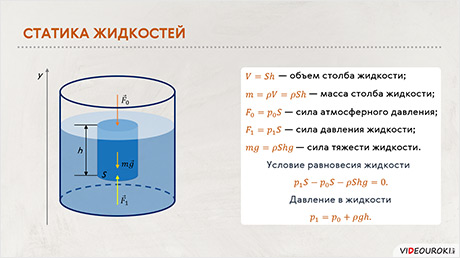
Урок 24. Давление твёрдых тел, жидкостей и газов. Закон Паскаля

На этом занятии мы с вами вспомним основные свойства, которыми обладают жидкости и газы. Повторим понятие «давление» и формулировку закона Паскаля. Поговорим о таком механизме, как гидравлический пресс. А также вспомним, какие сосуды называются сообщающимися и закон, которому подчиняются находящиеся в таких сосудах жидкости.

Урок 25. Давление твёрдых тел, жидкостей и газов. Закон Паскаля (практика)

На этом занятии мы рассмотрим решение нескольких задач на расчет давления и сил давления. В ходе решения задач на определение гидростатического давления, мы научимся различать выражения «давление жидкости на глубине» и «давление в жидкости на глубине».

Урок 26. Закон Архимеда. Условия плавания тел

На этом уроке мы с вами вспомним, какую силу называют выталкивающей и как она возникает. Повторим формулировку закона Архимеда для жидкостей и газов и вспомним классический опыт, подтверждающий данный закон. А также рассмотрим условия плавания тел.

Урок 27. Закон Архимеда. Условия плавания тел (практика)

Главное, что надо помнить при решении некоторых задач на гидростатику, что на все тела, находящиеся в жидкости или газе, действует выталкивающая сила. Поэтому следует не забывать, что вес тела в жидкости — это упругая сила натяжения нити, при этом сила тяжести, приложенная к телу, и вес тела численно не равны.

Урок 28. Импульс. Закон сохранения импульса

В этом видеоуроке мы вспоминаем о том, что называют импульсом тела и импульсом системы. Повторим формулировку одного из фундаментальных законов природы — закона сохранения импульса, и разберемся с областью его применения. А также поговорим о реактивном движении.

Урок 29. Импульс. Закон сохранения импульса (практика)

Казалось бы, что решение задач на закон сохранения импульса не должно вызывать особых проблем у учащихся. Но, как показывает практика, данная тема все же вызывает некоторые затруднения. В первую очередь это связано с тем, что учащиеся не всегда знают, в каких случаях данный закон можно применять, а в каких нет. А также не всегда могут правильно найти проекции вектора импульса на координатные оси. На примере решения конкретных задач мы попытаемся эти пробелы в знаниях устранить.

Урок 30. Механическая работа. Мощность

На этом уроке мы с вами вспомним, какая физическая величина, называется работой. Рассмотрим работу наиболее часто встречающихся сил — силы тяжести, упругости и силы трения. Повторим понятие мощности, а также вспомним, что называют коэффициентом полезного действия механизма.

Урок 31. Механическая работа. Мощность (практика)

На этом занятии мы рассмотрим решения задач на расчет механической работы для различных ситуаций (работа силы тяжести, силы упругости и силы трения). Научимся рассчитывать значение средней механической мощности и коэффициента полезного действия механизма.

Урок 32. Кинетическая и потенциальная энергия. ЗСЭ

В этом видеоуроке мы вспомним, что называют механической энергией системы. Повторим понятие «кинетическая энергия». Вспомним и о потенциальной энергии тела при гравитационном взаимодействии и о потенциальной энергии упруго деформированного тела. А также повторим формулировку одного из фундаментальных законов природы — закона сохранения и превращения энергии.

Урок 33. Кинетическая энергия. Теорема о кинетической энергии (практика)

В данном уроке мы рассмотрим решение задач с применением теоремы о кинетической энергии, которая, как известно, справедлива независимо от того, какие силы действуют на тело: сила упругости, сила трения или сила тяжести. Научимся находить долю потерянной энергии при неупругом соударении двух тел.

Урок 34. Потенциальная энергия (практика)

Потенциальная энергия — это энергия системы, определяемая взаимным расположением тел (или частей тела друг относительно друга) и характером сил взаимодействия между ними. На этом занятии мы научимся рассчитывать потенциальную энергию тела, как в гравитационном поле Земли, так и при упругой деформации тела.

Урок 35. Закон сохранения и изменения механической энергии (практика)

Единой количественной мерой движения материи, не зависящей от форм этого движения, является энергия. Знание уравнений, выражающих закон сохранения и превращения энергии, позволяет при известном навыке решать почти все задачи механики на движение тел. В процессе разбора задач на закон сохранения и превращения энергии мы и попытаемся сформировать этот навык.

Урок 36. Гармонические колебания. Характеристики гармонических колебаний

На этом уроке мы с вами вспомним, какое движение называется колебательным и что называют свободными колебаниями. Повторим основные характеристики колебательного движения. Вспомним, какие колебания называются гармоническими и рассмотрим, какие превращения энергии происходят при гармонических колебаниях.

Урок 37. Гармонические колебания и их характеристики (практика)

Наиболее простой вид колебаний — это гармонические колебания. Они подчиняются закону синуса или косинуса. Рассматривая данный вид колебаний, мы пренебрегаем потерями энергии. Именно такие задачи мы и будем решать на данном занятии.

Урок 38. Математический и пружинный маятники

На этом занятии мы с вами вспомним, какой маятник называют математическим, а какой пружинным. Рассмотрим условия возникновения свободных гармонических колебаний в таких системах. А также вспомним формулы, по которым можно рассчитать период свободных колебаний математического и пружинного маятников.

Урок 39. Математический и пружинный маятники (практика)

При решении данного типа задач необходимо вначале определить, чему равно ускорение точки подвеса математического или пружинного маятников и являются ли колебания малыми. При решении задач этой группы следует отчетливо представлять, что период (частота) собственных колебаний определяется только параметрами колебательной системы, а амплитуда и начальная фаза колебаний зависят от того, каким образом систему вывели из состояния равновесия.

Урок 40. Вынужденные колебания. Резонанс

В данном видеоуроке мы с вами вспомним, какие колебания называются вынужденными. Рассмотрим особенности вынужденных колебаний. Поговорим о явлении механического резонанса. А также вспомним об автоколебаниях и автоколебательных системах.

Урок 41. Вынужденные колебания. Резонанс (практика)

На этом занятии мы подробно разберем решения некоторых задач на вынужденные колебания и задач, связанных с явлением механического резонанса.

Урок 42. Механические волны и их основные характеристики

На уроке мы вспомним, что называют «механической волной». Рассмотрим особенности распространения волн. А также повторим виды волн и их основные характеристики. Вспомним о явлениях интерференции и дифракции механических волн.

Урок 43. Механические волны и их основные характеристики (практика)

При решении задач этой группы особое внимание следует обращать на механизм возникновения упругих волн и на процессы переноса энергии. Если тело, которое колеблется, находится в упругой среде, то частицы среды, соприкасающиеся с ним, так же совершают колебательные движения. Благодаря взаимодействию соседних элементов среды упругие деформации передаются от одних ее участников к другим. Таким образом, при распространении колебаний в упругой среде имеет место перенос энергии упругой деформации без переноса массы. Это необходимо учитывать при решении задач.

Урок 44. Звук. Скорость звука

Мы с вами вспомним, что называют «звуком». Рассмотрим условия возникновения и распространения звуковых волн. Вспомним от чего зависит скорость звуковых волн. Повторим некоторые характеристики звука. А также рассмотрим наиболее часто встречающиеся в повседневной жизни звуковые явления.

Урок 45. Звук. Скорость звука (практика)

Звуковыми или акустическими волнами называется процесс распространения в среде колебаний с частотой в пределах 16 — 20000 Гц, воспринимаемых ухом человека как звук. Так как звук — это волна, то ему присуще все те характеристики, что и обычной механической волне. Это следует учитывать при решении задач.

Источник

Описание презентации по отдельным слайдам:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Материал подходит для УМК

Другие материалы

Вам будут интересны эти курсы:

Скачать:

Подписи к слайдам:

Подписи к слайдам:

Подписи к слайдам:

По теме: методические разработки, презентации и конспекты

Открытый урок: «Законы сохранения в механике».

1. Механика

2. Из теории вопроса

3. Первый закон Ньютона

4. Основная модель – материальная точка.

5. ИНСО

6. Второй закон Ньютона

7. Движение и силы

8. Третий закон Ньютона

9. Невесомая нерастяжимая нить

10. Наклонная плоскость

11. Обозначая на схеме силы,

12. Сила- векторная величина.

13. Решение динамических задач

14. Алгоритм решения задач с использованием 2 закона.

15. Алгоритм решения задач

16. Задания части А

17. Часть А

18. Часть А

19. Часть А

20. Часть С

21. Подсказки для решения задачи.

22. Подсказки для решения задачи

Урок 1. Основные понятия кинематики. Относительность движения

Урок 2. Основные понятия кинематики. Относительность движения (практика)

Урок 3. Равномерное прямолинейное движение. Скорость

Урок 4. Равномерное прямолинейное движение. Скорость (практика)

Урок 5. Равноускоренное прямолинейное движение. Ускорение

Урок 6. Равноускоренное прямолинейное движение. Ускорение (практика)

Урок 7. Свободное падение. Ускорение свободного падения

Урок 8. Свободное падение. Ускорение свободного падения (практика)

Урок 9. Движение точки по окружности

Урок 10. Движение точки по окружности (практика)

Урок 11. ИСО. Первый закон Ньютона

Урок 12. Масса и плотность тела

Урок 13. Первый закон Ньютона. Масса и плотность тела (практика)

Урок 14. Сила. Второй и третий законы Ньютона

Урок 15. Сила. Второй и третий законы Ньютона (практика)

Урок 16. Закон всемирного тяготения. Сила тяжести

Урок 17. Закон всемирного тяготения. Сила тяжести (практика)

Урок 18. Сила упругости. Закон Гука

Урок 19. Сила упругости. Закон Гука (практика)

Урок 20. Силы трения. Коэффициент трения

Урок 21. Силы трения. Коэффициент трения (практика)

Урок 22. Момент силы. Условия равновесия твёрдого тела

Урок 23. Момент силы. Условия равновесия твёрдого тела (практика)

Урок 24. Давление твёрдых тел, жидкостей и газов. Закон Паскаля

Урок 25. Давление твёрдых тел, жидкостей и газов. Закон Паскаля (практика)

Урок 26. Закон Архимеда. Условия плавания тел

Урок 27. Закон Архимеда. Условия плавания тел (практика)

Урок 28. Импульс. Закон сохранения импульса

Урок 29. Импульс. Закон сохранения импульса (практика)

Урок 30. Механическая работа. Мощность

Урок 31. Механическая работа. Мощность (практика)

Урок 32. Кинетическая и потенциальная энергия. ЗСЭ

Урок 33. Кинетическая энергия. Теорема о кинетической энергии (практика)

Урок 34. Потенциальная энергия (практика)

Урок 35. Закон сохранения и изменения механической энергии (практика)

Урок 36. Гармонические колебания. Характеристики гармонических колебаний

Урок 37. Гармонические колебания и их характеристики (практика)

Урок 38. Математический и пружинный маятники

Урок 39. Математический и пружинный маятники (практика)

Урок 40. Вынужденные колебания. Резонанс

Урок 41. Вынужденные колебания. Резонанс (практика)

Урок 42. Механические волны и их основные характеристики

Урок 43. Механические волны и их основные характеристики (практика)

Урок 44. Звук. Скорость звука

Урок 45. Звук. Скорость звука (практика)

Новое и интересное на сайте: