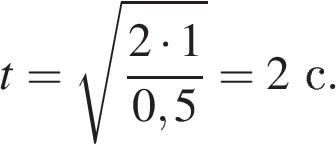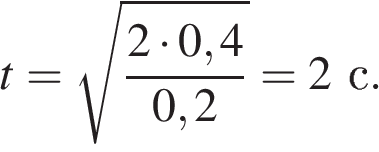Егэ физика 4623 - Помощь в подготовке к экзаменам и поступлению

Тело, брошенное вертикально вверх с поверхности Земли, достигло максимальной высоты 5 м. С какой начальной скоростью тело было брошено вверх? (Ответ дайте в метрах в секунду.) Сопротивлением воздуха пренебречь. Ускорение свободного падения считать равным 10 м/с².

Спрятать решение

Решение.

Поскольку сопротивлением воздух можно пренебречь, для тела выполняется закон сохранения энергии, а значит, вся начальная кинетическая энергия переходит в потенциальную энергию: Отсюда сразу находим начальную скорость:

Ответ: 10.

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток. Вариант 5.

Источник

22.
Задание 4 № 4518.
Тело массой 1 кг, брошенное
вертикально вверх с поверхности
Земли, достигло максимальной
высоты 20 м. Какой кинетической
энергией обладало тело
тотчас после броска? Сопротивлением
воздуха пренебречь.

1)
400 Дж

2)
100 Дж

3)
200 Дж

4)
2 кДж

Решение.

Поскольку
сопротивлением воздуха
можно пренебречь, для тела
выполняется закон сохранения
энергии. А значит, вся имевшаяся
вначале кинетическая
энергия переходит в
потенциальную, когда тело
находится в верхней точке
траектории. Таким образом,
кинетическая энергия тела
тотчас после броска равна

Правильный
ответ указан под номером 3.

Ответ:
3

4518

Источник:
ЕГЭ по физике 06.06.2013. Основная
волна. Дальний Восток. Вариант
2.

23.
Задание 4 № 4553.
Камень массой 1 кг падает на
землю с высоты 30 м из состояния
покоя. Какую кинетическую
энергию имеет камень перед ударом
о землю? Сопротивлением
воздуха пренебречь.

1)
300 Дж

2)
45 Дж

3)
450 Дж

4)
3000 Дж

Решение.

Поскольку
сопротивлением воздуха
можно пренебречь, для камня
выполняется закон сохранения
энергии. А значит, кинетическая
энергия перед ударом о землю равна
изменению потенциальной
энергии, взятому со знаком
минус. Таим образом, искомая
кинетическая энергия
равна

Правильный
ответ: 1

Ответ:
1

4553

Источник:
ЕГЭ по физике 06.06.2013. Основная
волна. Дальний Восток. Вариант
3.

24.
Задание 4 № 4623.
Тело, брошенное вертикально
вверх с поверхности Земли,
достигло максимальной
высоты 5 м. С какой начальной
скоростью тело было брошено
вверх? Сопротивлением
воздуха пренебречь.

1)
40 м/с

2)
10 м/с

3)
5 м/с

4)
20 м/с

Решение.

Поскольку
сопротивлением воздух
можно пренебречь, для тела
выполняется закон сохранения
энергии, а значит, вся начальная
кинетическая энергия
переходит в потенциальную
энергию:
.
Отсюда сразу находим
начальную скорость:

Правильный
ответ: 2

Ответ:
2

4623

Источник:
ЕГЭ по физике 06.06.2013. Основная
волна. Дальний Восток. Вариант
5.

25.
Задание 4 № 4728.
Скорость груза массой 0,2 кг равна
1 м/с. Кинетическая энергия
груза равна

1)
0,1 Дж

2)
0,5 Дж

3)
0,3 Дж

4)
0,2 Дж

Решение.

Кинетическая
энергия груза равна

Правильный
ответ: 1

Ответ:
1

4728

Источник:
ЕГЭ по физике 06.06.2013. Основная
волна. Сибирь. Вариант 1.

26.
Задание 4 № 4763.
Самосвал массой
при
движении на пути к карьеру
имеет кинетическую энергию
2,510
Дж. Какова его кинетическая
энергия после загрузки, если
он двигался с прежней скоростью,
а масса его увеличилась в 2 раза?

1)
10
Дж

2)
2,510
Дж

3)
510
Дж

4)
1,2510
Дж

Решение.

Кинетическая
энергия пропорциональна
массе тела:

Таким
образом, после загрузки при
движении со такой же скоростью
самосвал будет иметь вдвое большую
кинетическую энергию:

Правильный
ответ: 3

Ответ:
3

4763

Источник:
ЕГЭ по физике 06.06.2013. Основная
волна. Сибирь. Вариант 2.

27.
Задание 4 № 4798.
Кинетическая энергия
автомобиля массой 500 кг,
движущегося со скоростью
36 км/ч, равна

1)
324 000 Дж

2)
25 000 Дж

3)
12 500 Дж

4)
5000 Дж

Решение.

Сперва
переведем скорость из км/ч
в м/с:

Кинетическая
энергия автомобиля равна

Правильный
ответ: 2

Ответ:
2

4798

Источник:
ЕГЭ по физике 06.06.2013. Основная
волна. Сибирь. Вариант 3.

28.
Задание 4 № 4833.
Скорость груза массой 0,4 кг равна
2 м/с. Кинетическая энергия
груза равна

1)
0,16 Дж

2)
0,8 Дж

3)
0,32 Дж

4)
0,4 Дж

Решение.

Кинетическая
энергия груза равна

Правильный
ответ: 2

Ответ:
2

4833

Источник:
ЕГЭ по физике 06.06.2013. Основная
волна. Сибирь. Вариант 4.

29.
Задание 4 № 5148.
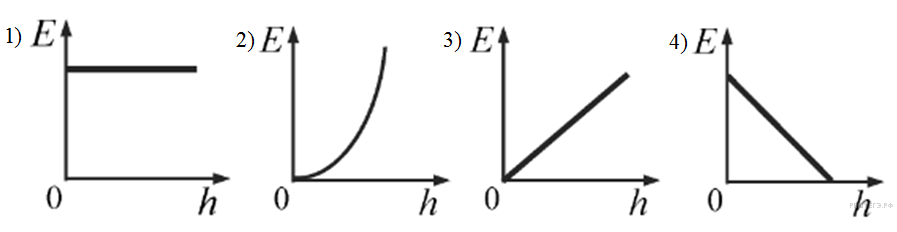
Какой из графиков, приведённых
на рисунке, показывает
зависимость полной энергии
E
тела, брошенного под углом к
горизонту, от его высоты
h
над Землёй? Сопротивлением
воздуха пренебречь.

1)
1

2)
2

3)
3

4)
4

Решение.

Поскольку
сопротивлением воздуха
можно пренебречь, для тела
выполняется закон сохранения
полной механической
энергии. Таким образом,
правильный график представлен
на рисунке 1.

Правильный
ответ: 1

Ответ:
1

5148

Источник:
ЕГЭ по физике 06.06.2013. Основная
волна. Урал. Вариант 2.

30.
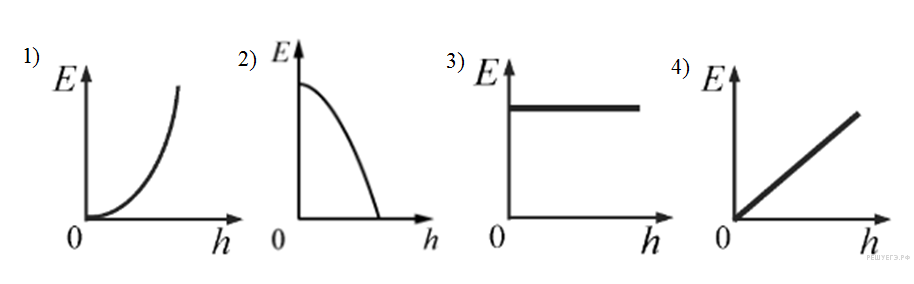
Задание 4 № 5218.
Какой из графиков изображает
зависимость полной
механической энергии E
свободно падающего
тела от его высоты h
над Землёй? Сопротивлением
воздуха пренебречь.

1)
1

2)
2

3)
3

4)
4

Решение.

Правильный
ответ: 3

Ответ:
3

5218

Источник:
ЕГЭ по физике 06.06.2013. Основная
волна. Урал. Вариант 4.

31.
Задание 4 № 5463.
Для
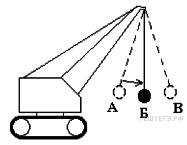
разрушения преграды часто
используют массивный шар,
раскачиваемый на стреле
подъёмного крана (см. рисунок).
Какие преобразования
энергии происходят при
перемещении шара из положения
А в положение Б?

1)
внутренняя энергия шара
преобразуется в его
кинетическую энергию

2)
кинетическая энергия шара
преобразуется в его
потенциальную энергию

3)
потенциальная энергия
шара преобразуется в его
кинетическую энергию

4)
внутренняя энергия шара
преобразуется в его
потенциальную энергию

Решение.

Шар,
раскачиваемый на стреле
подъемного крана представляет
собой математический
маятник. Для математического
маятника выполняется
закон сохранения полной
механической энергии.
Положение А есть положение
максимального отклонения,
в нем кинетическая энергия
обращается в ноль, а
потенциальная энергия
максимальна. Напротив,
положение Б — положение
равновесия. В нем кинетическая
энергия максимальна, а
потенциальная достигает
своего минимума. Таким
образом, при перемещении
шара из положения А в положение
Б потенциальная энергия
шара преобразуется в его
кинетическую энергию.
Внутренняя энергия шара,
связанная с тепловым
движением молекул в шаре
и с их взаимодействием
между собой, при этом не изменяется.

Правильный
ответ указан под номером: 3.

Ответ:
3

5463

Источник:
ЕГЭ по физике 06.06.2013. Основная
волна. Центр. Вариант 4.

32.
Задание 4 № 5498.
Искусственный спутник
обращается вокруг Земли
по вытянутой эллиптической
орбите. Выберите верное
утверждение о значениях
кинетической энергии и
полной механической
энергии спутника.

1)
Кинетическая энергия
достигает минимального
значения в точке минимального
удаления от Земли, полная
механическая энергия
спутника неизменна.

2)
Кинетическая энергия
достигает минимального
значения в точке максимального
удаления от Земли, полная
механическая энергия
спутника неизменна.

3)
Кинетическая и полная
механическая энергия
спутника достигают
минимальных значений в
точке минимального удаления
от Земли.

4)
Кинетическая и полная
механическая энергия
спутника достигают
минимальных значений в
точке максимального удаления
от Земли.

Решение.

Т. к
спутник вращается только
в поле гравитационного
притяжения Земли, то выполняется
закон сохранения энергии, а
значит, полная механическая
энергия спутника неизменна.

Чем
больше кинетическая
энергия, тем меньше потенциальная,
и чем больше потенциальная,
тем меньше кинетическая.

Потенциальная
энергия спутника зависит
от расстояния до центра Земли
следующим образом:

Следовательно,
чем больше расстояние
,
тем больше значение потенциальной
энергии (обратите внимание
на знак ««).
Таким образом, потенциальная
энергия достигает
максимального значения
в точке максимального
удаления от Земли, а кинетическая
энергия — минимума в этой
точке.

Правильный
ответ указан под номером 2.

Ответ:
2

5498

Источник:
ЕГЭ по физике 06.06.2013. Основная
волна. Центр. Вариант 6.

33.
Задание 4 № 6042.
Кинетическая энергия
некоторого тела увеличилась,
а потенциальная — уменьшилась.
Полная механическая
энергия этого тела

1)
обязательно увеличилась

2)
обязательно уменьшилась

3)
осталась неизменной

4)
могла увеличиться, уменьшиться
или остаться неизменной

Решение.

Полная
механическая энергия тела
не изменяется, если на тело
не действуют диссипативные
силы. В условии задачи ничего
не сказано, о наличии или
отсутствии диссипативных
сил, поэтому полная механическая
энергия этого тела могла увеличиться,
уменьшиться или остаться
неизменной.

Правильный
ответ указан под номером: 4.

Ответ:
4

6042

Источник:
МИОО: Диагностическая
работа по физике 10.12.2013
вариант ФИ10201.

34.
Задание 4 № 6077.
Кинетическая энергия
некоторого тела уменьшилась,
а потенциальная — увеличилась.
Полная механическая
энергия этого тела

1)
обязательно увеличилась

2)
обязательно уменьшилась

3)
осталась неизменной

4)
могла увеличиться, уменьшиться
или остаться неизменной

Решение.

Полная
механическая энергия
складывается из потенциальной
и кинетической. Зная только
то, что кинетическая энергия
уменьшилась, а потенциальная
увеличилась, нельзя сказать
как изменилась полная
механическая энергия,
часть механической энергии
могла перейти, например, в
тепловую энергию при соударении.

Правильный
ответ указан под номером: 4.

Ответ:
4

6077

Источник:
МИОО: Диагностическая
работа по физике 10.12.2013
вариант ФИ10202.

35.
Задание 4 № 6147.
Тяжёлый ящик неподвижно стоит
на наклонной плоскости. Два
школьника сделали по этому
поводу следующие
утверждения.

А.
Так
как ящик неподвижен, то
изменение его кинетической
энергии равно нулю и изменение
его потенциальной энергии
равно нулю.

Б.
В
этой системе действует сила
трения, но полная механическая
энергия ящика сохраняется.

Какое
утверждение верно?

1)
только А

2)
только Б

3)
и А, и Б

4)
ни А, ни Б

Решение.

Проанализируем
оба утверждения.

Утверждение
А.
Скорость тела не изменяется,
значит, не изменяется его
кинетическая энергия.
Высота тела относительно
земли также не изменяется,
следовательно, не изменяется
его потенциальная энергия.
Утверждение А
верно.

Утверждение
Б.
Сила трения уравновешивает
силу тяжести, тянущую тело
вниз по наклонной плоскости.
Так как не изменяются
кинетическая и потенциальная
энергии тела, полная механическая
энергия также остаётся постоянной.

Правильный
ответ указан под номером: 3.

Ответ:
3

6147

Источник:
МИОО: Диагностическая
работа по физике 01.04.2014
вариант ФИ10602.

36.
Задание 4 № 6226.
Два груза одинаковой массы
подняли с одинаковой
исходной высоты в верхнюю
точку наклонной плоскости:
один груз — втаскивая наверх
вдоль наклонной плоскости,
а другой — поднимая вертикально.
При этом модуль работы силы
тяжести, действующей на
грузы,

1)
больше при подъёме груза вертикально
вверх

2)
для первого груза зависит
от угла наклона плоскости

3)
больше при подъёме груза вдоль
наклонной плоскости

4)
одинаковый для обоих грузов

Решение.

Правильный
ответ указан под номером: 4.

Ответ:
4

6226

Источник:
ЕГЭ по физике 05.05.2014. Досрочная
волна. Вариант 2.

37.
Задание 4 № 6263.
Лыжник поднимается на
подъёмнике на вершину горы и затем
скатывается по склону
горы вниз. При этом модуль работы
силы тяжести, действующей
на лыжника,

1)
одинаковый на обоих участках
пути

2)
больше при движении на подъёмнике

3)
зависит от угла крутизны
склона

4)
больше при движении по склону
горы

Решение.

Поле
силы тяжести — поле консервативной
силы. Работа, совершаемая
консервативными силами
не зависит от траектории,
по которой двигалось тело,
а зависит только от начального
и конечного положения
тела. В начале и в конце своего
пути лыжник находится на
одной и той же высоте, поэтому
модуль работы силы тяжести
одинаков при подъёме и спуске.

Правильный
ответ указан под номером: 1.

Ответ:
1

6263

Источник:
ЕГЭ по физике 05.05.2014. Досрочная
волна. Вариант 3.

38.
Задание 4 № 6299.
Лыжник поднимается на
подъёмнике на вершину горы, затем
скатывается по склону
горы вниз и вновь подъезжает к
подъёмнику по горизонтальной
лыжне. При этом суммарная работа
силы тяжести, действующей
на лыжника на всей траектории
его движения,

1)
равна работе, которую
совершает сила трения при
движении по горизонтальному
участку

2)
равна работе, которую
совершает сила тяжести
при движении на подъёмнике

3)
равна работе, которую
совершает сила тяжести
при движении по склону горы

4)
равна нулю

Решение.

Поле
силы тяжести — поле консервативной
силы. Работа, совершаемая
консервативными силами
не зависит от траектории,
по которой двигалось тело,
а зависит только от начального
и конечного положения
тела. В начале и в конце своего
пути лыжник находится на
одной и той же высоте, поэтому
суммарная работа силы
тяжести равна нулю.

Правильный
ответ указан под номером: 4.

Ответ:
4

6299

Источник:
ЕГЭ по физике 05.05.2014. Досрочная
волна. Вариант 4.

39.
Задание 4 № 6335.
Небольшое тело массой 200 г
свободно соскальзывает
вниз по гладкой наклонной
плоскости вдоль оси OX.
В таблице приведена
зависимость проекции v_x
скорости этого тела от времени
t.
Какую работу совершит сила
тяжести к моменту, к которому
тело пройдёт путь 1 м?

t, с	0	1	2	3	4
v_x, м/с	0	0,5	1	1,5	2

1)
10 Дж

2)
2 Дж

3)
0,5 Дж

4)
0,1 Дж

Решение.

Из
таблицы видно, что движение
тела равноускоренное,
следовательно, за время
тело
вдоль оси OX
проходит путь, равный
Найдём
ускорение из таблицы, для
этого нужно выбрать произвольный
промежуток времени,
вычесть из конечной скорости
на промежутке начальную
и разделить получившуюся
разность на длительность
промежутка времени
Ускорение
Найдём,
через какое время тело пройдёт путь 1
м:

Трения
нет, поэтому выполняется
закон сохранения механической
энергии. Тело движется вдоль
оси OX,
при его скольжении вниз
потенциальная энергия
превращается в кинетическую.
Работа, совершённая полем
тяжести над телом равна изменению
потенциальной энергии
взятой с противоположным
знаком. получаем:

Правильный
ответ указан под номером: 4.

Ответ:
4

6335

Источник:
МИОО: Тренировочная работа
по физике 06.05.2014 вариант
ФИ10701.

40.
Задание 4 № 6370.
Небольшое тело массой 500 г
свободно соскальзывает
вниз по гладкой наклонной
плоскости вдоль оси OX.
В таблице приведена
зависимость проекции v_x
скорости этого тела от времени
t.
Какую работу совершит сила
тяжести к моменту, к которому
тело пройдёт путь 0,4 м?

t, с	0	1	2	3	4
v_x, м/с	0	0,2	0,4	0,6	0,8

1)
4 Дж

2)
2 Дж

3)
0,5 Дж

4)
40 мДж

Решение.

Из
таблицы видно, что движение
тела равноускоренное,
следовательно, за время
тело
вдоль оси OX
проходит путь, равный
Найдём
ускорение из таблицы, для
этого нужно выбрать произвольный
промежуток времени,
вычесть из конечной скорости
на промежутке начальную
и разделить получившуюся
разность на длительность
промежутка времени
a=frac{v_2-v_1}{t_2-t_1}. Ускорение
Найдём,
через какое время тело пройдёт путь 0,4
м:

Правильный
ответ указан под номером: 4.

Ответ:
4

6370

Источник:
МИОО: Тренировочная работа
по физике 06.05.2014 вариант
ФИ10702.

41.
Задание 4 № 6723.
Тело массой 2 кг, брошенное с
уровня земли вертикально
вверх со скоростью 10 м/с, упало
обратно на землю. Какой
потенциальной энергией
обладало тело относительно
поверхности земли в верхней
точке траектории? Сопротивлением
воздуха пренебречь. Ответ
приведите в джоулях.

Решение.

Запишем
закон сохранения энергии:

Ответ:
100.

Ответ:
100

6723

100

Источник:
СтатГрад: Диагностическая
работа по физике 06.02.2015
Вариант ФИ10401.

42.
Задание 4 № 6917.
Тела 1 и 2 взаимодействуют
только друг с другом. Изменение
кинетической энергии тела
2 за некоторый промежуток
времени равно 10 Дж. Работа,
которую совершили за этот
же промежуток времени
силы взаимодействия тел 1 и
2, равна 30 Дж. Чему равно изменение
кинетической энергии тела
1 за это время?

Решение.

Т.к.
тела 1 и 2 взаимодействуют
только друг с другом, они образуют
замкнутую систему.

Кинетической
энергией системы называют
сумму кинетических энергий
всех тел, входящих в систему.
,
а изменение кинетической
энергии

Изменение
кинетической энергии
системы равно работе всех
внутренних и внешних сил,
действующих на тела системы.
.

Т.о.
получаем

Ответ:
20

6917

Источник:
СтатГрад: Тренировочная
работа по физике 14.04.2015
Вариант ФИ10601

43.
Задание 4 № 6949.
Тела 1 и 2 взаимодействуют
только друг с другом. Изменение
кинетической энергии тела
1 за некоторый промежуток
времени равно 15 Дж. Работа,
которую совершили за этот
же промежуток времени
силы взаимодействия тел 1 и
2, равна 45 Дж. Чему равно изменение
кинетической энергии тела
2 за это время?

Источник

2017-10-29

В железной цилиндрической цистерне высотой 5 м и диаметром 5 м содержится керосин. При температуре $5^{ circ} С$ керосин не доходит до края на 15 см. Рассчитать, при какой температуре керосин начал бы переливаться через край цистерны. Расчет сделать для двух случаев: без учета расширения цистерны и с учетом расширения.

Решение:

1-й случай. Объем керосина в цистерне при $5^{ circ} С$

$V_{1} = hS$,

где

$h = h_{1} — h_{2}, S = frac{ pi d^{2}}{4}$.

После подстановки этих выражений в уравнение получим

$V_{1} = (h_{1} — h_{1}) frac{ pi d^{2}}{4}$,

$V_{1} = frac{4,85 м cdot 3,14 cdot 25 м^{2}}{4} = 95,18 м^{3}$.

Когда керосин при нагревании поднимется до края, его объем будет равен

$V_{2} = h_{1}S = h_{1} frac{ pi d^{2}}{4}$,

$V_{2} = frac{5 м cdot 3,14 cdot 25 м^{2}}{4} = 98,12 м^{3}$.

Объемы $V_{1}$ и $V_{2}$ связаны соотношением

$frac{V_{1}}{V_{2}} = frac{1 + beta t_{1}}{1 + beta t_{2}}$,

откуда

$t_{2} = frac{V_{2} (1 + beta t_{1}) — V_{1}}{V_{1} beta}$.

После подстановки в это равенство значений и вычислений получим

$t_{2} = frac{98,12 м^{2} (1 + 0,001 град^{-1} cdot 5 град) — 95,18 м^{3}} { 95,18 м^{3} cdot 0,001 град^{-1}} approx 36^{ circ} С$.

2-й случай. При $5^{ circ} С$ объем цистерны будет $V_{2}$, а после нагревания до $t_{3}$ ее объем будет $V_{3}$, причем

$frac{V_{2}}{V_{3}} = frac{1 + beta_{1} t_{1}}{1 + beta_{1} t_{3}}$,

где $beta_{1}$ — коэффициент объемного расширения железа. Откуда

$V_{3} = frac{V_{2} ( 1 + beta_{1} t_{3})}{1 + beta_{1} t_{1}}$.

Такой же объем должен занимать керосин при температуре $t_{3}$. Мы уже знаем, что объем керосина при $5^{ circ} С$ равен $V_{1}$, а после нагревания до $t_{3}$ его объем будет $V_{3}$, т. е.

$frac{V_{1}}{V_{3}} = frac{1 + beta t_{1}}{1 + beta t_{3}}$,

Подставив значение $V_{3}$ из предыдущего расчета в полученное соотношение, получим

$frac{V_{1}}{ frac{V_{2} ( 1 + beta_{1} t_{3})}{1 + beta_{1} t_{1}}} = frac{1 + beta t_{1}}{1 + beta t_{3}}$;

$frac{V_{1}( 1 + beta_{1} t_{1})}{ V_{2} (1 + beta_{1} t_{3}) } = frac{1 + beta t_{1}}{1 + beta t_{3}}$;

Откуда

Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H.
а) Докажите, что ∠AHB1 = ∠ACB.
б) Найдите BC, если $$AH=8sqrt{3}$$ и ∠BAC = 60°.

Ответ:

Задание 4623

В остроугольном треугольнике ABC провели высоту BH из точки H на стороны AB и BC опустили перпендикуляры HK и HM соответственно.
а) Докажите, что треугольник MBK подобен треугольнику ABC.
б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH = 2, а радиус окружности, описанной около треугольника ABC равен 4.

Ответ:

Источник

Решу егэ физика 3104

Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!

—>

Задание 7 № 3104

Подвешенный на пружине груз совершает вынужденные гармонические колебания под действием внешней силы, изменяющейся с частотой Установите соответствие между физическими величинами, характеризующего этот процесс, и частотами их изменения.

К каждому элементу первого столбца подберите соответствующий элемент из второго и внесите в строку ответов выбранные цифры под соответствующими буквами.

А) Кинетическая энергия груза

Б) Ускорение груза

Под действием силы, меняющейся с частотой груз на пружине совершает вынужденные гармонические колебания с такой же частотой. Следовательно, закон изменения со временем высоты груза относительно положения устойчивого равновесия имеет вид Таким образом, закон изменения ускорения со временем: Отсюда получаем, что частота изменения ускорения груза также равна (Б — 2).

Скорость изменяется по закону: Отсюда получаем, что кинетическая энергия груза изменяется по закону

Следовательно, частота изменения кинетической энергии равна (А — 3). Наконец, закон изменения потенциальной энергии груза:

Таким образом, период ее изменения равен (В — 2).

Разве частота изменения и потенциальной, и кинетической энергий не 2V?

В случае вертикальных колебаний груза на пружине надо быть очень аккуратным в терминологии. Попробую пояснить, в чем тут дело (при этом, к сожалению, не могу гарантировать, что все создатели задач для ЕГЭ дают себе отчет в данном вопросе, расскажу так, как есть на самом деле).

С кинетической энергия груза все просто, она действительно изменяется с удвоенной частотой, а вот с потенциальной энергией надо быть осторожнее. Потенциальная энергия всегда связана с работой некоторой потенциальной силы. При вертикальных колебаниях в пружинном маятнике есть две такие силы: меняется как потенциальная энергия груза в поле тяжести (), так и потенциальная энергия деформации пружины (). Как отмечено в решении, потенциальная энергия груза изменяется по гармоническому закону с такой же частотой, с которой происходят колебания, так как она определяется только высотой тела над поверхностью Земли. А вот энергия пружины вообще изменяется не по гармоническому закону.

Почему так? Ответ очень прост. У вертикального пружинного маятника положение равновесия соответствует растянутой пружине: когда мы подвешиваем груз, он сразу растягивает пружину на некоторую величину, которую можно найти из второго закона Ньютона для тела: . При этом, если мы будем искать энергию пружины, то обязаны учитывать это начальное растяжение. В результате, при колебаниях потенциальная энергия пружины изменяется по закону:

Легко видеть, что в законе изменения энергии пружины со временем есть и, и, то есть частота колебаний получается тоже.

—>

Задание 7 № 3104

Попробую пояснить, в чем тут дело при этом, к сожалению, не могу гарантировать, что все создатели задач для ЕГЭ дают себе отчет в данном вопросе, расскажу так, как есть на самом деле.

Phys-ege. sdamgia. ru

26.07.2019 2:00:34

2019-07-26 02:00:34

Источники:

Http://phys-ege. sdamgia. ru/problem? id=3104

Гущин решу егэ физика. Подготовка к ЕГЭ по физике: примеры, решения, объяснения » /> » /> .keyword { color: red; } Решу егэ физика 3104

Гущин решу егэ физика. Подготовка к ЕГЭ по физике: примеры, решения, объяснения

2) СТРУКТУРА КИМов — 2018 и 2019 по сравнению с 2017г. несколько ИЗМЕНИЛАСЬ: Вариант экзаменационной работы будет состоять из двух частей и включит в себя 32 задания. Часть 1 будет содержать 24 задания с кратким ответом, в том числе задания с самостоятельной записью ответа в виде числа, двух чисел или слова, а также задания на установление соответствия и множественный выбор, в которых ответы необходимо записать в виде последовательности цифр. Часть 2 будет содержать 8 заданий, объединенных общим видом деятельности – решение задач. Из них 3 задания с кратким ответом (25–27) и 5 заданий (28–32), для которых необходимо привести развернутый ответ. В работу будут включены задания трех уровней сложности. Задания базового уровня включены в часть 1 работы (18 заданий, из которых 13 заданий с записью ответа в виде числа, двух чисел или слова и 5 заданий на соответствие и множественный выбор). Задания повышенного уровня распределены между частями 1 и 2 экзаменационной работы: 5 заданий с кратким ответом в части 1, 3 задания с кратким ответом и 1 задание с развернутым ответом в части 2. Последние четыре задачи части 2 являются заданиями высокого уровня сложности. Часть 1 экзаменационной работы будет включать два блока заданий: первый проверяет освоение понятийного аппарата школьного курса физики, а второй – овладение методологическими умениями. Первый блок включает 21 задание, которые группируются, исходя из тематической принадлежности: 7 заданий по механике, 5 заданий по МКТ и термодинамике, 6 заданий по электродинамике и 3 по квантовой физике.

Новым заданием базового уровня сложности является последнее задание первой части (24 позиция), приуроченное к возвращению курса астрономии в школьную программу. Задание имеет характеристику типа «выбор 2 суждений из 5». Задание 24, как и другие аналогичные задания в экзаменационной работе, оценивается максимально в 2 балла, если верно указаны оба элемента ответа, и в 1 балл, если в одном из элементов допущена ошибка. Порядок записи цифр в ответе значения не имеет. Как правило, задания будут иметь контекстный характер, т. е. часть данных, необходимых для выполнения задания будут приводиться в виде таблицы, схемы или графика.

В соответствии с этим заданием в кодификаторе добавился подраздел «Элементы астрофизики» раздела «Квантовая физика и элементы астрофизики», включающий следующие пункты:

· Солнечная система: планеты земной группы и планеты-гиганты, малые тела Солнечной системы.

· Звёзды: разнообразие звездных характеристик и их закономерности. Источники энергии звезд.

· Современные представления о происхождении и эволюции Солнца и звёзд. Наша галактика. Другие галактики. Пространственные масштабы наблюдаемой Вселенной.

· Современные взгляды на строение и эволюцию Вселенной.

Подробнее о структуре КИМ-2018 Вы можете узнать, посмотрев вебинар с участием М. Ю. Демидовой https://www. youtube. com/watch? v=JXeB6OzLokU либо в документе, приведенном ниже.

Подготовка к ОГЭ и ЕГЭ

Среднее общее образование

Линия УМК А. В. Грачева. Физика (10-11) (баз., углубл.)

Линия УМК А. В. Грачева. Физика (7-9)

Линия УМК А. В. Перышкина. Физика (7-9)

Подготовка к ЕГЭ по физике: примеры, решения, объяснения

Лебедева Алевтина Сергеевна, учитель физики, стаж работы 27 лет. Почетная грамота Министерства образования Московской области (2013 год), Благодарность Главы Воскресенского муниципального района (2015 год), Грамота Президента Ассоциации учителей математики и физики Московской области (2015 год).

В работе представлены задания разных уровней сложности: базового, повышенного и высокого. Задания базового уровня, это простые задания, проверяющие усвоение наиболее важных физических понятий, моделей, явлений и законов. Задания повышенного уровня направлены на проверку умения использовать понятия и законы физики для анализа различных процессов и явлений, а также умения решать задачи на применение одного-двух законов (формул) по какой-либо из тем школьного курса физики. В работе 4 задания части 2 являются заданиями высокого уровня сложности и проверяют умение использовать законы и теории физики в измененной или новой ситуации. Выполнение таких заданий требует применения знаний сразу из двух трех разделов физики, т. е. высокого уровня подготовки. Данный вариант полностью соответствует демонстрационному варианту ЕГЭ 2017 года, задания взяты из открытого банка заданий ЕГЭ.

На рисунке представлен график зависимости модуля скорости от времени T . Определите по графику путь, пройденный автомобилем в интервале времени от 0 до 30 с.

Решение. Путь, пройденный автомобилем в интервале времени от 0 до 30 с проще всего определить как площадь трапеции, основаниями которой являются интервалы времени (30 – 0) = 30 c и (30 – 10) = 20 с, а высотой является скорость V = 10 м/с, т. е.

S =	(30 + 20) С	10 м/с = 250 м.
2

Ответ. 250 м.

Груз массой 100 кг поднимают вертикально вверх с помощью троса. На рисунке приведена зависимость проекции скорости V груза на ось, направленную вверх, от времени T . Определите модуль силы натяжения троса в течение подъема.

Решение. По графику зависимости проекции скорости V груза на ось, направленную вертикально вверх, от времени T , можно определить проекцию ускорения груза

A =	∆V	=	(8 – 2) м/с	= 2 м/с 2 .
∆T	3 с

На груз действуют: сила тяжести, направленная вертикально вниз и сила натяжения троса, направленная вдоль троса вертикально вверх смотри рис. 2. Запишем основное уравнение динамики. Воспользуемся вторым законом Ньютона. Геометрическая сумма сил действующих на тело равна произведению массы тела на сообщаемое ему ускорение.

Запишем уравнение для проекции векторов в системе отсчета, связанной с землей, ось OY направим вверх. Проекция силы натяжения положительная, так как направление силы совпадает с направлением оси OY, проекция силы тяжести отрицательная, так как вектор силы противоположно направлен оси OY, проекция вектора ускорения тоже положительная, так тело движется с ускорением вверх. Имеем

T – Mg = Ma (2);

Из формулы (2) модуль силы натяжения

Т = M (G + A ) = 100 кг (10 + 2) м/с 2 = 1200 Н.

Ответ . 1200 Н.

Тело тащат по шероховатой горизонтальной поверхности с постоянной скоростью модуль которой равен 1, 5 м/с, прикладывая к нему силу так, как показано на рисунке (1). При этом модуль действующей на тело силы трения скольжения равен 16 Н. Чему равна мощность, развиваемая силой F ?

Решение. Представим себе физический процесс, заданный в условии задачи и сделаем схематический чертеж с указанием всех сил, действующих на тело (рис.2). Запишем основное уравнение динамики.

Выбрав систему отсчета, связанную с неподвижной поверхностью, запишем уравнения для проекции векторов на выбранные координатные оси. По условию задачи тело движется равномерно, так как его скорость постоянна и равна 1,5 м/с. Это значит, ускорение тела равно нулю. По горизонтали на тело действуют две силы: сила трения скольжения тр. и сила, с которой тело тащат. Проекция силы трения отрицательная, так как вектор силы не совпадает с направлением оси Х . Проекция силы F положительная. Напоминаем, для нахождения проекции опускаем перпендикуляр из начала и конца вектора на выбранную ось. С учетом этого имеем: F cosα – F тр = 0; (1) выразим проекцию силы F , это F cosα = F тр = 16 Н; (2) тогда мощность, развиваемая силой, будет равна N = F cosα V (3) Сделаем замену, учитывая уравнение (2), и подставим соответствующие данные в уравнение (3):

N = 16 Н · 1,5 м/с = 24 Вт.

Ответ. 24 Вт.

Груз, закрепленный на легкой пружине жесткостью 200 Н/м, совершает вертикальные колебания. На рисунке представлен график зависимости смещения X груза от времени T . Определите, чему равна масса груза. Ответ округлите до целого числа.

Решение. Груз на пружине совершает вертикальные колебания. По графику зависимости смещения груза Х от времени T , определим период колебаний груза. Период колебаний равен Т = 4 с; из формулы Т = 2π выразим массу M груза.

=	T	;	M	=	T 2	; M = K	T 2	; M = 200 H/м	(4 с) 2	= 81,14 кг ≈ 81 кг.
2π	K	4π 2	4π 2	39,438

Ответ: 81 кг.

На рисунке показана система из двух легких блоков и невесомого троса, с помощью которого можно удерживать в равновесии или поднимать груз массой 10 кг. Трение пренебрежимо мало. На основании анализа приведенного рисунка выберите Два верных утверждения и укажите в ответе их номера.

Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 100 Н. Изображенная на рисунке система блоков не дает выигрыша в силе. H , нужно вытянуть участок веревки длиной 3H . Для того чтобы медленно поднять груз на высоту HH .

Решение. В данной задаче необходимо вспомнить простые механизмы, а именно блоки: подвижный и неподвижный блок. Подвижный блок дает выигрыш в силе в два раза, при этом участок веревки нужно вытянуть в два раза длиннее, а неподвижный блок используют для перенаправления силы. В работе простые механизмы выигрыша не дают. После анализа задачи сразу выбираем нужные утверждения:

Для того чтобы медленно поднять груз на высоту H , нужно вытянуть участок веревки длиной 2H . Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 50 Н.

В сосуд с водой полностью погружен алюминиевый груз, закрепленный на невесомой и нерастяжимой нити. Груз не касается стенок и дна сосуда. Затем в такой же сосуд с водой погружают железный груз, масса которого равна массе алюминиевого груза. Как в результате этого изменятся модуль силы натяжения нити и модуль действующей на груз силы тяжести?

Увеличивается; Уменьшается; Не изменяется.

Решение. Анализируем условие задачи и выделяем те параметры, которые не меняются в ходе исследования: это масса тела и жидкость, в которую погружают тело на нити. После этого лучше выполнить схематический рисунок и указать действующие на груз силы: сила натяжения нити F упр, направленная вдоль нити вверх; сила тяжести, направленная вертикально вниз; архимедова сила A , действующая со стороны жидкости на погруженное тело и направленная вверх. По условию задачи масса грузов одинакова, следовательно, модуль действующей на груз силы тяжести не меняется. Так как плотность грузов разная, то объем тоже будет разный

Плотность железа 7800 кг/м 3 , а алюминиевого груза 2700 кг/м 3 . Следовательно, V ж

Подробнее о структуре КИМ-2018 Вы можете узнать, посмотрев вебинар с участием М.

Testet. ru

29.07.2018 9:26:26

2018-07-29 09:26:26

Источники:

Http://testet. ru/biogafii/gushchin-reshu-ege-fizika-podgotovka-k-ege-po-fizike-primery. html

Решу егэ по физике онлайн. Материалы для подготовки к егэ по физике » /> » /> .keyword { color: red; } Решу егэ физика 3104

Решу егэ по физике онлайн. Материалы для подготовки к егэ по физике

ЕГЭ по физике – экзамен, который не входит в перечень испытаний обязательных для сдачи всеми выпускниками. Физику выбирают потенциальные студенты инженерных специальностей. Причем, каждый ВУЗ устанавливает свою планку – в престижных учебных заведениях она может быть очень высокой. Это должен понимать выпускник, начиная подготовку к экзамену. Цель экзамена – проверка уровня знаний и умений, полученных в ходе школьного обучения, на соответствие нормам и стандартам, указанным в программе.

На экзамен отводится практически 4 часа – 235 минут, это время необходимо правильно распределить между заданиями, чтобы успешно справиться со всеми, не теряя ни одной минуты. Разрешается брать с собой калькулятор, поскольку для выполнения заданий требуется множество сложных расчетов. Также можно взять линейку. Работа состоит из трех частей, каждая имеет свои особенности, состоит из заданий разного уровня сложности.

Физика относится к сложным предметам, приблизительно каждый 15-1 сдает этот экзамен ежегодно, чтобы поступить в технический ВУЗ. Предполагается, что выпускник с такими целями не будет учить предмет «с нуля», чтобы подготовиться к ЕГЭ.
Чтобы удачно пройти испытание, необходимо:

Начинать повторение материала заранее, подходить к вопросу комплексно; Активно применять теорию на практике – решать много заданий разного уровня сложности; Заниматься самообразованием; Проходить онлайн тестирование по вопросам за прошлые годы.

Подготовка к ОГЭ и ЕГЭ

Среднее общее образование

Линия УМК А. В. Грачева. Физика (10-11) (баз., углубл.)

Линия УМК А. В. Грачева. Физика (7-9)

Линия УМК А. В. Перышкина. Физика (7-9)

Подготовка к ЕГЭ по физике: примеры, решения, объяснения

S =	(30 + 20) С	10 м/с = 250 м.
2

Ответ. 250 м.

A =	∆V	=	(8 – 2) м/с	= 2 м/с 2 .
∆T	3 с

T – Mg = Ma (2);

Из формулы (2) модуль силы натяжения

Т = M (G + A ) = 100 кг (10 + 2) м/с 2 = 1200 Н.

Ответ . 1200 Н.

N = 16 Н · 1,5 м/с = 24 Вт.

Ответ. 24 Вт.

=	T	;	M	=	T 2	; M = K	T 2	; M = 200 H/м	(4 с) 2	= 81,14 кг ≈ 81 кг.
2π	K	4π 2	4π 2	39,438

Ответ: 81 кг.

Увеличивается; Уменьшается; Не изменяется.

Плотность железа 7800 кг/м 3 , а алюминиевого груза 2700 кг/м 3 . Следовательно, V ж ЕДИНЫЙ ГОСУДАРСТВЕННЫЙ ЭКЗАМЕН ПО ФИЗИКЕ ДЛИТСЯ 235 мин

· Солнечная система: планеты земной группы и планеты-гиганты, малые тела Солнечной системы.

· Звёзды: разнообразие звездных характеристик и их закономерности. Источники энергии звезд.

· Современные взгляды на строение и эволюцию Вселенной.

Подготовка к ОГЭ и ЕГЭ

Среднее общее образование

Линия УМК А. В. Грачева. Физика (10-11) (баз., углубл.)

Линия УМК А. В. Грачева. Физика (7-9)

Линия УМК А. В. Перышкина. Физика (7-9)

Подготовка к ЕГЭ по физике: примеры, решения, объяснения

S =	(30 + 20) С	10 м/с = 250 м.
2

Ответ. 250 м.

A =	∆V	=	(8 – 2) м/с	= 2 м/с 2 .
∆T	3 с

T – Mg = Ma (2);

Из формулы (2) модуль силы натяжения

Т = M (G + A ) = 100 кг (10 + 2) м/с 2 = 1200 Н.

Ответ . 1200 Н.

N = 16 Н · 1,5 м/с = 24 Вт.

Ответ. 24 Вт.

=	T	;	M	=	T 2	; M = K	T 2	; M = 200 H/м	(4 с) 2	= 81,14 кг ≈ 81 кг.
2π	K	4π 2	4π 2	39,438

Ответ: 81 кг.

Увеличивается; Уменьшается; Не изменяется.

Заготовьте этот чудесный, овощной салат, и у вас зимой всегда будет наготове вкусный перекус. У приятный, кисло-сладкий привкус и летний аромат. Овощи тушатся в томатном соусе, поэтому в салате образуется вкусная подливка, которая идеально смягчит гарнир

Описание сделанный своими руками уже долгое количество времени считается не просто вкусным и полезным, а еще и целебным! Не зря в Китае грушевые деревья считаются символом долголетия. Срок их существования намного больше, чем у остальных деревьев. А грек

Здравствуйте, мои дорогие Умные Хозяйки и Хозяева! Признавайтесь, кому уже надоело есть просто так пасхальные яйца😀😀😀?! Для вас рецепт простой и вкусной закуски, которую можно приготовить буквально за пять минут👏! Получается ярко, интересно, красиво! Не с

Внимательно прочитайте текст задания и выберите верный ответ из списка

Решение
→

Задание 18473

Внимательно прочитайте текст задания и выберите верный ответ из списка

Решение
→

Источник

С одноатомным идеальном газом проводят циклический процесс, показанный на рисунке. За цикл газ совершает работу Aц = 5 кДж. Какое количество теплоты газ получает за цикл от нагревателя? Количество вещества газа в ходе процесса остаётся неизменным.

Одноатомный идеальный газ в количестве 10 моль сначала охладили, уменьшив давление в 3 раза, а затем нагрели до первоначальной температуры 300 К (см. рисунок). Какое количество теплоты получил газ на участке 2–3?

Задача 17

Давление насыщенного водяного пара при температуре 40 °С приблизительно равно 6 кПа. Каково парциальное давление водяного пара
в комнате при этой температуре при относительной влажности 30%?

Дано

Pн=6 кПа ф=30% P- ?

Ф=P*100%/Pн

P=Pн*30%/100%=6*0,3=1,8 кПа

Ответ P=1,8кПа

Задача 18

Для определения удельной теплоты плавления в сосуд с водой массой 300 г и температурой 20°С стали бросать кусочки тающего льда при непрерывном помешивании. К моменту времени, когда

лед перестал таять, масса воды увеличилась на 84 г. Определите по данным опыта удельную теплоту плавления льда. Ответ выразите в кДж/кг.

Уравнения количества теплоты Q(воды)=c(воды)*m(воды)*на дельта t и Q(льда)=лямбда(удельная теплота плав. льда)*m(льда). Приравниваем их получаем 4200*0.3*20=Лямбда*0.084, выражаешь лямбда=4200*0.3*20/0.084=300000=300кДж

Задача 19

В одном сосуде находится аргон, а в другом — неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?

Температура — это мера средней кинетической энергии молекул идеального газа а значит, оба газа находятся при одинаковой температуре. Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) термодинамической системы с микроскопическими (масса молекул, средняя скорость их движения) где — концентрация молекул газа.

Тогда отношение концентрации молекул аргона к концентрации молекул неона принимает значение:

Задача 20

В горизонтально расположенной трубке постоянного сечения, запаянной с одного конца, помещен столбик ртути длиной d = 15 см, который отделяет воздух в трубке от атмосферы. Трубку расположили вертикально запаянным концом вниз и нагрели на = 60 К. При этом объем, занимаемый воздухом, не изменился. Атмосферное давление = 750 мм рт.ст. Определите температуру воздуха в лаборатории.

Условие равновесия столбика ртути определяет давление воздуха в вертикальной трубке: , где — атмосферное давление. Здесь Н = 750 мм, — плотность ртути.

Поскольку нагрев воздуха в трубке происходит до температуры и объем, занимаемый воздухом, не изменился, то, согласно уравнению Клапейрона-Менделеева:

Окончательно получаем:К.

Задача 21

В запаянной с одного конца длинной горизонтальной стеклянной трубке постоянного сечения (см. рисунок) находится столбик воздуха длиной l1 = 30,7 см, запертый столбиком ртути. Если трубку поставить вертикально отверстием вверх, то длина воздушного столбика под ртутью будет равна l2 = 23,8 см. Какова длина ртутного столбика? Атмосферное давление 747 мм рт. ст. Температуру воздуха в трубке считать постоянной.

1. Когда трубка расположена горизонтально, объём воздуха и его давление равны, соответственно: , где S — площадь сечения трубки; , что вытекает из условия равновесия столбика ртути.

2. Когда трубка расположена вертикально отверстием вверх, объём закрытой части трубки и давление воздуха в ней равны, соответственно:

где ρ — плотность ртути.

3. Так как T = const, получаем: . , откуда (с учетом того, что 750 мм рт. ст. = 100 000 Па):

Задача 22

В горизонтальном цилиндре с гладкими стенками под массивным поршнем с площадью S находится одноатомный идеальный газ. Поршень соединён с основанием цилиндра пружиной. В начальном состоянии расстояние между поршнем и основанием цилиндра равно L, а давление газа в цилиндре равно внешнему атмосферному давлению p0 (см. рисунок).

Затем газу было передано количество теплоты Q, и в результате поршень медленно переместился вправо на расстояние b. Чему равна жёсткость пружины k?

Тепло, переданное газу, идёт на изменение его внутренней энергии и на совершением им работы:

В начальном состоянии давление и объём газа равны и в конечном состоянии — и Используя уравнение Менделеева — Клапейрона для изменения внутренней энергии получаем:

Чтобы рассчитать работу, заметим, что в каждый момент времени, когда поршень сдвинут на от начального положения давление равно т. е. давление линейно зависит от объёма. Значит, на pV-диаграмме процесс расширения будет изображён отрезком прямой, а фигура под графиком будет являться трапецией, площадь которой равна

Заметим, что этот результат можно получить, посчитав работу газа как минус сумму работ пружины и внешней атмосферы

В итоге

Источник

Задание 4609

Задание 4610

Задание 4611

Задание 4612

Задание 4613

Задание 4614

Задание 4615

Задание 4616

Задание 4617

Задание 4618

Задание 4619

Задание 4620

Задание 4621

Задание 4622

Задание 4623

Источники:

Гущин решу егэ физика. Подготовка к ЕГЭ по физике: примеры, решения, объяснения

Гущин решу егэ физика. Подготовка к ЕГЭ по физике: примеры, решения, объяснения

Подготовка к ЕГЭ по физике: примеры, решения, объяснения

Источники:

Решу егэ по физике онлайн. Материалы для подготовки к егэ по физике

Решу егэ по физике онлайн. Материалы для подготовки к егэ по физике

Подготовка к ЕГЭ по физике: примеры, решения, объяснения

Подготовка к ЕГЭ по физике: примеры, решения, объяснения

Источники:

Задание 18045

Задание 18103

Задание 18111

Задание 18142

Задание 18243

Задание 18615

Задание 18684

Задание 18789

Задание 18478

Задание 18533

Задание 18190

Задание 18785

Задание 17495

Задание 18143

Задание 18207

Задание 18176

Задание 18473

Новое и интересное на сайте: