Поршень может свободно без трения перемещаться вдоль стенок горизонтального цилиндрического сосуда. В объёме, ограниченном дном сосуда и поршнем, находится воздух (см. рис.). Площадь поперечного сечения сосуда равна 20 см2, расстояние от дна сосуда до поршня равно 25 см, атмосферное давление 100 кПа, давление воздуха в сосуде равно атмосферному. Поршень медленно перемещают на 5 см влево, при этом температура воздуха не меняется. Какую силу требуется приложить, чтобы удержать поршень в таком положении? Ответ приведите в ньютонах.
Спрятать решение
Решение.
Воздух в сосуде можно считать идеальным газом. Процесс сжатия газа идет изотермически, а значит, согласно закону Бойля — Мариотта, Отсюда находим давление газа под поршнем в новом положении:
Определим теперь силу, которую необходимо приложить к поршню. Для этого рассмотрим второй закон Ньютона для поршня в проекции на горизонтальную ось: Таким образом, необходимо приложить силу
Ответ: 50.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
|
Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом; II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); III) представлены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); IV) представлен правильный ответ с указанием единиц измерения искомой величины |
2 |
|
Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены преобразования, направленные на решение задачи, но имеется один или несколько из следующих недостатков. Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. И (ИЛИ) В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты. И (ИЛИ) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. И (ИЛИ) Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения величины) |
1 |
|
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1 или 2 балла |
0 |
| Максимальный балл | 2 |
| » Меню сайта |
|
| » Категории раздела | ||||
|
| » Подготовка к ЕГЭ |
 |
| » Кнопка сайта |
 |
| » Код кнопки сайта |
| Решение задач ЕГЭ части С | ||
 |
| » Вход на сайт |
 |
| » Статистика сайта |
|
|
| » Поиск | ||
|
|
| » Погода |
|
Новосибирск — погода |
| » Календарь | |||||||||||||||||||||||||||||||||||||||||
|
2017-10-21
Объем влажного воздуха, находящегося под поршнем в цилиндре при температуре $T_{1}$, изотермически уменьшают до такой величины $V_{1}$, что на стенках цилиндра появляется роса. Затем содержимое цилиндра медленно нагревают до температуры $T_{2}$, одновременно изменяя его объем до величины $V_{2}$. Найти относительную влажность воздуха в конечном состоянии, если давления насыщенных паров при начальной и конечной температурах равны $p_{н1}$ и $p_{н2}$, соответственно.
Решение:
Вспоминая определение точки росы, можно утверждать, что когда объем влажного воздуха уменьшили до величины $V_{1}$, содержащийся в цилиндре пар стал насыщенным. Считая, что к парам вплоть до точки насыщения применимо уравнение Клапейрона—Менделеева, можно утверждать, что количество молей пара, находившегося в цилиндре под поршнем, равно $nu = p_{н1}V_{1} /RT_{1}$, где $R$ — универсальная газовая постоянная. Если предположить, что в конечном состоянии парциальное давление паров меньше $p_{н2}$, то с учетом сделанного выше предположения это давление должно быть равно $p_{2} = nu RT_{2}/V_{2}$. Поскольку согласно определению, используемому в метеорологии, относительная влажность равна отношению парциального давления паров к давлению насыщенных паров данного вещества при той же температуре, искомая относительная влажность должна быть равна
$r = begin{cases} frac{p_{н1}V_{1}T_{2}}{p_{н2}V_{2}T_{1}} cdot 100, & text{при} p_{2} = frac{p_{н1}V_{1}T_{2}}{V_{2}T_{1}} leq p_{н2} \ 100, & text{при} p_{2} geq p_{н2} end{cases}$
Задание 18045
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18103
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18111
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18142
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18243
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18615
Установление соответствия
Решение
→
Задание 18684
Установление соответствия
Решение
→
Задание 18789
Установление соответствия
Решение
→
Задание 18478
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18533
Введите ответ в поле ввода
Решение
→
Задание 18190
Установление соответствия
Решение
→
Задание 18785
Установление соответствия
Решение
→
Задание 17495
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18143
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18207
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18176
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18473
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Подборка тренировочных вариантов ЕГЭ 2023 по физике для 11 класса с ответами из различных источников.
Соответствуют демоверсии ЕГЭ 2023 по физике
→ варианты прошлого года
Тренировочные варианты ЕГЭ 2023 по физике
| ЕГЭ 100 баллов (с ответами) | ||
| Вариант 1 | скачать | |
| Вариант 2 | скачать | |
| Вариант 3 | скачать | |
| Вариант 4 | скачать | |
| Вариант 5 | скачать | |
| Вариант 6 | скачать | |
| vk.com/shkolkovo_fiz | ||
| Вариант 1 | ответы | |
| Вариант 2 | разбор | |
| Вариант 3 | ответы | |
| easy-physic.ru | ||
| Вариант 110 | ответы | разбор |
| Вариант 111 | ответы | разбор |
| Вариант 112 | ответы | разбор |
| Вариант 113 | ответы | разбор |
| Вариант 114 | ответы | разбор |
| Вариант 115 | ответы | разбор |
| Вариант 116 | ответы | разбор |
Примеры заданий:
1. Цилиндрический сосуд разделён лёгким подвижным теплоизолирующим поршнем на две части. В одной части сосуда находится аргон, в другой – неон. Концентрация молекул газов одинакова. Определите отношение средней кинетической энергии теплового движения молекул аргона к средней кинетической энергии теплового движения молекул неона, когда поршень находится в равновесии.
2. Газ получил количество теплоты, равное 300 Дж, при этом внутренняя энергия газа уменьшилась на 100 Дж. Масса газа не менялась. Какую работу совершил газ в этом процессе?
3. Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.
1) При увеличении длины нити математического маятника период его колебаний уменьшается.
2) Явление диффузии протекает в твёрдых телах значительно медленнее, чем в жидкостях.
3) Сила Лоренца отклоняет положительно и отрицательно заряженные частицы, влетающие под углом к линиям индукции однородного магнитного поля, в противоположные стороны.
4) Дифракция рентгеновских лучей невозможна.
5) В процессе фотоэффекта с поверхности вещества под действием падающего света вылетают электроны.
4. В запаянной с одного конца трубке находится влажный воздух, отделённый от атмосферы столбиком ртути длиной l = 76 мм. Когда трубка лежит горизонтально, относительная влажность воздуха ϕ1 в ней равна 80%. Какой станет относительная влажность этого воздуха ϕ2 , если трубку поставить вертикально, открытым концом вниз? Атмосферное давление равно 760 мм рт. ст. Температуру считать постоянно
5. Предмет расположен на главной оптической оси тонкой собирающей линзы. Оптическая сила линзы D = 5 дптр. Изображение предмета действительное, увеличение (отношение высоты изображения предмета к высоте самого предмета) k = 2. Найдите расстояние между предметом и его изображением.
Связанные страницы:
Варианты, ответы и решения ФИ2210401, ФИ2210402, ФИ2210403, ФИ2210404 тренировочная работа №4 статград пробник ЕГЭ 2023 по физике 11 класс в формате реального экзамена ЕГЭ 2023 года, которая прошла 7 марта 2023 года.
Скачать тренировочные варианты
Скачать ответы для вариантов
ФИ2210401_ФИ2210402_ФИ2210403_ФИ2210404
Вариант ФИ2210401 с ответами
1. Два маленьких тела, находившиеся в состоянии покоя, одновременно начинают двигаться из одной точки по плоскости YOX с разными по модулю постоянными ускорениями. На рисунке изображены векторы 1 a и 2 a ускорений этих тел (масштабы координатной сетки вдоль горизонтальной и вертикальной осей одинаковы). Чему равно отношение путей S1/S2, пройденных этими телами за первые 2 секунды их движения?
2. Ускорение свободного падения на поверхности Юпитера в 2,6 раза больше, чем на поверхности Земли. Первая космическая скорость для Юпитера в 5,4 раза больше, чем для Земли. Во сколько раз радиус Юпитера больше радиуса Земли? Ответ округлите до целого числа.
3. На горизонтальном столе лежит лист бумаги, на котором нарисован равнобедренный треугольник с длиной боковой стороны 12 см и углом 30° при основании. В его вершинах расположены одинаковые маленькие тяжёлые бусинки. На каком расстоянии от основания данного треугольника расположен центр тяжести системы, состоящей из этих трёх бусинок?
4. Небольшая шайба массой 50 г соскальзывает с наклонной плоскости с углом при основании 30°. Сопротивление воздуха пренебрежимо мало. В таблице приведены значения модуля скорости V шайбы в различные моменты времени t. Выберите все верные утверждения о результатах этого опыта на основании данных, содержащихся в таблице.
1) Сухое трение между шайбой и плоскостью отсутствует.
2) Модуль ускорения шайбы приблизительно равен 3 м/с2 .
3) За первую секунду движения шайба прошла путь менее 1 м.
4) В момент времени t = 0,4 с модуль импульса шайбы примерно равен 0,06 кг⋅м/с.
5) Если в момент времени t = 1,4 с шайба столкнётся с абсолютно неупругим препятствием, то выделится количество теплоты ≈ 0,44 Дж.
5. На двух узких опорах покоится тяжёлая горизонтальная однородная доска. На доске посередине между опорами лежит гиря. Гирю перекладывают так, что она оказывается лежащей на доске ближе к правой опоре. Как после перекладывания гири изменяются модуль силы реакции правой опоры и момент силы тяжести гири относительно левой опоры? Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
6. На горизонтальном столе установлена в вертикальном положении лёгкая пружина жёсткостью k. Её нижний конец прикреплён к столу, а к верхнему концу прикреплена горизонтальная платформа массой M. На высоте H над платформой удерживают маленький пластилиновый шарик массой m. Шарик отпускают без начальной скорости, после чего он свободно падает и прилипает к покоившейся платформе. В результате этого платформа с шариком начинают совершать колебания, в ходе которых ось пружины остаётся вертикальной, а платформа не касается стола. Установите соответствие между физическими величинами и формулами, выражающими их в рассматриваемой задаче (g – ускорение свободного падения). К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
7. В сосуде объёмом 8,31 л находится 0,35 моль идеального газа при давлении 100 кПа. Газ сначала изотермически расширяют в 2 раза, а затем изохорически нагревают на 120 К. Чему равно давление газа в конечном состоянии? Ответ выразите в кПа и округлите до целого числа.
8. На рисунке приведена зависимость температуры T однородного твёрдого тела массой 2 кг от времени t в процессе нагревания. Чему равна удельная теплоёмкость вещества этого тела? Подводимую к телу тепловую мощность можно считать постоянной и равной 450 Вт.
9. На Т–р-диаграмме показан процесс изменения состояния идеального одноатомного газа. Газ отдал в этом процессе количество теплоты 80 кДж. Масса газа не менялась. Определите работу, совершённую внешними силами над газом в этом процессе, если р1 = 80 кПа, р2 = 200 кПа, Т0 =300 К.
10. С постоянной массой идеального одноатомного газа происходит циклический процесс 1−2−3−4−1, p–V-диаграмма которого представлена на рисунке. Максимальная температура газа в этом процессе составляет 400 К. На основании анализа этого циклического процесса выберите все верные утверждения.
1) Работа, совершённая газом при его изобарическом расширении, равна 200 Дж.
2) Количество вещества газа, участвующего в циклическом процессе, больше 0,45 моль.
3) Работа, совершённая над газом при его изобарическом сжатии, равна 200 Дж.
4) Изменение внутренней энергии газа в процессе 1–2–3–4–1 равно нулю.
5) Количество теплоты, переданное газу при изохорическом нагревании, равно 400 Дж.
11. В закрытом сосуде под подвижным поршнем находятся влажный воздух и немного воды. Перемещая поршень, объём сосуда медленно увеличивают при постоянной температуре. Как изменяются в этом процессе относительная влажность воздуха и концентрация пара? Известно, что в конечном состоянии в сосуде остаётся вода. Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
12. Участок электрической цепи состоит из трёх резисторов, соединённых так, как показано на рисунке. Сила тока I = 3 А. Сопротивления резисторов равны R1 = 20 Ом и R2 = 30 Ом. Каким должно быть сопротивление резистора R, чтобы сила текущего через него тока была равна 2 А?
13. На рисунке показан график зависимости магнитного потока Φ, пронизывающего проводящий контур, от времени t. Сопротивление контура равно 5 Ом. Чему равна сила тока, текущего в контуре, в промежутке времени от 0 до 10 с?
15. Две маленькие закреплённые бусинки, расположенные в точках А и В, несут на себе заряды +q > 0 и +4q соответственно (см. рисунок). Расстояние от точки С до точки А в два раза меньше, чем расстояние от точки С до точки В: СВ = 2 АС . Выберите все верные утверждения, соответствующие приведённым данным.
1) Модуль силы Кулона, действующей на бусинку в точке А, в 4 раза больше, чем модуль силы Кулона, действующей на бусинку в точке В.
2) Если бусинки соединить тонким проводником, то они будут притягиваться друг к другу.
3) Напряжённость результирующего электростатического поля в точке С равна нулю.
4) Если бусинки соединить стеклянной палочкой, то их заряды не изменятся.
5) Если бусинку с зарядом +4q заменить на бусинку с зарядом –4q, то напряжённость результирующего электростатического поля в точке С будет направлена вправо.
16. В первом опыте лазерный луч красного цвета падает перпендикулярно на дифракционную решётку, содержащую 50 штрихов на 1 мм. При этом на удалённом экране наблюдают дифракционную картину. Во втором опыте проводят эксперимент с тем же лазером, заменив решётку на другую, содержащую 100 штрихов на 1 мм, и оставив угол падения лазерного луча на решётку тем же. Как изменяются во втором опыте по сравнению с первым расстояние между дифракционными максимумами первого порядка на экране и количество наблюдаемых дифракционных максимумов? Для каждой величины определите соответствующий характер изменения:
- 1) увеличивается
- 2) уменьшается
- 3) не изменяется
17. В однородном вертикальном магнитном поле находится наклонная плоскость с углом α при основании. На этой плоскости закреплён П-образный проводник, по которому скользит вниз с постоянной скоростью V проводящая перемычка длиной L. Взаимное расположение наклонной плоскости, проводника и перемычки показано на рисунке. Сопротивление перемычки равно R, сопротивление П-образного проводника мало. Модуль индукции магнитного поля равен В. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
18. Какая доля радиоактивных ядер (в процентах от первоначального числа ядер) остаётся нераспавшейся через интервал времени, равный двум периодам полураспада?
19. В опыте по изучению фотоэффекта металлическая пластина облучалась светом с частотой ν. Работа выхода электронов из металла равна Авых. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать (h – постоянная Планка, с – скорость света в вакууме, me – масса электрона). К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
20. Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.
- 1) При равномерном прямолинейном движении за любые равные промежутки времени тело совершает одинаковые перемещения.
- 2) Средняя кинетическая энергия теплового движения молекул гелия уменьшается при увеличении абсолютной температуры газа.
- 3) В однородном электростатическом поле работа по перемещению электрического заряда между двумя положениями в пространстве не зависит от траектории.
- 4) При переходе электромагнитной волны из воды в воздух период колебаний вектора напряжённости электрического поля в волне уменьшается.
- 5) При испускании протона электрический заряд ядра уменьшается.
21. Даны следующие зависимости величин:
- А) зависимость модуля импульса материальной точки от её кинетической энергии при неизменной массе;
- Б) зависимость количества теплоты, выделяющегося при конденсации пара, от его массы;
- В) зависимость периода колебаний силы тока в идеальном колебательном контуре от индуктивности катушки.
Установите соответствие между этими зависимостями и графиками, обозначенными цифрами 1–5. Для каждой зависимости А–В подберите соответствующий вид графика и запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
22. Для определения массы порции подсолнечного масла ученик измерил её объём с использованием мерного цилиндра и получил результат: V = (12 ±1) см3 . Чему равна масса данной порции масла с учётом погрешности измерений?
23. Ученик изучает свойства силы трения скольжения. В его распоряжении имеются установки, состоящие из горизонтальной опоры и сплошного бруска. Площадь соприкосновения бруска с опорой при проведении всех опытов одинакова. Параметры установок приведены в таблице. Какие из этих установок нужно использовать для того, чтобы на опыте обнаружить зависимость коэффициента трения от модуля силы нормального давления тела на опору?
24. В боковой стенке покоящейся на столе бутылки проделано маленькое отверстие, в которое вставлена затычка. В бутылку налита вода, а горлышко бутылки закрыто резиновой пробкой, через которую пропущена вертикальная тонкая трубка. Нижний конец трубки находится выше отверстия в стенке бутылки, но ниже поверхности воды, а верхний конец сообщается с атмосферой (см. рис.). Затычку из отверстия в боковой стенке вынимают, и вода вытекает из бутылки через отверстие. При этом через трубку в бутылку входят пузырьки воздуха. Затем трубку начинают медленно опускать вниз и делают это до тех пор, пока нижний конец трубки не окажется на одном уровне с отверстием. Опишите, как будет изменяться скорость вытекания воды из отверстия по мере опускания трубки. Считайте, что уровень воды всегда находится выше нижнего конца трубки и выше отверстия в стенке. Ответ обоснуйте, указав, какие физические закономерности Вы использовали для объяснения.
25. В механической системе, изображённой на рисунке, все блоки, пружины и нити невесомые, нити нерастяжимые, трения в осях блоков нет, все участки нитей, не лежащие на блоках, вертикальны. Известно, что после подвешивания груза массой M = 40 кг к оси самого правого блока левая пружина в состоянии равновесия растянулась на величину Δx1 = 10 см. Найдите коэффициент жёсткости k1 левой пружины.
26. В центре металлической сферической оболочки толщиной 0,5 см поместили точечный заряд q = 2 мкКл, а на её внешнюю поверхность радиусом R = 10 см – заряд Q = – 1 мкКл. Найдите для равновесного состояния модуль напряжённости E электрического поля на расстоянии r = 1 м от центра оболочки и укажите, куда направлен вектор E – к центру оболочки или от неё.
27. В большом помещении с размерами 6 × 10 × 3 м3 в зимние холода при температуре Т1 парциальное давление водяного пара в воздухе составляло pп1 = 700 Па, а относительная влажность воздуха равнялась при этом φ1 = 50 %. После обогрева помещения температура в нём поднялась до значения T2 = 25 °С, а относительная влажность снизилась до φ2 = 25 %. Используя приведённый на рисунке график, найдите, как и на сколько в результате обогрева изменилась масса m паров воды в данном помещении.
28. Иногда для измерения индукции магнитного поля используют следующий способ: маленькую плоскую круглую катушку с большим числом витков быстро вводят в область измеряемого поля так, что её плоскость перпендикулярна линиям индукции. Катушка присоединена к входным клеммам баллистического гальванометра, который может измерять электрический заряд Δq, протекший по образовавшейся замкнутой цепи за время ввода измерительной катушки в исследуемое магнитное поле. Этот заряд связан с изменением магнитного потока Ф через катушку, поэтому данный гальванометр часто используют в качестве «флюксметра». Зная поток магнитной индукции и параметры катушки, можно найти величину В проекции индукции на ось катушки. Пусть измеренное таким способом значение В = 0,5 Тл, входное сопротивление гальванометра rф = 0,1 кОм, сопротивление измерительной катушки rк = 900 Ом, диаметр её витков d = 1 см. Определите число N витков в катушке, если протекший через цепь суммарный заряд qΣ = 15 мкКл.
29. Вдоль оптической оси тонкой выпуклой собирающей линзы распространяется в воздухе параллельный приосевой пучок света, собирающийся в точку справа от неё на расстоянии F1. Линза изготовлена из стекла с показателем преломления n1 = 1,4 и ограничена справа и слева сферическими поверхностями радиусами R1 = 15 см. На какое расстояние и в какую сторону сместится точка схождения лучей этого пучка, если заменить линзу на другую, с показателем преломления стекла n2 = 1,6 и радиусами поверхностей R2 = 24 см? Положения обеих линз относительно пучка света одинаковые. Все углы падения и преломления можно считать малыми и использовать для них приближённую формулу sin α ≈ α.
30. На даче у школьника на горизонтальном полу террасы стояла пластмассовая кубическая ёмкость для воды, иногда протекающей с крыши. Когда ёмкость заполнилась наполовину, дедушка попросил внука вылить воду из неё, наклонив вокруг одного из нижних рёбер куба, чтобы вода переливалась через соседнее верхнее ребро. Какую работу А совершил внук к моменту начала вытекания воды из ёмкости, если процесс подъёма был очень медленным, так что поверхность воды всё время оставалась горизонтальной? Объём воды вначале был равен V = 108 л, квадратные стенки ёмкости и её днище тонкие, однородные, массой m = 4 кг каждая (сверху ёмкость открыта). Сделайте рисунки с указанием положения центров масс воды, днища и стенок ёмкости до начала наклона ёмкости и в момент, когда вода начинает выливаться. Обоснуйте применимость используемых законов к решению задачи.
Вариант ФИ2210402 с ответами
1. Два маленьких тела, находившиеся в состоянии покоя, одновременно начинают двигаться из одной точки по плоскости YOX с разными по модулю постоянными ускорениями. На рисунке изображены векторы 1 a и 2 a ускорений этих тел (масштабы координатной сетки вдоль горизонтальной и вертикальной осей одинаковы). Чему равно отношение путей S1/S2, пройденных этими телами за первые 3 секунды их движения?
2. Ускорение свободного падения на поверхности Земли в 2,65 раза больше, чем на поверхности Марса. Вторая космическая скорость для Земли в 2,24 раза больше, чем для Марса. Во сколько раз радиус Земли больше радиуса Марса? Ответ округлите до целого числа.
3. На горизонтальном столе лежит лист бумаги, на котором нарисован равнобедренный треугольник ABC с основанием BC. Длина боковой стороны этого треугольника 18 см, угол при основании 30°. В его вершинах расположены одинаковые маленькие тяжёлые бусинки. На каком расстоянии от вершины A расположен центр тяжести системы, состоящей из этих трёх бусинок?
4. Небольшая шайба массой 100 г соскальзывает с наклонной плоскости с углом при основании 45°. Сопротивление воздуха пренебрежимо мало. В таблице приведены значения модуля скорости V шайбы в различные моменты времени t. Выберите все верные утверждения о результатах этого опыта на основании данных, содержащихся в таблице.
- 1) Между шайбой и плоскостью есть сухое трение.
- 2) Модуль ускорения шайбы приблизительно равен 7 м/с2 .
- 3) За первую секунду движения шайба прошла путь менее 2 м.
- 4) В момент времени t = 0,6 с модуль импульса шайбы примерно равен 0,36 кг⋅м/с.
- 5) Если в момент времени t = 1,2 с шайба столкнётся с абсолютно неупругим препятствием, то выделится количество теплоты ≈ 2,6 Дж.
5. На двух узких опорах покоится тяжёлая горизонтальная однородная доска. На доске посередине между опорами лежит гиря. Гирю перекладывают так, что она оказывается лежащей на доске ближе к правой опоре. Как после перекладывания гири изменяются модуль силы реакции левой опоры и момент силы тяжести гири относительно правой опоры? Для каждой величины определите соответствующий характер изменения:
- 1) увеличивается
- 2) уменьшается
- 3) не изменяется
6. На горизонтальном столе установлена в вертикальном положении лёгкая пружина жёсткостью k. Её нижний конец прикреплён к столу, а к верхнему концу прикреплена горизонтальная платформа массой M. На высоте H над платформой удерживают маленький пластилиновый шарик массой m. Шарик отпускают без начальной скорости, после чего он свободно падает и прилипает к покоившейся платформе. В результате этого платформа с шариком начинают совершать колебания, в ходе которых ось пружины остаётся вертикальной, а платформа не касается стола. Установите соответствие между физическими величинами и формулами, выражающими их в рассматриваемой задаче (g – ускорение свободного падения). К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
7. В сосуде объёмом 8,31 л находится 0,35 моля идеального газа при давлении 100 кПа. Газ сначала изотермически расширяют в 2 раза, а затем изобарически нагревают на 24 К. Чему равен объём газа в конечном состоянии?
8. На рисунке приведена зависимость температуры t однородного твёрдого тела массой 5 кг от времени τ в процессе нагревания. Чему равна удельная теплоёмкость вещества этого тела? Подводимую к телу тепловую мощность можно считать постоянной и равной 520 Вт.
9. На Т–V-диаграмме показан процесс изменения состояния идеального одноатомного газа. Газ получил в этом процессе количество теплоты 120 кДж. Масса газа не менялась. Определите работу, совершённую газом в этом процессе, если V1 = 8 л, V2 = 20 л, Т0 = 300 К.
10. С постоянной массой идеального одноатомного газа происходит циклический процесс 1−2−3−4−1, p–V-диаграмма которого представлена на рисунке. Максимальная температура газа в этом процессе составляет 600 К. На основании анализа этого циклического процесса выберите все верные утверждения.
- 1) Работа, совершённая газом при его изобарическом расширении, равна 400 Дж.
- 2) Количество вещества газа, участвующего в циклическом процессе, больше 0,45 моля.
- 3) Суммарное количество теплоты, которым газ обменялся с окружающими телами в процессе 1–2–3–4–1, равно 200 Дж.
- 4) Изменение внутренней энергии газа в процессе 4–1 равно 600 Дж.
- 5) Температура газа в состоянии 4 равна 225 К.
11. В закрытом сосуде под подвижным поршнем находятся влажный воздух и немного воды. Перемещая поршень, объём сосуда медленно уменьшают при постоянной температуре. Как изменяются в этом процессе относительная влажность воздуха и плотность пара? Для каждой величины определите соответствующий характер изменения:
- 1) увеличивается
- 2) уменьшается
- 3) не изменяется
12. Участок электрической цепи состоит из трёх резисторов, соединённых так, как показано на рисунке. Сила тока I = 6 А. Сопротивления резисторов равны R1 = 10 Ом и R2 = 30 Ом. Каким должно быть сопротивление резистора R, чтобы сила тока, текущего через него, была равна 2 А?
13. На рисунке показан график зависимости магнитного потока Φ, пронизывающего проводящий контур, от времени t. Сопротивление контура равно 3 Ом. Чему равна сила тока, текущего в контуре в промежутке времени от 10 до 20 с?
14. Сила тока i в идеальном колебательном контуре меняется со временем t по закону 0,02cos(5 10 ) 6 i = ⋅ t , где все величины выражены в единицах СИ. Чему равен максимальный заряд одной из пластин конденсатора, включённого в этот колебательный контур?
15. Две маленькие закреплённые бусинки, расположенные в точках А и В, несут на себе заряды +q > 0 и –4q соответственно (см. рисунок). Точка С расположена посередине отрезка АВ. Выберите все верные утверждения, соответствующие приведённым данным.
- 1) Сила Кулона, действующая на бусинку в точке А равна по модулю силе Кулона, действующей на бусинку в точке В.
- 2) Если бусинки соединить проводником, то они станут отталкиваться друг от друга.
- 3) Напряжённость результирующего электростатического поля в точке С направлена влево.
- 4) Если бусинки соединить стеклянной палочкой, то их заряды станут одинаковыми.
- 5) Если бусинку с зарядом –4q заменить на бусинку с зарядом +3q, то модуль напряжённости результирующего электростатического поля в точке С уменьшится в 2,5 раза.
16. В первом опыте лазерный луч красного цвета падает перпендикулярно на дифракционную решётку, содержащую 100 штрихов на 1 мм. При этом на удалённом экране наблюдают дифракционную картину. Во втором опыте проводят эксперимент с тем же лазером, заменив решётку на другую, содержащую 50 штрихов на 1 мм, и оставив угол падения лазерного луча на решётку тем же. Как изменяются во втором опыте по сравнению с первым расстояние между дифракционными максимумами второго порядка на экране и угол, под которым наблюдается первый дифракционный максимум? Для каждой величины определите соответствующий характер изменения:
- 1) увеличивается
- 2) уменьшается
- 3) не изменяется
17. В однородном вертикальном магнитном поле находится наклонная плоскость с углом α при основании. На этой плоскости закреплён П-образный проводник, по которому скользит вниз с постоянной скоростью V проводящая перемычка длиной L. Взаимное расположение наклонной плоскости, проводника и перемычки показано на рисунке. Сопротивление перемычки равно R, сопротивление П-образного проводника мало. Модуль индукции магнитного поля равен В. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
18. Какая доля радиоактивных ядер (в процентах от первоначального числа ядер) остаётся нераспавшейся через интервал времени, равный трём периодам полураспада?
19. В опыте по изучению фотоэффекта металлическая пластина облучалась светом с частотой ν. Работа выхода электронов из металла равна Авых. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать (h – постоянная Планка, с – скорость света в вакууме, me – масса электрона). К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
20. Выберите все верные утверждения о физических явлениях, величинах и закономерностях. Запишите цифры, под которыми они указаны.
- 1) При равномерном движении по окружности перемещение тела за один период обращения равно нулю.
- 2) При увеличении средней кинетической энергии теплового движения молекул гелия его давление в закрытом сосуде неизменного объёма уменьшается.
- 3) При движении заряда по окружности в однородном магнитном поле сила Лоренца, действующая на этот заряд, не совершает работу.
- 4) При переходе электромагнитной волны из воздуха в воду период колебаний вектора индукции магнитного поля в волне не изменяется.
- 5) При испускании нейтрона электрический заряд ядра увеличивается.
21. Даны следующие зависимости величин:
- А) зависимость кинетической энергии материальной точки от модуля её импульса при неизменной массе;
- Б) зависимость количества теплоты, выделяющегося при кристаллизации воды, от её массы;
- В) зависимость энергии конденсатора постоянной ёмкости от его заряда.
Установите соответствие между этими зависимостями и графиками, обозначенными цифрами 1–5. Для каждой зависимости А–В подберите соответствующий вид графика и запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
22. Для определения массы порции керосина ученик измерил её объём с использованием мерного цилиндра и получил результат: V = (30,0 ± 0,5) см3 . Чему равна масса данной порции керосина с учётом погрешности измерений?
23. Ученик изучает свойства силы трения скольжения. В его распоряжении имеются установки, состоящие из горизонтальной опоры и сплошного бруска. Площадь соприкосновения бруска с опорой при проведении всех опытов одинакова. Параметры установок приведены в таблице. Какие из установок нужно использовать для того, чтобы на опыте обнаружить зависимость коэффициента трения от материала опоры?
24. В боковой стенке покоящейся на столе бутылки проделано маленькое отверстие, в которое вставлена затычка. В бутылку налита вода, а горлышко бутылки закрыто резиновой пробкой, через которую пропущена вертикальная тонкая трубка. Нижний конец трубки находится ниже поверхности воды на уровне отверстия в стенке бутылки, а верхний конец сообщается с атмосферой (см. рис.). Затычку из отверстия в боковой стенке вынимают и начинают медленно поднимать трубку вверх. При этом вода вытекает из бутылки через отверстие, а через трубку в бутылку входят пузырьки воздуха. Опишите, как будет изменяться скорость вытекания воды из отверстия по мере поднимания трубки. Считайте, что уровень воды всегда находится выше нижнего конца трубки и выше отверстия в стенке. Ответ обоснуйте, указав, какие физические закономерности Вы использовали для объяснения.
25. В механической системе, изображённой на рисунке, все блоки, пружины и нити невесомые, нити нерастяжимые, трения в осях блоков нет, все участки нитей, не лежащие на блоках, вертикальны. Известно, что после подвешивания груза M к оси самого правого блока левая пружина, имеющая коэффициент жёсткости k1 = 500 Н/м, в состоянии равновесия растянулась на величину Δx1 = 10 см. На какую величину Δx2 удлинилась при этом правая пружина, если её коэффициент жёсткости равен k2 = 1000 Н/м?
26. В центре металлической сферической оболочки толщиной 0,2 см поместили точечный заряд q = 1 мкКл, а на её внешнюю поверхность радиусом R = 10 см – заряд Q = – 3 мкКл. Найдите для равновесного состояния модуль E напряжённости электрического поля на расстоянии r = 2 м от центра оболочки и укажите, куда направлен вектор E – к центру оболочки или от неё.
27. В большом помещении с размерами 5 × 10 м2 (пол) и 3,5 м (высота потолка) температура T1 во время зимних холодов понизилась, парциальное давление водяного пара в воздухе опустилось до значения pп1 = 600 Па, а относительная влажность воздуха равнялась при этом φ1 = 50 %. После обогрева помещения температура в нём поднялась до значения T2 = 24 °С, а относительная влажность снизилась до φ2 = 30 %. Используя приведённый на рисунке график, найдите, как и во сколько раз в результате обогрева изменилась масса m паров воды в данном помещении.
28. Иногда для измерения индукции магнитного поля используют следующий способ: маленькую плоскую круглую катушку с большим числом витков быстро вводят в область измеряемого поля так, что её плоскость перпендикулярна линиям индукции. Катушка присоединена к входным клеммам баллистического гальванометра, который может измерять электрический заряд Δq, протекший по образовавшейся замкнутой цепи за время ввода измерительной катушки в исследуемое магнитное поле. Этот заряд связан с изменением магнитного потока Ф через катушку, поэтому данный гальванометр часто используют в качестве «флюксметра». Зная поток магнитной индукции и параметры катушки, можно найти величину В проекции индукции на ось катушки. Пусть входное сопротивление гальванометра rф = 0,2 кОм, сопротивление измерительной катушки rк = 600 Ом, диаметр её витков d = 0,95 см, число витков в ней N = 300. Чему равен измеренный модуль индукции магнитного поля, если протекший через цепь суммарный заряд qΣ = 12 мкКл.
29. Вдоль оптической оси тонкой выпуклой собирающей линзы распространяется в воздухе параллельный приосевой пучок света, собирающийся в точку справа от неё на расстоянии F1. Линза изготовлена из стекла с показателем преломления n1 = 1,5 и ограничена справа и слева сферическими поверхностями радиусами R1 = 20 см. На какое расстояние сместится точка схождения лучей этого пучка, если заменить линзу на другую, с показателем преломления стекла n2 = 1,7 и радиусами поверхностей R2 = 16 см? Положения обеих линз относительно пучка света одинаковые. Все углы падения и преломления можно считать малыми и использовать для них приближённую формулу sinα ≈ α.
30. На даче у школьника на горизонтальном полу террасы стояла пластмассовая кубическая ёмкость для воды, иногда протекающей с крыши. Когда ёмкость заполнилась наполовину, дедушка попросил своего сильного внука вылить воду из неё, наклонив вокруг одного из нижних рёбер куба, чтобы вода переливалась через соседнее верхнее ребро. Оцените, на какую величину ∆E внук увеличит механическую энергию ёмкости с водой к моменту начала вытекания воды из ёмкости, если процесс подъёма был очень медленным, так что поверхность воды всё время оставалась горизонтальной? Объём воды вначале был равен V = 63 л, квадратные стенки ёмкости и её днище тонкие, однородные, массой m = 3 кг каждая (сверху ёмкость открыта). Сделайте рисунки с указанием положения центров масс воды, днища и стенок ёмкости до начала наклона ёмкости и в момент, когда вода начинает выливаться. Обоснуйте применимость используемых законов к решению задачи.
Попробуйте решить другие варианты
Статград ФИ2210301-ФИ2210304 физика 11 класс ЕГЭ 2023 варианты и ответы
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Задача 1
К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён массивный груз, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно (см. рисунок). Коэффициент трения груза по плоскости Груз смещают по горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно d = 15 см. Найдите массу m груза.
Решение
1. Начальная энергия системы равна потенциальной энергии растянутой пружины: После того, как пружину отпустили, она остановится в положении, при котором она сжата на величину
Тогда конечная энергия системы равна потенциальной энергии сжатой пружины:
Изменение полной энергии системы равно работе силы трения
где — модуль силы реакции опоры.
2. В момент, когда груз остановился, по второму закону Ньютона равнодействующая всех сил стала равна нулю. Пружина сжата, поэтому сила упругости пружины направлена вправо. Её уравновешивает сила трения покоя, которая направлена против возможного движения, причём эта сила максимальна, т. к. по условию начальное положение пружины соответствует максимальному растяжению пружины, при котором груз движется таким образом.
Запишем закон Ньютона для горизонтальной и вертикальной осей:
3. Подставим полученное выражение для в равенство из пункта 1:
После подстановки получим
Ответ:
Задача 2
Из пружинного пистолета выстрелили вертикально вниз в мишень, находящуюся на расстоянии 2 м от него. Совершив работу 0,12 Дж, пуля застряла в мишени. Какова масса пули, если пружина была сжата перед выстрелом на 2 см, а ее жесткость 100 Н/м?
Решение
Согласно закону сохранения механической энергии, имеем два равенства:
где и
— скорости летящей пули соответственно на высоте и непосредственно перед мишенью. Вся энергия подлетевшей к мишени пули потрачена на механическую работу, так что
Решая полученную систему уравнений, находим массу пули:
Задача 3
Небольшая шайба после толчка приобретает скорость v = 2 м/с и скользит по внутренней поверхности гладкого закрепленного кольца радиусом R = 0,14 м. На какой высоте h шайба отрывается от кольца и начинает свободно падать?
Решение
Согласно закону сохранения энергии:
, (1)
где — скорость шайбы в момент отрыва от кольца на высоте
.
В точке отрыва сила нормальной реакции опоры равна 0; . Центростремительное ускорение шайбы
найдём из второго закона Ньютона (см. рис.):
. (2)
. (3)
Объединяя (1), (2) и (3), получим:
м.
Ответ: 0,18.
Задача 4
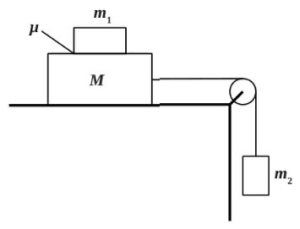
Грузы массами M = 1 кг и m связаны легкой нерастяжимой нитью, переброшенной через блок, по которому нить может скользить без трения (см. рис.). Груз массой М находится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту а = 30°, коэффициент трения = 0,3). Чему равно минимальное значение массы m, при котором система грузов еще не выходит из первоначального состояния покоя?
Решение
Если масса m достаточно мала, но грузы ещё покоятся, то сила трения покоя, действующая на груз массой М, направлена вверх вдоль наклонной плоскости. Запишем второй закон Ньютона для каждого из покоящихся тел в проекциях на оси введенной системы координат. На первое тело действуют сила тяжести, сила нормальной реакции опоры, сила натяжения нити и сила трения:
(ось направлена вниз вдоль наклонной плоскости);
(ось направлена вверх перпендикулярно наклонной плоскости).
На второе тело действуют сила тяжести и сила натяжения нити:
(ось направлена вертикально вниз).
Учитывая, что (нить легкая, между блоком и нитью трения нет), то
(сила трения покоя). Получим:
кг.
Ответ: 0,24.
Задача 5
Тело, брошено с поверхности земли со скоростью v под углом a к горизонту. Сопротивление воздуха пренебрежимо мало.
Установите соответствие между физическими величинами, характеризующими движение тела, и формулами, по которым их можно определить.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.

Решение
Рассмотрим динамику движения тела, брошенного под углом к горизонту с начальной скоростью
. В задаче нас интересует вертикальное движение тела.
Из рисунка видно, что проекция начальной скорости на ось Oy равна
.
Проекция ускорения равна
,
где м/с2 – ускорение свободного падения. Таким образом, скорость тела вдоль оси Oy будет меняться по закону
.
Можно заметить, что в точке максимального подъема скорость , получаем уравнение
То есть для буквы «А» соответствует формула под номером 4.
Для определения максимальной высоты , запишем формулу движения тела, подброшенного вертикально вверх:
и, учитывая, что ,
, а время для достижения максимальной высоты составляет
, получаем выражение:
.
То есть для буквы «Б» соответствует формула под номером 1.
Ответ: А4, Б1.
Задача 6
Воздушный шар объемом V = 2500 м3 с массой оболочки = 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры t1 нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой
= 200 кг? Температура окружающего воздуха t = 7 °С, его плотность
= 1,2 кг/м3. Оболочку шара считать нерастяжимой.
Решение
Шар взлетает, когда сила тяжести, действующая на него, равна силе Архимеда
, (1)
где m — масса воздуха в шаре. Из уравнения Менделеева-Клапейрона
,
, (2)
где ,
,
— молярная масса воздуха. Объединяя (1) и (2), получим:
К
соответственно °С.
Ответ: 350.
Задача 7
Брусок массой m1 = 500 г соскальзывает по наклонной плоскости с некоторой высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m2 = 300 г. Считая столкновение абсолютно неупругим, определите высоту h, если общая кинетическая энергия брусков после столкновения равна 2,5 Дж. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.
Решение
Кинетическая энергия брусков после столкновения где v — скорость системы после удара, определяемая из закона сохранения импульса на горизонтальном участке: m1v1 = (m1 + m2)v.
Исключая из системы уравнений скорость v, получим:
Кинетическая энергия первого бруска перед столкновением определяется из закона сохранения механической энергии при скольжении по наклонной плоскости: что даёт выражение
Подставляя значения масс и энергии из условия, получим численное значение h = 0,8 м
Ответ: h = 0,8 м.
Задача 8
Небольшой груз, прикрепленный к нити длиной l = 15 см, вращается вокруг вертикальной оси так, что нить отклоняется от вертикали на угол a = 60°. С какой скоростью движется груз?
Решение
На груз действуют сила натяжения нити и сила тяжести
, как указано на рисунке.
В инерциальной системе отсчёта, связанной с Землёй, ускорение тела определяется вторым законом Ньютона:
Здесь — центростремительное ускорение. Решая полученную систему, получим:
м/с.
Ответ: 1,5.
Задача 9
Камень массой m = 4 кг падает под углом a = 30° к вертикали со скоростью 10 м/с в тележку с песком общей массой M = 16 кг, покоящуюся на горизонтальных рельсах. Определите скорость тележки с камнем после падения в нее камня.
Решение
Общая инерция камня, падающего в тележку, равна . Величина инерции, в горизонтальном направлении от падения камня составит
. Тогда из закона сохранения инерции, учитывая, что тележка вначале была неподвижной, а после падения в нее камня увеличила свою массу на массу камня, получаем
,
откуда
и

Ответ: 1.
Задача 10
Два груза одинаковой массы М, связанные нерастяжимой и невесомой нитью, движутся прямолинейно по гладкой горизонтальной поверхности под действием горизонтальной силы F, приложенной к одному из грузов (см. рис.). Минимальная сила F, при которой нить обрывается, равна 12 Н. При какой силе натяжения обрывается нить?
Решение
Сила, под действием которой движутся грузы массой M – это равнодействующая, то есть учитывающая силу трения. Следовательно, из второго закона Ньютона можно записать , где
— ускорение, с которым движутся грузы. Сила натяжения нити T создается последним грузом, который перемещается с тем же ускорением
, но имеет массу M, т.е.
. Выражая ускорение как
, получаем силу натяжения, равную
Н.
Ответ: 6.
Задача 11
Груз, лежащий на столе, связан легкой нерастяжимой нитью, переброшенной через идеальный блок, с грузом массой 0,25 кг. На первый груз действует горизонтальная постоянная сила F, равная 9 Н (см. рис.). Второй груз движется с ускорением 2 м/с2, направленным вверх. Трением между грузом и поверхностью стола пренебречь. Какова масса первого груза?
Решение
На второй груз действует сила тяжести и противоположная сила тяги первого груза
Н (трение здесь не учитывается). Таким образом, для системы из двух грузов массами
и
можем записать
,
где — масса первого груза. Отсюда получаем:
Подставляем числовые значения, находим
кг.
Ответ: 3.
Задача 12
Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика непосредственно перед первым ударом направлена вертикально вниз и равна 1 м/с.
Решение
Выберем следующую систему координат: ось направим вдоль плоскости, а ось
— перпендикулярно ей. Тогда кинематические уравнения движения шарика имеют вид:
В момент второго соударения шарика с плоскостью
Решая систему уравнений, получаем:
и
Из рисунка видно, что
Ответ:
Задача 13
На гладкой горизонтальной поверхности стола покоится горка с двумя вершинами, высоты которых h и 5/2*h (см. рисунок). На правой вершине горки находится шайба. От незначительного толчка шайба и горка приходят в движение, причём шайба движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. Скорость шайбы на левой вершине горки оказалась равной v. Найдите отношение масс шайбы и горки.
Решение
На систему тел «шайба + горка» действуют внешние силы (тяжести и реакции стола), направленные по вертикали, поэтому проекция импульса системы на горизонтальную ось Ох системы отсчёта, связанной со столом, сохраняется.
В начальный момент , а в момент
. Из закона сохранения импульса
получим:
, где m — масса шайбы, М — масса горки.
Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение
.
Решение системы дает отношение масс
.
Ответ: .
Задача 14
Снаряд, движущийся со скоростью v0 разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая движется в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ∆E. Скорость осколка, движущегося вперёд по направлению движения снаряда, равна v1. Найдите массу m осколка.
Решение
Введём обозначение: v2 — модуль скорости летящего назад осколка снаряда. Система уравнений для решения задачи:
Выразим v2 из первого уравнения: — и подставим во второе уравнение. Получим:
. Отсюда следует:

Ответ: 
Задача 15
Снаряд массой 2m разрывается в полёте на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ∆Е. Модуль скорости осколка, движущегося по направлению движения снаряда, равен v1, а модуль скорости второго осколка равен v2. Найдите ∆Е.
Решение
Введём обозначение: v0 — модуль скорости снаряда до разрыва. Система уравнений для решения задачи:
Выразим v0 из первого уравнения: и подставим во второе уравнение. Получим:
.
Отсюда следует:
.
Ответ: .
Задача 16
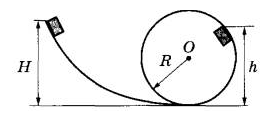
При выполнении трюка «Летающий велосипедист» гонщик движется по гладкому трамплину под действием силы тяжести, начиная движение из состояния покоя с некоторой высоты (см. рисунок). На краю трамплина скорость гонщика направлена под углом α = 60° к горизонту. Пролетев по воздуху, он приземляется на горизонтальный стол, поднявшись в полёте на высоту h над краем трамплина. С какой высоты H начинал движение гонщик?
Решение
Применим закон сохранения энергии и найдём скорость велосипедиста при отрыве от трамплина.
Рассмотрим проекции скорости на горизонтальную и вертикальную оси:
В тот момент, когда велосипедист достигнет наивысшей точки полёта вертикальная проекция его скорости станет равной нулю, при этом в горизонтальном направлении он пролетит половину пути. Найдём время, за которое велосипедист достигнет наивысшей точки.
Координата зависит от времени по закону
Значит, максимальная высота полёта велоспедиста
Откуда
Ответ:
Задача 17
После толчка льдинка закатилась в яму с гладкими стенками, в которой она может двигаться практически без трения. На рисунке приведен график зависимости энергии взаимодействия льдинки с Землей от её координаты в яме.
В некоторый момент времени льдинка находилась в точке А с координатой и двигалась влево, имея кинетическую энергию, равную 2 Дж. Сможет ли льдинка выскользнуть из ямы? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.
Решение
1) Льдинка сможет выскользнуть из ямы через ее правый край.
2) Трения при движении льдинки нет, поэтому ее механическая энергия сохраняется. Запас кинетической энергии льдинки в точке A позволяет ей подняться до уровня, где ее потенциальная энергия составит 4 Дж.
3) Левый край ямы поднят до большей высоты. Следовательно, этого края льдинка не достигнет и заскользит вправо. Правый же край ямы ниже: на верху этого края потенциальная энергия льдинки меньше 4 Дж. Поэтому льдинка выскользнет из ямы через правый край.
Задача 18
Гладкий клин массой M с углом при основании стоит на горизонтальной плоскости, часть которой под ним и левее — гладкая, а часть — справа от него — шероховатая (см. рис.). На вершине клина, на высоте H над плоскостью находится маленький брусок массой m, коэффициент трения которого о шероховатую часть плоскости равен
Брусок отпускают без начальной скорости, он скатывается по клину и далее скользит по шероховатой плоскости и останавливается на некотором расстоянии L по горизонтали от своего начального положения. Найдите это расстояние L, если в точке перехода с клина на плоскость есть гладкое закругление, так что скорость бруска при переходе с клина на плоскость не уменьшается.
Решение
При соскальзывании бруска с клина выполняются законы сохранения горизонтальной проекции импульса и механической энергии данной системы тел:
где v и V — скорости бруска и клина, соответственно, после соскальзывания бруска с клина. Из этих уравнений следует, что скорость бруска перед его попаданием на шероховатый участок плоскости равна:
До попадания на этот участок брусок сдвинется из начального положения по горизонтали без трения на расстояние равное, очевидно, длине основания клина, а затем пройдёт по шероховатой плоскости расстояние
на котором его кинетическая энергия будет израсходована на работу против силы сухого трения скольжения. По закону Амонтона — Кулона эта сила равна
так как сила N давления бруска на неподвижную горизонтальную плоскость равна mg. Таким образом,
и
Искомое расстояние L в результате равно сумме l1 и l2:
Ответ:
Задача 19
В системе, изображённой на рисунке, трения нет, блоки невесомы, нить невесома и нерастяжима, m1 = 2 кг, m2 = 4 кг, m3 = 1 кг. Найдите модуль и направление ускорения груза массой m3.
Решение
1. Введём на рисунке неподвижную систему координат, у которой ось x горизонтальна и направлена вправо, а ось y направлена вертикально вниз. Обозначим также силы, определяющие ускорения тел вдоль направлений их движения: силу T натяжения нити, которая, как следует из условия задачи, постоянна по модулю вдоль всей нити, и силу тяжести
2. Записывая второй закон Ньютона в проекциях на оси x и y для трёх грузов, имеем:
3. Поскольку нить нерастяжима, из постоянства её длины получаем следующее соотношение для координат грузов:
Отсюда следует связь между ускорениями грузов:
4. Решая полученную систему уравнений, находим модуль искомого ускорения:
вектор направлен вниз.
Ответ: вектор
направлен вниз.
Задача 20
К двум вертикально расположенным пружинам одинаковой длины подвесили однородный стержень длиной L = 30 см. Если к этому стержню подвесить груз массой m = 3 кг на расстоянии d = 5 см от правой пружины, то стержень будет расположен горизонтально, и растяжения обеих пружин будут одинаковы (см. рисунок). Жёсткость левой пружины в 2 раза меньше, чем правой. Чему равна масса стержня М? Сделайте рисунок с указанием используемых в решении сил.
Решение
1. Укажем на рисунке силы действующие на стержень. Приравняем моменты сил, действующих на стержень, относительно центра стержня, т.е. точки А:
Учтем, что стержень расположен горизонтально, т.е. удлинения пружин равны, а также, что жесткость правой пружины в два раза больше левой:
2. Приравняем моменты сил, действующих на стержень, относительно точки Б, которая находится в месте крепления правой пружины:
3. Найдем массу стержня:
Ответ:
Задача 21
Найдите модуль ускорения a груза массой m в системе, изображённой на рисунке. Трения нет, блоки невесомы, нити лёгкие и нерастяжимые, их участки, не лежащие на блоках, вертикальны, масса второго груза M, ускорение свободного падения равно g.
Решение
Введём координатную ось Х, направленную вниз, и отметим на ней координаты грузов М и m: xM и xm (см. рис.). Пронумеруем блоки цифрами 1, 2, 3 и укажем на рисунке силы натяжения нитей и силы тяжести, действующие на грузы. Согласно условию, в силу невесомости нитей и блоков, а также отсутствия сил трения, первая нить, охватывающая блоки 1 и 2, натянута с силой T, а вторая — с силой 2T, так что на груз m действует направленная вверх сила 4T. Если сместить груз М вдоль оси Х вниз на расстояние ΔxM, то в силу нерастяжимости нитей блок 2 сместится, как следует из рисунка, на −ΔxM/2, а блок 3 и груз m — на Δxm = −ΔxM/4. Таким образом, ΔxM + 4Δxm = 0.
Отсюда получаем уравнение кинематической связи: A + 4a = 0, где A и a — проекции ускорений грузов М и m на ось Х. Уравнения движения грузов (второй закон Ньютона) в проекциях на ось Х имеют вид: МA = Мg – T, ma = mg – 4T. Решая полученную систему из трех уравнений, находим, что модуль ускорения груза М равен:
Ответ:
Задача 22
Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рисунок). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 45°. Найдите модуль силы действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
Решение
1. Изобразим на рисунке силы, действующие на стержень, и систему координат Оху.
Здесь — сила натяжения нити,
— сила тяжести,
и
— вертикальная и горизонтальная составляющие силы, действующей на стержень со стороны шарнира.
2. В положении равновесия равны нулю сумма моментов сил, действующих на стержень, относительно оси, проходящей через точку А перпендикулярно плоскости рисунка, сумма горизонтальных и сумма вертикальных составляющих сил, действующих на стержень:
где
— длина стержня; (1)
(2)
(3)
3. Модуль силы реакции шарнира
Из (1) получим Окончательно
Ответ:
Задача 23
Из двух ровных досок сделан желоб, представляющий собой двугранный угол с раствором Желоб закреплен так, что его ребро горизонтально, а доски симметричны относительно вертикали. В желобе на боковой поверхности лежит цилиндр массой
Коэффициент трения между досками и цилиндром равен
К торцу цилиндра приложена горизонтально направленная сила
Найдите модуль ускорения цилиндра.
Решение
Изобразим вид на желоб со стороны торца цилиндра. На цилиндр в плоскости чертежа действуют направленная вниз сила тяжести
и две равные по модулю силы реакции
досок, направленные перпендикулярно стенкам желоба. Так как цилиндр не движется в вертикальном направлении, то, в соответствии со вторым законом Ньютона, сумма проекций этих трех сил на вертикаль равна нулю:
где
Отсюда В горизонтальном направлении (вдоль желоба) на цилиндр действуют сила
а также, в противоположном направлении, две силы сухого трения
Предположим, что цилиндр будет двигаться по желобу. Тогда по закону Амонтона — Кулона для силы сухого трения скольжения можно записать:
Записывая второй закон Ньютона в проекции на горизонтальную ось, направленную вдоль ребра желоба, получим:
где — модуль искомого ускорения цилиндра. Заметим, что
Это означает, что приложенная к торцу цилиндра сила превышает силу трения покоя, то есть цилиндр и в самом деле будет скользить вдоль желоба.
Следовательно, Подставляя числовые данные и проверяя размерность, окончательно получим:
Ответ:
Задача 24
Равносторонний треугольник, состоящий из трёх жёстких лёгких стержней, может вращаться без трения вокруг горизонтальной оси, совпадающей с одной из его сторон. В точке пересечения двух других его сторон к треугольнику прикреплён массивный грузик (см. рисунок). Как и во сколько раз изменится период малых колебаний грузика около его положения равновесия, если ось вращения наклонить под углом к горизонту?
Решение
Обозначим расстояние от оси вращения треугольника до грузика через Тогда период колебаний при горизонтальном положении оси равен, очевидно,
После наклона оси на угол возвращающая сила при отклонении треугольника от положения равновесия уменьшится: составляющая силы тяжести вдоль оси, равная
(здесь
— масса грузика), будет компенсироваться силами реакции со стороны подшипников, в которых закреплена эта ось, а в направлении, перпендикулярном оси, будет действовать эффективная «сила тяжести», равна
Поэтому период малых колебаний грузика при наклоненной оси будет равен
Таким образом, период колебаний увеличится в раз.
Ответ: период колебаний увеличится в раз.
Задача 25
На гладкой горизонтальной плоскости лежат два груза массами и
соединённые невесомой нерастяжимой нитью, перекинутой через два неподвижных (А и В) и один подвижный (О) невесомые блоки, как показано на рисунке. Оси блоков горизонтальны, трения в осях блоков нет. К оси О подвижного блока приложена направленная вертикально вниз сила F = 4 Н. Найдите ускорение этой оси. Сделайте схематический рисунок с указанием сил, действующих на грузы и блок.
Решение
Нарисуем силы Т натяжения нити, одинаковые, в силу условия задачи, вдоль всей нити и действующие на грузы и блок О (см. рисунок). Введём систему координат XY, как показано на рисунке, и запишем уравнения движения грузов в проекции на ось X:
В силу невесомости блока О имеем или
В силу нерастяжимости нити (длиной L) и неподвижности блоков А и В (их координаты и
постоянны) имеется следующая кинематическая связь между координатами
и
грузов и координатой
блока О (здесь
— радиус блоков А и В, R — радиус блока О):
или
и значит
Решаем записанную систему уравнений и получаем ответ:
Ответ:
Задача 26
Два вращающихся вала соединены замкнутым ремнём, который не проскальзывает относительно валов. Радиус первого вала равен R, радиус второго вала равен 2R. Чему равно отношение угловой скорости точки A к угловой скорости вращения первого вала
Решение
Скорость движения точек первого вала, находящихся на расстоянии от его центра, даётся формулой
Угловая скорость вращения точки А равна угловой скорости вращения второго вала. Валы связаны ремнём, поэтому скорости ободов
у валов одинаковы, а их угловые скорости
В итоге получаем
Ответ: 0,5.
Задача 28
Два велосипедиста совершают кольцевую гонку с одинаковой угловой скоростью. Положения и траектории движения велосипедистов показаны на рисунке. Чему равно отношение центростремительных ускорений велосипедистов ?
Решение
При движении по окружности угловая и линейная
скорости тела связаны с радиусом окружности
соотношением:
Центростремительное ускорение равно
Поскольку велосипедисты едут с одинаковым угловыми скоростями, для отношения центростремительных ускорения велосипедистов имеем:
Ответ: 2.
Задача 29
Прибор наблюдения обнаружил летящий снаряд и зафиксировал его горизонтальную координату и высоту
м над Землёй (см. рисунок). Через 3 с снаряд упал на Землю и взорвался на расстоянии
м от места его обнаружения. Известно, что снаряды данного типа вылетают из ствола пушки со скоростью 800 м/с. Какова была максимальная высота Н траектории снаряда, если считать, что сопротивление воздуха пренебрежимо мало? Пушка и место взрыва находятся на одной горизонтали.
Первое решение
Найдём горизонтальную скорость снаряда:
Найдём вертикальную проекцию скорости снаряда в момент обнаружения:
Определим, за какое время снаряд долетел из верхней точки траектории в точку, в которой был зафиксирован:
Таким образом, время опускания снаряда составляет
Таким образом, максимальная высота снаряда:
Второе решение
Найдём горизонтальную скорость снаряда: эта скорость остается постоянной на протяжении всего полета. Определим величину вертикальной проекции скорости в начальный момент:
Используя формулу для максимальной высоты брошенного под углом к горизонту тела, получаем:
Ответ: около 16 км.
Задача 30
К концу вертикального стержня привязана лёгкая нерастяжимая нить с маленьким грузиком на конце. Грузик раскрутили на нити так, что она отклонилась от вертикали на угол α = 30º (см. рисунок). Как и во сколько раз надо изменить угловую скорость ω вращения грузика вокруг стержня для того, чтобы этот угол стал равным β = 60º?
Решение
1. Обозначим силу натяжения нити T, массу грузика m, длину нити l, радиус окружности, по которой вращается грузик, R, и изобразим систему на рисунке (см. рисунок).
2. Запишем уравнение движения грузика по окружности вокруг стержня в проекциях на вертикальную ось и на радиус окружности с учётом выражения для центростремительного ускорения грузика:
,
.
3. Из написанных соотношений следует, что , а
.
4. Для того, чтобы угол отклонения нити стал равным β, угловая скорость вращения грузика должна увеличиться в
раза.
Ответ: 1,3 раза.
Задача 31
В аттракционе человек массой 80 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если при скорости 10 м/с, направленной вертикально вверх, сила нормального давления человека на сидение тележки равна 1 600 Н? Ускорение свободного падения равно
Задача 32
На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 45 с? Ответ выразите в м/с2.
Решение
Из графика видно, что скорость в интервале времени от 40 с до 50 с меняется линейно, значит, ускорение постоянно. На всём этом интервале времени ускорение такое же, как и в момент времени 45 с. Найдём это ускорение:
Ответ: 2.
Задача 32
Два небольших тела с массами 2 кг и 3 кг висят на разных концах невесомой нерастяжимой нити, перекинутой через гладкий неподвижный блок. Первое тело находится на высоте 40 см ниже второго. Тела пришли в движение без начальной скорости. Через какое время они окажутся на одной высоте? Сделайте схематический рисунок с указанием сил, действующих на тела. Обоснуйте применимость используемых законов к решению задачи.
Решение
Задача 33
Система грузов M, m1 и m2, показанная на рисунке, движется из состояния покоя. Поверхность стола — горизонтальная гладкая. Коэффициент трения между грузами M и m1 равен μ = 0,3. Грузы M и m2 связаны легкой нерастяжимой нитью, которая скользит по блоку без трения. Пусть M = 2,4 кг, m1 = m2 = m. При каких значениях m грузы M и m1 движутся как одно целое? Сделайте рисунок с указанием сил, действующих на грузы.
Решение
Задача 34
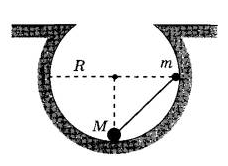
Небольшие шарики, массы которых m и M, соединены лёгким стержнем и помещены в гладкую сферическую выемку радиусом R = 20 см. В начальный момент шарики удерживаются в положении, изображённом на рисунке. Когда их отпустили без толчка, шарики стали скользить по поверхности выемки. Минимальная высота, на которой оказался шарик m в процессе движения, равна 4 см от нижней точки выемки. Определите отношение масс M и m.
Решение
Задача 35
Небольшой брусок массой m начинает соскальзывать с высоты H по гладкой горке, переходящей в мёртвую петлю (см. рисунок). Определите высоту отрыва бруска, если высота горки H. Радиус окружности R. Сделайте рисунок с указанием сил, поясняющий решение.
Решение
Направим ось Ох вдоль ускорения и пусть сила тяжести образует с этой осью угол α Запишем второй закон Ньютона для бруска на высоте h:
Выразим отсюда скорость бруска, учитывая, что и по третьему закону Ньютона
:
На высоте h брусок обладает как кинетической, так и потенциальной энергией. Из закона сохранения энергии найдём искомую высоту H:
откуда
Задача 36
В маленький шар массой M=100г, висящий на нити длиной l=50 см, попадает и застревает в нем пулька массой m=20г, летящая под углом 30 град к горизонту (см рисунок). Какую скорость v имела пуля перед попаданием в шар, если после соударения шар с застрявшей в нем пулей отклонился по вертикали на угол 60 град? Сопротивлением воздуха пренебречь. Какие законы вы использовали для описания взаимодействия пульки с шаром и подьема тел? Обоснуйте их применимость к данному случаю.
Решение
Задача 37
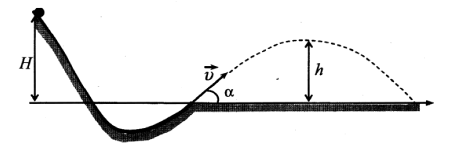
При выполнение трюка летающий велосипедист гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты H. На краю трамплина скорость гонщика направлена под таим углом к горизонту, что дальность его полета максимальна. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящейся на той же высоте, что и край трамплина. Какова высота полета h на этом трамплине? Сопротивлением воздуха и трением пренебречь.
Решение