При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
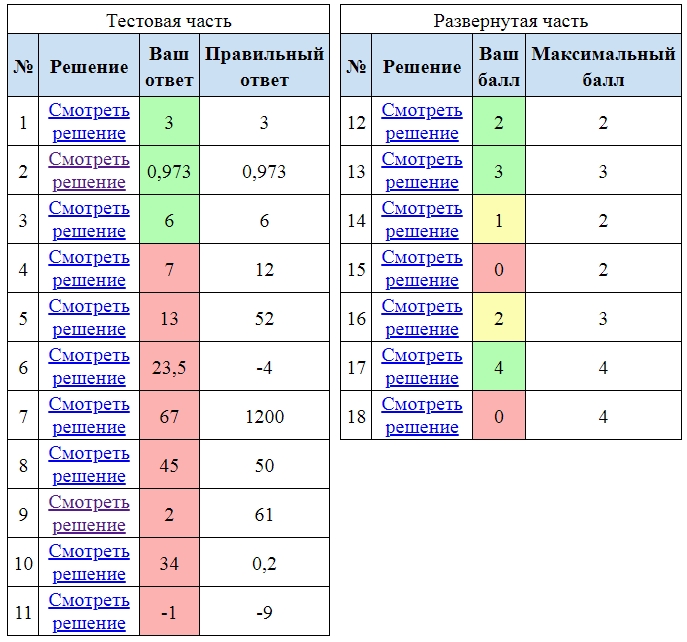
1
Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.
Ответ:
2
У Вити в копилке лежит 12 рублёвых, 6 двухрублёвых, 4 пятирублёвых и 3 десятирублёвых монеты. Витя наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 70 рублей.
Ответ:
3
4
5
6
На рисунке изображен график функции y = f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите
Ответ:
7
8
Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Ответ:
9
На рисунке изображён график функции вида где числа a, b, c и d — целые. Найдите
Ответ:
10
При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
В ответе укажите наименьшее необходимое количество выстрелов.
Ответ:
11
Найдите наименьшее значение функции на отрезке
Ответ:
12
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
13
Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник ABC с прямым углом C. Грань ACC1A1 является квадратом.
а) Докажите, что прямые CA1 и AB1 перпендикулярны.
б) Найдите расстояние между прямыми CA1 и AB1, если AC = 4, BC = 7.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
14
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
15
Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
16
В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) докажите, что биссектриса угла С делит отрезок МN пополам
б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
17
Найдите все значения параметра a, при каждом из которых система уравнений
имеет ровно два различных решения.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
18
Дано трёхзначное натуральное число (число не может начинаться с нуля), не кратное 100.
а) Может ли частное этого числа и суммы его цифр быть равным 90?
б) Может ли частное этого числа и суммы его цифр быть равным 88?
в) Какое наибольшее натуральное значение может иметь частное данного числа и суммы его цифр?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Новый тренировочный вариант №41054170 ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
Скачать вариант, скачать ответы
Решу ЕГЭ 2022 по математике профильный уровень тренировочный вариант №41054170
Ответы для заданий ЕГЭ 2022
Задание 2 № 509412 У Вити в копилке лежит 12 рублёвых, 6 двухрублёвых, 4 пятирублёвых и 3 десятирублёвых монеты. Витя наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 70 рублей.
Ответ: 0,72
Задание 8 № 99597 Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Ответ: 25
Задание 10 № 320187 При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем— 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Ответ: 5
Задание 13 № 517563 Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник ABC с прямым углом C. Грань ACC1A1 является квадратом. а) Докажите, что прямые CA1 и AB1 перпендикулярны. б) Найдите расстояние между прямыми CA1 и AB1 , если AC = 4, BC = 7.
Задание 15 № 506958 Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.
Ответ: 18
Задание 16 № 505501 В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9. а) докажите, что биссектриса угла С делит отрезок МN пополам б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Ответ: 3:1
Задание 18 № 502027 Дано трёхзначное натуральное число (число не может начинаться с нуля), не кратное 100. а) Может ли частное этого числа и суммы его цифр быть равным 90? б) Может ли частное этого числа и суммы его цифр быть равным 88? в) Какое наибольшее натуральное значение может иметь частное данного числа и суммы его цифр?
Ответ: а) да; б) нет; в) 91.
Другие тренировочные варианты ЕГЭ по математике 11 класс:
Тренировочный вариант №144 ЕГЭ 2022 по математике 11 класс профильный уровень с ответами
28.09.2021 Математика 11 класс МА2110101-МА2110112 ЕГЭ 2022 работа статград ответы и задания
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Перейти к содержанию
На чтение 1 мин Просмотров 1 Опубликовано 5 марта, 2023
Решу ЕГЭ 2022 тренировочный вариант №41054170 по математике профильный уровень 11 класс с ответами Решение и ответы на задачи на официальном сайте источника онлайн.
Новый тренировочный вариант №41054170 ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии
Варианты ответов и решение задачи ТУТ: https://100ballnik.com/%d1%80%d0%b5%d1%88%d1%83-%d0%b5%d0%b3%d1%8d-2022-%d1%82%d1%80%d0%b5%d0%bd%d0%b8%d1%80%d0%be%d0%b2%d0%be%d1%87%d0%bd%d1%8b%d0%b9-%d0%b2%d0%b0%d1%80%d0%b8%d0%b0%d0%bd%d1%82-%e2%84%9641054170-%d0%bf/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
- ЕГЭ по математике профиль
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2022 из различных источников.
Тренировочные варианты ЕГЭ 2022 по математике (профиль)
Структура варианта КИМ ЕГЭ
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Связанные страницы:
Информация о генераторе вариантов:

Источники заданий:
1) Прототипы из fipi.ru;
2) Прототипы из os.fipi.ru;
3) Прототипы с реальных ЕГЭ всех лет;
4) Прототипы с mathege.ru.
На каждую позицию рандомно выпадает случайное задание из базы заданий.
Описание каждой из позиций №1–18:



• Задание 4. Вычисления и преобразования – на данный момент 10 прототипов.
• Задание 5. Стереометрия – на данный момент 10 прототипов.





Условия прототипов заданий первой части взяты у Евгения Пифагора из его видеокурса: «1–11 задания ЕГЭ профиль (первая часть с нуля)».
• Задание 12. Уравнения – на данный момент 10 прототипов.
• Задание 13. Стереометрическая задача – на данный момент 4 прототипа.
• Задание 14. Неравенства – на данный момент 10 прототипов.
• Задание 15. Финансовая математика – на данный момент 9 прототипов.
• Задание 16. Планиметрическая задача – на данный момент 4 прототипа.
• Задание 17. Задача с параметром – на данный момент 7 прототипов.
• Задание 18. Числа и их свойства – на данный момент 9 прототипов.


Примеры заданий, развёрнутая часть.

Время выполнения варианта.



Итог работы, ссылки на подробные решения всех задач.
Теги: тренировочные варианты, 11 класс, 2021, с ответами, новый вариант, профиль, пробный егэ.
Решу ЕГЭ
Автор 100balnik
ПОДЕЛИТЬСЯ
Новые тренировочные варианты в формате решу ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки к экзамену, каждый вариант составлен по новой демоверсии ФИПИ ЕГЭ 2022 года, к тренировочным заданиям прилагаются правильные ответы и пояснения.
-
Тренировочный вариант №41054170 с ответами
-
Тренировочный вариант №41054171 с ответами
-
Тренировочный вариант №41054172 с ответами
-
Тренировочный вариант №41054173 с ответами
-
Тренировочный вариант №41054174 с ответами
-
Тренировочный вариант №41054175 с ответами
-
Тренировочный вариант №41054176 с ответами
-
Тренировочный вариант №41054177 с ответами
-
Тренировочный вариант №41054178 с ответами
-
Тренировочный вариант №41054179 с ответами
-
Тренировочный вариант №41054180 с ответами
-
Тренировочный вариант №41054181 с ответами
-
Тренировочный вариант №41054182 с ответами
-
Тренировочный вариант №41054183 с ответами
-
Тренировочный вариант №41054184 с ответами
Другие тренировочные варианты ЕГЭ 2022 по математике:
Тренировочные варианты ЕГЭ по математике 11 класс задания с ответами
Пробный вариант ЕГЭ 2022 №211004 по математике 11 класс с ответами
1 августа 2021
В закладки
Обсудить
Жалоба
Утверждённые демоверсии ЕГЭ 2022 по математике от ФИПИ.
Обновлено 10 ноября.
→ Демоверсия профильного уровня: math-demo2022-pro-v2.pdf
→ Демоверсия базового уровня: math-demo2022-b-v2.pdf
→ Спецификация профильного уровня: math-s2022-pro-v2.pdf
→ Спецификация базового уровня: math-s2022-b-v2.pdf
→ Кодификатор: math-k2022-v2.pdf
→ Скачать одним архивом: math-demo2022-v2.zip
Изменения в КИМ ЕГЭ 2022 года профильного уровня в сравнении с КИМ 2021 года
1. Исключены задания 1 и 2, проверяющие умение использовать приобретённые знания и умения в практической и повседневной жизни, задание 3, проверяющее умение выполнять действия с геометрическими фигурами, координатами и векторами.
2. Добавлены задание 9, проверяющее умение выполнять действия с функциями, и задание 10, проверяющее умение моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий.
3. Внесено изменение в систему оценивания: максимальный балл за выполнение задания повышенного уровня 13, проверяющего умение выполнять действия с геометрическими фигурами, координатами и векторами, стал равен 3; максимальный балл за выполнение задания повышенного уровня 15, проверяющего умение использовать приобретённые знания и умения в практической деятельности и повседневной жизни, стал равен 2.
4. Количество заданий уменьшилось с 19 до 18, максимальный балл за выполнение всей работы стал равным 31.
Изменения в КИМ ЕГЭ 2022 года базового уровня в сравнении с КИМ 2021 года
1. Исключено задание 2, проверяющее умение выполнять вычисления и преобразования (данное требование внесено в позицию задачи 7 в новой нумерации).
2. Добавлены задание 5, проверяющее умение выполнять действия с геометрическими фигурами, и задание 20, проверяющее умение строить и исследовать простейшие математические модели.
3. Количество заданий увеличилось с 20 до 21, максимальный балл за выполнение всей работы стал равным 21.
Обобщенные планы вариантов КИМ ЕГЭ 2022 года по математике
Шкала перевода баллов по математике и другим предметам →
Тест «Витамины»
Проверочная работа по биологии в 8 классе.
Консультация по физике
Онлайн-трансляция по вопросам подготовки к ЕГЭ по физике.
Новое ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.admin2022-04-20T16:15:59+03:00
Варианты реальных и пробных ЕГЭ прошлых лет
Варианты профильного ЕГЭ
Тренировочные варианты ЕГЭ Профиль СтатГрад
Расписание СтатГрад ЕГЭ 2022
Демо вариант ЕГЭ Профиль 2022
Шкала перевода баллов ЕГЭ Профиль 2022
Методика определения минимального количества баллов ЕГЭ
1. Простейшие уравнения
Рациональные уравнения
Иррациональные уравнения
Показательные уравнения
Логарифмические уравнения
Тригонометрические уравнения
2. Начала теории вероятностей
Классическое определение вероятности
Теоремы о вероятностях событий
3. Планиметрия
Прямоугольный треугольник
Равнобедренный треугольник
Треугольник общего вида
Квадрат, прямоугольник, параллелограмм, ромб
Трапеция
Центральные и вписанные углы
Окружность, касательная, хорда, секущая
Вписанные окружности
Описанные окружности
4. Вычисления и преобразования
Вычисление значений рациональных выражений
Вычисление значений иррациональных выражений
Вычисление значений степенных выражений
Вычисление значений логарифмических выражений
Вычисление значений тригонометрических выражений
5. Стереометрия
Куб, прямоугольный параллелепипед
Элементы составных многогранников
Площадь поверхности и объем составного многогранника
Призма
Пирамида
Цилиндр, конус, шар
Комбинация тел
6. Производная и первообразная
Физический смысл производной
Геометрический смысл производной, касательная
Применение производной к исследованию функций
Первообразная
7. Задачи с прикладным содержанием
Рациональные уравнения и неравенства
Иррациональные уравнения и неравенства
Показательные и логарифмические уравнения и неравенства
Тригонометрические уравнения и неравенства
Разное
8. Текстовые задачи
Задачи на движение по прямой
Задачи на движение по окружности
Задачи на движение по воде
Задачи на работу
Задачи на проценты
Задачи на прогрессии
9. Анализ графиков
Прямая
Парабола
Гипербола
Логарифмическая и показательная функции
Иррациональные функции
Тригонометрические функции
10. Теория вероятностей повышенной сложности
Теоремы о вероятностях событий
Теория вероятностей повышенной сложности
11. Наибольшее и наименьшее значение функций
Степенные, иррациональные и дробные функции
Логарифмические функции
Показательные функции
Тригонометрические функции
Исследование функций без помощи производной
12. Уравнения
Рациональные уравнения
Уравнения с модулями
Иррациональные уравнения
Тригонометрические уравнения
Показательные уравнения
Логарифмические уравнения
Тригонометрические уравнения, содержащие ОДЗ
Уравнения смешанного типа, содержащие тригонометрические функции
13. Стереометрия
Вычисление отношений отрезков
Расстояние от точки до прямой. Расстояние от точки до плоскости
Угол между прямыми
Площадь сечения
Расстояние между скрещивающимися прямыми
Угол между плоскостями
Угол между прямой и плоскостью
Фигуры вращения: цилиндр, конус, шар
Объем многогранника
14. Неравенства
Рациональные неравенства
Неравенства с модулями
Показательные неравенства
Логарифмические неравенства
Логарифмические неравенства с переменным основанием
15. Финансовая математика
Задачи о вкладах и кредитовании
Экономические задачи на оптимизацию
16. Планиметрия
Треугольник и его элементы
Четырехугольники
Отношение отрезков и площадей
Окружности
Окружности, связанные с треугольником
Окружности, связанные с четырехугольником
17. Задача с параметром
Линейные уравнения, неравенства и системы уравнений с параметрами
Исследование дискриминанта и применение теоремы виета
Расположение корней квадратного трехчлена относительно данных чисел
Квадратные неравенства с параметрами
Задачи, сводящиеся к исследованию квадратного трехчлена
Применение монотонности и ограниченности функций к решению уравнений и неравенств
Применение инвариантности функций к решению уравнений и систем уравнений
Графический метод: преобразование и построение графиков в системе oxy
Графический метод: метод областей
Уравнения, неравенства и системы с параметрами
18. Числа и их свойства
Числа и их свойства
Числовые наборы на карточках и числах
Последовательности и прогрессии
Сюжетные задачи: кино, театр
Комментарии для сайта Cackle
ЕГЭ–2023, математика базовый уровень: задания, ответы, …
Web Материалы для подготовки к итоговому сочинению 2022–2023. 31 октября. Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР …
From mathb-ege.sdamgia.ru
ЕГЭ–2023, математика: задания, ответы, решения
Web i. При двух одновременно работающих принтерах расход бумаги составляет 1 пачку за 12 минут. Определите, за сколько минут израсходует пачку бумаги первый …
From math-ege.sdamgia.ru
ЕГЭ–2023, математика базовый уровень: задания, ответы, …
Web 22 декабря. Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам! 4 ноября. Материалы для подготовки к итоговому сочинению …
From mathb-ege.sdamgia.ru
Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс …
Web Пробный ЕГЭ 2023 профиль по математике вариант 25 вариант_25_егэ2023_профиль_математика Ответы и решения …
From 100ballnik.com
ЕГЭ–2023: задания, ответы, решения — SDAMGIA
Web Профильный уровень. … Материалы для подготовки к итоговому сочинению 2022–2023. 31 октября. Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, …
From ege.sdamgia.ru
ЕГЭ–2023, математика: задания, ответы, решения
Web 4 ноября. Материалы для подготовки к итоговому сочинению 2022–2023. 31 октября. Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР. 21 марта. Новый …
From math-ege.sdamgia.ru
Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс …
Web Тренировочный вариант №26 пробник решу ЕГЭ 2023 по математике 11 класс профильный уровень от 8 марта 2023 года с ответами и решением по новой …
From 100ballnik.com
Решу ЕГЭ 2022 тренировочный вариант №41054175 по …
Web Решу ЕГЭ 2022 по математике профильный уровень тренировочный вариант №41054175 Ответы и решения для варианта: Задание 2 № 282856 При …
From 100ballnik.com
Решу ЕГЭ 2022 тренировочный вариант №41054179 по …
Web Решу ЕГЭ 2022 по математике профильный уровень тренировочный вариант №41054179 Ответы и решения для варианта: Задание 2 № 320191 На олимпиаде …
From 100ballnik.com
Решу ЕГЭ 2022 тренировочный вариант №41054171 по …
Web Решу ЕГЭ 2022 по математике профильный уровень тренировочный вариант №41054171 Ответы и решения для варианта: Задание 2 № 500037 Проводится …
From 100ballnik.com
Решу ЕГЭ 2022 тренировочный вариант №41054172 по …
Web Решу ЕГЭ 2022 по математике профильный уровень тренировочный вариант №41054172 Ответы и решения для варианта: Задание 2 № 320186 На рок …
From 100ballnik.com
ЕГЭ–2023, математика: задания, ответы, решения
Web В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр …
From math-ege.sdamgia.ru
Решу ЕГЭ 2022 тренировочный вариант №41054170 по …
Web Решу ЕГЭ 2022 по математике профильный уровень тренировочный вариант №41054170 Ответы для заданий ЕГЭ 2022 Задание 2 № 509412 У Вити в копилке …
From 100ballnik.com
ЕГЭ–2023: задания, ответы, решения — SDAMGIA
Web Для тех, кто ищет варианты посложнее, чем обычно предлагают на ЕГЭ, публикуем задания с развернутым ответом из тренировочных вариантов А. А. Ларина. Новые …
From math-ege.sdamgia.ru
ЕГЭ–2023, английский язык: задания, ответы, решения
Web Профильный уровень. … Материалы для подготовки к итоговому сочинению 2022–2023. 31 октября. Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР …
From en-ege.sdamgia.ru
ЕГЭ–2023, русский язык: задания, ответы, решения
Web Базовый уровень. Профильный уровень … Материалы для подготовки к итоговому сочинению 2022–2023. 31 октября. Сертификаты для учителей о работе на Решу …
From rus-ege.sdamgia.ru
ЕГЭ–2023, английский язык: задания, ответы, решения
Web 1. Тип 41 № 10723. Task 3. You are going to give an interview. You have to answer five questions. Give full answers to the questions (2−3 sentences). Remember that you have …
From en-ege.sdamgia.ru
Задание 4 решу ЕГЭ 2022 математика профильный уровень 100 …
Web Более 100 тренировочных прототипов задания №4 решу ЕГЭ 2022 по математике 11 класс профильный уровень с ответами и решением для практики. Задание №4 …
From 100ballnik.com
ЕГЭ–2023, информатика: задания, ответы, решения
Web Более подробные аналитические и методические материалы ЕГЭ 2021 года доступны по ссылке. На нашем сайте представлены около 3200 заданий для подготовки к …
From inf-ege.sdamgia.ru
ЕГЭ–2023, математика базовый уровень: задания, ответы, …
Web Единицы измерений писать не нужно. Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. …
From mathb-ege.sdamgia.ru
ЕГЭ–2023, математика базовый уровень: задания, ответы, …
Web i. Ананасы стоят 85 руб. за штуку. Какое максимальное число ананасов можно купить на 500 руб., если их цена снизится на 20%? Ответ: 2. Тип 2 № 507050. i. …
From mathb-ege.sdamgia.ru
ЕГЭ–2023: задания, ответы, решения
Web Базовый уровень. Профильный уровень … Материалы для подготовки к итоговому сочинению 2022–2023. 31 октября. Сертификаты для учителей о работе на Решу …
From ege.sdamgia.ru
Тренировочный вариант №26 решу ОГЭ 2023 по математике 9 …
Web Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 …
From 100ballnik.com
ЕГЭ–2023: задания, ответы, решения — SDAMGIA
Web Для подготовки к перечневым олимпиадам! 4 ноября. Материалы для подготовки к итоговому сочинению 2022–2023. 31 октября. Сертификаты для учителей о работе …
From ege.sdamgia.ru
Вариант 41054170 егэ математика
Новый тренировочный вариант №41054170 ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
Решу ЕГЭ 2022 по математике профильный уровень тренировочный вариант №41054170
Ответы для заданий ЕГЭ 2022
Задание 2 № 509412 У Вити в копилке лежит 12 рублёвых, 6 двухрублёвых, 4 пятирублёвых и 3 десятирублёвых монеты. Витя наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 70 рублей.
Ответ: 0,72
Задание 8 № 99597 Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Ответ: 25
Задание 10 № 320187 При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем— 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Ответ: 5
Задание 13 № 517563 Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник ABC с прямым углом C. Грань ACC1A1 является квадратом. а) Докажите, что прямые CA1 и AB1 перпендикулярны. б) Найдите расстояние между прямыми CA1 и AB1 , если AC = 4, BC = 7.
Задание 15 № 506958 Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.
Ответ: 18
Задание 16 № 505501 В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9. а) докажите, что биссектриса угла С делит отрезок МN пополам б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Ответ: 3:1
Задание 18 № 502027 Дано трёхзначное натуральное число (число не может начинаться с нуля), не кратное 100. а) Может ли частное этого числа и суммы его цифр быть равным 90? б) Может ли частное этого числа и суммы его цифр быть равным 88? в) Какое наибольшее натуральное значение может иметь частное данного числа и суммы его цифр?
Решу ЕГЭ 2022 тренировочный вариант №41054170 по математике профильный уровень 11 класс с ответами
Новый тренировочный вариант №41054170 ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
Задание 2 № 509412 У Вити в копилке лежит 12 рублёвых, 6 двухрублёвых, 4 пятирублёвых и 3 десятирублёвых монеты. Витя наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 70 рублей.
Ответ: 0,72
Задание 8 № 99597 Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Ответ: 25
Задание 10 № 320187 При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем— 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Ответ: 5
Задание 13 № 517563 Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник ABC с прямым углом C. Грань ACC1A1 является квадратом. а) Докажите, что прямые CA1 и AB1 перпендикулярны. б) Найдите расстояние между прямыми CA1 и AB1 , если AC = 4, BC = 7.
Задание 15 № 506958 Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.
Ответ: 18
Задание 16 № 505501 В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9. а) докажите, что биссектриса угла С делит отрезок МN пополам б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Ответ: 3:1
Задание 18 № 502027 Дано трёхзначное натуральное число (число не может начинаться с нуля), не кратное 100. а) Может ли частное этого числа и суммы его цифр быть равным 90? б) Может ли частное этого числа и суммы его цифр быть равным 88? в) Какое наибольшее натуральное значение может иметь частное данного числа и суммы его цифр?
А Докажите, что прямые CA1 и AB1 перпендикулярны.
100ballnik. com
10.04.2019 16:38:12
2019-04-10 16:38:12
Источники:
Https://100ballnik. com/%D1%80%D0%B5%D1%88%D1%83-%D0%B5%D0%B3%D1%8D-2022-%D1%82%D1%80%D0%B5%D0%BD%D0%B8%D1%80%D0%BE%D0%B2%D0%BE%D1%87%D0%BD%D1%8B%D0%B9-%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82-%E2%84%9641054170-%D0%BF/
Решу ЕГЭ 2022 тренировочный вариант №41054171 по математике профильный уровень 11 класс с ответами | ЕГЭ ОГЭ СТАТГРАД ВПР 100 баллов » /> » /> .keyword { color: red; } Вариант 41054170 егэ математика
Решу ЕГЭ 2022 тренировочный вариант №41054171 по математике профильный уровень 11 класс с ответами
Решу ЕГЭ 2022 тренировочный вариант №41054171 по математике профильный уровень 11 класс с ответами
Новый тренировочный вариант №41054171 ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
Решу ЕГЭ 2022 по математике профильный уровень тренировочный вариант №41054171
Ответы и решения для варианта:
Задание 2 № 500037 Проводится жеребьёвка Лиги Чемпионов. На первом этапе жеребьёвки восемь команд, среди которых команда «Барселона», распределились случайным образом по восьми игровым группам— по одной команде в группу. Затем по этим же группам случайным образом распределяются еще восемь команд, среди которых команда «Зенит». Найдите вероятность того, что команды «Барселона» и «Зенит» окажутся в одной игровой группе.
Ответ: 0,125
Задание 10 № 319353 Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая— 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая— 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Ответ: 0,019
Задание 13 № 509502 В кубе ABCDA1B1C1D1 все рёбра равны 4. На его ребре BB1 отмечена точка K так, что KB = 3. Через точкиK и C1 построена плоскость α, параллельная прямой BD1 . а) Докажите, что A1P : PB1 = 2 : 1, где P — точка пересечения плоскости α с ребром A1B1 . б) Найдите угол наклона плоскости α к плоскости грани BB1C1C.
Задание 15 № 520787 15-го декабря планируется взять кредит в банке на 1 000 000 рублей на ( n + 1) месяц. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца; — cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца с 1-го по n — й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца; — 15-го числа n-го месяца долг составит 200 тысяч рублей; — к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен. Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1378 тысяч рублей.
Ответ: 3
Задание 16 № 505425 Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H. а) Докажите, что ∠ AHB1 = ∠ACB. б) Найдите BC, если AH = 4 и ∠BAC = 60°.
Решу ЕГЭ 2022 тренировочный вариант №41054171 по математике профильный уровень 11 класс с ответами
Новый тренировочный вариант №41054171 ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки, данный вариант составлен по новой демоверсии ФИПИ экзамена ЕГЭ 2022 года, к тренировочным заданиям прилагаются решения и правильные ответы.
Задание 2 № 500037 Проводится жеребьёвка Лиги Чемпионов. На первом этапе жеребьёвки восемь команд, среди которых команда «Барселона», распределились случайным образом по восьми игровым группам— по одной команде в группу. Затем по этим же группам случайным образом распределяются еще восемь команд, среди которых команда «Зенит». Найдите вероятность того, что команды «Барселона» и «Зенит» окажутся в одной игровой группе.
Ответ: 0,125
Задание 10 № 319353 Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая— 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая— 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Ответ: 0,019
Задание 13 № 509502 В кубе ABCDA1B1C1D1 все рёбра равны 4. На его ребре BB1 отмечена точка K так, что KB = 3. Через точкиK и C1 построена плоскость α, параллельная прямой BD1 . а) Докажите, что A1P : PB1 = 2 : 1, где P — точка пересечения плоскости α с ребром A1B1 . б) Найдите угол наклона плоскости α к плоскости грани BB1C1C.
Задание 15 № 520787 15-го декабря планируется взять кредит в банке на 1 000 000 рублей на ( n + 1) месяц. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца; — cо 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца с 1-го по n — й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца; — 15-го числа n-го месяца долг составит 200 тысяч рублей; — к 15-му числу (n + 1)-го месяца кредит должен быть полностью погашен. Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1378 тысяч рублей.
Ответ: 3
Задание 16 № 505425 Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H. а) Докажите, что ∠ AHB1 = ∠ACB. б) Найдите BC, если AH = 4 и ∠BAC = 60°.
Решу ЕГЭ 2022 по математике профильный уровень тренировочный вариант 41054171.
100ballnik. com
06.07.2017 13:06:52
2017-07-06 13:06:52
Источники:
Https://100ballnik. com/%D1%80%D0%B5%D1%88%D1%83-%D0%B5%D0%B3%D1%8D-2022-%D1%82%D1%80%D0%B5%D0%BD%D0%B8%D1%80%D0%BE%D0%B2%D0%BE%D1%87%D0%BD%D1%8B%D0%B9-%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82-%E2%84%9641054171-%D0%BF/
Вариант 41054170 егэ математика » /> » /> .keyword { color: red; } Вариант 41054170 егэ математика
Вариант 41054170 егэ математика
Вариант 41054170 егэ математика
Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.
Решение. Последовательно получаем:
Значениям соответствуют положительные корни.
Значениям соответствуют меньшие значения корней.
Следовательно, наибольшим отрицательным корнем является число
У Вити в копилке лежит 12 рублёвых, 6 двухрублёвых, 4 пятирублёвых и 3 десятирублёвых монеты. Витя наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 70 рублей.
Решение. У Вити в копилке лежит 12 + 6 + 4 + 3 = 25 монет на сумму 12 + 12 + 20 + 30 = 74 рубля. Больше 70 рублей останется, если достать из копилки либо рублёвую, либо двухрублёвую монету. Таких монет 12 + 6 = 18. Искомая вероятность равна 18 : 25 = 0,72.
В треугольнике ABC угол C равен 90°, CH − высота, Найдите
Решение. Имеем:
Найдите если при
Решение. Выполним преобразования:
Объем параллелепипеда равен 4,5. Найдите объем треугольной пирамиды
Решение. Искомый объем равен разности объемов параллелепипеда и четырех пирамид, основания которых являются гранями данной треугольной пирамиды. Объём каждой из этих пирамид равен одной трети произведения площади основания на высоту, а площадь основания вдвое меньше площади основания параллелепипеда:
На рисунке изображен график функции Y = F(X). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите
Решение. Поскольку касательная проходит через начало координат, её уравнение имеет вид Y = kx. Эта прямая проходит через точку (8; 10), поэтому 10 = 8 · K, откуда K = 1,25. Поскольку угловой коэффициент касательной равен значению производной в точке касания, получаем:
При температуре рельс имеет длину м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону где — коэффициент теплового расширения, — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.
Решение. Задача сводится к решению уравнения мм при заданных значениях длины м и коэффициента теплового расширения :
Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.
Решение. Пусть км/ч — скорость третьего велосипедиста, а T ч — время, которое понадобилось ему, чтобы догнать второго велосипедиста. Таким образом,
А через 2 часа 20 минут после этого догнал первого. Таким образом,
Если взять за x скорость третьего велосипедиста, можно составить уравнение: 10/(x − 10) + 8/3 =30/(x − 15). Принимая во внимание, что x больше 15, получаем ответ 25.
На рисунке изображён график функции вида где числа A, B, C и D — целые. Найдите
Решение. По графику тогда и
По графику тогда, если то
— не имеет целочисленных решений,
Найдём наименьший положительный период функции
Наименьший положительный период функции равен а по графику наименьший положительный период равен 2, тогда
Таким образом, Найдём
При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
В ответе укажите наименьшее необходимое количество выстрелов.
Решение. Найдем вероятность противоположного события, состоящего в том, что цель не будет уничтожена за N выстрелов. Вероятность промахнуться при первом выстреле равна 1 − 0,4 = 0,6, а при каждом следующем 1 − 0,6 = 0,4. Эти события независимые, вероятность их произведения равна произведению вероятности этих событий. Поэтому вероятность промахнуться при N выстрелах равна:
Осталось найти наименьшее натуральное решение неравенства
Последовательно проверяя значения N, равные 1, 2, 3 и т. д. находим, что искомым решением является Следовательно, необходимо сделать 5 выстрелов.
Можно решать задачу «по действиям», вычисляя вероятность уцелеть после ряда последовательных промахов:
Р(2) = Р(1)·0,4 = 0,24.
Р(3) = Р(2)·0,4 = 0,096.
Р(4) = Р(3)·0,4 = 0,0384;
Р(5) = Р(4)·0,4 = 0,01536.
Последняя вероятность меньше 0,02, поэтому достаточно пяти выстрелов по мишени.
Приведем другое решение.
Вероятность поразить мишень равна сумме вероятностей поразить ее при первом, втором, третьем и т. д. выстрелах. Поэтому задача сводится к нахождению наименьшего натурального решения неравенства
В нашем случае неравенство решается подбором, в общем случае понадобится формула суммы геометрической прогрессии, использование которой сведет задачу к простейшему логарифмическому неравенству.
Найдите наименьшее значение функции на отрезке
Решение. Найдем производную заданной функции:
Найдем нули производной:
Отметим на рисунке нули производной и поведение функции на заданном отрезке:
Следовательно, наименьшим значением функции на заданном отрезке является ее значение в точке минимума. Найдем его:
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение. а) Преобразуем уравнение:
Б) Ограничим каждое полученное решение из пункта «а» и решим эти неравенства:
Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник ABC с прямым углом C. Грань ACC1A1 является квадратом.
А) Докажите, что прямые CA1 и AB1 перпендикулярны.
Б) Найдите расстояние между прямыми CA1 и AB1, если AC = 4, BC = 7.
Решение. а) Заметим, что B1 C1 ⊥ C1 A1 как катеты прямоугольного треугольника, и B1 C1 ⊥ C1 C, поскольку призма прямая. Тогда по признаку перпендикулярности прямой и плоскости Кроме того, как диагонали квадрата. AB1 − наклонная, AC1 − ее проекция на плоскость ACA1, − прямая в плоскости перпендикулярная проекции. Тогда по теореме о трёх перпендикулярах что и требовалось доказать.
Б) Пусть M − середина AC1. Тогда искомое расстояние равно расстоянию от точки M до прямой AB1, поскольку прямая A1C перпендикулярна плоскости AB1C1. Это расстояние равно половине высоты прямоугольного треугольника AB1C1, проведённой к гипотенузе, то есть
При обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Решение. Решим неравенство:
Чтобы не решать кубическое неравенство, можно подобрать подходящую группировку:
Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.
Решение. Пусть сумма кредита S у. е., процентная ставка банка X %.
Предложение «Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину» означает: Антон взятую сумму возвращал в банк равными долями. Сумма, образованная применением процентной ставки, составляет:
Общая сумма, выплаченная Антоном за 6 месяцев: (у. е.). А эта сумма по условию задачи равна у. е. Решим уравнение:
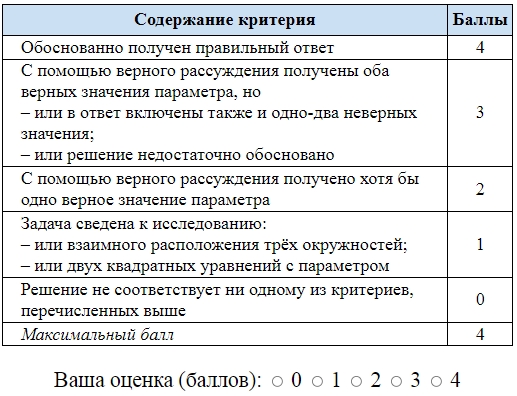
Критерии оценивания выполнения заданияБаллы
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
А) докажите, что биссектриса угла С делит отрезок МN пополам
Б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Решение. а) Обозначим K точку пересечения отрезков AM и BN. Треугольник ABN равнобедренный, так как в нем AK является биссектрисой и высотой. Следовательно, AK является и медианой, то есть K — середина BN. Получаем, что AN = AB = 6, откуда NC = AC − AN = 3.
Рассмотрим треугольник ABC, биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам: BM : MC = AB : AC, учитывая, что длина BC равна 5, получаем: BM = 2; MC = 3.
В треугольнике MNC стороны NC и MC равны, следовательно, треугольник MNC — равнобедренный, с основанием MN. Значит, биссектриса угла C также является медианой и высотой. Таким образом, получаем, что биссектриса угла С делит отрезок MN пополам.
Б) Рассмотрим треугольник PMN: отрезок PO перпендикулярен прямой MN и делит её пополам, следовательно, треугольник PMN — равнобедренный с основанием MN. Значит, PM = PN и отношение AP : PN = AP : PM.
В треугольнике AMC отрезок CP — биссектриса, поэтому AP : PM = AC : MC = 3 : 1.
При обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
При какой температуре рельс удлинится на 3 мм.
Ege. sdamgia. ru
20.06.2020 20:32:45
2020-06-20 20:32:45
Источники:
Https://ege. sdamgia. ru/test? id=41054170&print=true
Реальные варианты ЕГЭ по математике
Дорогие друзья! На этой странице вы можете найти варианты реальных КИМ ЕГЭ по математике (база и профиль). На сайте размещены только ссылки на варианты КИМ ЕГЭ и их решения. Здесь вы можете сказать тренировочный и реальный вариант ЕГЭ по математике (профиль и база) 2022 и 2023 гг с ответами и решениями. Если материалы вам пригодились, можете финансово поддержать работу сайта через форму ниже:
2022-2023 учебный год
| Реальный вариант ЕГЭ по математике-2023 | ||
| Скачать вариант (профиль) | Решение и ответы | 02.06.2023 |
| Досрочные варианты ЕГЭ по математике-2023 | ||
| Скачать вариант 1 (профиль) | Решение и ответы | 28.03.2023 |
| Открытый вариант досрочного ЕГЭ по математике-2023 | ||
| Скачать вариант (профиль) |
Решение и ответы | 28.03.2023 |
| Скачать вариант (база) | Решение и ответы | 28.03.2023 |
| Демонстрационный вариант ЕГЭ по математике-2023 | ||
| Вариант (профиль) | Спецификация | Кодификатор |
| Вариант (база) | Спецификация | |
| Тренировочные работы Статград в формате ЕГЭ по математике-2023 | ||
| Тренировочная работа №1
Профиль База |
Ответы и решения | 28 сентября 2021 г. |
| Тренировочная работа №2
Профиль База |
Ответы и решения | 15 декабря 2021 г. |
| Тренировочная работа №3
Профиль База |
Ответы и решения (профиль) | 27 января 2022 г. |
| Тренировочная работа №4
Профиль База |
||
| Тренировочная работа №5
Профиль База |
Ответы и решения | 28 апреля 2022 г. |
2021-2022 учебный год
| Реальный вариант ЕГЭ по математике-2022 | ||
| Скачать вариант (профиль) Дальний Восток | Решение и ответы | 02.06.2022 |
| Досрочные варианты ЕГЭ по математике-2022 | ||
| Скачать вариант 1 (профиль) | Решение и ответы | 28.03.2022 |
| Скачать вариант 2 (профиль) | Решение и ответы | 28.03.2022 |
| Скачать вариант 3 (профиль) | Решение и ответы | 28.03.2022 |
| Скачать вариант 4 (профиль) | Решение и ответы | 28.03.2022 |
| Открытый вариант досрочного ЕГЭ по математике-2022 | ||
| Скачать вариант (профиль) |
Решение и ответы | 28.03.2022 |
| Скачать вариант (база) | Решение и ответы | 28.03.2022 |
| Демонстрационный вариант ЕГЭ по математике-2022 | ||
| Вариант (профиль) | Спецификация | Кодификатор |
| Вариант (база) | Спецификация | |
| Перспективный вариант демо-версии КИМ ЕГЭ по математике-2022 |
||
| Вариант | Спецификация | |
| Тренировочные работы Статград в формате ЕГЭ по математике-2022 | ||
| Тренировочная работа №1 (профиль)
Тренировочная работа №1 (база) |
Ответы и решения | 28 сентября 2021 г. |
| Тренировочная работа №2 (профиль) Варианты 1 и 2Варианты 3 и 4 |
Ответы и решения | 15 декабря 2021 г. |
| Тренировочная работа №3 (профиль)
Тренировочная работа №3 (база) |
Ответы и решения (профиль) | 27 января 2022 г. |
| Тренировочная работа №4 | ||
| Тренировочная работа №5 (база)
Тренировочная работа №5, варианты 1 и 2 (профиль) Тренировочная работа №5, варианты 3 и 4 (профиль) |
Ответы и решения | 28 апреля 2022 г. |
2020-2021 учебный год
| Реальные варианты КИМ ЕГЭ по математике | ||
| Основная волна ЕГЭ по математике-2021 | ||
| Вариант 1 | Ответы и решения | |
| Открытый вариант ЕГЭ по математике-2021 от ФИПИ | ||
| Вариант (профиль) | Ответы и решения | |
| Демонстрационный вариант ЕГЭ по математике-2021 (проект) | ||
| Вариант Ответы | Кодификатор | Спецификация |
|
Тренировочные варианты ЕГЭ по математике-2021 |
||
| Вариант 1
Вариант 2 |
Вариант 1 — ответы и решения
Вариант 2 — ответы, критерии |
Admin
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.