Скрыть
3 января 2031 года на вкладе будет сумма на 5 января 2030 года, увеличенная на 5%: $$Scdot 1,05=24,15to S=23$$ млн. Т.к. вклад на 5% увеличивается равномерно, то каждый год будет в сумме расти на $$frac{23-3}{2030-2020}=2$$ млн.
2020: № года: — ; вклад 2 января: — ; добавил на вклад 4 января: — ; вклад 5-го января: 3
2021: № года: 1; вклад 2 января: $$3+0,1cdot 3$$; добавил на вклад 4 января: $$5-3,3=1,7$$; вклад 5-го января: $$5$$
2022: № года: 2; вклад 2 января: $$5+0,1cdot 5$$; добавил на вклад 4 января: $$7-5,5=1,5$$; вклад 5-го января: $$7$$
2023: № года: 3; вклад 2 января: $$7+0,1cdot 7$$; добавил на вклад 4 января: $$9-7,7=1,3$$; вклад 5-го января: $$9$$
2024: № года: 4; вклад 2 января: $$9+0,05cdot 9$$; добавил на вклад 4 января: $$1,55$$; вклад 5-го января: $$11$$
2025: № года: 5; вклад 2 января: $$11+0,05cdot 11$$; добавил на вклад 4 января: $$1,45$$; вклад 5-го января: $$13$$
2026: № года: 6; вклад 2 января: $$13+0,05cdot 13$$; добавил на вклад 4 января: $$1,35$$; вклад 5-го января: $$15$$
$$dots $$
2030: № года: 10; вклад 2 января: $$21+0,05cdot 21$$; добавил на вклад 4 января: $$0,95$$; вклад 5-го января: $$23$$
2031: № года: 11; вклад 2 января: $$23+0,05cdot 23=24,15$$;
Начисления банка составят: $$0,1left(3+5+7right)+0,05(9+11+13+15+17+19+21+23)=$$ $$=0,1cdot 15+0,05cdot frac{9+23}{2}cdot 8=1,5+6,4=7,9 $$млн. руб.
Решение и ответы заданий № 1–12 варианта №325 Александра Ларина. Разбор ЕГЭ 2021 по математике (профильный уровень).
Задание 1.
В 14‐этажном доме расположены 336 квартир по 4 квартиры на этаже. Между этажами по два лестничных пролета, по 11 ступенек каждый. Лифты сломались, а старший по дому обходит квартиры в порядке возрастания номеров (начиная с первой). Прохождение каждых 50 ступенек обходится ему появлением новой мозоли. Сколько мозолей он заработал за вечер, обойдя 170 квартир и выйдя из дома (ступеньки для входа на первый этаж не считаются)?
(Автор задачи Николай Журавлев)
Задание 2.
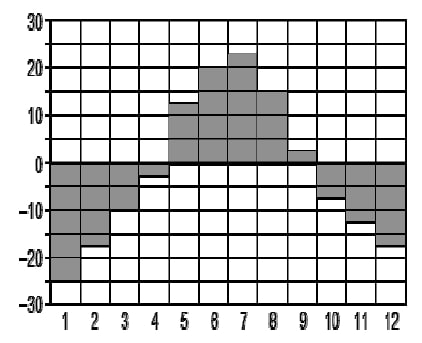
На диаграмме показана среднемесячная температура воздуха в Новосибирске за каждый месяц 1892 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме, какой была средняя температура (в градусах Цельсия) в самом прохладном летнем месяце.
Задание 3.
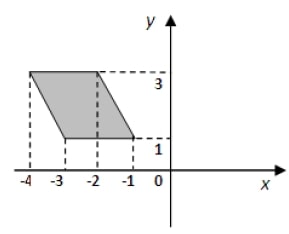
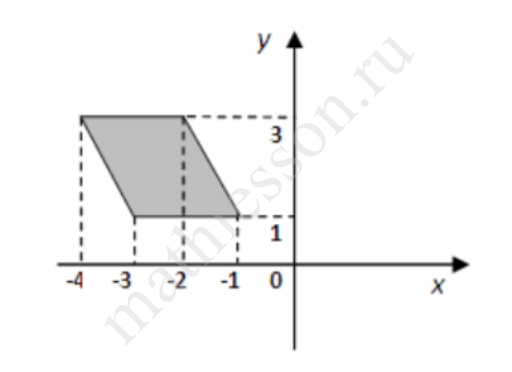
Найдите площадь закрашенного четырехугольника.
Задание 4.
При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем – 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Задание 5.
Решите уравнение (х + 3)2 = (х + 3)4. В ответе укажите меньший корень.
Задание 6.
Равнобокая трапеция АВСD разбивается диагональю АС на два равнобедренных треугольника. Определите, чему равен больший угол трапеции. Ответ дайте в градусах.
Задание 7.
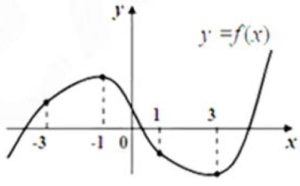
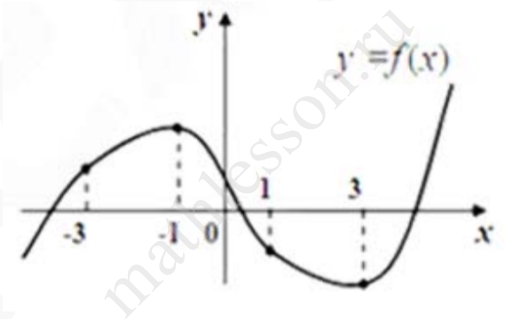
На графике функции у = f (x) отмечены четыре точки с абсциссами ‐3, ‐1, 1, 3. По данному графику определите, в какой из этих точек значение производной f ′(x) будет наибольшим. (В ответе укажите абсциссу этой точки).
Задание 8.
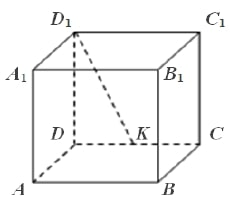
Ребро куба равно ABCDA1B1C1D1 равно 2√5. Точка К – середина ребра СD. Найдите расстояние между прямыми АD и D1К.
Задание 9.
Найдите значение выражения
Задание 10.
По закону Ома для полной цепи сила тока, измеряемая в амперах, равна , где ε – ЭДС источника (в вольтах), r = 2,4 Ом – его внутреннее сопротивление, R – сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 24% от силы тока короткого замыкания Iк.з. =
? (Ответ выразите в омах).
Задание 11.
Первые 4 дня на строительстве объекта трудились 13 рабочих, после чего к ним присоединились еще трое, а спустя 3 дня шестеро рабочих были переведены на другой объект. За какой срок (в днях) будет построен данный объект, если шесть рабочих могут выполнить это задание за 20 дней?
Задание 12.
Найдите наименьшее значение функции f(x) = 5 – log2(31 – x2 – 2x)
Источник варианта: alexlarin.net
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
А. Ларин. Тренировочный вариант № 325. (часть C).
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
Дан прямой круговой конус с вершиной М. Осевое сечение конуса — треугольник с углом 120° при вершине М. Образующая конуса равна Через точку М проведено сечение конуса, перпендикулярное одной из образующих.
а) Докажите, что получившийся в сечении треугольник — тупоугольный.
б) Найдите расстояние от центра О основания конуса до плоскости сечения.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
Решите неравенство:
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В остроугольном треугольнике АВС провели высоты АН1 и СН2, затем провели луч НМ, который пересекает окружность, описанную около треугольника АВС, в точке К, где М — середина АС, а Н — точка пересечения высот.
а) Докажите, что НМ = МК.
б) Найдите площадь треугольника ВСК, если
AC = 1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
5 января 2020 года Андрей планирует открыть вклад на сумму 3 миллиона рублей. Первые три года 2 января банк будет начислять 10% на сумму вклада, а в последующие годы банк будет начислять 5% на сумму вклада.
4 января каждого года Андрей будет делать дополнительный взнос на вклад так, чтобы после этого величина вклада на 5 января была больше величины вклада на 5 января прошлого года на одно и то же число. Определите общий размер начислений банка, если 3 января 2031 года на вкладе будет лежать 24,15 миллиона рублей.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
Найдите все значения параметра a, при каждом из которых система уравнений
имеет ровно 1 решение.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
Назовем натуральное число «замечательным», если оно самое маленькое среди натуральных чисел с такой же, как у него, суммой цифр.
а) Чему равна сумма цифр две тысячи пятнадцатого замечательного числа?
б) Сколько существует двухзначных замечательных чисел?
в) Какой порядковый номер замечательного числа 5999?
г) Чему равна сумма всех четырехзначных замечательных чисел?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
325 вариант егэ математика профиль 2022
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
А. Ларин. Тренировочный вариант № 325. (часть C).
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие промежутку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Дан прямой круговой конус с вершиной М. Осевое сечение конуса — треугольник с углом 120° при вершине М. Образующая конуса равна Через точку М проведено сечение конуса, перпендикулярное одной из образующих.
А) Докажите, что получившийся в сечении треугольник — тупоугольный.
Б) Найдите расстояние от центра О основания конуса до плоскости сечения.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
—>
325 вариант егэ математика профиль 2022.
Ege. sdamgia. ru
06.01.2018 0:37:55
2018-01-06 00:37:55
Источники:
Https://ege. sdamgia. ru/test? id=34559207
Вариант №325 ЕГЭ Ларин » /> » /> .keyword { color: red; } 325 вариант егэ математика профиль 2022
Вариант №325 ЕГЭ Ларин
Вариант №325 ЕГЭ Ларин
Решение и ответы заданий № 1–12 варианта №325 Александра Ларина. Разбор ЕГЭ 2021 по математике (профильный уровень).
Задание 1.
В 14‐этажном доме расположены 336 квартир по 4 квартиры на этаже. Между этажами по два лестничных пролета, по 11 ступенек каждый. Лифты сломались, а старший по дому обходит квартиры в порядке возрастания номеров (начиная с первой). Прохождение каждых 50 ступенек обходится ему появлением новой мозоли. Сколько мозолей он заработал за вечер, обойдя 170 квартир и выйдя из дома (ступеньки для входа на первый этаж не считаются)?
(Автор задачи Николай Журавлев)
Задание 2.
На диаграмме показана среднемесячная температура воздуха в Новосибирске за каждый месяц 1892 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме, какой была средняя температура (в градусах Цельсия) в самом прохладном летнем месяце.
Задание 3.
Найдите площадь закрашенного четырехугольника.
Задание 4.
При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем – 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Задание 5.
Решите уравнение (х + 3) 2 = (х + 3) 4 . В ответе укажите меньший корень.
Задание 6.
Равнобокая трапеция АВСD разбивается диагональю АС на два равнобедренных треугольника. Определите, чему равен больший угол трапеции. Ответ дайте в градусах.
Задание 7.
На графике функции у = f (x) отмечены четыре точки с абсциссами ‐3, ‐1, 1, 3. По данному графику определите, в какой из этих точек значение производной f ′(x) будет наибольшим. (В ответе укажите абсциссу этой точки).
Задание 8.
Ребро куба равно ABCDA1B1C1D1 равно 2√5. Точка К – середина ребра СD. Найдите расстояние между прямыми АD и D1К.
Задание 9.
Найдите значение выражения
Задание 10.
По закону Ома для полной цепи сила тока, измеряемая в амперах, равна, где ε – ЭДС источника (в вольтах), r = 2,4 Ом – его внутреннее сопротивление, R – сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 24% от силы тока короткого замыкания Iк. з. = ? (Ответ выразите в омах).
Задание 11.
Первые 4 дня на строительстве объекта трудились 13 рабочих, после чего к ним присоединились еще трое, а спустя 3 дня шестеро рабочих были переведены на другой объект. За какой срок (в днях) будет построен данный объект, если шесть рабочих могут выполнить это задание за 20 дней?
Задание 12.
Найдите наименьшее значение функции f(x) = 5 – log2(31 – x 2 – 2x)
Найдите значение выражения
За какой срок в днях будет построен данный объект, если шесть рабочих могут выполнить это задание за 20 дней.
Ege314.ru
21.12.2020 8:03:48
2020-12-21 08:03:48
Источники:
Вариант 325 Ларина, решение ЕГЭ математика 2021 | Виктор Осипов » /> » /> .keyword { color: red; } 325 вариант егэ математика профиль 2022
325 вариант Алекса Ларина. Разбор ЕГЭ математика 2021
325 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.

В 14-этажном доме расположены 336 квартир по 4 квартиры на этаже. Между этажами по два лестничных пролета, по 11 ступенек каждый. Лифты сломались, а старший по дому обходит квартиры в порядке возрастания номеров (начиная с первой). Прохождение каждых 50 ступенек обходится ему появлением новой мозоли. Сколько мозолей он заработал за вечер, обойдя 170 квартир и выйдя из дома (ступеньки для входа на первый этаж не считаются)?

Скрыть $$frac=42,5$$ этажей вверх надо пройти $$to frac=3frac$$ подъезда. Т. е. 3 раза он поднимется на 14 этаж и спустится обратно. Количество пролетов в 3-х подъездах: $$2cdot 13cdot 3=78$$ пролетов $$to 78cdot 11=858$$ ступенек, т. е. $$858cdot 2=1716$$ ступенек пройдет. Оставшиеся квартиры на первом этаже 4-го подъезда, их несчитаем. Тогда $$frac=34,32to $$ 34 мозоли.
Задание 2
На диаграмме показана среднемесячная температура воздуха в Новосибирске за каждый месяц 1892 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, какой была средняя температура (в градусах Цельсия) в самом прохладном летнем месяце.

Задание 3
Найдите площадь закрашенного четырехугольника.

Скрыть Дан параллелограмм: $$S=ah=left(-1-left(-3right)right)cdot left(3-1right)=2cdot 2=4$$.
Задание 4
При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?

Скрыть Вероятность не уничтожения цели тогда менее $$left(1-0,98right)=0,02.$$ Промах при первом выстреле: $$1-0,4=0,6.$$ Далее $$1-0,6=0,4.$$ Тогда через n выстрелов вероятность не уничтожения:
Задание 5
Решите уравнение $$<left(x+3right)>^2=<left(x+3right)>^4$$. В ответе укажите меньший корень.

Задание 6
Равнобокая трапеция АВСD разбивается диагональю АС на два равнобедренных треугольника. Определите, чему равен больший угол трапеции. Ответ дайте в градусах.

Скрыть $$triangle ABC$$ — равнобедренный, $$AB=BCto angle BAC=angle BCA=alpha ;$$ $$angle BCA=angle CAD=alpha $$ (накрест лежащие при $$BCparallel AD$$). Тогда $$angle A=2alpha =angle D.$$ Но из $$triangle ACD: angle ADC=frac^circ -alpha >.$$ Тогда:
$$2alpha =frac^circ -alpha >to 4alpha =180<>^circ -alpha to alpha =36<>^circ to angle B=180-2cdot 36=108<>^circ $$
Задание 7
На графике функции $$у = f (x)$$ отмечены четыре точки с абсциссами $$-3, -1, 1, 3.$$ По данному графику определите, в какой из этих точек значение производной $$f'(x)$$ будет наибольшим. (В ответе укажите абсциссу этой точки).

Скрыть $$f’left(xright)=$$, где $$alpha$$ — угол м/у $$Ox$$ и касательной. При этом при $$alpha to 90<>^circ left(alpha Аналоги к этому заданию:
Задание 8
Ребро куба $$ABCDA_1B_1C_1D_1$$ равно $$2sqrt$$. Точка $$К$$ — середина ребра $$CD$$. Найдите расстояние между прямыми $$AD$$ и $$D_1K.$$

Скрыть Пусть DH — высота $$triangle DD_1K.$$ Т. к. $$ADbot left(DCC_1right),$$ то $$ADbot DHto DH$$ — общий перпендикуляр. $$DK=fracDC=sqrtto $$ из
Задание 9
Найдите значение выражения $$<<log >_2 sqrt-1> >+<<log >_4 (1+sqrt) >$$

Задание 10
По закону Ома для полной цепи сила тока, измеряемая в амперах, равна $$I=frac$$, где $$varepsilon $$ — ЭДС источника (в вольтах), $$r=2,4$$ Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 24% от силы тока короткого замыкания $$I_1=frac$$? (Ответ выразите в омах).

Задание 11
Первые 4 дня на строительстве объекта трудились 13 рабочих, после чего к ним присоединились еще трое, а спустя 3 дня шестеро рабочих были переведены на другой объект. За какой срок (в днях) будет построен данный объект, если шесть рабочих могут выполнить это задание за 20 дней?

Скрыть Производительность одного рабочего $$x$$ объектов в сутки, тогда $$6xcdot 20=1to x=frac.$$ Пусть $$y$$ дней после перевода шестерых. Тогда: $$13xcdot 4+16xcdot 3+10xcdot y=1to 100x+10xy=1to$$$$ frac+frac=1to y=2.$$ Тогда весь срок: $$4+3+2=9$$ дней.
Задание 12
Найдите наименьшее значение функции $$fleft(xright)=5-<<log >_2 (31-x^2-2x) >$$

Скрыть Пусть $$gleft(xright)=31-x^2-2xto fleft(xright)to min,$$ если $$<<log >_2 (31-x^2-2x) >to max$$ или $$gleft(xright)to max.$$ Наибольшее будет в вершине параболы: $$x_0=-frac=-1to gleft(-1right)=31-1+2=32to$$$$ fleft(-1right)=5-<<log >_2 32 >=0$$
Задание 13
Б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac<pi >;2pi ]$$

Задание 14
Дан прямой круговой конус с вершиной М. Осевое сечение конуса — треугольник с углом $$120<>^circ $$ при вершине М. Образующая конуса равна $$2sqrt$$. Через точку М проведено сечение конуса, перпендикулярное одной из образующих.
А) Докажите, что получившийся в сечении треугольник — тупоугольный
Б) Найдите расстояние от центра О основания конуса до плоскости сечения.
Задание 15

$$(1): left(1-6x-1+2x-x^2right)left(-xright)>0leftrightarrow left(-x^2-4xright)left(-xright)>0leftrightarrow x^2left(x+4right)>0leftrightarrow $$ $$leftrightarrow x>-4.$$ Тогда: $$xin (-4;0)cup (0;frac)$$.
Задание 16
В остроугольном треугольнике АВС провели высоты $$AH_1$$ и $$CH_2$$, затем провели луч МН, который пересекает описанную около треугольника АВС в точке К, где М — середина АС, а Н — точка пересечения высот.
А) Докажите, что $$НМ=МК$$
Б) Найдите площадь треугольника ВСК, если $$angle ABC=60<>^circ ; angle BAC=45<>^circ ; AC=1$$
Задание 17
5-го января 2020-го года Андрей планирует положить на депозит вклад размером 3 миллиона рублей. Первые три года 2-го января банк начисляет 10% на сумму вклада, а в последующие годы банк начисляет 5% на сумму вклада.
4-го января каждого года Андрей делает дополнительный взнос на вклад так, чтобы после этого величина вклада на 5 января была больше величины вклада на 5 января прошлого года на одно и то же число. Определить общий размер начислений банка, если 3-го января 2031-го года на вкладе будет лежать 24,15 миллиона рублей.

3 января 2031 года на вкладе будет сумма на 5 января 2030 года, увеличенная на 5%: $$Scdot 1,05=24,15to S=23$$ млн. Т. к. вклад на 5% увеличивается равномерно, то каждый год будет в сумме расти на $$frac=2$$ млн.
2020: № года: — ; вклад 2 января: — ; добавил на вклад 4 января: — ; вклад 5-го января: 3
2021: № года: 1; вклад 2 января: $$3+0,1cdot 3$$; добавил на вклад 4 января: $$5-3,3=1,7$$; вклад 5-го января: $$5$$
2022: № года: 2; вклад 2 января: $$5+0,1cdot 5$$; добавил на вклад 4 января: $$7-5,5=1,5$$; вклад 5-го января: $$7$$
2023: № года: 3; вклад 2 января: $$7+0,1cdot 7$$; добавил на вклад 4 января: $$9-7,7=1,3$$; вклад 5-го января: $$9$$
2024: № года: 4; вклад 2 января: $$9+0,05cdot 9$$; добавил на вклад 4 января: $$1,55$$; вклад 5-го января: $$11$$
2025: № года: 5; вклад 2 января: $$11+0,05cdot 11$$; добавил на вклад 4 января: $$1,45$$; вклад 5-го января: $$13$$
2026: № года: 6; вклад 2 января: $$13+0,05cdot 13$$; добавил на вклад 4 января: $$1,35$$; вклад 5-го января: $$15$$
2030: № года: 10; вклад 2 января: $$21+0,05cdot 21$$; добавил на вклад 4 января: $$0,95$$; вклад 5-го января: $$23$$
2031: № года: 11; вклад 2 января: $$23+0,05cdot 23=24,15$$;
Начисления банка составят: $$0,1left(3+5+7right)+0,05(9+11+13+15+17+19+21+23)=$$ $$=0,1cdot 15+0,05cdot fraccdot 8=1,5+6,4=7,9 $$млн. руб.
По закону Ома для полной цепи сила тока, измеряемая в амперах, равна $I=frac$, где $varepsilon $ — ЭДС источника (в вольтах), $r=2,4$ Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 24% от силы тока короткого замыкания $I_1=frac$? (Ответ выразите в омах).

Первые 4 дня на строительстве объекта трудились 13 рабочих, после чего к ним присоединились еще трое, а спустя 3 дня шестеро рабочих были переведены на другой объект. За какой срок (в днях) будет построен данный объект, если шесть рабочих могут выполнить это задание за 20 дней?

Скрыть Производительность одного рабочего $x$ объектов в сутки, тогда $6xcdot 20=1to x=frac.$ Пусть $y$ дней после перевода шестерых. Тогда: $13xcdot 4+16xcdot 3+10xcdot y=1to 100x+10xy=1to$$ frac+frac=1to y=2.$ Тогда весь срок: $4+3+2=9$ дней.
Тогда через n выстрелов вероятность не уничтожения.
Mathlesson. ru
22.03.2018 11:58:21
2018-03-22 11:58:21
Источники:
Https://mathlesson. ru/larin325var-ege
На чтение 1 мин Просмотров 1 Опубликовано 5 марта, 2023
Вариант №325 ЕГЭ Ларин Решение и ответы на задачи на официальном сайте источника онлайн.
Решение и ответы заданий № 1–12 варианта №325 Александра Ларина. Разбор ЕГЭ 2021 по математике (профильный уровень).
Варианты ответов и решение задачи ТУТ: https://ege314.ru/ege-varianty-larina/variant-325-ege-larin/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
Тренировочные варианты №325 Алекса Ларина пробный ОГЭ 2022 по математике 9 класс с ответами и решением по новой демоверсии сайта ФИПИ ОГЭ 2022 года для подготовки к экзамену, дата выхода варианта на сайте: 11.05.2022 (11 мая 2022 года)
Скачать тренировочный вариант Ларина №325
Скачать усложненную версию варианта
Вариант Ларина №325 ОГЭ 2022 по математике 9 класс задания и ответы
огэ2022_ларин_математика_вариант325
Настя летом отдыхает у дедушки в деревне Александровке. В воскресенье они собираются съездить на машине в село Фомино. Из Александровки в Фомино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе — через деревню Новомальцево до деревни Парахино, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Фомино. Есть и третий маршрут: в Новомальцева можно свернуть на прямую грунтовую дорогу, которая идёт мимо озера прямо в Фомино. По шоссе Настя с дедушкой едут со скоростью 60 км/ч, а по грунтовой дороге — 50 км/ч. На плане изображено взаимное расположение населённых пунктов, сторона каждой клетки равна 3 км.
1)Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов, запятых и других разделительных символов.
Ответ: 3421
2)Найдите расстояние от деревни Александровки до села Фомино по прямой. Ответ выразите в километрах.
Ответ: 45
3)Сколько километров проедут Настя с дедушкой, если они поедут по шоссе через Парахино?
Ответ: 63
4)Сколько времени затратят на дорогу Настя с дедушкой, если они поедут сначала до Новомальцево, а затем свернут на грунтовую дорогу, идущую мимо озера? Ответ выразите в минутах.
Ответ: 58,8
5)Определите, на какой маршрут потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Настя с дедушкой, если поедут этим маршрутом.
Ответ: 54
10)В каждой пятидесятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Наташа покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Наташа не найдёт приз в своей банке.
Ответ: 0,98
14)При свободном падении тело прошло в первую секунду 5 м, а в каждую следующую на 10 м больше. Найдите глубину шахты (в метрах), если свободно падающее тело достигло его дна через 5 с после начала падения.
Ответ: 125
17)Найдите тангенс угла AOB , изображённого на рисунке.
Ответ: 2
19)Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов. 1) Центром окружности, вписанной в правильный треугольник, является точка пересечения медиан. 2) В любой правильный многоугольник можно вписать не менее одной окружности. 3) Центр окружности, вписанной в тупоугольный треугольник, находится вне этого треугольника. 4) В любой треугольник можно вписать не менее одной окружности.
Ответ: 124
Смотрите также на нашем сайте:
Статград математика 9 класс ОГЭ 2022 пробные варианты с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
| Автор | Сообщение | |||||||
|---|---|---|---|---|---|---|---|---|
|
Заголовок сообщения: Re: Тренировочный вариант №325
|
||||||||
|
Всем здравствуйте! Решение заданий 13 и 15. Подробности: Решение задания 17. Подробности: Решение задания 18. Подробности:
|
|||||||
  |
||||||||
|
|
||||||||
|
netka |
Заголовок сообщения: Re: Тренировочный вариант №325
|
|||||||
|
Решение задания 14. Вложение:
скрин решения Подробности: |
|||||||
  |
||||||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №325
|
|||||||
|
Решение задачи 18 Подробности:
|
|||||||
  |
||||||||
|
khazh |
Заголовок сообщения: Re: Тренировочный вариант №325
|
|||||||
|
№14 Подробности: №16 Подробности: №18 Подробности: |
|||||||
  |
||||||||
|
Raisa |
Заголовок сообщения: Re: Тренировочный вариант №325
|
|||||||
|
Решение задач 11, 13. Подробности:
|
|||||||
  |
||||||||
|
Raisa |
Заголовок сообщения: Re: Тренировочный вариант №325
|
|||||||
|
Решение задач 15, 16. Подробности:
|
|||||||
  |
||||||||
| Показать сообщения за: Сортировать по: |
Кто сейчас на форуме
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
|
Вы не можете начинать темы |
|
|