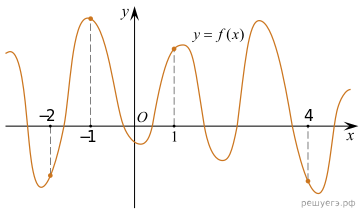
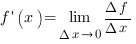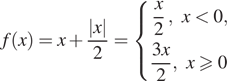На рисунке изображен график функции и отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Спрятать решение
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Производная отрицательна в точках −1 и 4. Модуль тангенса угла наклона касательной явно больше в точке 4, поэтому тангенс в этой точке наименьший.
Ответ:4.
Источник: Досрочный ЕГЭ по математике (Центр) 30.03.2018
04
Фев 2013
06 Задание (2022)ПРОИЗВОДНАЯ
Задачи на производную и касательную
В этом году в Задании 7 из Открытого банка заданий для подготовки к ЕГЭ по математике появились новые задачи. Давайте разберем их решение.
Прототип задания B8 (№ 317543)
На рисунке изображен график функции y=f(x) и отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Как мы знаем, производной называется
предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
Производная в точке показывает скорость изменения функции в данной точке. Чем быстрее изменяется функция, то есть чем больше приращение функции, тем больше угол наклона касательной. Поскольку в задаче требуется определить точку, в которой значение производной наибольшее, исключим из рассмотрения точки с абсциссами -1 и 1 — в этих точках функция убывает, и производная в них отрицательна.
Функция возрастает в точках -2 и 2. Однако, возрастает она в них по-разному — в точке -2 график функции поднимается круче, чем в точке 2, и следовательно, приращение функции в этой точки, а, значит и производная — больше.
Ответ: -2
И аналогичная задача:
Прототип задания B8 (№ 317544)
На рисунке изображен график функции и отмечены точки -2, -1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Решение этой задачи аналогично решению предыдущей «с точностью до наоборот»
Нас интересует точка, в которой производная принимает наименьшее значение, то есть мы ищем точку, в которой функция уменьшается наиболее быстро — на графике это точка, в которой самый крутой «спуск». Это точка с абсциссой 4.
Ответ: 4.
И.В. Фельдман, репетитор по математике.

Исследование функции на возрастание и убывание по графикам с
помощью производной.
Краткая
теория
На
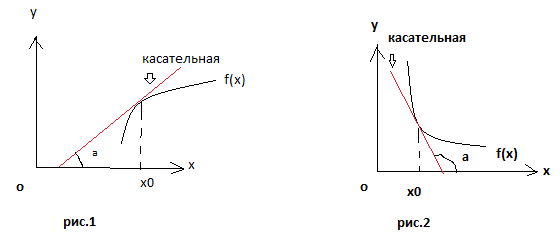
рис.1 угол наклона касательной с положительным направлением оси ОХ – острый, а
на рис.2 этот угол тупой. Если угол
наклона касательной острый, это означает, что производная
в этой точке положительна,
и функция при увеличении значения переменной Х будет возрастать.( см. рис.1). Если угол наклона касательной тупой, как на рис.2, это означает, что производная в это точке отрицательна, и функция на этом участке убывает. (см.рис. 2.). Итак, условие
возрастания и убывания функции:
еслиf ´(x) > 0 на некотором
промежутке, то функция возрастает на этом промежутке, если f ´(x)< 0 на некотором
промежутке, то функция убывает на этом промежутке,
У
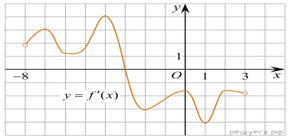
функции может быть несколько участков убывания и возрастания. Рис. 3.Разберем пример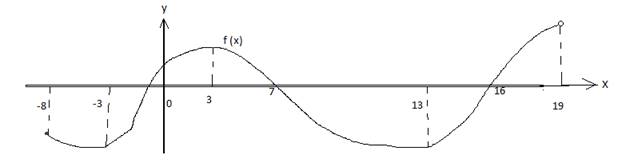
график некоторой функции f (x). Функция возрастает
на промежутках [-3;3] и [13;19]. На этих промежутках угол наклона касательной
с положительным направлением оси ОХ острый, значит производная f ´(x) > 0, так как тангенс
острого угла положителен. Функция убывает на промежутках [ -8; -3] и
[3;13], так как на этих участках угол наклона касательной с положительным
направлением оси ОХ тупой, значит производная f ´(x) < 0, так как тангенс
тупого угла отрицательный. Если надо определить
участки возрастания и убывания не по графику, а путем вычислений, то действуют
по такому
плану:
1. Найти область определения заданной
функции.
2. Найти производную f
´(x)
заданной функции.
3. Найти промежутки, где производная f ´(x) > 0 и f ´(x) < 0, ( решая полученные
неравенства аналитически или методом интервалов).
Пример1. Исследовать функцию f(x) = 5x2 -3x +1на монотонность
(на возрастание и убывание). Решение.
- Область
определения функцииD(f) = R. - f
´(x) = (5x2 -3x +1)´ = 10x – 3 - f ´(x) = 0 10x -3 =0 10x=3 x= 0,3
Отметим найденную точку на числовой прямой. Числовая
прямая разбилась на два промежутка (-∞; 0,3] и [0,3; + ∞).Проверим
знак производной в каждом из полученных промежутков. Для этого выбираем любое
произвольное число из левого промежутка и потом из правого. Выберем любое
число х<0,3, например х=0 и подставим вместо х в производную, получим:
10·0 -3= -3< 0.Поставим слева от числа 0,3 знак минус на числовой прямой.
Выберем любое число х>0,3, например, х=2 и
подставим вместо х в производную, получим: 10·2 -3= 17>0.Поставим справа
от числа 0,3 знак плюс на числовой прямой. Там, где производная положительна (f ´(x) >0) функция возрастает, то есть возрастает на промежутке [
0,3; +∞)
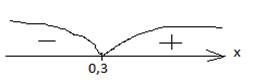
отрицательна
(f ´(x)<0) функция
убывает, то есть убывает на ( -∞; 0,3].
Пример2. Исследовать функцию f(x) = 3x2 –2x3+12х на возрстание и
убывание. Найти длину участка возрастания.
1.Область
определения функции D(f) = R.
2. f ´(x) = (3x2 -2x3 +12х)´= 6х
– 6х2 +12
3. f ´(x) = 0 6х – 6х2
+12 =0 разделим на 6 и перепишем по порядку. — х2 +х +2 = 0
Решим это квадратное уравнение, найдем дискриминант и корни.
D= 12 —
4·(-1)·2 = 1 + 8 = 9>0 — два корня.
X1= ( — 1+√9)/
( -2) =2/ (-2)= — 1; X2= ( — 1-√9)/ ( -2) =2
Отметим
найденные точки на числовой прямой. Числовая прямая разбилась на три
промежутка:
(-∞;
-1] , [-1; 2] и [2; +∞). Проверим знак производной в каждом промежутке.
На (-∞; -1] выберем, например, х = -3 и подставим в производную. . f ´(-3)= — (
-3)2 +(-3) +2= -9 -3 +2 = -10<0
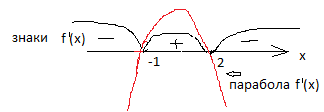
В
случае, когда производная получилась в виде квадратичной функции, то знак в
каждом промежутке проверять не надо, достаточно определить знак в одном
промежутке, в остальных знаки будут обязательно чередоваться, или как на рисунке
изобразить схематически график квадратичной функции (
красный график).
Изобразим
числовую прямую и расставим знаки производной.
Производная
положительна на [-1; 2] , значит на этом промежутке функция возрастает.
Производная отрицательна на промежутках (-∞; — 1] и [2; +∞),
значит функция убывает на этих промежутках. Найдем длину участка
возрастания 2 – (-1) = 2 +1 =3.
Ответ: функция
возрастает на промежутке[-1; 2] , убывает на промежутках
(-∞;
— 1] и [2; +∞). Длина участка возрастания равна 3.
Рассмотрим примеры на исследование функции на возрастание и
убывание по графикам.
1.
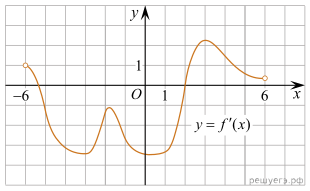
график производной функции определенной на
интервале Найдите
промежутки возрастания функции В ответе укажите сумму
целых точек, входящих в эти промежутки.
Решение. Промежутки возрастания
данной функции f(x) соответствуют промежуткам, на которых ее
производная неотрицательна, то есть промежуткам (−6; −5,2] и [2; 6).
Данные промежутки содержат целые точки 2, 3, 4 и 5. Их сумма равна 14.
Ответ: 14.
2.
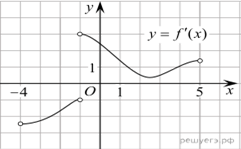
На рисунке изображён график —
производной функции определенной на
интервале (−8; 3). В какой точке отрезка [−3; 2]
функция принимает наибольшее
значение?
Решение. Функция,
дифференцируемая на отрезке [a; b], непрерывна на нем. Если
функция непрерывна на отрезке [a; b], а её производная
положительна (отрицательна) на интервале (a; b), то функция
возрастает (убывает) на отрезке [a; b].
На заданном отрезке производная функции не положительна, функция
на этом отрезке убывает. Следовательно, наибольшее значение функции достигается
на левой границе отрезка, т. е. в точке −3.
Ответ: −3.
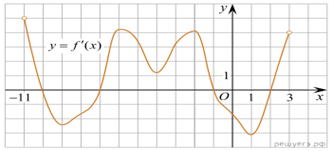
3.
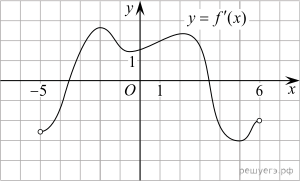
На рисунке изображен график производной функции f(x),
определенной на интервале (−11; 3). Найдите промежутки возрастания
функции f(x). В ответе укажите длину наибольшего из них.
Решение. Функция,
дифференцируемая на отрезке [a; b], непрерывна на нем. Если
функция непрерывна на отрезке [a; b], а её производная
положительна (отрицательна) на интервале (a; b), то функция
возрастает (убывает) на отрезке [a; b].
Поэтому промежутки возрастания функции f(x) соответствуют
промежуткам, на которых производная функции неотрицательна, то есть промежуткам
(−11; −10], [−7; −1] и [2; 3).
Наибольший из них — отрезок [−7; −1], длина
которого равна 6.
Ответ: 6.
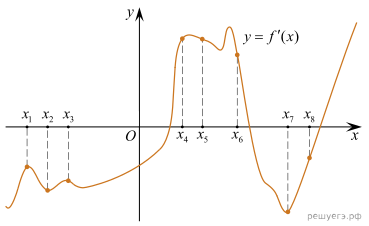
4. На рисунке изображён график —
производной функции f(x). На оси абсцисс отмечены восемь точек: x1,
x2, x3, …, x8. Сколько
из этих точек лежит на промежутках возрастания функции f(x)?
Решение. Возрастанию
дифференцируемой функции f(x) соответствуют неотрицательные
значения её производной. Производная неотрицательна в точках x4,
x5, x6. Таких точек 3 Ответ: 3.
5.
На рисунке изображен график функции и отмечены точки
−2, −1, 1, 4. В какой из этих точек значение производной
наименьшее? В ответе укажите эту точку.
Решение. Значение производной в
точке касания равно угловому коэффициенту касательной, который в свою очередь
равен тангенсу угла наклона данной касательной к оси абсцисс. Производная
отрицательна в точках −1 и 4. Модуль тангенса угла наклона касательной
явно больше в точке 4, поэтому тангенс в этой точке наименьший.
Ответ:4.
6.
На рисунке изображён график дифференцируемой функции y = f(x).
На оси абсцисс отмечены девять точек: x1, x2,
x3, …, x9. Среди этих точек найдите все
точки, в которых производная функции f(x) отрицательна. В ответе
укажите количество найденных точек.
Решение. 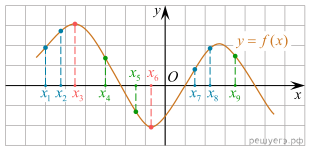
являются точками экстремума функции f(x). Это точки x3
и x6 (выделены красным). В них производная функции f(x)
равна нулю.
В точках x1, x2, x7
и x8 функция f(x) возрастает (выделены синим).
В этих четырёх точках производная функции f(x) положительна.
В точках x4, x5 и x9
функция f(x) убывает (выделены зеленым). В этих трёх
точках производная функции f(x) отрицательна.
Ответ: 3.
7.
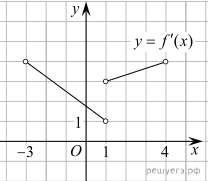
определена и непрерывна
на интервале На рисунке
изображен график её производной. Найдите промежутки возрастания функции В ответе укажите сумму
целых точек, входящих в эти промежутки.
Решение. Промежутки возрастания
данной функции f(x) соответствуют промежуткам, на которых её
производная неотрицательна, то есть интервалам (−3; 1) и
(1; 4). В силу непрерывности функция f(x) возрастает на
интервале (−3; 4). Данный промежуток содержит целые точки −2,
−1, 0, 1, 2 и 3. Их сумма равна 3.
Ответ: 3.
Примечание.
Напомним, что если функция непрерывна на каком-либо из концов
промежутка возрастания или убывания, то граничную точку присоединяют к этому
промежутку. В частности, если функция непрерывна на отрезке и монотонна на
интервале то функция монотонна
на всем отрезке
Обобщением этого утверждения служит следующая теорема: функция монотонна на промежутке,
если ее производная сохраняет знак всюду на этом промежутке, за исключением
конечного числа точек, в которых функция непрерывна. Например, производная
функции
не существует в точке и положительна
во всех остальных точках. Функция f в точке непрерывна,
следовательно, она возрастает на
8.
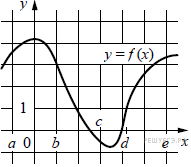
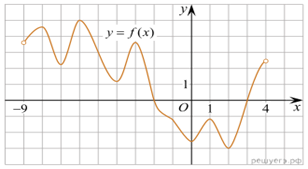
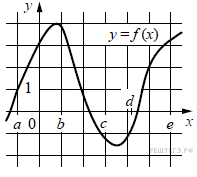
На рисунке изображён график функции y = f(x).
Числа a, b, c, d и e задают на оси x четыре интервала.
Пользуясь графиком, поставьте в cоответствие каждому интервалу характеристику
функции или её производной.
Ниже указаны значения производной в данных точках. Пользуясь
графиком, поставьте в соответствие каждой точке значение производной
в ней.
|
ТОЧКИ |
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
|
|
А) (a; b) Б) (b; c) В) (c; d) Г) (d; e) |
1) производная отрицательна на всём интервале 2) производная положительна в начале интервала и отрицательна 3) функция отрицательна в начале интервала и положительна 4) производная положительна на всём интервале |
Запишите в ответ цифры, расположив их в порядке, соответствующем
буквам:
Пояснение.
Если функция возрастает, то производная
положительна и наоборот.
На интервале (a;b)производная
положительна вначале интервала и отрицательна в конце, потому
что функция вначале возрастает, а потом убывает.
На интервале (b;c)
производная отрицательна, потому что функция убывает.
На интервале (c;d)
функция отрицательна в начале интервала и положительна в конце интервала.
На интервале (d;e)
производная положительна, потому что функция возрастает.
Таким образом, получаем соответствие
А — 2, Б — 1, В — 3 и Г — 4.
Ответ: 2134.
Решить самостоятельно.
1.
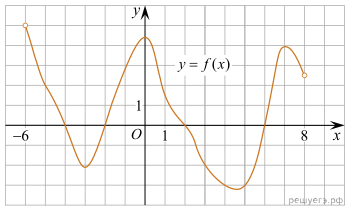
график функции y = f(x), определенной на интервале
(−6; 8). Определите количество целых точек, в которых производная функции
положительна.
2.
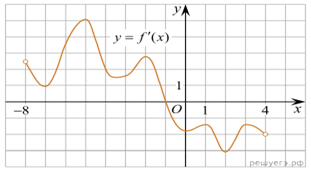
график производной функции f(x), определенной на интервале
(−8; 4). В какой точке отрезка [−7; −3] f(x)
принимает наименьшее значение?
3.
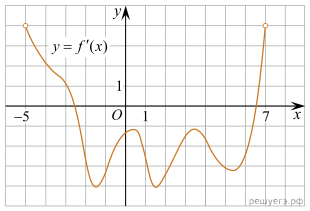
график производной функции f(x), определенной на интервале
(−5; 7). Найдите промежутки убывания функции f(x). В ответе
укажите сумму целых точек, входящих в эти промежутки.
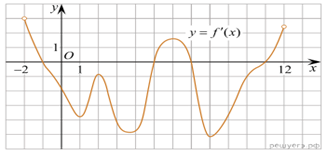
4.
На рисунке изображен график производной функции f(x),
определенной на интервале (−2; 12). Найдите промежутки убывания
функции f(x). В ответе укажите длину наибольшего из них.
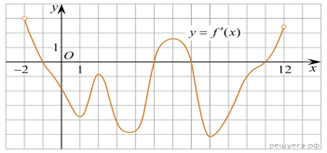
5.
На рисунке изображен график производной функции f(x),
определенной на интервале (−2; 12). Найдите промежутки убывания
функции f(x). В ответе укажите длину наибольшего из них.
6.
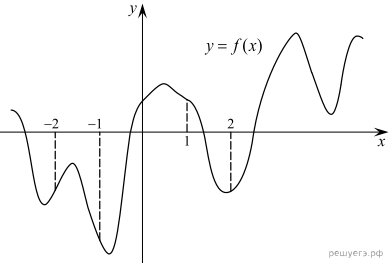
график функции и отмечены точки
−2, −1, 1, 2. В какой из этих точек значение производной
наибольшее? В ответе укажите эту точку.
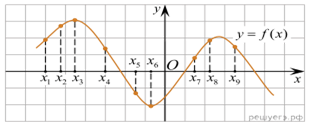
7.

график функции y = f(x) и отмечены семь
точек на оси абсцисс: x1, x2, x3,
x4, x5, x6, x7.
В скольких из этих точек производная функции f(x) отрицательна?
Решение. Производная функции
отрицательна в тех точках, которые принадлежат участкам убывания функции. Это
точки x3, x4, x7 —
всего 3 точки.
8.
На рисунке изображён график функции и восемь точек на оси
абсцисс: В скольких из этих точек
производная функции положительна?
9. На рисунке изображён график функции и двенадцать точек на
оси абсцисс: В скольких из этих точек
производная функции отрицательна?
10.
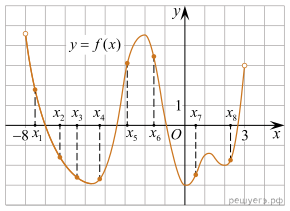
график функции определенной на
интервале . Сколько из
отмеченных точек принадлежат промежуткам
убывания функции?
11
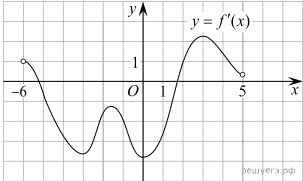
определена и непрерывна
на отрезке На рисунке
изображен график её производной. Найдите промежутки возрастания функции В ответе укажите сумму
целых точек, входящих в эти промежутки.
12.
Функция определена и непрерывна
на отрезке На рисунке
изображен график её производной. Найдите промежутки убывания функции В ответе укажите сумму
целых точек, входящих в эти промежутки.
13
Функция определена и непрерывна
на полуинтервале На рисунке
изображен график её производной. Найдите промежутки возрастания функции В ответе укажите сумму
целых точек, входящих в эти промежутки.
14.
На рисунке изображён график функции определённой на
интервале (−9; 4). Найдите промежутки убывания функции f(x).
В ответе укажите длину наибольшего из них.
15.
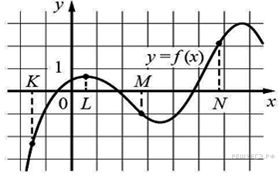
На рисунке
изображён график функции y = f(x) и отмечены точки K,
L, M и N на оси x. Пользуясь графиком, поставьте
в соответствие каждой точке характеристику функции и её производной.
Ниже указаны значения производной в данных точках. Пользуясь
графиком, поставьте в соответствие каждой точке значение производной
в ней.
|
ТОЧКИ |
ХАРАКТЕРИСТИКИ ФУНКЦИИ ИЛИ ПРОИЗВОДНОЙ |
|
|
А) K Б) L В) M Г) N |
1) функция положительна, производная положительна 2) функция отрицательна, производная отрицательна 3) функция положительна, производная равна 0 4) функция отрицательна, производная положительна |
В таблице под каждой буквой укажите соответствующий
номер.
16.
На рисунке изображён график функции y = f(x) .
Точки a, b, c, d и e задают на оси Ox
интервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу
характеристику функции или её производной.
Пользуясь графиком, поставьте в соответствие каждому интервалу
времени характеристику движения автомобиля на этом интервале.
|
ИНТЕРВАЛЫ ВРЕМЕНИ |
ХАРАКТЕРИСТИКИ |
|
|
А) (a; b) Б) (b; c) В) (c; d) Г) (d; e) |
1) Значения функции положительны в каждой точке 2) Значения производной функции положительны в каждой точке 3) Значения функции отрицательны в каждой точке 4) Значения производной функции отрицательны в каждой точке |
Запишите в ответ цифры, расположив их в порядке, соответствующем
буквам:
17. Исследовать
функцию f(x) = 5 +2x3— 24х на возрастание и убывание.
Найти длину участка убывания.
18. Исследовать функцию f(x) = x2 – x4 + 1 на возрстание и
убывание. Найти длину наименьшего участка возрастания.
Ответы
на задания.
1. 4
2. -7
3. 18
4. 6
5. 6
6. – 2
7. 3
8. 5
9. 7
10.
4
11.
8
12.
6
13.
9
14.
3
15.
4321
16.
1432
17.
↓ [-2; 2]; ↑ ( — ∞; -2] и [2; +∞). Длина участка ↓
равна 4.
18.
↓ [-1; 0] и [1; +∞); ↑ ( — ∞; -1] и [0; 1]. Длина наименьшего
участка ↑ равна 1.
Скачано с www.znanio.ru
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Новые тренировочные варианты ЕГЭ 2023 по математике базовый и профильный уровень с ответами и решением для 10 и 11 класса, больше 100 вариантов в формате реального экзамена ФИПИ вы можете решать онлайн или скачать.
Тренировочные варианты ЕГЭ 2023 по математике база и профиль
13.09.2022 Тренировочный вариант №1 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 по математике профиль с ответами
20.09.2022 Тренировочный вариант №2 ЕГЭ 2023 база по математике с ответами
27.09.2022 Математика 11 класс профиль входная мониторинговая работа 3 варианта с ответами
28.09.2022 Тренировочный вариант №3 ЕГЭ 2023 база по математике с ответами
28 сентября 2022 Статград математика 11 класс ЕГЭ 2023 база и профиль варианты и ответы
29 сентября 2022 Тренировочный вариант №3 ЕГЭ 2023 по математике профиль с ответами
1 октября 2022 Ларин вариант 399 ЕГЭ 2023 по математике профиль решение с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 база по математике с ответами
6 октября Тренировочный вариант №4 ЕГЭ 2023 по математике профиль с ответами
8 октября Ларин вариант 400 ЕГЭ 2023 по математике профиль решение с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 база по математике с ответами
12 октября Тренировочный вариант №5 ЕГЭ 2023 по математике профиль с ответами
14 октября Вариант 1 Ященко ЕГЭ 2023 математика профиль с ответами и решением
14 октября Вариант 2 Ященко ЕГЭ 2023 математика профиль с ответами и решением
15 октября Ларин вариант 401 ЕГЭ 2023 по математике профиль решение с ответами
15 октября Ларин вариант 402 ЕГЭ 2023 по математике профиль решение с ответами
16 октября Вариант 3 Ященко ЕГЭ 2023 математика профиль с ответами и решением
16 октября Вариант 4 Ященко ЕГЭ 2023 математика профиль с ответами и решением
23 октября Тренировочный вариант №6 ЕГЭ 2023 база по математике с ответами
24 октября Тренировочный вариант №6 ЕГЭ 2023 по математике профиль с ответами
25 октября Тренировочный вариант №7 ЕГЭ 2023 база по математике с ответами
26 октября Тренировочный вариант №7 ЕГЭ 2023 по математике профиль с ответами
28 октября Ларин вариант 403 ЕГЭ 2023 по математике профиль решение с ответами
29 октября Ларин вариант 404 ЕГЭ 2023 по математике профиль решение с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 база по математике с ответами
1 ноября 2022 Тренировочный вариант №8 решу ЕГЭ 2023 по математике профиль с ответами
5 ноября 2022 Вариант 1-2 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
6 ноября 2022 Ларин вариант 405 ЕГЭ 2023 профиль по математике решение с ответами
9 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 база по математике с ответами
12 ноября 2022 Тренировочный вариант №9 решу ЕГЭ 2023 по математике профиль с ответами
13 ноября 2022 Ларин вариант 406 ЕГЭ 2023 профиль по математике решение с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 база по математике 11 класс с ответами
15 ноября 2022 Тренировочный вариант №10 решу ЕГЭ 2023 по математике профиль с ответами
21 ноября 2022 Ларин вариант 407 ЕГЭ 2023 профиль по математике решение с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 база по математике 11 класс с ответами
23 ноября 2022 Тренировочный вариант №11 решу ЕГЭ 2023 по математике профиль с ответами
27 ноября 2022 Ларин вариант 408 ЕГЭ 2023 профиль по математике решение с ответами
28 ноября 2022 Вариант 3-4 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
30 ноября 2022 Мониторинговая работа по математике 11 класс ЕГЭ 2023 профиль 1 полугодие
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 база по математике 11 класс с ответами
3 декабря 2022 Тренировочный вариант №12 решу ЕГЭ 2023 по математике профиль с ответами
3 декабря 2022 Пробник ЕГЭ 2023 Москва по математике профиль задания и ответы
5 декабря 2022 Ларин вариант 409 ЕГЭ 2023 профиль по математике решение с ответами
9 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 база по математике 11 класс с ответами
10 декабря 2022 Тренировочный вариант №13 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
12 декабря 2022 Ларин вариант 410 ЕГЭ 2023 профиль по математике решение с ответами
13 декабря 2022 Статград математика 11 класс профиль ЕГЭ 2023 варианты МА2210209-МА2210212 и ответы
13 декабря 2022 Математика 11 класс база ЕГЭ 2023 статград варианты и ответы
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
15 декабря 2022 Тренировочный вариант №14 решу ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Вариант 5-6 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
20 декабря 2022 Ларин вариант 411 ЕГЭ 2023 профиль по математике решение с ответами
3 января 2023 Ларин вариант 412 ЕГЭ 2023 профиль по математике решение с ответами
6 января 2023 Тренировочный вариант 1-2 ЕГЭ 2023 профиль математика задания и ответы
8 января 2023 Вариант 3-4 ЕГЭ 2023 профиль математика задания и ответы
9 января 2023 Вариант 7-8 распечатай и реши ЕГЭ 2023 база по математике 11 класс с ответами
10 января 2023 Тренировочный вариант №15 и №16 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 января 2023 ЕГЭ 2023 математика тренировочные задания и ответы Ященко, Семенов
11 января 2023 Тренировочный вариант №15 и №16 база ЕГЭ 2023 по математике 11 класс с ответами
19 января 2023 Тренировочные варианты №17 и №18 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 Ларин вариант 413 и 414 ЕГЭ 2023 профиль по математике решение и ответы
22 января 2023 Тренировочный 19 вариант решу ЕГЭ 2023 профиль по математике 11 класс с ответами
22 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 19 с ответами
25 января 2023 База ЕГЭ 2023 математика 11 класс тренировочный вариант 20 с ответами
27 января 2023 Тренировочный вариант №20 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
28 января 2023 Вариант 415 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
2 февраля 2023 Вариант 21 база ЕГЭ 2023 математика 11 класс тренировочный вариант с ответами
2 февраля 2023 Тренировочный вариант №21 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
8 февраля 2023 Математика 10-11 класс ЕГЭ 2023 статград варианты база и профиль МА2200101-МА2200110 и ответы
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
11 февраля 2023 Тренировочный вариант №22 решу ЕГЭ 2023 база по математике 11 класс с ответами
12 февраля 2023 Вариант 416 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
12 февраля 2023 Вариант 417 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
13 февраля 2023 Вариант 9 и вариант 10 ЕГЭ 2023 база математика распечатай и реши задания
13 февраля 2023 Вариант 11 и вариант 12 ЕГЭ 2023 база математика распечатай и реши
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 база по математике 11 класс с ответами
16 февраля 2023 Тренировочный вариант №23 решу ЕГЭ 2023 профиль по математике 11 класс с ответами
18 февраля 2023 Вариант 418 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 база по математике 11 класс с ответами
22 февраля 2023 Пробный ЕГЭ 2023 вариант 24 профиль по математике 11 класс с ответами
25 февраля 2023 Вариант 419 Ларина ЕГЭ 2023 по математике 11 класс задания и ответы
28 февраля 2023 Статград математика 11 класс ЕГЭ 2023 база и профиль и ответы
4 марта 2023 Пробник ЕГЭ 2023 вариант 25 база по математике 11 класс с ответами
4 марта 2023 Вариант 420 Ларин ЕГЭ 2023 по математике 11 класс задания и ответы
5 марта 2023 Пробник ЕГЭ 2023 вариант 25 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 профиль по математике 11 класс с ответами
8 марта 2023 Пробник ЕГЭ 2023 вариант 26 база по математике 11 класс 100 баллов с ответами
Смотрите также на нашем сайте:
Сборник Ященко ЕГЭ 2023 математика профильный уровень 36 вариантов
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
На чтение 1 мин Просмотров 4 Опубликовано 6 марта, 2023
Решение заданий ЕГЭ профильного уровня. Задача 14 Решение и ответы на задачи на официальном сайте источника онлайн.
Презентация открытого занятия для слушателей курсов повышения квалификации. Решение задачи 14 профильного уровня ЕГЭ по математике
Варианты ответов и решение задачи — МАТЕРИАЛЫ ТУТ: https://nsportal.ru/shkola/matematika/library/2019/11/25/reshenie-zadaniy-ege-profilnogo-urovnya-zadacha-14
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
Вчера, 22:23
В закладки
Обсудить
Жалоба
Теория и практика.
Содержание
1) Прямые
2) Параболы
3) Как искать пересечение параболы и прямой, двух парабол
4) Гипербола. Асимптотические точки гиперболы
5) Пересечение гиперболы и прямой
6) Иррациональные функции
7) Пересечение корня и прямой

9) Показательные функции
10) Логарифмические функции
10_zadacha.pdf
Источник: vk.com/profimatika