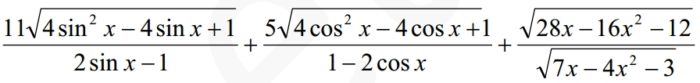Условие
2sin2x=4cosx-sinx+1 Укажите корни уравнения, принадлежащие отрезку [p/2;3p/2]
предмет не задан
41754
Решение
★
sin2x=2sinx*cosx
4sinx*cosx-4cosx+sinx-1=0
4cosx*(sinx-1)+(sinx-1)=0
(sinx-1)*(4cosx+1)=0
sinx-1=0 или 4сosx+1=0
sinx=1 или сosx=-1/4
x=(Pi/2)+2Pin, n ∈ Z или х= ± (Pi-arccos(1/4))+2Pik, k ∈ Z
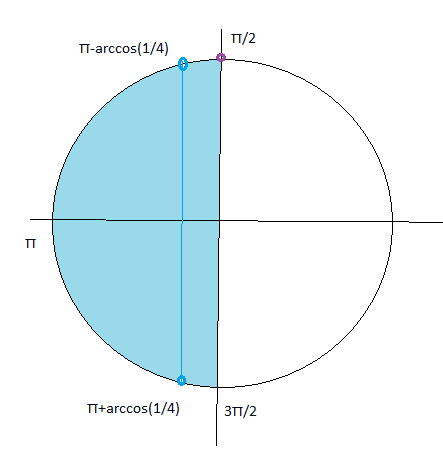
Указанному отрезку принадлежат корни ( см. рис.)
x1=(Pi/2)+2Pi*0=(Pi/2)
х2= (Pi-arccos(1/4))+2Pi*0=Pi-arccos(1/4)
х2=- (Pi-arccos(1/4))+2Pi*1=Pi+arccos(1/4)
Написать комментарий
4sinxcosx-4cosx+sinx-1=0 ⇔ 4cosx(sinx-1)+(sinx-1)=0 ⇔ (sinx-1)(4cosx+1)=0
1) sinx-1=0 2) 4cosx+1=0
sinx=1 cosx=-1/4
x=arcsin1+2πn, n∈Z x=+-arccos(-1/4)+2πn, n∈Z.
x=π/2+2πn,n∈Z. х=+-arccos1/4+2πn, n∈Z.
Отбор корней, входящих в промежуток [π/2;3π/2], этот же промежуток в градусной мере [90;270].
1) n=0
x=π/2 входит
х=+-arccos1/4 входит
2) n=1
x=π/2+2π=5π/2 не входит
х=arccos1/4+2π не входит
х=2π-arccos1/4 входит
3) n=-1
х=-3π/2 не входит
х=+-arccos-2π не входит
Ответ: х=π/2, x=+-arccos1/4, x=2π-arccos1/4.
Задания
Версия для печати и копирования в MS Word
а) Решите уравнение
б) Укажите корни, принадлежащие отрезку
Спрятать решение
Решение.
а) Сделаем замену и получим квадратное уравнение
откуда,
Уравнение
не имеет решений, а из уравнения
находим
б) Найдем корни, принадлежащие отрезку Решим неравенства:
Отрезку принадлежат корни
Ответ: a) б)
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а),
ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
|
забыли пароль? Помощь сайту |
Вопросы »Тригонометрия » решите уравнение: 2sin2x=4cosx-sinx+1 НА ОТРЕЗКЕ [П/2;3П/2] решите уравнение: 2sin2x=4cosx-sinx+1 НА ОТРЕЗКЕ [П/2;3П/2] создана: 21.04.2012 в 19:57
Diano4k : решите уравнение: 2sin2x=4cosx-sinx+1 НА ОТРЕЗКЕ [П/2; 3П/2]
Хочу написать ответ |
Найдите значение выражения:
Источник: alexlarin.net
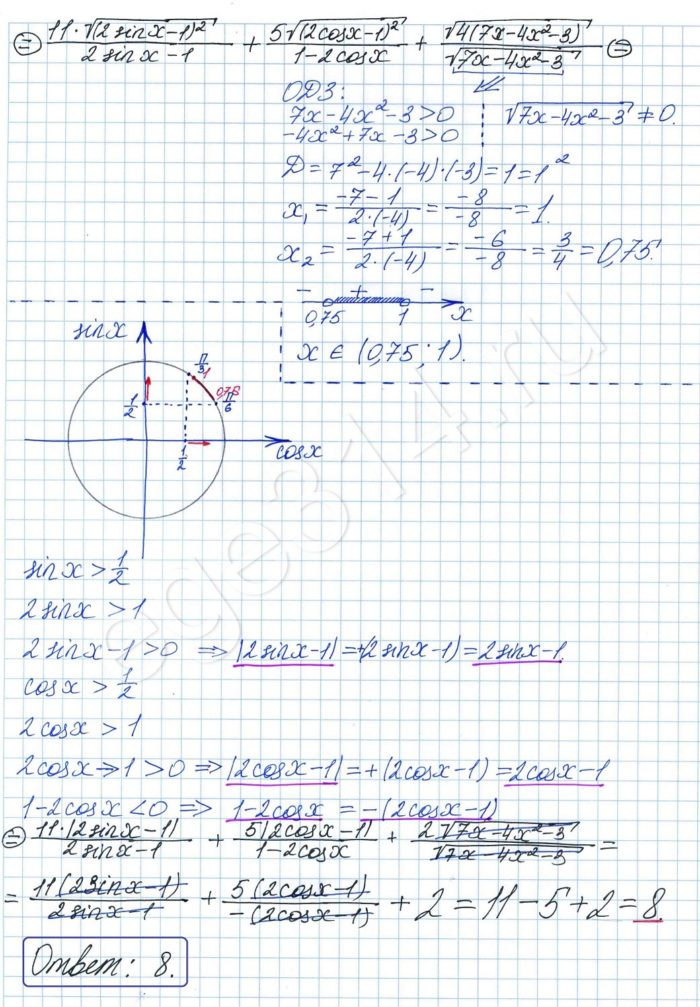
Решение:
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- Запись опубликована:05.12.2020
- Рубрика записиЗадания ЕГЭ из вариантов А. Ларина
- Автор записи:Andrei Maniakin
Калькулятор онлайн.
Решение тригонометрических уравнений.
Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение.
Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное
решение с пояснениями, т.е. отображает процесс получения ответа.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Вы можете посмотреть теорию о простейших тригонометрических уравнениях и
общие методы преобразования тригонометрических уравнениях к простейшим.
Примеры подробного решения >>
Введите тригонометрическое уравнение
Наши игры, головоломки, эмуляторы:
Немного теории.
Тригонометрические уравнения
Уравнение cos(х) = а
Из определения косинуса следует, что ( -1 leqslant cos alpha leqslant 1 ). Поэтому если |a| > 1, то уравнение cos x = a не имеет корней.
Например, уравнение cos х = -1,5 не имеет корней.
Уравнение cos x = а, где ( |a| leqslant 1 ), имеет на отрезке ( 0 leqslant x leqslant pi ) только один корень.
Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac{pi}{2} right] ); если a < 0, то в промежутке
( left( frac{pi}{2}; ; pi right] ).
Этот корень называют арккосинусом числа a и обозначают arccos a.
Определение Арккосинусом числа ( |a| leqslant 1 ) называется такое число ( 0 leqslant alpha leqslant pi ), косинус которого
равен а:
( text{arccos}(a) = alpha ) если ( cos(alpha) =a ) и ( 0 leqslant alpha leqslant pi )
Все корни уравнений вида cos(х) = а, где ( |a| leqslant 1 ), можно находить по формуле
( x = pm text{arccos}(a) +2pi n, ; n in mathbb{Z} )
Можно доказать, что для любого ( |a| leqslant 1 ) справедлива формула
( text{arccos}(-a) = pi — text{arccos}(a) )
Эта формула позволяет находить значения арккосинусов отрицательных чисел через значения арккосинусов положительных чисел.
Уравнение sin(х) = а
Из определения синуса следует, что ( -1 leqslant sin alpha leqslant 1 ). Поэтому если |a| > 1, то уравнение sin x = а не имеет корней.
Например, уравнение sin x = 2 не имеет корней.
Уравнение sin х = а, где ( |a| leqslant 1 ), на отрезке ( left[ -frac{pi}{2}; ; frac{pi}{2} right] ) имеет только один
корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac{pi}{2} right] ); если а < 0, то корень заключён
в промежутке ( left[ -frac{pi}{2}; ; 0 right) )
Этот корень называют арксинусом числа а и обозначают arcsin а
Определение Арксинусом числа ( |a| leqslant 1 ) называется такое число ( -frac{pi}{2} leqslant alpha leqslant frac{pi}{2} ),
синус которого равен а:
( text{arcsin}(a) = alpha ), если ( sin(alpha) =a ) и ( -frac{pi}{2} leqslant alpha leqslant frac{pi}{2} )
Все корни уравнений вида sin(х) = а, где ( |a| leqslant 1 ), можно находить по формуле
( x = (-1)^n text{arcsin}(a) + pi n, ; n in mathbb{Z} )
Можно доказать, что для любого ( |a| leqslant 1 ) справедлива формула
( text{arcsin}(-a) = — text{arcsin}(a) )
Эта формула позволяет находить значения арксинусов отрицательных чисел через значения арксинусов положительных чисел.
Уравнение tg(х) = а
Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет
корни при любом значении а.
Уравнение tg x = а для любого a имеет на интервале ( left( -frac{pi}{2}; ; frac{pi}{2} right) ) только один корень.
Если ( |a| geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac{pi}{2} right) ); если а < 0, то в
промежутке ( left( -frac{pi}{2}; ; 0 right) ).
Этот корень называют арктангенсом числа a и обозначают arctg a
Определение Арктангенсом любого числа a называется такое число ( -frac{pi}{2} < alpha < frac{pi}{2} ),
тангенс которого равен а:
( text{arctg}(a) = alpha ), если ( text{tg}(alpha) =a ) и ( -frac{pi}{2} < alpha < frac{pi}{2} )
Все корни уравнений вида tg(х) = а для любого a можно находить по формуле
( x = text{arctg}(a) + pi n, ; n in mathbb{Z} )
Можно доказать, что для любого a справедлива формула
( text{arctg}(-a) = — text{arctg}(a) )
Эта формула позволяет находить значения арктангенсов отрицательных чисел через значения арктангенсов положительных чисел.
Решение тригонометрических уравнений
Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а.
К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение
различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.
Уравнения, сводящиеся к квадратным
Решить уравнение 2 cos2(х) — 5 sin(х) + 1 = 0
Заменяя cos2(х) на 1 — sin2(х), получаем
2 (1 — sin2(х)) — 5 sin(х) + 1 = 0, или
2 sin2(х) + 5 sin(х) — 3 = 0.
Обозначая sin(х) = у, получаем 2у2 + 5y — 3 = 0, откуда y1 = -3, y2 = 0,5
1) sin(х) = — 3 — уравнение не имеет корней, так как |-3| > 1;
2) sin(х) = 0,5; ( x = (-1)^n text{arcsin}(0,5) + pi n = (-1)^n frac{pi}{6} + pi n, ; n in mathbb{Z} )
Ответ ( x = (-1)^n frac{pi}{6} + pi n, ; n in mathbb{Z} )
Решить уравнение 2 cos2(6х) + 8 sin(3х) cos(3x) — 4 = 0
Используя формулы
sin2(6x) + cos2(6x) = 1, sin(6х) = 2 sin(3x) cos(3x)
преобразуем уравнение:
3 (1 — sin2(6х)) + 4 sin(6х) — 4 = 0 => 3 sin2(6х) — 4 sin(6x) + 1 = 0
Обозначим sin 6x = y, получим уравнение
3y2 — 4y +1 =0, откуда y1 = 1, y2 = 1/3
1) ( sin(6x) = 1 Rightarrow 6x = frac{pi}{2} +2pi n Rightarrow x = frac{pi}{12} +frac{pi n}{3}, ; n in mathbb{Z} )
2) ( sin(6x) = frac{1}{3} Rightarrow 6x = (-1)^n text{arcsin} frac{1}{3} +pi n Rightarrow )
( Rightarrow x = frac{(-1)^n}{6} text{arcsin} frac{1}{3} +frac{pi n}{6}, ; n in mathbb{Z} )
Ответ ( x = frac{pi}{12} +frac{pi n}{3}, ;; x = frac{(-1)^n}{6} text{arcsin} frac{1}{3} +frac{pi n}{6}, ; n in mathbb{Z} )
Уравнение вида a sin(x) + b cos(x) = c
Решить уравнение 2 sin(x) + cos(x) — 2 = 0
Используя формулы ( sin(x) = 2sinfrac{x}{2} cosfrac{x}{2}, ; cos(x) = cos^2 frac{x}{2} -sin^2 frac{x}{2} )
и записывая правую часть уравпения в виде ( 2 = 2 cdot 1 = 2 left( sin^2 frac{x}{2} + cos^2 frac{x}{2} right) ) получаем
( 4sinfrac{x}{2} cosfrac{x}{2} + cos^2 frac{x}{2} — sin^2 frac{x}{2} = 2sin^2 frac{x}{2} + 2cos^2 frac{x}{2} )
( 3sin^2frac{x}{2} -4sinfrac{x}{2} cosfrac{x}{2} + cos^2 frac{x}{2} = 0 )
Поделив это уравнение на ( cos^2 frac{x}{2} ) получим равносильное уравнение
( 3 text{tg}^2frac{x}{2} — 4 text{tg}frac{x}{2} +1 = 0 )
Обозначая ( text{tg}frac{x}{2} = y ) получаем уравнение
3y2— 4y + 1 = 0, откуда y1=1, y1= 1/3
1) ( text{tg}frac{x}{2} = 1 Rightarrow frac{x}{2} = frac{pi}{4} +pi n Rightarrow x = frac{pi}{2} +2pi n, ; n in mathbb{Z} )
2) ( text{tg}frac{x}{2} = frac{1}{3} Rightarrow frac{x}{2} = text{arctg}frac{1}{3} +pi n Rightarrow x = 2 text{arctg} frac{1}{3} +2pi n, ; n in mathbb{Z} )
Ответ ( x = frac{pi}{2} +2pi n, ;; x = 2 text{arctg} frac{1}{3} +2pi n, ; n in mathbb{Z} )
В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях ( a neq 0, ; b neq 0, ; c neq 0, ; c^2 leqslant b^2+c^2 )
можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на ( sqrt{a^2+b^2} ):
( frac{a}{sqrt{a^2+b^2}} sin(x) + frac{b}{sqrt{a^2+b^2}} cos(x) = frac{c}{sqrt{a^2+b^2}} )
Введём вспомогательный аргумент ( varphi ), такой, что
( cos varphi = frac{a}{sqrt{a^2+b^2}}, ;; sin varphi = frac{b}{sqrt{a^2+b^2}} )
Такое число ( varphi ) существует, так как
( left( frac{a}{sqrt{a^2+b^2}} right)^2 + left( frac{b}{sqrt{a^2+b^2}} right)^2 = 1 )
Таким образом, уравнение можно записать в виде
( sin x cos varphi + cos x sin varphi = frac{c}{sqrt{a^2+b^2}} )
откуда
( sin(x+varphi) = frac{c}{sqrt{a^2+b^2}} )
где ( varphi = text{arccos} left( frac{a}{sqrt{a^2+b^2}} right) ) или ( varphi = text{arcsin} left( frac{b}{sqrt{a^2+b^2}} right) )
Изложенный метод преобразования уравнения вида a sin(x) + b cos(x) = c к простейшему тригонометрическому уравнению называется
методом введения вспомогательного угла.
Решить уравнение 4 sin(x) + 3 cos(x) = 5
Здесь a = 4, b = 3, ( sqrt{a^2+b^2} = 5 ). Поделим обе части уравнения на 5:
( frac{4}{5}sin(x) + frac{3}{5}cos(x) = 1 )
Введём вспомогательный аргумент ( varphi ), такой, что ( cos varphi = frac{4}{5}, ; sin varphi = frac{3}{5} )
Исходное уравнение можно записать в виде
( sin x cos varphi + cos x sin varphi = 1, ;; sin(x+varphi) = 1 )
откуда
( x+varphi = frac{pi}{2} + 2pi n, ;; varphi = text{arccos} frac{4}{5} )
( x = frac{pi}{2} — text{arccos} frac{4}{5} + 2pi n, ; n in mathbb{Z} )
Ответ ( x = frac{pi}{2} — text{arccos} frac{4}{5} + 2pi n, ; n in mathbb{Z} )
Уравнения, решаемые разложением левой части на множители
Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.
Решить уравнение sin(2х) — sin(x) = 0
Используя формулу синуса двойного аргумента, запишем уравнепие в виде 2 sin(x) cos(x) — sin(x) = 0. Вынося общий множитель
sin(x) за скобки, получаем sin(x) (2 cos x — 1) = 0
1) ( sin(x) =0, ; x = pi n, ; n in mathbb{Z} )
2) ( 2 cos(x) -1 =0, ; cos(x) = frac12, ; x = pm frac{pi}{3} +2pi n, ; n in mathbb{Z} )
Ответ ( x = pi n, ; x = pm frac{pi}{3} +2pi n, ; n in mathbb{Z} )
Решить уравнение cos(3х) cos(x) = cos(2x)
cos(2х) = cos (3х — х) = cos(3х) cos(x) + sin(3х) sin(x), поэтому уравнение примет вид sin(x) sin(3х) = 0
1) ( sin(x) =0, ; x = pi n, ; n in mathbb{Z} )
2) ( sin(3x) =0, ; x = frac{pi n}{3}, ; n in mathbb{Z} )
Заметим, что числа ( pi n ) содержатся среди чисел вида ( x = frac{pi n}{3}, ; n in mathbb{Z} )
Следовательно, первая серия корней содержится во второй.
Ответ ( x = frac{pi n}{3}, ; n in mathbb{Z} )
Решить уравнение 6 sin2(x) + 2 sin2(2x) = 5
Выразим sin2(x) через cos(2x)
Так как cos(2x) = cos2(x) — sin2(x), то
cos(2x) = 1 — sin2(x) — sin2(x), cos(2x) = 1 — 2 sin2(x), откуда
sin2(x) = 1/2 (1 — cos(2x))
Поэтому исходное уравнение можно записать так:
3(1 — cos(2x)) + 2 (1 — cos2(2х)) = 5
2 cos2(2х) + 3 cos(2х) = 0
cos(2х) (2 cos(2x) + 3) = 0
1) cos(2х) =0, ( x = frac{pi}{4} + frac{pi n}{2}, ; n in mathbb{Z} )
2) уравнение cos(2x) = -3/2 корней не имеет.
Ответ ( x = frac{pi}{4} + frac{pi n}{2}, ; n in mathbb{Z} )