В 2021 году на ЕГЭ по математике «экономические» задачи №17 оказались однотипными. Не было оптимизации. Только кредиты, причем везде – схема с дифференцированными платежами. И кажется, что уже нечего придумать по этой теме – но составители заданий ЕГЭ постарались и придумали!
Подробно о том, какими бывают «экономические» задачи на ЕГЭ, читайте здесь.
Вообще-то было понятно, что в задаче 17 должно появиться что-то новое. Не принципиально новое, конечно, а какие-то вариации на тему дифференцированных платежей.
О том, что такое схема погашения кредита с дифференцированными платежами, читайте здесь.
Мы разберем 3 задачи реального ЕГЭ-2021, а потом мою авторскую задачу, предложенную в ЕГЭ-Студии накануне экзамена на Математических тренингах. Чем-то они похожи.
1. ЕГЭ-2021
В июле 2022 года планируется взять кредит на 600 тыс. рублей. Условия его возврата таковы:
— в январе 2023. 2024 и 2025 годов долг возрастает на 20% по сравнению с концом предыдущего года:
— в январе 2026. 2027 и 2028 годов долг возрастает на r% по сравнению с концом предыдущего года;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года:
— к июлю 2028 года долг должен быть полностью погашен.
Чему равно r, если общая сумма выплат составит 984 тыс. рублей?
Решение:
Составим схему погашения кредита.
Пусть – коэффициент, показывающий, во сколько раз увеличивается сумма долга после начисления процентов в 2023, 2024 и 2025 годах,
– аналогичный коэффициент для 2026, 2027, 2028 годов.
B = 984 тыс. руб. – общая сумма выплат. Сумма долга уменьшается равномерно, т.е. на
Выплаты:
| Год | |
| 2023 | |
| 2024 | |
| 2025 | |
| 2026 | |
| 2027 | |
| 2028 |
Общая сумма выплат:
2. Вторая задача похожа на первую.
В июле 2025 года планируется взять кредит на 600 тыс. рублей. Условия его возврата таковы:
— в январе 2026, 2027, 2028, 2029 и 2030 годов долг возрастает на 13% по сравнению с концом предыдущего года;
— в январе 2031, 2032, 2033, 2034, 2035 годов долг возрастает на 12% по сравнению с концом предыдущего года;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2035 года долг должен быть полностью погашен.
Чему равна сумма всех выплат?
Решение:
тыс. рублей,
лет,
— коэффициент, показывающий, во сколько раз увеличивается сумма долга в 2026-2030 годах.
— аналогичный коэффициент для 2031-2035 годов. Долг уменьшается равномерно, т.е. ежегодно на
Составим схему погашения кредита:
Выплаты:
Общая сумма выплат:
тыс. рублей.
Ответ: 1020 тыс. рублей.
3. Третья задача похожа на «Кошмар-2018». Вы знаете, как это было в 2018 году. Все знали, что «экономическая» задача – это халява. Многие абитуриенты рассчитывали решить Часть 1 и задания 13, 15 и 17 – и получить 80 баллов, а с ними поступать куда угодно. Это было бы удобно: без изучения планиметрии и стереометрии, без «параметров» и задач на числа и их свойства – в общем, почти без усилий.
И вот на экзамене – вместо элементарной задачки – появилась задача такого типа. Надежды абитуриентов на легкое поступление растаяли, как лед на июньском солнце.
Подробно о «Кошмаре-2018» здесь.
К 2021 году чудовище приручили, и теперь оно не кажется страшным. Вот точно такая же задача из ЕГЭ-2021. Ну и что?
В середине января 2026 года планируется взять кредит на 1200 тыс. рублей. Условия его возврата таковы:
— Первого числа каждого месяца кредит увеличивается на 1%.
— Со 2 по 15 числа каждого месяца, на протяжении следующих 30 месяцев, долг должен уменьшаться на одну и ту же величину но сравнению с предыдущим месяцем.
— На тридцать первый месяц, перед начислением процентов, остаток кредита будет составлять 300 тысяч, после чего он погашается одним платежом.
Чему равна общая сумма выплат?
Решение:
тыс. рублей
X – величина, на которую уменьшается сумма долга с первого по 30-й месяцы.
тыс. рублей – сумма долга на 31-й месяц.
Составим схему погашения кредита.
Ежемесячные выплаты:
тыс. рублей,
тыс. рублей.
Общая сумма выплат:
Найдём
Мы нашли суммы арифметических прогрессий:
тыс. рублей
Общая сумма выплат:
тыс. рублей.
Ответ: 1429 500 рублей
А теперь – авторская задача Анны Малковой. Кто решил ее за день до ЕГЭ – тот на реальном экзамене знал, что делать.
4. В 2015 году Федор взял в кредит сумму S на 6 лет под 25% годовых, причем вначале банк начисляет проценты, затем Федор переводит в банк определенную сумму денег. По условиям кредита, в 2016, 2017, 2018 и 2019 годах после очередной выплаты сумма долга ежегодно уменьшается на 1/10 первоначальной величины, выплаты 2020 и 2021 годов равны. Всего Федор выплатил 250 тысяч рублей. Найдите S.
Решение:
Составим схему погашения кредита в 2016-2019 годах.
Первые 4 выплаты:
Сумма выплат за 4 года:
Пусть выплаты 2020 и 2021 годов равны X;
Выплаты за 2020 и 2021 годы:
Всего выплачено
тыс. рублей,
тыс. рублей.
5. (Резервный день) 15 декабря 2024 года планируется взять кредит в банке на 31 месяц. Условия его возврата таковы:
‐ 1‐го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
‐ с 2‐го по 14‐е число каждого месяца необходимо выплатить часть долга;
‐ 15‐го числа каждого месяца с 1‐го по 30‐й (с января 2025 года по июнь 2027 года включительно)
долг должен быть на одну и ту же сумму меньше долга на 15‐е число предыдущего месяца;
‐ 15 июня 2027 года долг составит 100 тысяч рублей;
‐ 15 июля 2027 года кредит должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 555 тысяч рублей?
Решение:
Обозначим S — сумму кредита, n = 31 месяц, p = 2%, x — сумма, на которую уменьшается долг с 1-го и по 30-й месяц; составим схему погашения кредита.
Общая сумма выплат B = 555 тыс. рублей.
Выплаты:
Общая сумма выплат:
Найдем сумму арифметической прогрессии.
По условию,
тысяч рублей.
А вы готовы к таким задачам? Научиться их решать можно на нашем Онлайн-курсе подготовки к ЕГЭ на 100 баллов.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «ЕГЭ-2021. Решение задачи 17» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Всё варианты 17 задания математика ЕГЭ Профиль 2021
Задания 17 ЕГЭ–2021
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
В июле 2025 года планируется взять кредит в банке на сумму 900 тысяч рублей на 10 лет. Условия его возврата таковы:
— в январе 2026, 2027, 2028, 2029 и 2030 годов долг возрастает на 12% по сравнению с концом предыдущего года;
— в январе 2031, 2032, 2033, 2034 и 2035 годов долг возрастает на 8% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2035 года кредит должен быть погашен полностью.
Найдите общую сумму выплат после полного погашения кредита.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
2
В июле 2025 года планируется взять кредит в банке на сумму 700 тысяч рублей на 10 лет. Условия его возврата таковы:
— в январе 2026, 2027, 2028, 2029 и 2030 годов долг возрастает на 19% по сравнению с концом предыдущего года;
— в январе 2031, 2032, 2033, 2034 и 2035 годов долг возрастает на 16% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2035 года кредит должен быть погашен полностью.
Найдите общую сумму выплат после полного погашения кредита.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
3
В июле 2025 года планируется взять кредит на 600 тысяч рублей. Условия его возврата таковы:
— в январе 2026, 2027 и 2028 годов долг возрастает на r% по сравнению с концом предыдущего года;
— в январе 2029, 2030 и 2031 годов долг возрастает на 15% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2031 года долг должен быть полностью погашен.
Чему равно r, если общая сумма выплат составит 930 тысяч рублей?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
4
В августе со 2 по 15-е число 2026 года планируется взять кредит на 1200 тысяч рублей. Условия его возврата таковы:
— первого числа каждого месяца долг увеличивается на 1%;
— со 2 по 15 числа каждого месяца, на протяжении следующих десяти месяцев, долг должен уменьшаться на одну и ту же величину по сравнению с предыдущим месяцем;
— на одиннадцатый месяц перед начислением процентов долг будет составлять 400 тыс. руб., после чего он погашается одним платежом.
Чему равна общая сумма выплат?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
5
15 января 2025 года планируется взять кредит в банке на сумму 900 тысяч рублей на 31 месяц. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 30-й (с февраля 2025 года по июль 2027 года включительно) долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца;
— 15 июля 2027 года долг составит 300 тысяч рублей;
— 15 августа 2027 года кредит должен быть погашен полностью.
Найдите общую сумму выплат после полного погашения кредита.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
6
В июле 2025 года планируется взять кредит на 600 тысяч рублей. Условия его возврата таковы:
— в январе 2026, 2027 и 2028 годов долг возрастает на r% по сравнению с концом предыдущего года;
— в январе 2029, 2030 и 2031 годов долг возрастает на 15% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2031 года долг должен быть полностью погашен.
Чему равно r, если общая сумма выплат составит 930 тысяч рублей?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
7
В июле 2025 года планируется взять кредит на 300 тыс. руб. Условия его возврата таковы:
— в январе 2026, 2027 и 2028 годов долг возрастает на r% по сравнению с концом предыдущего года;
— в январе 2029, 2030 и 2031 годов долг возрастает на 15% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2031 года долг должен быть полностью погашен.
Чему равно r, если общая сумма выплат составит 435 тысяч рублей?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
8
В июле 2025 года планируется взять кредит на 600 тыс. рублей. Условия его возврата таковы:
— в январе 2026, 2027, 2028, 2029 и 2030 годов долг возрастает на 13% по сравнению с концом предыдущего
года;
— в январе 2031, 2032, 2033, 2034, 2035 годов долг возрастает на 12% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2035 года долг должен быть полностью погашен.
Чему равна сумма всех выплат?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
9
15 декабря 2024 года планируется взять кредит в банке на 31 месяц. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 30-й (с января 2025 года по июнь 2027 года включительно) долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15 июня 2027 года долг составит 100 тысяч рублей;
— 15 июля 2027 года долг должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 555 тысяч рублей?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
10
15 декабря 2024 года планируется взять кредит в банке на сумму на 17 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 16-й (с января 2025 года по апрель 2026 года включительно) долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца;
— 15 апреля 2026 года долг составит 400 тысяч рублей;
— 15 мая 2026 года долг должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 1608 тысяч рублей?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
11
15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (млн рублей) | 1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,25 млн рублей.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
12
В июле 2025 года планируется взять кредит на 600 тысяч рублей. Условия его возврата таковы:
— в январе 2026, 2027, 2028, 2029 и 2030 годов долг возрастает на 20% по сравнению с концом предыдущего года;
— в январе 2031, 2032, 2033, 2034, 2035 годов долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2035 года долг должен быть полностью погашен.
Чему равна сумма всех выплат?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
- 10.10.2018
Практический сборник всех прототипов задания 17 из ЕГЭ по математике в 2021 году профильного уровня. Подробно разбираемся как решать любые задания такого типа на ЕГЭ.
- Решение других заданий ЕГЭ по математике
Каждое задание содержит решение и правильный ответ, благодаря которому вы можете проверить себя.
Обсудить решение заданий вы можете в комментариях ниже.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
В задание 17 ЕГЭ математика профильный уровень предлагается решить задачу с экономическим содержанием. Раздел содержит 36 заданий. В задачах требуется найти процентную ставку, исходную сумму кредита, суммарные выплаты по кредиту и т. п. Задачи требуют оригинального подхода и отличаются от стандартных задач на простые и сложные проценты, поскольку не предполагают постоянного начисления процентов в конце периода. В заданиях 17−24 нужно определить выпуск продукции, который обеспечит максимальную прибыль. Задания 29−36 содержат задачи на формулу суммы бесконечно убывающей геометрической прогрессии. Даны решения всех задач.
Этот документ можно скачать по ссылке
Полезная информация
Смотреть все
За это задание ты можешь получить 4 балла. На решение дается около 35 минут. Уровень сложности: высокий.
Средний процент выполнения: 4.2%
Ответом к заданию 17 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Что нужно знать, чтобы решить задание 17:
Для того, чтобы решить задачу необходимо составить математическую модель (уравнение, неравенство или функцию, которую нужно исследовать).
Для решения задач на кредиты, необходимо разобраться в основных схемах кредитования с дифференцированными и аннуитетными платежами. Часто для преобразования уравнения нужно знать формулы алгебраической и геометрической прогрессий.
В задачах на оптимизацию нужно уметь работать с функциями: брать производную, находить точки экстремумов.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
При каком значении $a$ множеством решений неравенства
${1+3^x} / {1+3^{-x}}>{3} / {|x+a|}$ является множество всех положительных чисел?
Решение
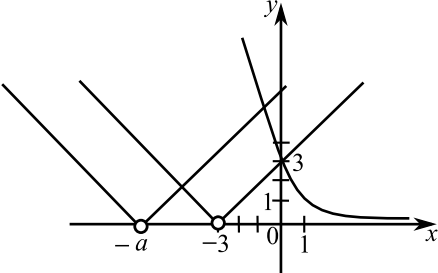
Сократив левую часть неравенства на $1 + 3^x$, получим равносильное неравенство $3^x > {3}/{|x + a|}$ или $3^{x-1} > {1}/{|x + a|}$. Так как обе части неравенства положительны, то ${1}/{3^{x-1}} < |x + a| (x ≠ -a)$ или $({1}/{3})^{x-1} < |x + a|$.
Графиком функции $y = ({1}/{3})^{x-1}$ является график функции $y = ({1}/{3})^x$ сдвинутый на $1$ единицу вправо вдоль оси $Ox$. Графиком функции $y = |x + a|$ является график функции $y = |x|$, сдвинутый вдоль оси $Ox$ в зависимости от величины и знака числа $a$. Учитывая, что $x ≠ -a$, точка $(-a; 0)$ на графиках функций $y = |x + a|$ выколота.
Множество положительных чисел будет решением этого неравенства, если точка пересечения обоих графиков лежит на оси $Oy$. Это произойдет при $a = 3$. Графическая иллюстрация приведена на рисунке.
Ответ: 3
Задача 2
При каком значении $a$ множеством решений неравенства
${1+2^{-x}} / {1+2^x}>{4} / {√ {x^2+2ax+a^2}}$ является множество всех отрицательных чисел?
Решение
Сократив левую часть неравенства на $1+2^x$ и применив свойство квадратного корня $√ {m^2}=|m|$, получим равносильное неравенство ${1} / {2^x}>{4} / {|x+a|}$ или ${1} / {2^{x+2}}>{1} / {|x+a|}$. Так как обе части неравенства положительны, то $2^{x+2}<|x+a|$, при условии $x≠ -a$. Графиком функции $y=2^{x+2}$ является график функции $y=2^x$, сдвинутый на $2$ единицы влево вдоль оси $Ox$. Графиком функции $y=|x+a|$ является график функции $y=|x|$, сдвинутый вдоль оси $Ox$ в зависимости от величины и знака числа $a$. Учитывая, что $x≠ -a$, точка $(-a;0)$ на графиках функций $y=|x+a|$ является выколотой (см. рис.). Множество отрицательных чисел будет решением неравенства, если точка пересечения обоих графиков лежит на оси $Oy$. Это произойдёт при $a=-4$. Графическая иллюстрация приведена на рисунке.
Ответ: -4
Задача 3
Найдите все значения параметра $a$, при каждом из которых система уравнений ${{table {y=a-x{,}}; {|x-2|(y+5x-10)=(x-2)^3};}$ имеет ровно четыре различных решения.
Решение
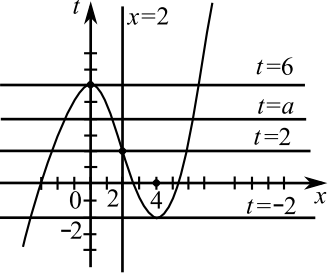
При замене $y + x = t$ получим систему уравнений ${{table t=a; {|x — 2|(t + 4x — 10) = (x — 2)^3};}$ которая имеет, столько же решений, что и заданная система.
График первого уравнения системы $t = a$ представляет собой прямую, параллельную оси абсцисс.
Построим график второго уравнения.
1) При $x ≥ 2$ получим $(x — 2)(t + 4x — 10) = (x — 2)^3$,
$(x — 2)(t + 4x — 10 — (x — 2)^2) = 0$,
$(x — 2)(t — x^2 + 8x — 14) = 0$,
$x — 2 = 0$ или $t — x^2 + 8x — 14 = 0$.
$x = 2$ — вертикальная прямая.
$t = x^2 — 8x + 14$ — парабола с вершиной $(4; -2), t(2) = 2$.
2) При $x < 2$ получим $-(x — 2)(t + 4x — 10) = (x — 2)^3$,
$(x — 2)(t + 4x — 10 + (x — 2)^2) = 0$.
$x — 2 = 0$ не выполняется при $x < 2$.
$t + 4x — 10 + (x — 2)^2 = 0, t = -x^2 + 6$ — парабола с вершиной $(0; 6), t(2) = 2$.
На рисунке изображен график второго уравнения полученной системы.
График прямой $t = a$ и уравнения $|x — 2|(t + 4x — 10) = (x — 2)^3$ имеют ровно $4$ общие точки при $-2 < a < 2, 2 < a < 6$.
Ответ: (-2;2);(2;6)
Задача 4
Найдите все значения параметра $a$, при каждом из которых уравнение ${x-4a} / {x+4}+{x-1} / {x-a}=1$ имеет единственный корень.
Решение
Преобразуем данное уравнение.
${(x — 4a)(x — a) + (x + 4)(x — 1) — (x + 4)(x — a)}/{(x + 4)(x — a)} = 0$,
${x^2 — ax — 4ax + 4a^2 + x^2 + 3x — 4 — x^2 + ax — 4x + 4a}/{(x + 4)(x — a)} = 0$,
${x^2 — x(4a + 1) + 4a^2 + 4a — 4}/{(x + 4)(x — a)} = 0$,
${tablex^2 — x(4a + 1) + 4a^2 + 4a — 4 = 0; (x + 4)(x — a) ≠ 0;$.
Решим уравнение $x^2 — x(4a + 1) + 4a^2 + 4a — 4 = 0$.
$x = {(4a + 1) ±√{-8a + 17}}/{2}$
1. При $D < 0$ уравнение корней не имеет.
2. При $D = 0, -8a + 17 = 0, a = {17}/{8}$. Уравнение имеет единственный корень $x = {4a + 1}/{2}$ при $a = {17}/{8}. x = {4 · {17}/{8} + 1}/{2} = 4.75$.
Выполнено условие $x ≠ -4, x ≠ a$.
Значит, $a = {17}/{8} = 2.125$ удовлетворяет условию задачи.
3. При $D > 0$ уравнение имеет два корня.
$x = {(4a + 1) ±√{17 — 8a}/{2}$.
Проверим при каких значениях $a$ значения $x = -4$ и $x = a$ являются корнями уравнения $x^2 — x(4a + 1) + 4a^2 + 4a — 4 = 0$.
При $x = -4$ должно выполняться равенство $16 + 4(4a + 1) + 4a^2 + 4a — 4 = 0, a^2 + 5a + 4 = 0, a = -4, a = -1$.
При $x = a$ должно выполняться равенство $a^2 — 4a^2 — a + 4a^2 + 4a — 4 = 0, a^2 + 3a — 4 = 0, a = 1, a = -4$.
При $a = -1, a = 1$ исходное уравнение имеет единственный корень.
При $а=-4$, $D>0$ и корни $х=-4$ и $х=а$ совпадают, поэтому это значение параметра также подходит
Ответ: -4$;$-1$;$1$;$2.125
Задача 5
Найдите все значения параметра $p$, при каждом из которых система неравенств ${{table {px⩾ 5,}; {p<√ {x-1},}; {3x⩾ p+2};}$ имеет хотя бы одно решение на отрезке $[4; 5]$.
Решение
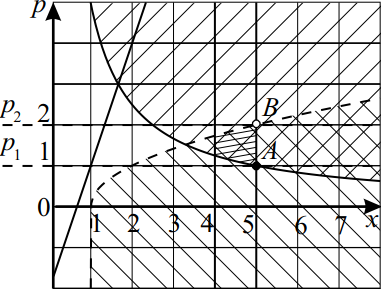
ОДЗ: $x ≥ 1$. Построим следующие графики $px = 5, p = √{x — 1}$ и $3x = p + 2$ в системе координат $Opx$ при $x > 0$ и изобразим решение системы
${tablep ≥ {5}/{x}; p < √{x — 1}; p ≤ 3x — 2;$
Из рисунка видно, что искомые значения $p$ удовлетворяют условию $p_1 ≤ p < p_2$.
Ординату точки $A$ можно найти, подставив $x = 5$ в уравнение $p = {5}/{x}; p_1 = {5}/{5} = 1$.
Ординату точки $B$ можно найти, подставив $x = 5$ в уравнение $p = √{x — 1}: p_2 = √{5 — 1} = √4 = 2$. Отсюда $p ∈ [1; 2)$.
Ответ: [1;2)
Задача 6
Найдите все целые значения параметра $a$, при каждом из которых уравнение $(ax-2x+3)(4x^6-19x^4-x^2(5+4a)-a-17)=0$ имеет хотя бы один целый корень.
Решение
Рассмотрим два случая:
1) $ax — 2x+3 = 0$; при $x = 0$ получим $3=0$, это не верно.
При $x ≠ 0, a = {2x — 3}/{x}, a = 2 — {3}/{x}$.
По условию числа $a$ и $x$ целые, поэтому число ${3}/{x}$ тоже целое, что возможно при $x = ±1, x = ±3$.
При $x = 1$ получим $a = -1$,
при $x = -1$ получим $a = 5$,
при $x = 3$ получим $a = 1$,
при $x = -3$ получим $a = 3$.
2) $4x^6 — 19x^4 — 5x^2 — 4ax^2 — a — 17 = 0$,
$a(4x^2 + 1) = 4x^6 — 19x^4 — 5x^2 — 17$,
$a = {4x^6 — 19x^4 — 5x^2 — 17}/{4x^2 + 1}$.
$a = x^4 -5x^2 — {17}/{4x^2 + 1}$. Так как $a$ и $x$ — целые числа, то ${17}/{4x^2 + 1}$ тоже целое число. Это возможно при $4x^2 + 1 = 1$ или $4x^2 + 1 = 17$.
$x^2 = 0, x = 0, a = 0 — 0 — 17 = -17$;
$x^2 = 4, x = ±2, a = 2^4 — 5·2^2 — {17}/{4·2^2 + 1} = -5$.
Уравнение имеет хотя бы один целый корень при значениях $a$, равных $-17; -5; -1; 1; 3; 5$.
Ответ:
Задача 7
Найдите все целые значения параметра $a$, при каждом из которых уравнение $(ax-2-x)(3x^5+7x^3+2x+4-3x^2a-a)=0$ имеет хотя бы один целый корень.
Решение
Рассмотрим два случая:
1) $ax — 2 — x = 0$; при $x ≠ 0$ получим $a = {2 + x}/{x} = 1 + {2}/{x}$.
Так как по условию $a$ и $x$ целые числа, то ${2}/{x}$ тоже целое число. Это возможно, если $x = ±1$ или $x = ±2$.
$x = 1; a — 2 — 1 = 0; a = 3;$
$x = -1; -a — 2 — (-1) = 0; a = -1;$
$x = 2; 2a — 2 — 2 = 0; a = 2;$
$x = -2; -2a — 2 — (-2); a = 0.$
Если $x = 0$, то $0 — 2 — 0 = 0$ не выполняется.
2) $3x^5 + 7x^3 + 2x + 4 — 3x^2a — a = 0,$
$a(3x^2 + 1) = 3x^5 + 7x^3 + 2x + 4,$
$a = {3x^5 + 7x^3 + 2x + 4}/{3x^2 + 1}$
$a = x^3 + 2x + {4}/{3x^2 + 1}$. Поскольку $a$ и $x$ — целые числа, то ${4}/{3x^2 + 1}$ также целое число. Это возможно, если $3x^2 + 1 = 4$, или $3x^2 + 1 = 2$, или $3x^2 + 1 = 1$.
Получаем $x^2 = 1$ или $3x^2 = 1$ или $x^2 = 0$.
Целые корни:
$x = 1$, тогда $a = 1^3 + 2·1 + {4}/{3·1^2 + 1} = 4$;
$x = -1$, тогда $a = (-1)^3 + 2·(-1) + {4}/{3·(-1)^2 + 1} = -2$;
$x = 0$, тогда $a = 0 + 0 + 4 = 4$.
Целые корни есть при значениях $a: -2; -1; 0; 2; 3; 4$.
Ответ: -2$;$-1$;$0$;$2$;$3$;$4
Задача 8
Найдите все значения $a > 0$, при каждом из которых система
${table(x — 4)^2 + (|y| — 4)^2 = 9; x^2 + (y — 4)^2 = a^2;$
имеет ровно $2$ решения.
Решение
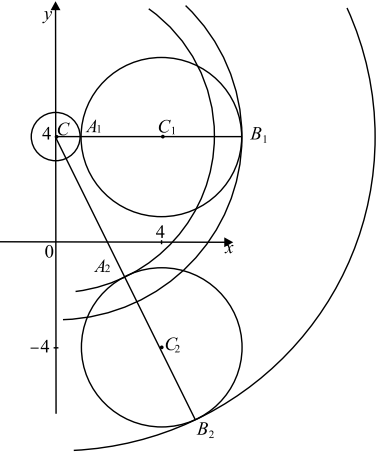
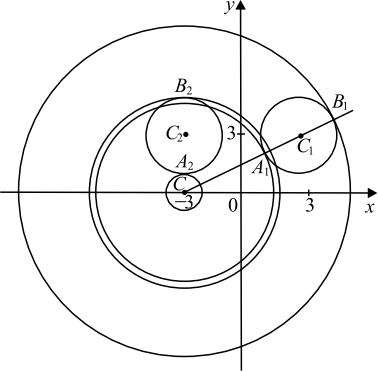
Если $y ≥ 0$, то первое уравнение задаёт окружность $∅_1$ с центром в точке $C_1(4; 4)$ радиуса $3$, а если $y < 0$, то оно задаёт окружность $∅_2$ с центром в точке $C_2(4; -4)$ того же радиуса.
При $a > 0$ второе уравнение задаёт окружность $∅$ с центром в точке $C (0; 4)$ радиуса $a$. Поэтому задача состоит в том, чтобы найти все значения параметра $a$, при каждом из которых окружность $∅$ имеет ровно две общие точки с объединением окружностей $∅_1$ и $∅_2$.
Координаты точки касания окружностей $∅$ и $∅_2$ явно видны на чертеже: это точки $A_1(1; 4)$ и $B_1(7; 4)$. То есть при $a = CA_1=1$ и $a = CB_1=7$ окружности $∅$ и $∅_2$ касаются. При $a > 7$ и $a < 1$ окружности $∅$ и $∅_1$ не пересекаются, при $1 < a < 7$ окружности $∅$ и $∅_2$ имеют $2$ общие точки.
Из точки $C$ проведём луч $CC_2$ и обозначим $A_2$ и $B_2$ точки его пересечения с окружностью $∅_2$, где $A_2$ лежит между $C$ и $C_2$. Заметим, что длина отрезка $CC_2 = √{4^2 + (4-(-4))^2} = √{80} = 4√5$.
При $a < CA_2$ или $a > CB_2$ окружности $∅$ и $∅_2$ не пересекаются. При $CA_2 < a < CB_2$ окружности $∅$ и $∅_2$ имеют $2$ общие точки. При $a = CA_2 = 4√5 − 3$ или $a = CB_2 = 4√5 + 3$, окружности $∅$ и $∅_2$ касаются.
Исходная система имеет ровно 2 решения тогда и только тогда, когда окружность $∅$ с одной из окружностей $∅_1$ и $∅_2$ имеет $2$ общие точки, а с другой не пересекается, либо касается одновременно двух окружностей.
Так как $1 < 4√5 − 3 < 7 < 4√5 + 3$, то условию задачи удовлетворяют значения $a ∈ (1; 4√5 − 3) ∪ (7; 4√5 + 3).$.
Ответ: $(1;4√5-3)∪(7;4√5+3)$
Задача 9
Найдите все значения $a > 0$, при каждом из которых система
${table(|x| — 3)^2 + (y — 3)^2 = 4; (x + 3)^2 + y^2 = a^2;$
имеет единственное решение.
Решение
Если $x ≥ 0$, то первое уравнение задаёт окружность $∅_1$ с центром в точке $C_1(3; 3)$ радиуса $2$, а если $x < 0$, то оно задаёт окружность $∅_2$ с центром в точке $C_2(−3; 3)$ того же радиуса.
При $a > 0$ второе уравнение задаёт окружность $∅$ с центром в точке $C (−3; 0)$ радиуса $a$. Поэтому задача состоит в том, чтобы найти все значения параметра $a$, при каждом из которых окружность $∅$ имеет единственную общую точку с объединением окружностей $∅_1$ и $∅_2$.
Из точки $C$ проведём луч $CC_1$ и обозначим $A_1$ и $B_1$ точки его пересечения с окружностью $∅_1$, где $A_1$ лежит между $C$ и $C_1$.
Так как $CC_1 = √{6^2 + 3^2} = √{45} = 3√5$, то $CA_1 = 3√5 − 2, CB_1 = 3√5 + 2$.
При $a < CA_1$ или $a > CB_1$ окружности $∅$ и $∅_1$ не пересекаются. При $CA_1 < a < CB_1$ окружности $∅$ и $∅_1$ имеют $2$ общие точки. При $a = CA_1 = 3√5 − 2$ или $a = CB_1 = 3√5 + 2$, окружности $∅$ и $∅_1$ касаются.
Координаты точки касания окружностей $∅$ и $∅_2$ явно видны на чертеже: это точки $A_2(−3; 1)$ и $B_2(−3; 5)$. То есть при $a = 1$ и $a = 5$ окружности $∅$ и $∅_2$ касаются. При остальных значениях параметра $a$ окружности $∅$ и $∅_2$ либо имеют $2$ общие точки, либо не имеют общих точек.
Исходная система имеет единственное решение тогда и только тогда, когда окружность $∅$ касается ровно одной из двух окружностей $∅_1$ и $∅_2$ и не пересекается с другой.
Так как $1 < 3√5 − 2 < 5 < 3√5 + 2$, то условию задачи удовлетворяют только числа $a = 1$ и $a = 3√5 + 2$.
Ответ: $1;3√5+2$
Задача 10
Найдите все значения параметра $a$, при каждом из которых решение неравенства ${(2√x — a)(a — x)}/ {√{3 — a^2 — x^2}}≥ 0$ содержит отрезок длины не менее $0.5$.
Решение
${(2√x — a)(a — x)}/{√{3 — a^2 — x^2}} ≥ 0$. Попробуем преобразовать неравенство к более простому виду. Заметим, что знаменатель влияет только на ОДЗ. Поэтому неравенство равносильно системе ${table (2√x — a)(a — x) ≥ 0; 3 — a^2 — x^2 > 0;$. Второе неравенство системы преобразуем так, чтобы получить неравенство для внутренней части круга. Первое неравенство преобразуем так, чтобы скобки выглядели симметрично ${table (2√x — a)(a — x) ≤ 0; a^2+x^2 < 3;$
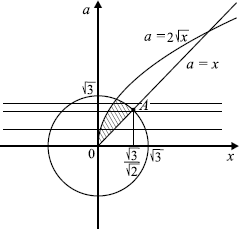
Изобразим множество решений системы в системе координат $Oxa$. Решению соответствует заштрихованная область. При этом каждому фиксированному значению $a$ соответствует горизонтальная прямая. При фиксированном значении a решениями системы будут $x$, равные абсциссам тех точек горизонтальной прямой, которые лежат в заштрихованной области.
Прямая $a = x$ пересекает окружность $x^2 + a^2 = 3$ при $a = x = {√3}/{√2}$.
1) Из рисунка видно, что если горизонтальная прямая $a = a_0$ лежит ниже (не выше) точки $A$, то отрезок этой прямой в заштрихованной области идёт от графика $a = 2√x$ до графика $a = x$.
2) Если же горизонтальная прямая $a = a_0$ лежит выше точки $A$, то отрезок этой прямой в заштрихованной области идёт от графика $a = 2√x$ до окружности $a^2 + x^2 = 3$, при этом точки самой окружности в заштрихованную область не входят.
Таким образом, в первом случае (то есть при $a ≤ {√3}/{√2}$) выполняется $a ≤ 2√x, a ≥ x$, следовательно, $x ∈ [{a^2}/{4}; a]$.
При $a > {√3}/{√2}$ решением является промежуток $[{a^2}/{4}; √{3 — a^2})$.
Отсюда решение содержит отрезок длиной не менее ${1}/{2}$, если
$[table{{table a ≤ {√3}/{√2}; a-{1}/{4}a^2 ≥ 0.5}; {{table a > {√3}/{√2}; √{3-a^2}-{a^2}/{4} > 0.5};$
$[table{{table a ≤ {√3}/{√2}; a^2-4a+2 ≤ 0}; {{table a > {√3}/{√2}; 3-a^2 > ({a^2}/{4}+{1}/{2})^2};$
Решив системы, получим: $a ∈[2-√2; {√3}/{√2}]$ или $a ∈ ({√3}/{√2}; √2)$, отсюда $a ∈ [2 — √2; √2)$.
Замечание. Задачу можно решить и другими способами, например аналитически. Получив систему, можно заметить, что первое неравенство системы при $a < 0$ не имеет решений, а при $a ≥ 0$ имеет решением промежуток $[{1}/{4}a^2; a]$ (если $a ≤ 4$) или промежуток $[a; {1}/{4}a^2]$ (если $a > 4$). Решением второго неравенства будут $x$, удовлетворяющие неравенству $x < √{3 — a^2}$. Отсюда, в частности, $a ≤ √3$, то есть случай $a > 4$ не возможен.
Несложно убедиться, что при ограничениях $0 ≤ a ≤ √3$ для решения задачи достаточно решить систему ${table a-{1}/{4}a^2 ≥ 0.5; √{3-a^2}-{a^2}/{4} > 0.5;$
Ответ: $[2-√2;√2)$
Задача 11
Найдите все значения параметра a, при каждом из которых система уравнений ${tabley=√{-8-6x-x^2}; y+ax=a+1;$ имеет единственное решение.
Решение
Построим график уравнения $y = √{−8−6x−x^2}$.
Преобразовав подкоренное выражение, получим: $y = √{1−(x^2 + 6x + 9)}, y =√{1−(x + 3)^2}$.
Если $y ≥ 0$, то $y^2 = 1−(x + 3)^2, (x + 3)^2 + y^2 = 1$.
Если $y < 0$, точек, удовлетворяющих уравнению, нет.
Получилась полуокружность радиусом $1$ с центром в точке $(−3;0)$, лежащая в верхней полуплоскости.
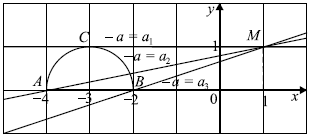
Уравнение $y + ax = a + 1$ запишем в виде $y = −a(x−1) + 1$ — семейство прямых с угловым коэффициентом $−a$, проходящих через точку $M(1;1)$.
Рассмотрим рисунок. Видно, что система имеет единственное решение, если:
1) прямая $MC$ касается полуокружности, поэтому $−a = a_1 = 0$,
2) прямая и полуокружность имеют единственную общую точку, при этом $a_2 < −a ≤ a_3$.
Найдём $a_2$ из условия, что прямая $y = a_2(x−1) + 1$ проходит через точку $A(−4;0)$.
$a_2(−4−1) + 1 = 0, a_2 ={1}/{5}$.
Найдём $a_3$ из условия, что прямая $y = a_3(x−1) + 1$ проходит через точку $B(−2;0)$.
$a_3(−2−1) + 1 = 0, a_3 ={1}/{3}$.
Имеем ${1}/{5} < −a ≤ {1}/{3}$, значит, $−{1}/{3} ≤ a < −{1}/{5}$.
Следовательно, система имеет единственное решение, если $−{1}/{3} ≤ a < −{1}/{5}$ и $a = 0$.
Ответ: $[-{1}/{3};-{1}/{5});0$
Задача 12
Найдите все значения $a$, при которых система уравнений
${tabley=√{-5-6x-x^2}; y-ax=2-3a;$
имеет ровно два решения.
Решение
Построим график уравнения $y = √{-5 — 6x — x^2}$,
Преобразовав подкоренное выражение, получим $y = √{4 — (x^2 + 6x + 9)}, y = √{2^2 — (x + 3)^2}$.
Если $y ≥ 0$, то $y^2 = 2^2 — (x + 3)^2, (x + 3)^2 + y^2 = 2^2$.
Если $y < 0$, точек, удовлетворяющих уравнению, нет.
Получилась полуокружность с центром в точке $(-3; 0)$ радиусом $2$, лежащая в верхней полуплоскости.
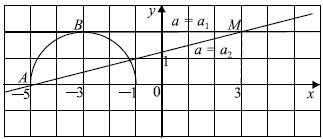
Уравнение $y-ax = 2-3a$ запишем в виде $y = a(x-3)+2$ — семейство прямых с угловым коэффициентом $a$, проходящих через точку $M (3; 2)$.
Рассмотрим рисунок. Видно, что прямая и полуокружность имеют две общие точки, если $a_1 < a ≤ a_2$. Прямая $BM$ касается окружности и является горизонтальной, поэтому её угловой коэффициент равен $0$, значит, $a_1 = 0$. Найдём $a_2$ из условия, что прямая $AM$ $y = a(x — 3) + 2$ проходит через точку $A(-5; 0)$.
$a(-5 — 3) + 2 = 0, a = {1}/{4}$, значит, $a_2 = {1}/{4}$.
Следовательно, система имеет ровно два решения при $0 < a ≤ {1}/{4}$.
Ответ: $(0;{1}/{4}]$
Задача 13
Найдите все значения $a$, при которых система уравнений
${table(x+1)^2=(y-2)^2; (x+1)^2+(y-a)^2=3a^2-2a+4;$
имеет ровно три решения.
Решение
Уравнение $(x + 1)^2 = (y — 2)^2$ равносильно совокупности двух уравнений
$[table x+1=y-2; x+1=-y+2;$ $[table y=x+3; y=-x+1;$
Множество решений этой совокупности совпадает с множеством всех точек, лежащих на двух прямых: $y = x + 3$ и $y = -x + 1$. Заметим, что эти прямые проходят через точку $(-1; 2)$, так как система ${table y = x + 3; y = -x + 1;$ имеет единственное решение $(-1; 2)$.
При каждом значении $a$ множеством решений второго уравнения системы $(x +1)^2 + (y — a)^2 = 3a^2 — 2a + 4$ будет множество всех точек окружности с центром в точке $(-1; a)$, лежащей на прямой $x = -1$, и радиусом $√{3a^2 — 2a + 4}$ (заметим, что $3a^2 — 2a + 4 > 0$ для любого $a$).
Указанные окружности будут иметь ровно три общие точки с парой указанных выше пересекающихся прямых в том и только том случае, когда окружность проходит через точку пересечения этих прямых.
В таком случае точка $(-1; 2)$ лежит на окружности, значит, верно равенство $(-1 + 1)^2 + (2 — a)^2 = 3a^2 — 2a + 4$.
Отсюда получаем: $4 — 4a + a^2 = 3a^2 — 2a + 4; 2a^2 + 2a = 0; 2a ·(a + 1) = 0; $
$a = 0$ или $a = -1$.
Ответ:
Задача 14
Найдите все значения $a$, при которых система уравнений
${table(x-3)^2=(y-1)^2; (x-a)^2+(y-1)^2=3a^2-8a+9;$
имеет ровно три решения.
Решение
Уравнение $(x — 3)^2 = (y — 1)^2$ равносильно совокупности двух уравнений
$[table x-3=y-1; x-3=-y+1;$ $[table y=x-2; y=-x+4;$
Множество решений этой совокупности совпадает с множеством всех точек, лежащих на двух прямых: $y = x — 2$ и $y = -x + 4$. Заметим, что эти прямые проходят через точку $(3; 1)$, так как система ${table y = x — 2; y = -x + 4;$ имеет единственное решение $(3; 1)$.
При каждом значении $a$ множеством решений второго уравнения системы $(x — a)^2 + (y — 1)^2 = 3a^2 — 8a + 9$ будет множество всех точек окружности с центром в точке $(a; 1)$, лежащей на прямой $y = 1$, и радиусом $√{3a^2 — 8a + 9}$ (заметим, что $3a^2 — 8a + 9 > 0$ для любого $a$).
Указанные окружности будут иметь ровно три общие точки с парой указанных выше пересекающихся прямых в том и только том случае, когда окружность проходит через точку пересечения этих прямых.
В таком случае точка $(3; 1)$ лежит на окружности, значит, верно равенство $(3 — a)^2 + (1 — 1)^2 = 3a^2 — 8a + 9$.
Отсюда получаем: $9 — 6a + a^2 = 3a^2 — 8a + 9; 2a^2 — 2a = 0; 2a ·(a — 1) = 0; a = 0$ или $a = 1$.
Ответ: $0;1$
Задача 15
Найдите все значения $a$, при каждом из которых уравнение ${3x + a — x^2 + 4a^2x — x^3}/{4a^2x — x^3} = 1$ имеет единственный корень.
Решение
В левой части уравнения выделим целую часть
${3x + a — x^2 + 4a^{2}x — x^3}/{4a^{2}x — x^3} = {4a^{2}x — x^3}/{4a^{2}x — x^3} + {-x^2 + 3x + a}/{4a^{2}x — x^3} = 1 + {-x^2 + 3x + a}/{4a^{2}x — x^3}$.
Тогда уравнение примет вид ${-x^2 + 3x + a}/{4a^{2}x — x^3} = 0$. Оно равносильно системе
${table -x^2 + 3x + a = 0; 4a^{2}x — x^3 ≠ 0;$ ${table a = x^2 — 3x; x ≠ 0, x ≠ ±2a;$
Решим систему графически в системе координат $xOa$. Для этого строим графики функций $a = x^2 — 3x$ и $a = ±{x}/{2}$.
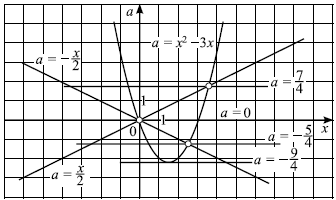
Графиком функции $a = x^2 — 3x$ является парабола, ветви которой направлены вверх. Вершина параболы — точка $({3}/{2}; -{9}/{4})$, точки $(0; 0)$ и $(3; 0)$ принадлежат параболе. Графиками функций $a = ±{x}/{2}$ являются прямые.
Решая уравнение $x^2 — 3x = {x}/{2}$, находим точки пересечения прямой $a = {x}/{2}$ и параболы $a = x^2 — 3x: x = 0, x = {7}/{2}$, откуда $a = 0, a = {7}/{4}$. Аналогично, решая уравнение $x^2 — 3x = — {x}/{2}$, находим $x = 0, x = {5}/{2}$. Тогда $a = 0, a = — {5}/{4}$. Выкалываем эти точки.
По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых при $a = — {9}/{4}, a = — {5}/{4}, a = 0, a = {7}/{4}$.
Ответ: $-{9}/{4};-{5}/{4};0;{7}/{4}$
Задача 16
Найдите все значения $a$, при каждом из которых уравнение ${x^3 + x^2 — 16a^2x — 5x + a}/{x^3 — 16a^2x}= 1$ имеет единственный корень.
Решение
В левой части уравнения выделим целую часть
${x^3 + x^2 — 16a^2x — 5x + a}/{x^3 — 16a^2x} = {x^3 — 16a^2x}/{x^3 — 16a^2x} + {x^2 — 5x + a}/{x^3 — 16a^2x} = 1 + {x^2 — 5x + a}/{x^3 — 16a^2x}$.
Тогда уравнение примет вид ${x^2 — 5x + a}/{x^3 — 16a^2x} = 0$.
Оно равносильно системе
${tablex^2 — 5x + a = 0; x^3 — 16a^2x ≠ 0;$ ${tablea = -x^2 + 5x; x ≠ 0, x ≠±4a;$
Решим систему графически в системе координат $xOa$. Для этого построим графики функций $a = -x^2 + 5x$ и $a =±{x}/{4}$.
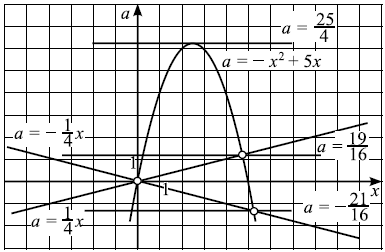
Графиком функции $a = -x^2+5x$ является парабола, ветви которой направлены вниз. Вершина параболы — точка $({5}/{2}; {25}/{4})$, точки (0; 0) и (5; 0) принадлежат параболе. Графиками функций $a =±{x}/{4}$ являются прямые.
Решая уравнение $-x^2 + 5x = {x}/{4}$, находим точки пересечения прямой $a ={x}/{4}$ и параболы $a = -x^2 + 5x: x = 0, x = {19}/{4}$, откуда $a = 0, a = {19}/{16}$. Аналогично, решая уравнение $-x^2 + 5x = -{x}/{4}$, находим $a = 0, a = -{21}/{16}$. Выкалываем эти точки.
По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых будет при $a = -{21}/{16}, a = 0, a = {19}/{16}; a = {25}/{4}$.
Ответ: $-{21}/{16};0;{19}/{16};{25}/{4}$
Задача 17
Найдите все значения параметра $а$, при которых уравнение $√{3^x-a}+{a-1}/{√{3^x-a}}=1$ имеет ровно два различных корня.
Решение
После приведения к общему знаменателю уравнение примет вид ${3x — a + a — 1}/{√{3^x — a}} = 1$ или ${3^x — 1}/{√{3^x — a}} = 1$. Пусть $3^x = t, t > 0$. Заметим, что после замены каждому положительному корню уравнения ${t — 1}/{√{t — a}} = 1$ соответствует единственный корень исходного уравнения (это следует из монотонности функции $3^x = t$). Уравнение ${t — 1}/{√{t — a}} = 1$ равносильно системе
${tablet — 1=√{t — a}; t>a;$
Возведём в квадрат обе части первого уравнения, учитывая, что $t ≥ 1$.
${tablea=-t^2+3t-1; t>a; t ≥ 1;$
Решим систему графически в системе координат $tOa$.
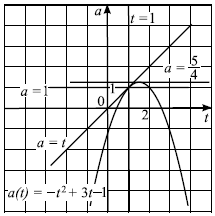
Вершина параболы $a = -t^2 + 3t — 1$ — точка с координатами $({3}/{2};{5}/{4})$.
Графики функций $a = -t^2 + 3t — 1$ и $a = t$ имеют единственную общую точку $t = 1$. Множество точек, удовлетворяющих неравенству $a < t$, представляет собой полуплоскость, лежащую ниже прямой $a = t$. $-t^2 + 3t — 1 = t, t^2 — 2t + 1 = 0, t = 1$.
По графику видно, что парабола $a = -t^2 +3t-1$ и прямая $a = const$ имеют ровно две общие точки при условии $t ≥ 1$, если $1 < a < {5}/{4}$, значит, исходное уравнение имеет ровно два корня при этих же значениях $a$.
Ответ: $(1;{5}/{4})$
Задача 18
Найдите все значения параметра $a$, при каждом из которых уравнение ${x^2+ax+2}/{2}=√{4x^2+ax+1}$ имеет ровно три различных корня.
Решение
Уравнение ${x^2 + ax + 2}/{2} = √{4x^2 + ax + 1}$ при ${x^2 + ax + 2}/{2} < 0$ не имеет корней. При $x^2 + ax + 2 ≥ 0$ обе части уравнения можно возвести в квадрат.
$(x^2 + ax + 2)^2 = 4(4x^2 + ax + 1)$,
$x^4 + ax^3 + 2x^2 + ax^3 + a^2x^2 + 2ax + 2x^2 + 2ax + 4 = 16x^2 + 4ax + 4$,
$x^4 + 2ax^3 + x^2(a^2 — 12) = 0$,
$x^2(x^2 + 2ax + a^2 — 12) = 0$,
$x^2((x + a)^2 — 12) = 0$,
$x_1 = 0, (x + a — √{12})(x + a + √{12}) = 0$,
$x_2 = -a + √{12}, x_3 = -a — √{12}$.
Чтобы исходное уравнение имело три различных корня, необходимо, чтобы числа $x_1, x_2, x_3$ были различными и для каждого из этих чисел выполнялось условие $x^2+ax+2 ≥ 0$.
$x_2≠0$ и $x_3≠0$, если $a≠√{12}=2√3$ и $a≠-√{12} = -2√3$.
Обозначим $g(x) = x^2 + ax + 2. g(0) = 2 > 0$. Числа $x_2 = -a + 2√3$ и $x_3 = -a — 2√3$ будут корнями исходного уравнения, если выполняются условия:
${tableg(x_2) ≥ 0; g(x_3) ≥ 0;$ ${table(-a + 2√3)^2 + a(-a + 2√3) + 2 ≥ 0; (-a — 2√3)^2 + a(-a — 2√3) + 2 ≥ 0;$
${table-2a√3 + 14 ≥ 0; 2a√3 + 14 ≥ 0;$ ${tablea≤{7}/{√3}; a≥-{7}/{√3};$
Таким образом, $a∊[-{7}/{√3};-2√3)∪(-2√3;2√3)∪(2√3;{7}/{√3}]$.
Ответ: $[-{7}/{√3};-2√3)∪(-2√3;2√3)∪(2√3;{7}/{√3}]$
Задача 19
Найдите все значения параметра a, при каждом из которых уравнение $x^2 + ax + 4 = √{20x^2 + 8ax + 16}$ имеет ровно три различных корня.
Решение
Уравнение $x^2 + ax + 4 = √{20x^2 + 8ax + 16}$ при $x^2 + ax + 4 <0$ не имеет корней. При $x^2+ax+4≥0$ (1) можно обе части уравнения возвести в квадрат.
$(x^2 + ax + 4)^2 = 20x^2 + 8ax + 16$,
$x^4 +ax^3+4x^2+ax^3+a^2x^2 +4ax+4x^2+4ax+16 = 20x^2+8ax+16$,
$x^4 + 2ax^3 + x^2(a^2 — 12) = 0$,
$x^2(x^2 + 2ax + a^2 — 12) = 0$,
$x^2((x + a)^2 — 12) = 0$,
$x_1 = 0, (x + a — √{12})(x + a + √{12}) = 0$,
$x_2 = -a + √{12}, x_3 = -a — √{12}$.
Чтобы исходное уравнение имело три различных корня, необходимо выполнение условия (1) для чисел $x_1, x_2, x_3$ и выполнение условия, что эти числа различны.
$x_2≠ 0$ и $x_3≠0$, если $a ≠√{12} = 2√3$ и $a ≠-√{12} = -2√3$.
Обозначим $g(x) = x^2 + ax + 4. g(x_1) = g(0) = 4 > 0$. Числа $x_2 = -a + √{12}$ и $x_3 = -a — √{12}$ будут корнями исходного уравнения, если выполняются условия:
${tableg(x_2) ≥ 0; g(x_3) ≥ 0;$ ${table(-a + √{12})^2 + a(-a + √{12}) + 4 ≥ 0; (-a — √{12})^2 + a(-a — √{12}) + 4 ≥ 0;$
${table-a√{12}+16 ≥ 0; a√{12}+16 ≥ 0;$ ${tablea≤{8}/{√3}; a≥-{8}/{√3};$
Таким образом, $a∈[-{8}/{√3}; -2√3)∪(-2√3;2√3)∪(2√3;{8}/{√3}]$
Ответ: $[-{8}/{√3};-2√3)∪(-2√3;2√3)∪(2√3;{8}/{√3}]$
Задача 20
Найдите все значения $a$, при каждом из которых система уравнений ${table(xy^2-5xy-5y+25)/{√{x+5}}=0; y=ax;$ имеет ровно два различных решения.
Решение
Решим задачу графически. Построим графики первого и второго уравнения и определим, сколько точек пересечения они имеют при различных значениях параметра.
Первое уравнение ${xy^2 — 5xy — 5y + 25}/{√{x + 5}}= 0$ параметра не содержит и представляет собой равенство дроби нулю. Это выполняется, если числитель равен нулю, а знаменатель не равен нулю, при этом оба выражения имеют смысл.
Запишем уравнение в виде ${(y — 5)(xy — 5)}/{√{x + 5}} = 0$, разложив числитель на множители.
При $x ≤ -5$ первое уравнение системы не имеет смысла. При $x > -5$ уравнение задаёт прямую $y = 5$ и гиперболу $y ={5}/{x}$.
Число решений исходной системы равно числу точек пересечения прямой $y = 5$ и гиперболы $y ={5}/{x}$ с прямой $y = ax$ при условии $x>-5$.
Найдём координаты точек $A, B$ и $C$.
$B$ — точка пересечения прямой $y = 5$ и гиперболы $y ={5}/{x}$, чтобы найти её координаты, нужно решить систему уравнений ${tabley = 5; y ={5}/{x};$
Получаем $B(1; 5)$.
У точек $A$ и $C$ абсцисса равна $-5$, ординаты находим из уравнений прямой и гиперболы. $A(-5; 5)$ и $C(-5;-1)$.
При каждом значении $a$ уравнение $y = ax$ задаёт прямую с угловым коэффициентом $a$, проходящую через начало координат. Чтобы найти значение $a$, при котором такая прямая проходит через точку с указанными координатами, нужно подставить координаты в уравнение прямой.
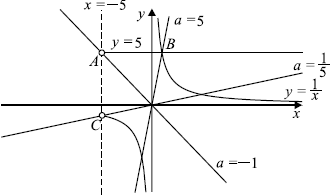
Например, для точки $A(-5; 5)$ получаем $x = -5; y = 5; 5 = a·(-5); a = -1$. Аналогично для $B(1; 5)$ получим $a = 5$. Для $C(-5;-1)$ получим $a ={1}/{5}$.
При $x>-5$ прямая $y = ax$ пересекает прямую $y = 5$ при $a<-1$ и $a>0$, пересекает правую ветвь гиперболы $y ={5}/{x}$ при $a>0$, пересекает левую ветвь гиперболы $y ={5}/{x}$ при $a>{1}/{5}$. При этом прямая $y = ax$ проходит через точку пересечения прямой $y = 5$ и гиперболы $y ={5}/{x}$ при $a = 5$.
Таким образом, исходная система имеет ровно два решения при $0< a ≤0.2; a = 5$.
Ответ: $(0;0.2]∪${5}